不同方法研究微溶剂化尿嘧啶激发能
2016-01-16崔苗苗,尹世伟
不同方法研究微溶剂化尿嘧啶激发能
崔苗苗, 尹世伟*
(大分子科学陕西省重点实验室, 陕西师范大学 化学化工学院, 陕西 西安 710119)
摘要:采用基于两体片段分子轨道法的含时密度泛函理论方法(FMO2-TDDFT)研究包含4个和13个水分子微溶剂化的尿嘧啶分子激发态能。研究表明,FMO2-TDDFT和TDDFT的计算结果基本一致;在LC-BLYP泛函下考察了两种不同方法、不同基组对计算激发能的影响。结果显示,随着基组增大,FMO2-TDDFT方法计算的第一激发能增大,第二激发态能量减小。通过两种方法比较,FMO2-TDDFT方法在处理较大体系时具有一定优势。
关键词:含时密度泛函理论(TDDFT); 尿嘧啶; 溶剂化; 片段分子轨道法(FMO)
中图分类号:O641.3文献标志码: A
文章编号:1672-4291(2015)01-0070-05
doi:10.15983/j.cnki.jsnu.2015.01.315
收稿日期:2014-06-05
基金项目:国家自然科学基金资助项目(31260059,30900105); 教育部科学技术研究重点项目(20110220); 甘肃省高校基本科研业务费项目
文章编号:1672-4291(2015)01-0065-05
doi:10.15983/j.cnki.jsnu.2015.01.314
收稿日期:2014-04-17
基金项目:国家自然科学基金面上项目(81172130)
Different approaches to study excited energy of
micro-solvent uracil molecular
CUI Miaomiao, YIN Shiwei*
(Key Laboratory for Macromolecular Science of Shaanxi Province, School of Chemistry and
Chemical Engineering, Shaanxi Normal University, Xi′an 710119, Shaanxi, China)
Abstract:Since the traditional time-dependent density functional theory (TDDFT) method can not deal with large complex system,two body fragment molecular orbital method coupled with time-dependent density functional theory (FMO2-TDDFT) method was employed to research the excited energy of uracil in water solution. The results show that the lowest excited energies S1 and S2 obtained from FMO2-TDDFT are quite well agreement with values of TDDFT calculations. The effects of the basis set on the excited energies also were investigated in these two different calculations. The results show that the S1 energies from FMO2-TDDFT and traditional TDDFT increase while S2 energy values decrease with the increasing of polar functions in basis set. In addition, the excited state structure of supermolecules around the center of uracil was calculated by FMO and TDDFT. The results show that FMO2-TDDFT has some advantages in calculating the lowest excited state in the large system.
Key words: time-dependent density functional theory(TDDFT); uracil; solvation; fragment molecular orbital method (FMO)
DNA和RNA核酸碱基分子在生物中起着保存和传递基因信息的作用[1]。核酸分子激发态性质及其动力学的光物理光化学过程研究对于理解核酸的紫外线损伤机理,预防光致基因突变具有重要意义。碱基分子是紫外线强吸收体,对其吸收和发射光谱的稳态和瞬态光谱的研究一直是该领域的研究热点和难点。20世纪70年代开始,关于溶剂理论的研究蓬勃发展,主要是根据两种不同的理论思想[2-3]。第一种是集中在有限数目的溶质和溶剂分子的微观相互作用上,在这种模型中可以逐渐增加溶剂分子的数目,所以可以获得有关溶剂效应的更详细的信息[4-5]。第二种是引进统计平均信息来考虑溶剂化场效应,即用具有某种适当性质的宏观连续介质取代明确溶剂分子的微观描述[6]。
水-尿嘧啶复合物激发态的理论研究已经开展多年。2001年,Mahio Chiba等人[7]首先采用含时密度泛函理论研究了含有7个水分子的尿嘧啶分子几何结构和分子振动模式;2006年,鲍晓光考查了1~3个水分子结合尿嘧啶中氢键的作用[8],并计算了中性和阴离子态激发态能,分析了尿嘧啶分子中的两个氧原子与水中氢原子结合形成氢键的稳定性;2007年,他们又进行了3~5个水分子对尿嘧啶激发能的影响,得出低壳层下的水分子作用的尿嘧啶的稳定性强于将水作为高壳层下的尿嘧啶分子,研究表明尿嘧啶分子与水分子结合后,氢键对激发态能量有一定的影响[9-11]。
目前含时密度泛函理论(TDDFT)方法是一种计算代价与CIS相当,计算结果明显优于CIS的高效计算方法。但传统的TDDFT方法计算量与体系电子个数成N4关系[12],因此需要寻求一种新的、可以做到线性标度Order(N)计算复杂体系激发态的方法。目前,Kitaura提出片段分子轨道方法方法[13],Chiba等人[6]在2007年实现了两体片段分子轨道法(FMO2)与含时密度泛函理论(TDDFT)的结合。
片段分子轨道方法,简称FMO,是将整个体系分为小片段,计算得到片段单体和二聚体的能量,而且基于TDDFT的FMO计算与基于从头计算方法的FMO计算结果接近。FMO方法扩展到电子的相关理论,多层FMO方法可以计算大的体系。在FMO方法中,体系被分为若干小片段。先对单体片段进行计算,密度自洽收敛后,进行两体片段的计算。总能量E是片段单体能量EI=(I=1,2,…, N;N是片段的数量)和片段二聚体能量EIJ的总和,即

(1)
Chiba等人[6]将FMO思想扩展到激发态体系中,激发态能量E*基于FMO方法得到,类似于式(1),并与溶剂化体系的偶极场方法类似。假设激发大多是局域在片段M,加上其他的片段两体校正后得到的能量,即


(2)
式中上标0和*分别表示基态和激发态。激发能量由FMO2给出:

(3)

本文从微溶剂化的角度比较研究FMO-TDDFT与全电子传统DFT计算尿嘧啶分子激发态的性质,评估测试2010年版 FMO-TDDFT的优越性[14],发现FMO能得到与传统TDDFT基本一致的计算结果,而且在计算时间上有明显的优势,可作为计算较大体系激发态的有效方法。
1计算过程
首先选取文献[15]中使用动力学优化得到的包含最邻近4个水分子超分子结构为基准,分别用两体片段分子轨道法(FMO2-TDDFT)以及含时密度泛函理论计算研究体系如图1所示。在FMO方法中(如图1a),将超分子体系划分为5个片段,用于

图1 FMO方法(a)与传统DFT方法(b)
求解尿嘧啶分子激发态,而环境四个水分子对尿嘧啶激发态的影响则是通过公式(2)两体校正的方法求得。作为比较对照,传统TDDFT方法则是将整个超分子体系作为一个整体,使用DFT放大计算整个超分子体系的激发态能量。计算均使用从头计算量子化学程序和碎片分子轨道理论(GAMESS-FMO),其可以支持长程校正泛函(LC-BLYP),另外还测试不同基组对计算结果的影响。
微溶剂计算则是采用Forcite模块进行分子动力学模拟, 运用Material Studio 5.5软件[14]的Amorphous Cell模块和Forcite模块进行分子动力学模拟:(1) 优化(Geometry Optimization)得到初始结构:用COMPASS力场作用模型,对其得到的体系用Smart Minimizer方法进行分子力场优化,它可以根据体系模型的特点自动选择最优化方法对体系进行能量优化。开始时通过最陡下降法,接着采用共轭梯度法对体系进一步优化,最后通过牛顿拉普森优化得到其优化结构,静电(Electrostatic)和范德华(van der Waals)相互作用都采用Ewald加和[16];(2) 采用NVT(正则)系综进行分子动力学模拟,温度为298 K,三维空间都采用周期性边界条件,积分步长1 fs,非键相互作用(静电和范德华)均采用Ewald,cutoff=1.5 nm,模拟盒中各原子的起始速度由Maxwell-Boltzmann分布随机指定,Nose-Anderson方法控制体系的温度,经过1 ns的分子动力学体系趋于稳定;接着再用NVT(正则)系综,温度仍为298 K,温度控制则采用Berendsen方法,非键相互作用(静电和范德华)均仍用Ewald,进行300 ps的分子动力学模拟,得到其平衡结构,取最后这300 ps平衡轨迹文件进行数据分析。每5 ps收集一个构象,随机选取一个构象进行研究。截选距离尿嘧啶分子中心不同范围内的结构, 运用两种方法进行计算研究。所有的FMO计算均使用修正后的Gamess[14]版本完成。
2结果与讨论
2.1四水结构下不同方法结果对比分析
对于选定的四水结构尿嘧啶分子(见图1),分别在GAMESS下用两体片段分子轨道法(FMO2-TDDFT)和含时间相关的密度泛函理论TDDFT下的计算,以及不同基组计算的激发态能量结果见表1。

表1 四水结构下的尿嘧啶分子不同方法激发能量 *
*Osc.代表谐振子强度,下同。
由表1可以看出,对于第一激发态(S1)和第二激发态(S2)能量而言,FMO2计算的结果要明显优于FMO1结构相比于参考态传统TDDFT计算的结果,相对偏差均小于0.1 eV ;但对于更高激发态S3而言,FMO1和FMO2相比于全电子TDDFT表现出无规律行为。例如:在6-31 g基组和6-31 g(d, p)基组计算中,FMO1计算得到的S3激发能相比于TDDFT结果呈减小趋势,而在6-311 g(2d, 2p)基组,又呈增大趋势;FMO2方法在计算S3激发能时随着选择基组极化数的增大,能量呈现很大的增长趋势,高估了FMO2方法在处理电子上的能力,所以FMO方法不适合进行高激发态的能量计算[6]。
随着选择基组极化数目增大,TDDFT计算下的S1激发能也随之增大,而在S2和S3的计算中则随着极化数目增大而减小;同样在FMO1和FMO2计算中,S1呈现出与TDDFT的S1相同的规律,即随着考虑极化数目增大而增大,S2和S3结果则随着基组极化数增多呈下降趋势。由此可以看出,同一个水平下的激发态计算中,FMO和TDDFT在处理四水结构下尿嘧啶低激发能量结果基本一致。
2.2溶剂水分子对尿嘧啶分子低激发态能量影响
根据分子动力学,NVT系热力学稳定构象。随机选取距尿嘧啶分子中心不同半径内水分子的超分子微溶剂构象来研究环境对溶质分子激发态影响。 这里分别选取0.4 nm(4水分子)和0.5 nm(13水分子)范围的微溶剂结构如图2和表2所示。

图2 距离中心尿嘧啶分子0.5 nm范围的包含
由表2可以得出,含4水的尿嘧啶分子两种方法计算结果中,FMO1的S1能量与TDDFT计算的能量差为0.026 eV,FMO2与TDDFT的S1能量差为0.005 eV;在S2能量计算中,相差的能量分别为0.166 eV、0.004 eV,可以看出FMO2的结果更接近TDDFT计算的结果。在包含了13个水分子的尿嘧啶结构中,S1对应的能量差为0.029 eV、0.010 eV;在S2计算中的能量差为0.246 eV、0.003 eV,同样是FMO2方法能更好地拟合传统的TDDFT计算结果。从计算所花费的时间可以看出,FMO方法计算所需时间少于TDDFT方法。 FMO方法在计算低激发态能量上优于TDDFT方法。
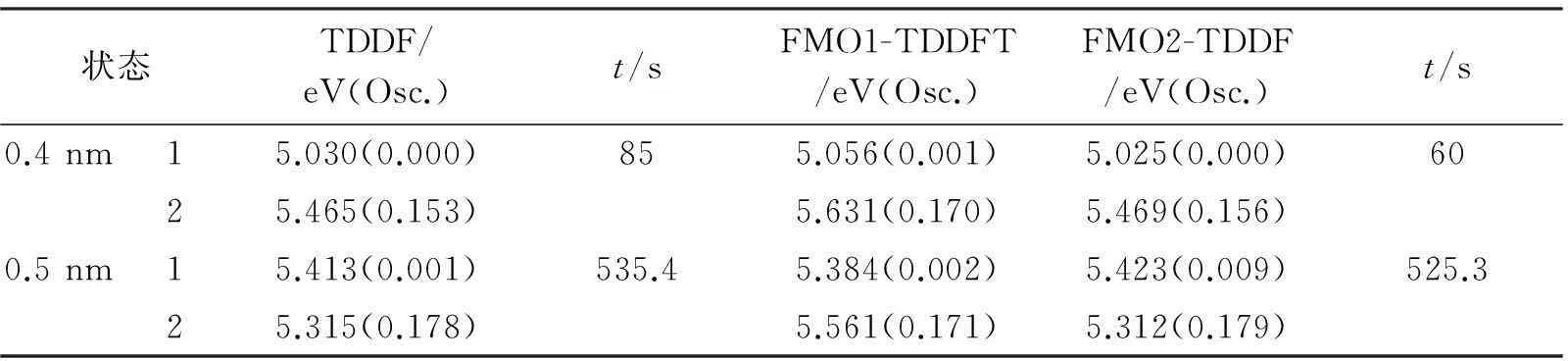
表2 微溶剂下的尿嘧啶复合物不同方法激发能
3结论
FMO-TDDFT方法虽能很好地与传统含时密度泛函理论计算结果相一致,尤其是低激发态能量,但其计算激发态容易过多校正两体效应对激发态能量影响,最终表现出非物理无规律的计算结果;随着选择基组极化函数的增大,TDDFT计算S1能量也随之增大,FMO计算S1能量也与TDDFT一致,而S2能量却表现出随着基组极化数增大而呈下降趋势。基于片段分子轨道法的含时密度泛函理论方法(FMO-TDDFT)计算微水溶剂化下的尿嘧啶分子较含时密度泛函理论方法TDDFT有一定的优势,可为大量水溶剂计算提供一定的参考价值。
参考文献:
[1] Les A, Adamowicz L, Bartlett R J. Relative stablity of cytosine tautomes with the user method and 1st-order correlation orbitals[J].Journal of Physical Chemistry, 1989, 93:400-405.
[2] Goldblum A, Perahia D, Pullman A. Hydration scheme of the complementary base-pairs of DNA[J]. FEBS Letters, 1978, 91: 213-215.
[3] Miertus S,Tomasi J.Approximate evaluations of the electrostatic free energy and internal energy changes in solution processes[J].Chemical Physics, 1982, 65: 239-245.
[4] Gaigeot Marie Pierre, Mahmoud Ghomi. Geometrical, vibrational properties of nucleic acid constituents interacting with explicit water molecules as analyzed by density functional theory calculations.1. Uracil +nwH2O(nw=1,…,7)[J]. Journal of Physical Chemistry B, 2001, 105: 5007-5017.
[5] Mahito Chiba. Excited state geometry optimizations by time-dependent density functional theory based on the fragment molecular orbital method[J]. Chemical Physics Letters, 2009, 474: 227-232.
[6] Chiba M, Fedorov D G, Kitaura K.Time-dependent density functional theory with the multilayer fragment molecular orbital method[J]. Chemical Physics Letters, 2007, 444: 346-350.
[7] Mahito Chiba. Time-dependent density functional theory based upon the fragment molecular orbital method[J]. Journal of Chemical Physics, 2007,127: 104-108.
[8] Bao Xiaoguang. Microsolvation effect, Hydrogen-Bonding pattern, and electron affinity of the uracil-water complexes U-(H2O)n(n=1, 2, 3)[J]. Journal of Physical Chemistry B, 2006, 110: 5865-5874.
[9] Bao Xiaoguang. Microsolvation pattern of the hydrated radical anion of uracil: U-(H2O)n(n=3-5)[J]. Journal of Physical Chemistry A, 2007, 111: 666-672.
[10] Laudo Mariana Di. Effects of hydrogen bonding on the acidity of uracil[J]. Journal of Physical Chemistry A, 2003, 107:10406-10413.
[11] Iwona Da Bkowska. Computational study of hydrogen-bonded complexes between the most stable tautomers of glycine and uracil[J]. Journal of Physical Chemistry A, 2002, 106: 7423-7433.
[12] Stratmann R E, Scuseria G E, Frisch M J. An efficient implementation of time-dependent density-functional theory for the calculation of excitation energies of large molecules[J]. Journal of Chemical Physics, 1998, 109: 8218-8224.
[13] Fedorov D G, Kitaura K. Extending the power of quantum chemistry to large systems with the fragment molecular orbital method[J]. Journal of Physical Chemistry A,2007, 111: 6904-6914.
[14] Accelrys Software Inc.Materials studio 5.5[M].San Diego: Accelrys Inc., 2010.
[15] Roberto Improta. Absorption and fluorescence spectra of uracil in the gas phase and in aqueous solution: A TD-DFT quantum mechanical study[J]. Journal of the American Chemical Society, 2004, 126:14320-14321.
[16] Wolf D, Keblinski P. Exact method for the simulation of coulombic systems by spherically truncated, pairwiser-1 summation[J]. Journal of Chemical Physics, 1999, 110:8254-8282.
〔责任编辑王勇〕
第一作者:冯汉青,男,副教授,博士,主要从事植物抗逆生理学研究。E-mail:fenghanq@nwnu.edu.cn
第一作者: 闫位娟,女,博士,主要研究方向为生物化学与放射肿瘤学。E-mail: missyan3611@163.com
*通信作者: 江其生,男,教授,博士生导师。E-mail:jqs598@sina.com
