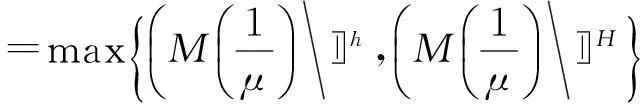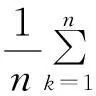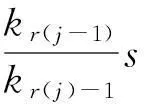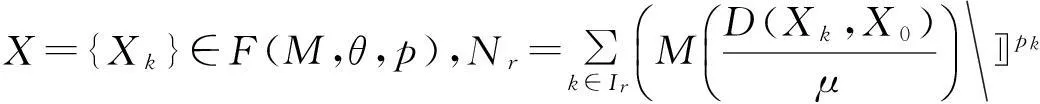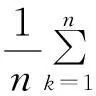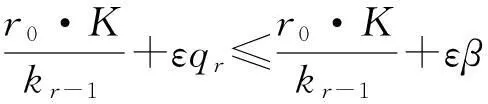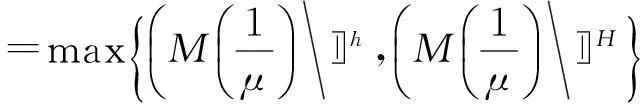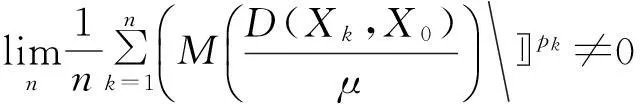基于Orlicz函数及强缺项收敛的模糊数列空间

基于Orlicz函数及强缺项收敛的模糊数列空间

巩增泰， 冯雪

(西北师范大学 数学与统计学院， 甘肃 兰州 730070)

摘要：作为缺项统计收敛模糊数列空间的推广，基于Orlicz函数，在定义模糊数列强缺项收敛的基础上，提出和讨论了三类基于Orlicz函数的模糊数列空间F(M,θ,p),F0(M,θ,p)和F∞(M,θ,p)，并证明了空间的线性性质；最后通过研究模糊数列强缺项收敛与缺项统计收敛之间、强缺项收敛与强收敛之间的相互关系，得到几类基于Orlicz函数的模糊数列空间的包含关系。

关键词:模糊数； Orlicz函数； 模糊数列空间

中图分类号：O159文献标志码： A

文章编号：1672-4291(2015)01-0008-05

doi:10.15983/j.cnki.jsnu.2015.01.112

收稿日期：2014-02-26

基金项目：国家自然科学基金资助项目(11371248); 安徽省高校自然科学

On sequence spaces of fuzzy numbers based on Orlicz functions

and strongly lacunary convergence

GONG Zengtai, FENG Xue

(College of Mathematics and Statistics, Northwest Normal University, Lanzhou 730070, Gansu, China)

Abstract:As an extension of the lacunary statistical convergent sequence space of fuzzy numbers,some sequence spaces of fuzzy numbers,F(M,θ,p),F0(M,θ,p) and F∞(M,θ,p) based on Orlicz functions and strongly lacunary convergence are defined and discussed.It is shown that the spaces are linear spaces.In addition,the relationships of them are investigated by means of the discussion of strongly lacunary convergence,lacunary statistical convergence and strong convergence for the sequence of fuzzy numbers.

Key words: fuzzy numbers; Orlicz functions; sequence spaces of fuzzy numbers

MR subject classification: 26A39, 26A42

自1951年Fast[1]引入统计收敛的概念以来，统计收敛问题得到许多学者[2-8]的深入研究。值得注意的是,自20世纪90年代以来,对统计收敛的研究异常活跃，其讨论涉及矩阵求和、级数理论、傅里叶分析、三角级数以及Banach空间理论等诸多领域。考虑具体数学建模过程中数据和信息的不确定性，而这种不确定性往往表现为一个模糊数[9-10]，所以对于模糊数列收敛问题的研究显得非常必要。2001年，Savas[11]讨论了模糊数列的统计收敛，并给出了刻画定理，结果表明收剑的模糊数列可以表示为一个普通收敛的模糊数列与一个零自然密度模糊数列的和。2006年，Aytar等人[12]提出了统计有界模糊数列的统计上、下极限定义，并得到了统计有界的模糊数列统计收敛与其统计上、下极限之间的关系。2008年，Anastassiou[13]给出了基于非负正则可和矩阵的模糊数序列的统计收敛和连续模糊数值函数模糊模的定义，证明了模糊正线性算子的Korovkin定理，并利用连续模糊估计了基于非负正则可和矩阵算子的统计收敛速率。2008年，Kumar[14]将自然密度为0的自然数子列集合看作一个理想，作为模糊数列统计收敛的推广，提出并讨论了模糊数列的理想收敛。2011年，巩增泰等[15]在引入模糊数值函数统计收敛、一致统计收敛、等度统计收敛等概念的基础上，讨论了它们之间的相互关系及其水平截函数之间的关系,并在测度有限的情况下，得到了模糊数值函数统计收敛的Egorov定理和勒贝格定理。此外，作为收敛的另一种推广，1989年，Nuray[16]就模糊数列的缺项统计收敛做了深入研究，提出并证明了模糊数列统计收敛集与缺项统计收敛集之间的关系。2001年Kwon[17]就模糊数列统计收敛集与缺项统计收敛集之间的关系做了研究。2012年，文献[18]将模糊数列的统计收敛和缺项统计收敛置于理想的框架下，研究了模糊数列的理想统计收敛、理想缺项统计收敛、缺项统计收敛之间的相互关系。关于Orlicz序列空间的研究始于1971年Lindenstrauss和Tzafriri[19]的工作，结果表明任何一个Orlicz序列空间lM包含一个同构于lp(1≤p<∞)的子空间。而后,文献[20-22]分别利用Orlicz函数定义和推广了Orlicz序列空间lM及强可和序列空间。文献[23]是国内对Orlicz空间理论较为系统的研究。作为缺项统计收敛的模糊数列空间之推广，本文基于Orlicz函数，在定义模糊数列强缺项收敛的基础上，提出和讨论三个基于Orlicz函数的模糊数列空间F(M,θ,p),F0(M,θ,p)和F∞(M,θ,p)，并证明了空间的线性性质。最后在讨论模糊数列强缺项收敛、缺项统计收敛以及强收敛相互关系的基础上，研究了所提出的模糊数列空间的包含关系，推广了前人的工作。

1定义及说明

实数R上的模糊集u称为模糊数，是指u是正规的,凸模糊集,隶属度函数u(x)上半连续,支撑集[u]0=cl{x∈R:u(x)>0}为紧集[9-10]。记所有模糊数组成的集合为E1。对任意的0≤r≤1,水平截集[u]r={x:u(x)≥r}是一个闭区间。对u、v∈E1,k∈R，加法和数乘[9]为

[u+v]r=[u]r+[v]r;[ku]r=k[u]r。

模糊数u、v∈E1之间距离为

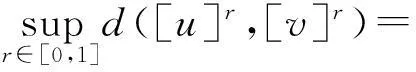
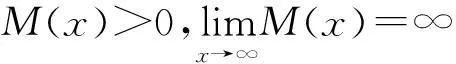
定义1设M是Orlicz函数，X={Xk}是模糊数列,θ={kr}是缺项数列,p={pk}是正实数列。对于μ>0，定义下列基于Orlicz函数和强缺项收敛的模糊数列空间:

F(M,θ,p)=

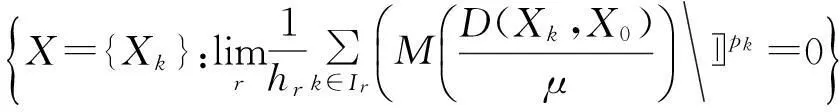
F0(M,θ,p)=

F∞(M,θ,p)=

注2当M(x)=x,θ=2r时，F(M,θ,p)=F(p),F0(M,θ,p)=F0(p),F∞(M,θ,p)=F∞(p)，其中模糊数列空间F(p)、F0(p)、F∞(p)最早是由文献[25]提出和讨论的，即

F(p)=

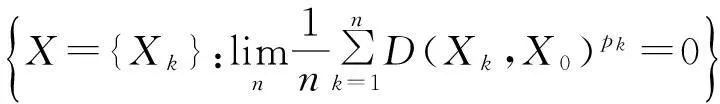
F0(p)=

F∞(p)=

注3当θ=r,pk=1,{Xk}为实数列时，F∞(M,θ,p)=lM,其中Orlicz序列空间lM最早是由文献[19]提出和讨论的。

2空间F(M,θ,p)、F0(M,θ,p)、F∞(M,θ,p)的性质和相互关系

定理1若数列p={pk}有界，则F0(M,θ,p)⊂F(M,θ,p)⊂F∞(M,θ,p)。

证明显然，F0(M,θ,p)⊂F(M,θ,p)成立。设X={Xk}∈F(M,θ,p),则

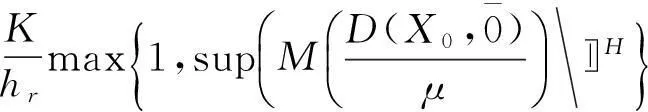
定理2空间F(M,θ,p)、F0(M,θ,p)和F∞(M,θ,p)是实数域上的线性空间。

证明仅证明F0(M,θ,p),其他类似。设X={Xk},Y={Yk}∈F0(M,θ,p)，α、β∈R。可以证明

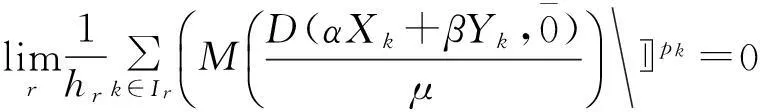
事实上，由于X={Xk},Y={Yk}∈F0(M,θ,p),所以存在μ1>0,μ2>0,使得

取μ=max(2|α|μ1,2|β|μ2)，由M是连续非降的凸函数可得

证明设X={Xk}∈F(θ,p)，即

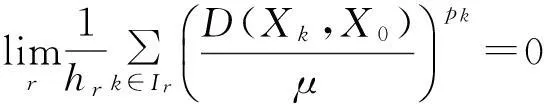
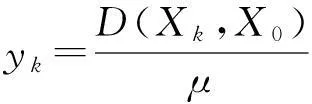
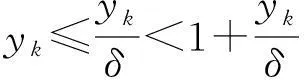
3空间F(M,θ,p)与缺项统计收敛模糊数列空间S(θ)的相互关系

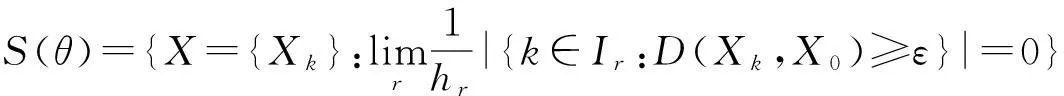
1)F(M,θ,p)⊂S(θ);

2) 如果X={Xk}∈l∞∩S(θ),那么X={Xk}∈F(M,θ,p);

3)l∞∩S(θ)=l∞∩F(M,θ,p)。

证明1) 因为X={Xk}∈F(M,θ,p),所以

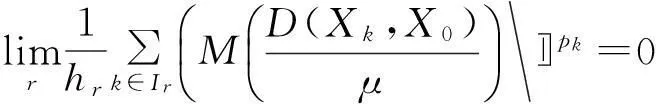
2) 因为X={Xk}∈l∞∩S(θ),所以存在常数T>0,使得D(Xk,X0)≤T。

3) 由1)、2)的证明可得。

注4如果模糊数列X={Xk}关于Orlicz函数M强缺项收敛，那么X={Xk}缺项统计收敛。

注5当模糊数列X={Xk}有界时，X={Xk}关于Orlicz函数M强缺项收敛与缺项统计收敛等价。

4基于Orlicz函数和强收敛的模糊数列空间F(M,p)、F0(M,p)、F∞(M,p)的性质及其与空间F(M,θ,p)、F(M,p)的相互关系

定义2设M是Orlicz函数，X={Xk}是模糊数列，p={pk}是正实数列。对于μ>0，定义下列基于Orlicz函数和强收敛的模糊数列空间:

F(M,p)=

F0(M,p)=

F∞(M,p)=

注7当M(x)=x时，F(M,p)=F(p),F0(M,p)=F0(p),F∞(M,p)=F∞(p)。

注8当θ=2r时，F(M,θ,p)=F(M,p),

F0(M,θ,p)=F0(M,p),

F∞(M,θ,p)=F∞(M,p)。

完全类似于定理1—4的证明，关于模糊数列X={Xk}关于Orlicz函数M强收敛有如下结果。

定理6若数列p={pk}有界，则F0(M,p)⊂F(M,p)⊂F∞(M,p)。

定理7空间F(M,p)、F0(M,p)和F∞(M,p)是实数域上的线性空间。

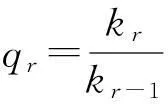
定理10设θ是缺项数列。若lim infrqr>1,则F(M,p)⊂F(M,θ,p)。当lim infrqr=1时，结论不一定成立。

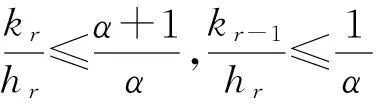
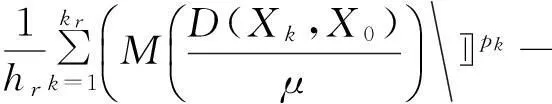
因为X={Xk}∈F(M,p)，即

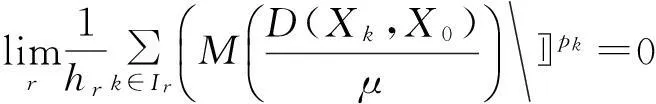
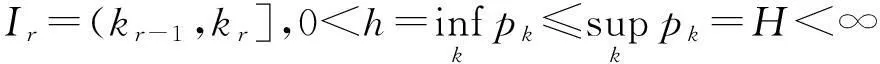
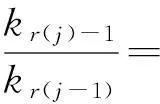
22j-1((2j)2j-1-2)>

((2j)2j-1-2)>j。

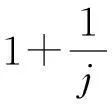
定义模糊数列

记模糊数

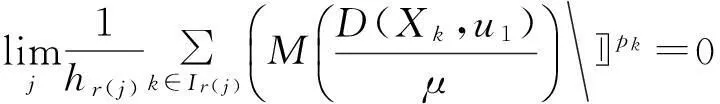
注意到，u1≠u2,从而模糊数列X={Xk}非强缺项收敛。

设n是一个充分大的整数,j是唯一确定的整数并且kr(j)-1

所以,对任意的ε>0，存在N，当n>N时，

综上，模糊数列X={Xk}强收敛而非强缺项收敛。

定理11设θ是缺项数列。若lim suprqr<∞,则F(M,θ,p)⊂F(M,p)。当lim suprqr=∞时，结论不一定成立。

N2+…+Nr0+Nr0+1 +…+Nr}≤

F(M,θ,p)⊂F(M,p)。

注意到qr>r(r=1,2,3,…),定义模糊数列

Xk(t)=

另一方面，可以证明数列X={Xk}非强收敛。若X0(t)=u1(t),则

若X0(t)=u2(t),则

若X0(t)≠u1(t)、u2(t)，0<ε

因此，由以上三种情况可知模糊数列X={Xk}非强收敛。

5结论

作为缺项统计收敛模糊数列空间的推广，本文基于Orlicz函数，在定义模糊数列强缺项收敛的基础上，提出和讨论三类基于Orlicz函数的模糊数列空间F(M,θ,p)、F0(M,θ,p)和F∞(M,θ,p)，并证明了空间的线性性质。通过研究模糊数列强缺项收敛与缺项统计收敛之间、强缺项收敛与强收敛之间的相互关系，得到了基于Orlicz函数的模糊数列空间F(M,θ,p)与缺项统计收敛模糊数列空间S(θ)之间的相互关系。讨论了空间F(M,p),F0(M,p),F∞(M,p)的性质以及空间F(M,θ,p)与F(M,p)之间的相互关系。并且，通过算例进行了说明。

参考文献:

[1] Fast H.Sur le convergence statistical[J].Colloqium Mathematicum,1951,2(1):241-244.

[2] Connor J.Two valued measure and summability[J].Analysis,1990,10(4):373-385.

[3] Fridy J A.On statistical convergent[J].Analysis,1985,5(4):301-313.

[4] Fridy J A.Statistical limit points[J].proceedings of the American Mathematical Society,1993,118(4):1187-1192.

[5] Fridy J A,Orhan C.Lacunary statistical summability[J].Journal of Mathematical Analysis and Applications,1993,173(2):497-504.

[6] Miller H I,Orhan C.On almost convergent and statistically convergent subsequences[J].Acta Mathematica Hungarica,2001,93(1/2):135-151.

[7] Balcerzak M,Dems K,Komisarski A.Statistical convergence and ideal convergence for sequences of functions[J].Journal of Mathematical Analysis and Applications,2007,328(1):715-729.

[8] Das P,Savas E,Ghosal S K.On generalization of certain summability methods using ideals[J].Applied Mathematics Letters,2011,24(9):1509-1514.

[9] 吴从灯，马明.模糊分析学基础[M].北京：国防工业出版社，1991:56-70.

[10] 巩增泰，白玉娟.模糊有界变差函数全变差的积分表示与距离导数[J].数学学报，2011,54(4):633-642.

[11] Savas E.On statistically convergent sequences of fuzzy numbers[J].Information Sciences,2001,137(1/4):277-282.

[12] Aytar S,Mammadov M A,Pehlivan S.Statistical limit inferior and superior for sequence of fuzzy numbers[J].Fuzzy Set and Systems,2006,157(7):976-985.

[13] Anastassiou G A,Duman O.Statistical fuzzy approximation by fuzzy positive linear operators[J].Fuzzy Set and Systems,2008,55(3):573-580.

[14] Kumar V,Kumar K.On the idea convergence of sequences of fuzzy numbers[J].Information Sciences,2008,178(24):4670-4678.

[15] 巩增泰，张璐.模糊数值函数的统计收敛[J].云南大学学报：自然科学版，2011，33(4):383-388.

[16] Nuray F.On sequences of fuzzy numbers[J].Fuzzy Set and Systems,1989,33(1):123-126.

[17] Kwon J S,Shim H T.Remark on lacunary statistical convergence of fuzzy nubmers[J].Fuzzy Set and Systems,2001,123(1):85-88.

[18] 巩增泰，刘晓霞.模糊数列的理想统计收敛和理想缺项统计收敛[J].山东大学学报:理学学报，2012,47(6):111-116.

[19] Lindenstrauss J,Tzafriri L.On Orlicz sequence spaces[J].Israel Journal of Mathematics,1971,10(3):379-390.

[20] Parashar S D,Choudhary B.Sequence spaces defined by Orlicz functions[J].Indian Journal of Pure and Applied Mathematics,1994,25(4):419-428.

[21] Mursaleen M,Khan Q A,Chishti T A.Some new convergent sequences spaces defined by Orlicz functions and statistical convergence[J].Italian Journal of Pure and Applied Mathematics,2001,9:25-32.

[22] Tripathy B C,Mahanta S.On a class of sequences related to thelp spaces defined by Orlicz function[J].Soochow Journal of Mathematics,2003,29(4):379-391.

[23] 吴从忻，王廷辅,陈述涛.Orlicz空间几何理论[M].哈尔滨：哈尔滨工业大学出版社，1986.

[24] Niven I,Zuckerman H S.An introduction to the theory of numbers[M].4th ed. New York:John Willey and Sons,1980.

[25] Mursaleen M,Basarir M.On some new sequence spaces of fuzzy numbers[J].Indian Journal of Pure and Applied Mathematics,2003,34(9):1351-1357.

〔责任编辑宋轶文〕

第一作者：许永红，女，副教授，研究方向为数学物理。E-mail:slxxyh@163.com