岩土体颗粒破碎的离散元数值模拟技术综述

郑麟 赵振营

摘要：该文概述了岩土体颗粒破碎的理论研究价值及工程意义。结合颗粒破碎物理试验研究现状，综合阐述了目前数值模拟技术的优势和方法，并认为离散元方法的数值模拟可以更有效的对岩土体颗粒破碎进行研究。总结分析了在离散元方法中研究颗粒破碎的两种方法，黏结模型和颗粒破碎模型。

关键词：颗粒破碎离散元数值模拟

中图分类号：P61 文献标识码：A 文章编号：1672-3791（2015）01（c）-0000-00

Review of particle breakage of rock and soil under

DEM analysistechniques

Zheng Lin， Zhao Zhen-ying

（School of Ocean Science and Engineering， Shanghai Maritime University， Shanghai 201306， China）

Abstract： This paper outlines the significance of particle breakage of rock and soil in theory and engineering. Combined with the presentexperimental study on particle breakageof physics， synthetically expounds the advantages of the numerical simulation technology， and the method of DEM can be more effective to study the particle breakage of rock and soil. Two methods of particle breakage in DEM was summarized and analyzed， the bond modeland the particle failure criterion.

Key words：Particle breakage； DEM； Numerical simulation

岩土材料（包括粘土和砂土）是粒状土颗粒的集合体。作为一种摩擦材料，它具有压硬性和剪胀性（含剪胀与剪缩）。除岩土颗粒本身的力学性之外，岩土颗粒间相互作用的力学特性、颗粒间相互接触的方式等也是影响岩土宏观力学特性的重要因素。

在很小主应力的条件下，岩土颗粒不容易發生破碎，只有岩土颗粒间的互相作用才能决定土的变形以及强度。而有较大平均主应力的时候，就很容易导致砂土颗粒的破碎，在这种条件下，除了颗粒之间的相互作用是影响砂土变形和强度的主要原因外，还有颗粒破碎对砂土力学特性的影响。相比砂土而言，粘土有很小的颗粒粒径，因此破碎现象不容易发生，只是在压力作用极其高的情况下，才会对粘土颗粒发生破碎影响了变形和强度进行考虑。然而在工程实际中会较多地出现砂土颗粒破碎的现象，现在已经有很多学者对岩土颗粒的破碎现象进行了相应的研究。

伴随着规模不断扩大的堤坝、隧道等，高压应力下的岩土工程课题也越来越多，岩土颗粒材料在高应力下的物理力学特性研究也变得越来越重要。颗粒材料在高应力水平下的一种基本现象是颗粒破碎现象，对颗粒材料的力学特性受破碎情况的影响进行分析，不仅有实际工程价值，还具有理论研究意义。

1物理试验研究现状

Terzaghi[1]对砂样进行压力高达96.5MPa一维压缩试验时，发现有十分明显的颗粒破碎现象。另外，他发现孔隙比与有效应力的对数坐标的斜率在高应力水平下，在应力的增长下增加是很微小的。DeSouza[2]对三种不同的砂进行了压力高达138MPa的试验。结果显示，在压缩的过程当中，压缩指数发生变化的地方出现了一个破碎点。分析颗粒结果表明，在应力高于破碎点的时候，具有十分显著的破碎现象；有较高的相对密度，则对应的破碎点的应力也就越高；增加颗粒棱角度会降低破碎点的应力。Harremoes研究了颗粒矿物成分对其破碎特性的影响，发现在高达138MPa应力的作用下，改变矿物和晶体尺寸不会对破碎点的应力造成影响。不过破碎点以上，具有十分明显的大量裂隙颗粒的破碎现象。Roberts对相同材料进行了试验，压力达到276MPa，与Harremoes和De Souza的结果非常相似。与此同时，DeBeer[3]为了验证Terzaghi提出的说法，即可以忽略不计在9.8MPa的应力以下产生的破碎；在9.8 MPa以上，随着应力的增加，极大地降低了破碎。他对均匀砂样进行了一维压缩试验，发现应力为15MPa时，会产生十分明显的破碎现象，但是在34MPa以上，伴随着应力的增加会渐次降低破碎。

综观目前对颗粒破碎的研究进展，很容易发现人们的注意点主要是在对产生破碎的影响因素的认识上，对破碎本身机理系统性的认识则比较缺乏。颗粒破碎对岩土体力学性质的影响等方面做得还很不够，尤其是没有深入研究微观破碎机理。当前的研究成果还远远不能说明岩土体颗粒破碎的力学机理，与实际工程的应用还有很远的距离。

2数值模拟方法

随着数值模拟方法以及高性能计算机的发展，岩土颗粒破碎力学特性研究对数值模拟方法的应用越来越广泛。由于室内试验难以从细观结构角度来分析认识颗粒破碎现象的机理和带来的力学特性的变化，数值模拟的方法可以有效地解决这些问题，为研究岩土体颗粒破碎的力学特性提供了途径。目前，用于岩土力学的数值模拟方法主要有FEM（有限元）和DEM（离散元）。

2.1有限元方法

解决数学物理和工程问题的数值方法叫做有限元方法，也称为有限单元法，是矩阵方法在弹性力学和结构力学等领域中的应用和发展。因其有效性和通用性，有限元方法被广泛地应用在了工程分析中，已成为计算机辅助制造和计算机辅助设计的重要组成部分。

将求解区域离散为一组有限个，且按一定方式互相联接在一起的单元组合体，是有限元方法的基本思想。由于能按不同的联接方式组合各单元，且可以具有形状不同的单元，所以可以几何形状复杂的求解域进行模拟。利用在每一个单元内假设近似函数来分片地表达求解域上的未知场函数，是有限元方法作为数值分析方法的一个重要特点。

闫澍旺在特制的压缩仪中对其压缩特性进行了试验，不同粒径组试样的相应的变形模量和屈服应力，颗粒级配情况，破碎规律进行了研究，还通过弹塑性有限元分析对石料破碎的规律性进行了分析验证。米占宽[4]基于Ueng和Chen剪胀方程，通过分析三轴剪切试验过程中的能量平衡，提出了考虑颗粒破碎的剪胀方程及其参数确定方法。通过对比分析三轴CD剪切试验成果，和分析工程实例的有限元数值，表明所提模型对材料的剪胀特性有较好的反映。贾宇峰[5]在土体的能量平衡方程中引入颗粒破碎耗能，进而根据能量方程建立了考虑颗粒破碎的粗粒土本构模型。同时结合三轴试验，根据剪切过程中的能量平衡关系，建立了考虑颗粒破碎影响的摩擦系数公式，对模型参数进行确立，验证了模型是有效的。

2.2离散元方法

基于分子动力学原理，美国学者Cundall [6-7]提出了离散单元法，是对岩石力学问题进行分析的一种间断性数值模拟方法。De Josselin de Jong和Verrujit[8]所做的光弹试验验证了此种方法的可靠性。因离散单元法在离散物质分析方面具有一定的优势，已成为近来年解决非连续介质问题的一种有效的数值模拟方法。PFC2D是以离散元方法为基础，基本单元为刚性圆盘或圆球，通过基本单元的相互作用和运动对实际问题进行模拟的离散元软件[9]。离散单元法首次提出是用来分析岩石力学，之后发展迅速，应用领域越来越广泛。Cundall和Strack [10]又将其应用到土力学中，并开发了二维圆盘程序BALL和三维圆球程序TRUBAL，这就是颗粒流程序PFC的雏形。

3 颗粒破碎在离散元数值模拟中的方法

离散元方法在岩土工程领域得到了广泛应用，现在已经成为岩土工程领域数值模拟的有效方法。目前，基于离散元方法来模拟颗粒破碎的途径有黏结模型和颗粒破碎模型。

3.1黏结模型

将基于若干离散颗粒通过接触点粘结形成的颗粒簇视为一个可破碎颗粒，在外力作用下该颗粒簇内某个接触点处的相互作用力满足一定强度条件时，则解除该接触点的粘结（可认为发生一个断裂事件）。当某部分颗粒或某个颗粒与其余部分颗粒间的接触粘结都解除后，则从原来的颗粒簇破碎出该部分颗粒或该颗粒[11]。

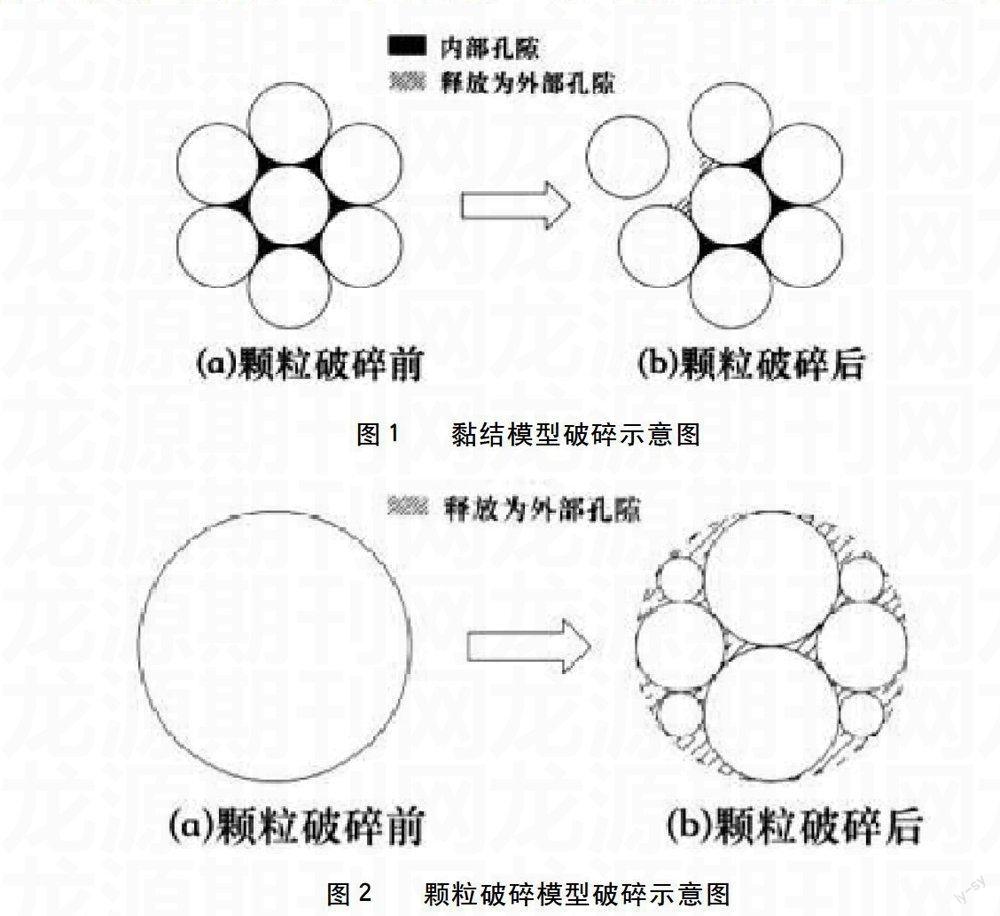
图1给出了黏结模型发生破碎的示意图。在加荷开始之前，簇颗粒沒有破碎，颗粒簇的实体面积应包括颗粒簇内部孔隙的面积，见图1（a）；开始加荷后，颗粒簇会在荷载增加到一定程度时产生破碎，这时，就会释放出原来归属于颗粒簇实体面积的那部分内部孔隙，形成试样的外部空隙，见图1（b）所示。在内部空隙不断释放的同时，会不断减小试样中的实体总面积。

图1黏结模型破碎示意图

李凡[12]基于PFC理论，利用颗粒黏结模型，通过记录试样黏结破损的数目和空间位置来反映结构性岩土材料破损特性。刘君[13]利用黏结模型对粗粒料进行数值模拟，发现颗粒破碎的细观演化规律和破碎带的分布范围。BuddhimaIndraratna[14]运用黏结模型形成二维尖角颗粒模型，利用细观力学参数如接触力和粘结力的分布在循环荷载作用下的发展来解释颗粒破碎的力学机制。

3.2颗粒破碎模型

基于单个离散颗粒，当其所有接触点处的接触力满足一定条件时，认为该颗粒将发生颗粒破碎模型的破碎[15]。这是由Lobo Guerrero[16]提出的颗粒破碎模型的方法，当颗粒达到破碎条件以后，原颗粒用8个小颗粒进行替代，由此来模拟颗粒破碎的现象。颗粒破碎模型的方法很好的解决了颗粒数量以及发生多级破碎的问题。

图2给出了颗粒破碎模型发生破碎的示意图。由于颗粒破碎是沿着颗粒中的孔隙发生破坏，破碎后颗粒中的孔隙会释放出来，变成试样的外部孔隙，阴影部分表示颗粒中的孔隙。

图2颗粒破碎模型破碎示意图

Lobo Guerrero [16]考虑了配位数对颗粒破碎的影响并基于假定的颗粒破碎模型考察了颗粒破碎演及其对颗粒材料力学行为的影响。Subero与Ghadiri[17]考察了冲击速度对颗粒破碎模型的影响，并总结了规律。

4 结语

离散元发展到如今相对于有限元有着它的巨大优势。有限元在研究砂土的力学特征时，采用的是连续介质理论，造成剪切强度和变形的细观力学机理无法从颗粒层面进行揭示，而对颗粒形状、孔隙率等试样要素变化对模拟结果的影响也无法反映出来。不过离散元刚好弥补了这一问题，可以从细观参数的研究来分析颗粒材料的宏细观力学特性，在分析岩土体大变形破坏问题及其宏细观机理研究方面具有独特的优势。

在模拟破碎时，黏结模型不用对破碎模式进行考虑，可由计算自动获得破碎后产物的分布和尺寸，但其与颗粒簇内单个颗粒尺寸分布有关系，并和颗粒间的强度分布关系紧密，再加上颗粒簇内的每个离散颗粒均参与将颗粒簇内的每个离散颗粒都参与接触力的更新、位置的更新及接触判断，故使计算量庞大。在计算量上颗粒破碎模型的方法则具有一定的优势，不过需要对颗粒破碎模式和破碎准则进行定义，而颗粒的应力分布与微细结构决定了颗粒是否破碎及按照何种模式破碎。但颗粒破碎模型把破碎前的颗粒视为完整的，没有考虑微细结构，且经典离散单元把颗粒视作刚体，虽对基于单个颗粒的名义应力进行了定义，但没给出颗粒内名义应力的分布。从变形体角度考虑，颗粒内部应力分布与颗粒表面接触力的大小及分布密切相关，由此可知颗粒破碎及破碎模式与颗粒配位数有关。

参考文献：

[1] TERZAGHI K， PECK R B. Soil mechanics inengineering practice[M]. NewYork： John Wiley and Sons Inc， 1948： 65-67.

[2] DE SOUZA J M. Compressibility of sand at high pressure[D].Massachusetts Institute ofTechnology， 1958.

[3] DeBeerEE.Thescaleeffectinthetranspositionofthe resultsofdeepsoundingtestsontheultimatebearing capacityofpilesandcaissonfoundations [J]. Geotechnique， 1963， 13（1）： 39-75.

[4] 米占寬， 李国英， 陈生水. 基于破碎能耗的粗颗粒料本构模型[J]. 岩土工程学报， 2012， 34（10）： 1801-1811. （MI Zhan-kuan， LI Guo-ying， CHEN Sheng-shui. Constitutive model for coarse granular materials based on breakage energy[J].ChineseJournalofGeotechnicalEngineering，2012， 34（10）：1801–1811. （inChinese））

[5] 贾宇峰. 考虑颗粒破碎的粗粒土本构关系研究[D]. 大连： 大连理工大学， 2008. （JIA Yu-feng. Coarse granular soil constitutive model incorporating particle breakage[D]. Dalian： Dalian University of Technology， 2008. （in Chinese））

[6] Cundall PA. A computer model for simulating progressive large scale movements in blocky system.Proceedings of Symposium of the International Society of Rock Mechanics. Rotterdam： A.A. Balkema， 1971（1）： 8-12.

[7] Cundall PA. The measurement and analysis of acceleration in rock slopes. Ph.D. Dissertation， University of London， Imperial college of Science and Technology， 1971.

[8] Cundall PA， Strack O D L. A discrete numerical method for granular assemblies[J]. Geotechnique， 1979， 29（1）： 47-65.

[9] ItascaConsulting Group， Inc. PFC2D theory and background. Minneapolis： Minnesota， 2004.

[10] 杨全文. 离散元法干颗粒接触模型研究及微机可视化程序设计[D]. 中国农业大学， 2001.

[11] ChengYP，BoltonMD，NakataY.CrushingandplasticdeformationofsoilssimulatedusingDEM[J]. Geotechnique， 2004， 54： 131-141.

[12] 李凡. 岩土材料破损特性的颗粒流研究[J]. 土木工程学报， 2007， 40（9）： 78-81. （Li Fan. A study on the breakage properties of geological materials using particle flow simulation[J]， China civil engineering journal， 2007， 40（9）： 78-81. （in Chinese））

[13] 刘君， 刘福海， 孔宪京. 考虑破碎的堆石料颗粒流数值模拟[J]. 岩土力学， 2008， 29（增）： 107-112. （Liu Jun，LiuFuhai，KongXianjing.Particleflowcodenumericalsimulationofparticlebreakageofrockfill[J]， Rock and Soil Mechanics， 2008， 29（增）： 107-112. （in Chinese））

[14] J. Lackenby， B. Indraratna， G. McDowell， D. Christie. Effect of confining pressure on ballast degradation and deformation under cyclic triaxial loading[J]. Géotechnique， 2007， 57（6）： 527-536.

[15] McdowellGR，BoltonMD，RobertsonD.Thefractalcrushingofgranularmaterials[J].Journalofthe Mechanics and Solids， 1996， 44： 2079-2102.

[16] Lobo G S. Evaluation of crusing in granular materials using the discrete element method and fractal theory[D]. University of Pittsburgh， 2006.

[17] Subero J， Ghadiri M. Breakage patterns of agglomerates[J]. Powder Technology， 2001， 120： 232-243.