小型水库土石坝稳定分析

小型水库土石坝稳定分析

李世娟

(辽宁省凌源市水利局， 辽宁 凌源122500)

【摘要】本文结合工程实例，对大坝稳定性计算方法、计算模型、工况和参数进行了详细说明，并针对渗流计算、坝坡稳定计算结果对坝体稳定情况进行了分析。

【关键词】水库； 土石坝； 稳定分析； 二维有限元法

中图分类号：TU457文献标志码： A

Analysis of the Stability of Small Reservoir Earth-rock Dam

LI Shi-juan

(LiaoningLingyuanWaterConservancyBureau,Lingyuan122500,China)

Abstract：In the paper, project examples are combined for describing dam stability calculation method, calculation model, working conditions and parameters in detail. Dam stability condition is analyzed aiming at seepage calculation and dam slope stability calculation results.

Keywords：reservoir; earth-rock dam; stability analysis; two-dimensional finite element method

1工程概况

小型水库均质土石坝高15m，坝顶长、宽分别为91.50m和2m，坝顶高程99.80m，设计、校核洪水位分别为98.45m和99.07m，正常蓄水位97.40m，下游水位85.00m，总库容40万m3，是一座兼具防洪、灌溉、供水等综合利用功能的水利工程。由于使用年限较长，水库的上游坝面、下游坝坡分别出现了塌陷和鼓凸、拉裂问题，其中下游坝坡的蠕变非常明显，而且右坝肩渗水现象较为突出，对水库使用功能的发挥、下游群众生命财产安全构成了一定威胁。

2稳定性计算方法

2.1坝体稳定渗流场

采用有限元法对大坝渗流进行计算。由于使用年限较长，可以将土体状态视为完全固结。此次研究所采用的二维均质土石坝稳定渗流方程如公式(1)所示，符合达西定律：

(1)

式中h——水头；

Q——流量；

kxy、kxx、kyy、kyx——以x、y轴为主轴的渗透系数。

公式(2)、公式(3)分别用于水头、流量边界的计算：

(2)

lxvx+lyvy=vn

(3)

式中h0——已知水头；

vx、vy——流速(分别沿x、y方向)；

lx、ly——渗透坡降(分别沿x、y方向)；

vn——流速(沿合向量方向)。

通过求解式(4)，可以计算稳定渗流场：

F=kh

(4)

式中k——渗透系数；

F——已知常数项，通过已知水头结点求得。

各节点的渗透坡降与流速可以在求出h后分别解出，渗流场自由面上压力p=0，且无渗流量通过，满足vn=0和h=y。

2.2坝坡稳定性

结合《碾压式土石坝设计规范》(SL 274—2001)的相关要求，该研究对于大坝抗滑稳定水平通过简化毕肖普法进行计算，边坡稳定性计算采用有效应力圆弧滑裂面法进行：

(5)

(6)

式中K——安全系数；

C、φ——分别为黏聚力和内摩擦角；

W——条块重力，根据条块位于浸润线上、下的实际情况，分别取重度、饱和重度；

U、D——分别为条块浮力和渗透力；

α——条块渗透力与水平线间夹角；

θ——条块重力线与底面夹角；

b——土条宽度。

3计算模型、工况和参数

3.1计算模型

X轴正向选为顺水方向、Y轴正向为竖直水流向上方向，原点设于0高程水平面，以0.5～1倍坝基长度为地基的有效深度。结合坝基地质情况，将坝体上下游河床以及坝基深度20m范围作为计算区域。渗流计算涉及1650个单元，786个有限元网络节点。

3.2计算工况与参数

该研究中，以正常蓄水位稳定渗流期、正常蓄水位+7级地震、校核洪水位骤降至正常蓄水位三种工况作为上游坝坡的计算工况；以设计洪水位稳定渗流期、设计洪水位+7级地震、校核洪水位稳定渗流期三种工况作为下游坝坡的计算工况。

根据地质勘查报告，对地基、坝体的材料物理力学指标、渗透系数进行确认，具体数值如表1所列。

表1　材料物理力学指标、渗透系数

4计算结果

4.1渗流计算结果

通过二维有限元软件，对水库三种工况进行渗流分析，得出流速矢量图、坝体水力梯度、坝体最大坡降、坝体单宽流量等的计算结果，详见表2。

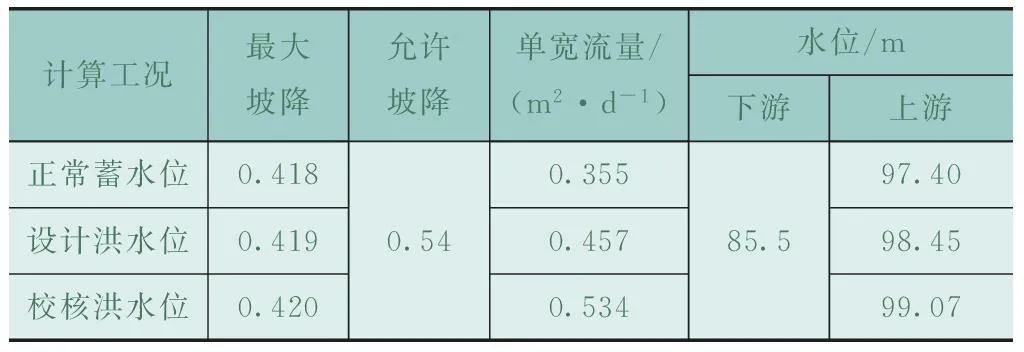
表2　最大坝高断面渗流计算结果

注: 坐标原点设于土石坝淤积面和上游面的交汇点，下游方向为X轴正向、竖直向上为Y轴正向。

由计算结果可以看出，坝体的单宽流量相对较小，最大坡降、抗渗性能均可满足相关要求，但浸润线出溢点相对较高，在三种工况下均位于下游坝体高程90m附近，若保护措施不得当，就非常容易出现渗透破坏的问题。结合水库运行报告及工作人员的实践经验可知，人为破坏是导致渗透坡降、浸润线相对较高的主要原因，目前，内坡反滤层坝面已经全部被人为破坏，下游坝脚排水棱体的使用功能也因人为破坏丧失殆尽。另外，由于水库建设时相关技术水平有限等原因，坝体的填筑质量已经无法满足现行标准的要求，渗透系数相对较高。

根据流速矢量图，可确认重点防护的对象为溢点高程90m左右处；水力梯度最大值为0.42，位于坡脚处，表明下游坝体内大部分区域为饱和，无法保障坝体稳定性，且极易出现渗透破坏问题。

渗透破坏、水力坡降间存在着密切的联系，通过水力坡降，可以预判渗透破坏的易发区域。由于X、Y方向的最大坡降分别位于坝体下游坡脚及下游岩体，因此，应于坡脚处进行排水棱体的设置，以便降低浸润线高度。综上所述，水库渗流稳定性不佳，则坝坡失稳问题容易发生。实践证明，水库运行经历与该研究所得结论一致，证明了该研究方法具有科学性及有效性特征。

4.2坝坡稳定分析结果

坝坡稳定分析以渗流分析的结果为依据，通过简化毕肖普法对三种工况下坝坡稳定性进行计算，部分计算结果如右表3所列。

5结语

综上所述，大坝存在着出现渗透破坏的可能性，所以在水库日常管理工作中，技术人员要对下游坡脚的

表3　最大坝高断面稳定安全系数

注： 其他工况下的稳定要求在以上三种工况的稳定要求得到满足时即可得到满足，因此仅对以上工况进行计算。

整体排水设施尤其是排水棱体进行全面检查和维护，或采取相应措施重点对下游坝坡稳定性与防渗等方面进行加固处理，彻底消除目前存在的安全隐患，充分发挥大坝的工程效益。

参考文献

[1]闫转平.土石坝地震动力响应及稳定性分析研究[J].陕西水利，2013(5):107-108.

[2]邵鹏.病险土石坝加固前后的渗流和坝坡稳定分析[J].黑龙江科技信息，2013(20):215-215.

[3]王鑫,梁军，等.有限元法在土石坝渗流稳定分析中的作用[J].治淮，2013(7):32-33.

[4]倪岩.水利工程中土石坝坝坡稳定分析[J].民营科技，2013(6):122-122.