数学课堂提问应把握好“度”

沈玉梅

提问是数学课堂教学必不可少的组成部分.在教学过程中，教师精心设计提问，激发学生的探索欲望，有意识地为学生发现疑难、解决疑难提供桥梁和阶梯.下面结合自己的教学实践就数学课堂提问的难度、梯度、密度的把握谈点认识与体会.

一、掌握好问题的难度

课堂提问难度要适中.课堂提问内容要有难易差别，符合学生的年龄特点和认知水平.教师要在学生原有认知水平的基础上设计一些适合的问题，由浅入深，循序渐进，从而让学生的思维经历发现的过程，而不是感到高不可攀.

教师在备课前要认真研究教材，研究课标，研究学情，在课上要提出难度适中的问题，以便调动学生思维的积极性，让大多数学生经过一定的思考解决问题.

二、 设计好问题的梯度

学习活动是一个由易到难、由简单到复杂的过程.在教学中，对于那些具有一定深度和难度的内容，学生难于理解、领悟，可以采用化整为零、化难为易的方法，把一些复杂、较难的问题设计成一组有层次、有梯度的问题，以降低问题难度.

例如，从等腰三角形底边上任一点，分别作两腰的平行线，所形成的平行四边形周长与它的腰长之间的关系如何？说说你的理由.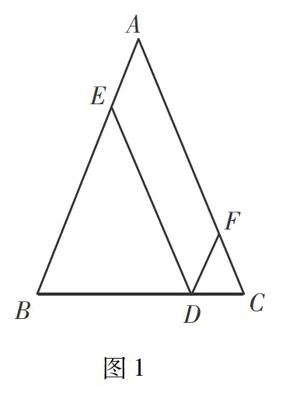

在教学过程中，可以将例题进行改编，注重提问的层次性，调动不同层次学生的学习积极性.已知等腰△ABC中AB=AC，D是底边BC上任一点，DE//AC， DF//AB.（1）如图1，这个图形中有你熟悉的数学图形吗？在此之前刚学习了平行四边形和等腰三角形，这个问题处于学习基础一般的学生的最近发展区，而且是一个开放题，让他们回答更能增强他们的学习积极性.引导学生找到等腰△EBD，等腰△FDC，AEDF，这样也为解决平行四边形周长与它的腰长之间的关系作好铺垫.（2）若点D在BC边上移动，请问图中有哪些量是不变的？这也是一个开放题，回答这个问题并不困难，让基础一般的学生有信心继续参与课堂.引导学生发现在等腰△ABC固定的情况下，图形中的各个角都没有变化.线段DE、DF、DC、DB随着点D的位置变化而变化.（3）点D在BC边上移动过程中，DE变短时，DF变长；DE变长时，DF变短，DE与DF的和是否不变？这一设问稍有难度，但在前两个问题的铺垫下，也能让更多的学生发现答案，进而解决了平行四边形周长与它的腰长之间的关系.

三、调节好问题的密度

提问虽然是课堂教学的常规武器，但是提问并非越多越好，主要是看提问是否引起了学生探索的欲望，是否能发展学生较高水平的思维，让学生学会分析问题、发现问题.课堂提问要适时适度，既不要太多，也不要太少，要把握好提问的时机，使提问发挥出最好的效果.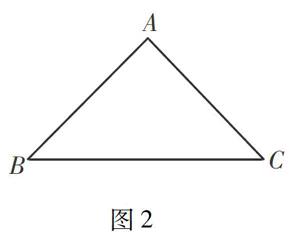

例如，在讲“等腰三角形的性质”时，有位教师这样设计提问（如图2）：师：在△ABC中AB=AC吗？ 生：是.师：AB=AC，那么∠B=∠C吗？生：相等.师：等腰三角形是轴对称图形吗？生：是.师：要说明∠B=∠C，作∠A的平分线行吗？生：行.师：可以作高吗……这种设计虽然表面上看热闹活跃，实际上流于形式，肤浅.把教学内容分析得过细，提出的问题过小，思维距很短，这固然能使学生易于应答，可以保证教学环节的有“序”进行，但也造成了许多失落，如活跃的想象、会心的沟通、不可言传的意会等.另一位教师是这样设计的：师：上节课学习了等腰三角形，知道它是轴对称图形，今天继续来学习它有什么性质.请同学们利用手中的等腰三角形纸板，小组合作去寻找答案.生：将它沿对称轴对折，发现左右重合，两个底角相等.师：很好！通过实验的方法发现，能再用数学知识加以说明吗？生：可以，作顶角平分线.生：还可以作高……这样的问题，给学生以充分自由选择的空间，引发学生参与讨论.学生经过深入思考，在答问时，展示的是自己理解、感悟的过程，训练的是思维、表达的能力.

总之，课堂提问无固定模式.根据学生的注意力容易集中在新鲜事物上的特点，教师可适当变换角度提问，增加提问的新颖性，训练学生思维的灵活性.