多粒度语言信息判断矩阵的满意一致性判定方法研究
2016-01-13唐燕武
唐 燕 武
(安庆师范学院 数学与计算科学学院, 安徽 安庆 246133)
多粒度语言信息判断矩阵的满意一致性判定方法研究
唐 燕 武
(安庆师范学院 数学与计算科学学院, 安徽 安庆 246133)
摘要:首先对多粒度语言判断矩阵定义了导出函数,相应地得到多粒度语言判断矩阵的互补导出矩阵,针对多粒度语言判断矩阵的互补导出矩阵,提出了多粒度语言判断矩阵满意一致性的新概念,并通过定义多粒度语言判断矩阵的偏好关系矩阵,给出了满意一致性的充分必要条件,进一步提出了多粒度语言判断矩阵的满意一致性的判定方法和基于满意一致性的语言判断矩阵方案优劣的排序算法。最后通过具体实例说明多粒度语言判断矩阵的满意一致性的判定方法和基于满意一致性的语言判断矩阵方案优劣的排序算法具有可行性与有效性。
关键词:决策分析;语言判断矩阵;偏好关系矩阵;导出矩阵; 满意一致性
一致性是群决策中度量语言信息判断矩阵科学性的一个重要指标,因此成为决策分析中的一个重要的研究课题。当前,对于语言信息判断矩阵的一致性研究已取得了比较丰富的研究成果[1-8]。如文献[1]和文献[2]分别研究了语言信息判断矩阵的完全一致性。文献[3]引入了语言信息判断矩阵的互反导出矩阵的概念,从而将语言信息判断矩阵转化为数量矩阵,进而提出了语言信息判断矩阵的一致性判定方法及其方案的排序方法。文献[4]给出了基于自然语言符号表示的比较矩阵的一致性判定方法及其方案的排序方法;文献[5]引入了语言信息判断矩阵的互反导出矩阵,提出了语言信息判断矩阵的有效的群决策方法。然而在决策中对多粒度语言信息判断矩阵的满意一致性的研究成果尚不多见。本文通过引入多粒度语言信息判断矩阵的互补导出矩阵和相应的偏好矩阵的概念,对决策中多粒度语言信息判断矩阵的满意一致性及其判定方法和方案排序方法进行研究。
1基本概念
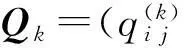

2主要结论
定理设矩阵A1为矩阵A0=A划去某一全零元素行及其相应列后所得的子矩阵,…,矩阵Ai+1为矩阵Ai划去某一全零元素行及其相应列后所得的子矩阵,则多粒度语言信息判断矩阵Qk=(qi j)n×n是满意一致性的充分必要条件为其偏好关系矩阵A=(ai j)n×n的所有阶子矩阵Ai皆有一行元素全部为零(i=0,1,…,n-1,n)。
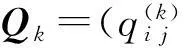
定理不仅给出了多粒度语言信息判断矩阵满意一致性的判定方法,还给出了满意一致性多粒度语言信息判断矩阵方案优劣的排序算法。
步骤3令i=0;
步骤4观察子矩阵Ai中的全0行,若存在,记此行所对应的方案为方案dun-1,并转步骤5,否则,转步骤6;
步骤5划掉子矩阵Ai中的全0行(若有多个全0行,则任选一行)及其相应列,同时令i=i+1。若i=n,则记此行所对应的方案为方案dun,这时可判定多粒度语言信息判断矩阵具有满意一致性,且决策者对方案集D={d1,d2,…,dn}优劣关系的方案优劣排序链为du1≥du2≥…≥dun,并可确定du1为最佳方案,结束。否则,转步骤4。
步骤6多粒度语言信息判断矩阵不具有满意一致性,结束。
3结束语
通过引入语言判断矩阵的互补导出矩阵,给出了多粒度语言信息判断矩阵的偏好矩阵的定义,提出语言信息判断矩阵的满意一致性的判定方法及其方案排序方法。
参考文献:
[1]陈岩,樊治平.语言判断矩阵的一致性及相关问题研究[J].系统工程理论与实践,2004,24(4):136-141.
[2]XuZS.Incompletelinguisticpreferencerelationsandfusion[J].InformationFusion,2006,7(3):331-337.
[3]唐燕武,陈华友. 语言判断矩阵的满意一致性判定方法研究[J]. 合肥工业大学学报, 2010(4):621-624.
[4]樊治平,肖四汉.基于语言符号表示的比较矩阵的一致性及排序方法[J].系统工程理论与实践,2002,22(5):87-91.
[5]陈岩,樊治平.基于语言判断矩阵群决策方法[J].东北大学学报(自然科学版)2004,25(3):303-306.
[6]陈侠,樊治平,陈岩.基于语言判断矩阵的专家群体判断一致性分析[J].控制与决策,2006,21(8):879-884.
[7]陈华友,赵佳宝.模糊判断矩阵的相容性研究[J].运筹与管理,2004,13(1):44-47.
[8]陈华友,刘春林.组合判断矩阵的相容性与一致性关系[J].系统工程理论方法与应用,2004,13(4):377-380.
[9]HerreraF,Herrera-viedmaE,MartinezL.Afusionapproachformanagingmulti-granularitylinguistictermsetsindecisionmaking[J].FuzzySetsandSystems, 2000,114(9):43-58.
[10]姜艳萍,樊治平.基于不同粒度语言判断矩阵的群决策方法[J].系统工程学报,2006,21(3):249-253.
[11]徐泽水.不确定多属性决策方法理论及应用[M].北京:清华大学出版社,2004.
[12]陈华友,刘金培,陈诚,语言判断矩阵的相容性和一致性研究[J],数学的实践与认识,2008,38(20):173-177.
[13]巩在武.不确定模糊判断矩阵理论方法研究[D].南京航空航天大学经济与管理学院,2006 : 152-158
[14]陈华友,刘春林. 基于相容性的模糊判断矩阵一致性改进新方法[J]. 模糊系统和数学,2005,19(2):122-126.
A Method of Determining Satisfying Consistency of Judgment Matrices
with Multi-Granularity Linguistic Terms
TANG Yan-wu
(School of Mathematics and Computation Science,Anqing Normal University,Anqing,Anhui 246133,China)
Abstract:First, the deduced function of multi-granularity linguistic judgment matrices is introduced, correspondingly, the deduced matrices of multi-granularity linguistic judgment matrices is defined. On the basis of these definitions, satisfactory consistency of multi-granularity linguistic judgment matrices and preference relation matrix are then presented. The sufficient and necessary conditions of a multi-granularity linguistic judgment matrix to fulfill satisfactory consistency are obtained. Furthermore, a judgment method is given to determine whether the linguistic judgment matrix has satisfying consistency. According to the judgment method, the approach for ranking alternatives based on the linguistic judgment matrix is also obtained. Finally, an example shows the effectiveness of the proposed method.
Key words:decision-making, linguistic judgment matrix, preference relation matrix, induced matrix, satisfied consistency
文章编号:1007-4260(2015)02-0016-03
中图分类号:N945;C945
文献标识码:A
作者简介:唐燕武,女, 安徽安庆人,硕士,安庆师范学院数学与计算科学学院副教授,研究方向为运筹与管理、预测和决策分析。
基金项目:安徽省高校省级自然科学研究一般项目(KJ2010B094)。
收稿日期:2014-07-29
