具有耐火钢短梁的钢框架梁柱连接抗火性能模拟

孔德阳++席丰

摘要： 通过有限元模拟探讨将耐火钢短梁应用于钢框架梁柱连接以提高连接抗火性能的可能性.考察三维有限元建模过程中模型简化、网格划分、求解方法和接触关系等关键技术，以提高计算效率并确保分析结果的可靠性.提出3个确定极限温度的准则并应用于钢框架，通过比较可知：对于采用普通钢的钢框架，采用准则1与准则2确定的极限温度与由最大挠度为L/20和L/10所确定的临界温度较接近，这有益于指导钢框架抗火设计.比较普通钢与耐火钢短梁的变形可知：耐火钢的使用可以有效控制跨中挠度变形，使最大变形值减小1/2以上.

关键词： 钢框架； 短梁； 梁柱连接； 耐火钢； 极限温度； 挠度； 三维有限元

中图分类号： TU391； TU392.6文献标志码： B

0引言

火灾条件下的梁柱连接对钢结构的行为起重要作用.众所周知，随着温度升高，普通钢材的强度和刚度都会降低，在600 ℃时其屈服强度约为常温下的1/2.同时，对许多钢结构建筑火灾后的现场调查也表明，一旦梁柱节点在火灾中发生破坏，将会导致建筑物发生整体坍塌.

国内外对于梁柱连接的研究很多.WANG等[1]和DAI等[2]对5种节点形式、2种柱尺寸的梁柱连接在高温下的连接行为进行系统的分析；王卫永等[3]对4个H型钢外伸端板连接进行高温下的试验研究，得出节点连接处的柱翼缘屈曲变形或端板受拉发生弯曲变形是火灾下外伸式端板节点破坏的主要因素；YU等[4]阐述如何利用Abaqus更好地模拟高温下的螺栓连接，介绍网格大小和算法选择等.CHUNG等[5]通过实验和模拟表明使用耐火钢可有效提高结构极限温度.

耐火钢在600 ℃时可以保证2/3常温下的屈服强度，利用耐火钢制作结构构件可以大大减少防火涂料的使用.然而，耐火钢比普通钢价格更贵，因此如何经济使用尤为重要，可以将结构中最为重要的区域代之以耐火钢.《建筑抗震设计规范》[6]中消能梁段（本文中将此构造形式作为一种特殊的梁柱连接方法，以下称之为短梁）的抗震构造设置为这种方式提供可能，见图1.

图 1钢框架梁柱连接，mm

Fig.1Beamcolumn connection in steel frame，mm

显然，用实验和数值模拟手段对该问题深入研究十分必要.本文尝试运用Abaqus进行有限元分析，为此将短梁分别设置为普通钢（试件A）和耐火钢（试件B），对H梁和H柱2种类型的梁柱连接进行有限元分析，以探索这一设想的可能性.模拟表明，试件B由于转角过大使得柱先于梁破坏，因而提出柱侧肋板加强形式，称为试件BJ.

1有限元模型

1.1几何模型

几何模型和螺栓布置见图2，肋板加强正视图和左视图见图3.H柱高为3 500 mm，截面尺寸为350 mm×350 mm×15 mm×19 mm，柱内与梁上下翼缘平齐位置设置加劲肋；梁长为2 400 mm，其中短梁长为400 mm，连接梁长为1 600 mm，截面尺寸为250 mm×175 mm×7 mm×11 mm；加劲肋尺寸为500 mm×80 mm×11 mm.短梁与柱通过焊接连接，短梁与连接梁之间上下翼缘采用焊接连接，腹板处通过螺栓端板进行连接，螺栓采用8.8级M16摩擦型高强螺栓.为防止加载处屈曲，梁腹板在加载处加设加劲肋.

图 2几何模型和螺栓布置，mm

Fig.2Geometric model and bolt distribution， mm

a）正视图b）左视图图 3肋板加强正视图和左视图，mm

Fig.3Front and left views of ribbed plate， mm

1.2材料模型

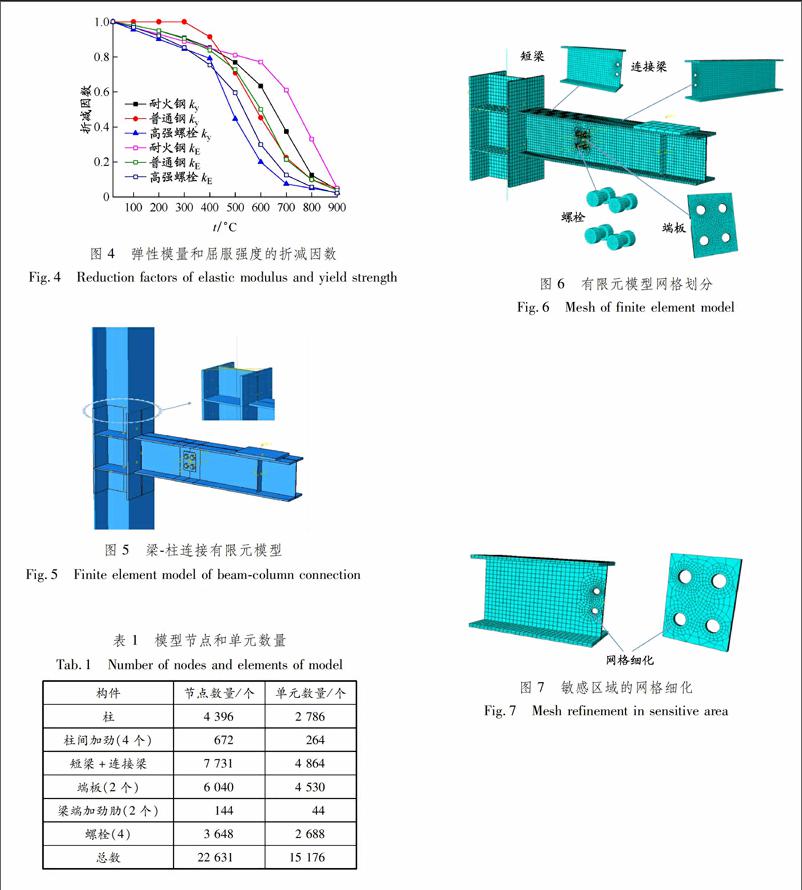
本文采用的钢材均为Q390，常温下屈服强度为390 MPa，弹性模量为210 GPa；高强螺栓屈服强度为940 MPa，弹性模量为210 GPa.采用理想弹塑性模型，泊松比均取为0.3，膨胀系数为1.45E-5.材料强度和弹性模量的折减均采用《建筑钢结构防火技术规程》[7]中的公式计算.弹性模量和屈服强度的折减系数见图4，其中ky和kE分别表示屈服强度和弹性模量的折减因数.

图 4弹性模量和屈服强度的折减因数

Fig.4Reduction factors of elastic modulus and yield strength

1.3有限元模型

为降低计算成本，取1/2结构建立有限元模型进行计算，并对有限元模型进行局部简化，见图5.柱的节点区域、梁、加劲肋和横隔板均采用三维8节点减缩积分单元C3D8R，柱的非节点区域则采用三维梁单元B31，并将二者的自由度耦合在一起.

图 5梁柱连接有限元模型

Fig.5Finite element model of beamcolumn connection

网格密度对于数值计算十分关键.网格敏感性分析结果表明：当柱网格大小为20～25 mm，梁和端板网格大小为15～20 mm时，计算精度和计算速度较适宜.试件有限元模型各部分节点和单元数量见表1.

表 1模型节点和单元数量

Tab.1Number of nodes and elements of model构件节点数量/个单元数量/个柱4 3962 786柱间加劲（4个）672264短梁+连接梁7 7314 864端板（2个）6 0404 530梁端加劲肋（2个）14444螺栓（4）3 6482 688总数22 63115 176为防止梁腹板过早屈曲，至少将腹板划分2层，见图6.需要注意的是，接触对附近的模型对网格质量尤为敏感，是模拟的关键.为此，须将短梁、连接梁和端板孔洞区域网格进行细化，见图7.endprint

图 6有限元模型网格划分

Fig.6Mesh of finite element model

结构模型存在诸多接触对：螺帽与端板间8个，螺杆与端板孔壁间8个，螺杆与短梁孔壁间2个，螺杆与连接梁孔壁间2个，端板与短梁腹板间2个，端板与连接梁腹板间2个.所有的接触关系都定义为“面面接触”，并选择小滑移理论.在螺帽与端板、螺杆与端板孔壁、螺杆与短梁孔壁及螺杆与连接梁孔壁接触对中，分别将前者定义为主面，将后者定义为从面；在端板与短梁腹板、端板与连接梁腹板接触对中，分别将短梁腹板和连接梁腹板的接触面定义为从面，将端板的接触面定义为主面.为使计算中的接触更容易建立，在螺帽与端板之间以及螺杆与各孔壁之间预留0.01 mm的空隙.在接触的切线方向采用Penalty摩擦模型，摩擦因数取0.3；将接触法线方向上定义为“硬接触”.

图 7敏感区域的网格细化

Fig.7Mesh refinement in sensitive area

1.4边界条件和加载

所有模型的箱型柱脚约束3个方向的平动自由度和平面外的2个转动自由度；柱顶部约束2个平面外转动自由度和2个平动自由度；梁跨中截面限制轴向位移和平面内转动.

模拟中加载分为4个分析步：施加螺栓预紧力；柱顶端施加轴向力50 kN；梁段线性加载至40 kN；将整个结构采用国际ISO834标准升温曲线进行升温.

2数值模拟结果

2.1模拟变形结果

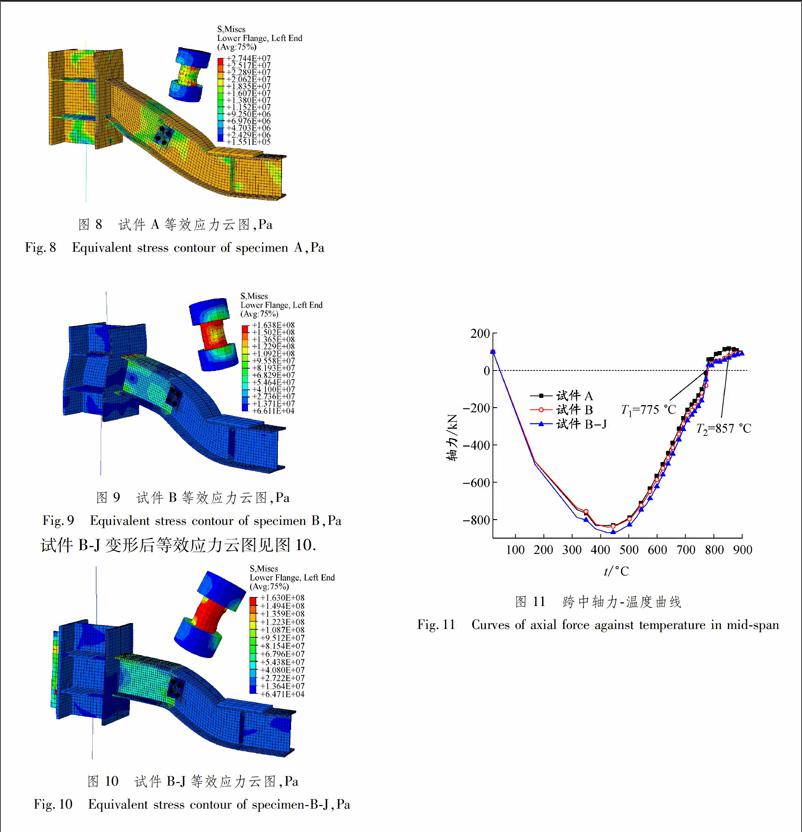
试件A变形后的等效应力云图见图8.最大应力发生在螺栓杆上，端板连接处未发生破坏或较大变形.短梁端部上翼缘由于轴拉力作用变形增加继而失去承载能力，在此过程中柱未见明显变形.

图 8试件A等效应力云图，Pa

Fig.8Equivalent stress contour of specimen A，Pa

试件B变形后等效应力云图见图9.最大应力出现在梁柱连接处以及螺栓杆上，螺栓受剪轻微变形，但端板连接整体尚好.跨中挠度增大主要由连接梁变形引起，短梁并无明显变形或者局部屈曲.当温度达到约850℃时，连接转角迅速增加至失去继续承载能力.

图 9试件B等效应力云图，Pa

Fig.9Equivalent stress contour of specimen B，Pa

试件BJ变形后等效应力云图见图10.

图 10试件BJ等效应力云图，Pa

Fig.10Equivalent stress contour of specimenBJ，Pa

图10与图9对比可以发现：柱侧加劲肋的使用可以有效控制柱间腹板屈曲问题，前者最大应力出现在加劲肋处而不是梁柱焊接区域，而且连接梁的塑性变形更大.

2.2依据极限温度判定准则的比较分析

2.2.1极限温度定义

对于极限温度的定义，GB 50016—2014[8]和文献[9]中是根据跨中挠度达到L/20（L为梁的跨长）原则确定的.事实上，此准则趋于保守，钢结构在大挠度情况下由于悬链性效应的影响仍能够继续承担载荷和变形而不发生倒塌.文献[10]中给出大挠度情况下2个临界温度的判定准则.

准则1：以悬链力开始出现时的温度作为极限温度，记为T1.

准则2：以悬链力达到最大值时的温度作为极限温度，记为T2.

对于钢框架节点来说，通常认为当相对转角达到0.6°或者0.1 rad时节点失效达到极限状态，可将这一标准作为准则3，记为T3.

通过计算得到跨中截面轴力温度曲线，见图11.图11中：3个试件的轴力温度曲线基本一致，在775 ℃时轴力为0，即T1=775 ℃；试件A，B和BJ分别在857，881和902 ℃时轴力达到最大值.为便于比较统一取其小者，即T1=857 ℃.

图 11跨中轴力温度曲线

Fig.11Curves of axial force against temperature in midspan

2.2.2转角温度曲线

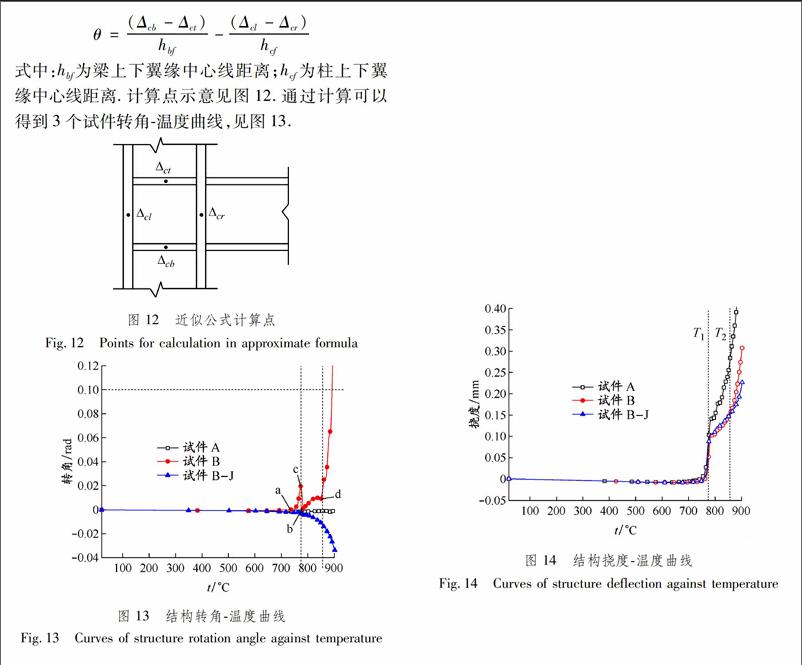
作为连接构件的重要组成部分，梁柱节点可以对弯矩、轴力和剪力进行传递，但由于所承受的轴向变形和剪切变形较小，通常只考虑转动变形对节点的影响.然而，不论在实验中还是在有限元分析中都很难准确计算出梁柱的相对转角.本文采用文献[11]推荐的如下公式进行转角计算并绘制曲线确定其极限温度.θ=（Δcb-Δct）hbf-（Δcl-Δcr）hcf式中：hbf为梁上下翼缘中心线距离；hcf为柱上下翼缘中心线距离.计算点示意见图12.通过计算可以得到3个试件转角温度曲线，见图13.

图 12近似公式计算点

Fig.12Points for calculation in approximate formula

图 13结构转角温度曲线

Fig.13Curves of structure rotation angle against temperature

对于试件A，转角在整个变形过程中相对保持不变，悬链线效应对转角基本无影响，悬链轴力没有传至柱端.对于试件B，当温度达到a点（738 ℃）之前与试件A转角温度曲线基本重合；当温度在a～b（738～775 ℃）范围内时，转角的增加主要是由于梁端负弯矩的作用；当温度在b～c（775～781 ℃）范围内时，连接梁腹板在荷载和温度的作用下开始屈服，塑性应变出现，柱端“反弹”而转角减小；当温度在c～d（781～851 ℃）范围内时，试件B转角增加而斜率逐渐降低，这是因为与普通钢相比，耐火钢在此时仍保持相对较大的刚度和强度，悬链轴力得以传递至柱端；当温度达到d（851 ℃）以后，试件B柱间加劲肋之间的腹板发生屈服变形（见图10），转角迅速增加继而失去承载能力.试件BJ在温度达到738 ℃后转角反而减小，最小值仅为0.034 rad.依据准则3得出试件A，B和BJ的极限温度分别为∞，895 ℃和∞.结合试件B的等效应力云图与挠度温度曲线可知：当温度达到895 ℃时，试件B转角变形速率过大，试件已失效，因此依据准则3确定的结构极限温度不适用.endprint

2.2.3挠度温度曲线

3个试件梁端部的挠度温度曲线见图14.3条曲线发展趋势基本相同：在温度达到约757 ℃之前，材料的刚度和强度满足承载要求，挠度基本没有增加；当温度达到约783 ℃之前，二者跨中挠度迅速增加；在温度达到h后，2条曲线斜率反而减小，这是由于大变形导致的悬链线效应开始发挥作用，试件A曲线的斜率小于试件B和BJ的斜率，因为此时耐火钢仍保持相对较大的刚度和强度，这与转角温度曲线分析吻合.当温度继续增加时，试件挠度迅速增加直至失去继续承载的能力.

图 14结构挠度温度曲线

Fig.14Curves of structure deflection against temperature

当温度为T1=775 ℃时，试件A挠度温度曲线出现第一次突变，此时挠度为0.1 m（L/24），与《建筑钢结构防火技术规程》和文献[10]中所推荐的特征值变量L/20较为吻合.同时，由图14可知，结构仍具有继续承载的能力，说明准则1的方法趋于保守.相对应的试件B和BJ的变形仅分别为0.05 m（L/48）和0.03 m（L/80）.

当考虑梁大挠度变形作用，即温度为857 ℃时，试件A的挠度为0.29 m（约为L/8.3），略大于文献中推荐的L/10标准，而试件B和BJ的挠度均仅为0.15 m（L/16）.显然，耐火钢短梁的使用可以有效控制梁跨中的变形.

3结论

运用Abaqus对将具有耐火钢的短梁应用于梁柱连接以提高钢框架抗火性能的设想进行数值模拟，对三维有限元建模过程中的模型简化、网格划分、求解方法和接触模拟等关键技术进行探索，并依据3个极限温度判定准则比较分析利用耐火钢前后的结构行为，得到以下结论.

1）对于普通钢框架，当采用本文螺栓连接形式时，由准则1所确定的极限温度与由最大挠度变形为L/20所确定的临界温度比较接近，偏于安全保守；由准则2所确定的极限温度略高于由最大变形为L/10所确定的临界温度.因此，对于与本文相同连接形式的钢框架结构，在允许梁过大变形的情况下，可采用最大变形为L/10的准则定义临界温度，否则可采用最大变形为L/20的准则判定临界温度.

2）数值模拟的结果表明，将具有耐火钢的短梁应用于钢框架连接可以有效控制跨中挠度变形，使最大挠度值减小1/2左右；另外，从变形图中可以看出，跨中挠度增加的主要原因是连接梁的屈服，而关键区域的耐火钢短梁并未出现破坏和大变形，这对于保持结构整体性、防止连续性倒塌具有重要意义.单纯的只提高梁节点区域材料耐火性能并不能提高钢框架整体抗火性能，需要对柱、梁综合考虑以达到少用或不用防火涂料的目的.柱侧肋板加强的方法可以有效避免这一不利情况的发生.

3）由于螺栓连接中存在大量的接触关系，使得螺栓连接的有限元模拟仍是一项挑战.文献[4]中推荐运用显示动力学算法求解螺栓接触问题，本文则推荐采用一般静力算法和隐式动力学相结合的方式进行求解，可以大大缩短计算时间.参考文献：

[1]WANG Y C， DAI X H. An experimental study of relative structural fire behavior and robustness of different types of steel joint in restrained steel frames[J]. J Constructional Steel Res， 2011， 67（7）： 11491163.

[2]DAI X H， WANG Y C， BAILEY C G. Numerical modelling of structural fire behavior of restrained steel Beamcolumn assemblies using typical joint types[J]. Eng Struct， 2010， 32（8）： 23372351.

[3]王卫永， 董毓利， 李国强. 外伸端板节点抗火设计方法[J]. 哈尔滨工业大学学报， 2008， 40（10）： 16251628.

WANG Weiyong， DONG Yuli， LI Guoqiang. A method for fireresistance design of extended endplate joints[J]. J Harbin Ins Technol， 2008， 40（10）： 16251628

[4]YU H， BURGESS I W， DAVISON J B. Numerical simulation of bolted steel connections in fire using explicit dynamic analysis[J]. J Constructional Steel Res， 2008， 64（5）： 515525.

[5]CHUNG H Y， LEE C H. Application of fireresistant steel to beamtocolumn moment connections at elevated temperature[J]. J Constructional Steel Res， 2010： 289303.

[6]GB 50011—2010建筑抗震设计规范[S].

[7]DG/TJ 08008—2000建筑钢结构防火技术规程[S].

[8]GB 50016—2014建筑设计防火规范[S].

[9]胡军. 梁柱栓焊混合边节点火灾响应特征研究[D]. 合肥： 中国科学技术大学， 2009.

[10]席丰， 栾艳萍. 受火侵袭两端完全约束钢梁大挠度行为的参数分析与极限温度准则[J]. 中国科学：技术科学， 2012， 42（2）： 202212.

XI Feng， LUAN Yanping. Criteria of limiting temperature and parametric analysis of the large deflection behavior for fully restrained steel beams in fire[J]. Scientia Sinica： Technol， 2012， 42（2）： 202212.

[11]施刚， 袁锋， 霍达， 等. 钢框架梁柱节点转角理论模型和测量计算方法[J]， 工程力学， 2012， 29（2）： 5260.

SHI Gang， YUAN Feng， HUO Da， et al. Theoretical model and measuring calculation method of the beamtocolumn joint rotation in steel frame[J]. Eng Mech， 2012， 29（2）： 5260.（编辑于杰）endprint