LMS算法在分布式光纤测温系统中的应用

LMS算法在分布式光纤测温系统中的应用

李金铸,胡兴柳,张小伟

(安徽工业大学 电气与信息工程学院,安徽 马鞍山243000)

摘要信号采集和数据处理是分布式光纤测温系统的核心,信号中的噪声决定了整个系统的测量精度,空间分辨率,采集速度及最终的请求响应时间。通常系统采集到微弱的温度信息的反斯托克斯信号会被完全淹没在噪声中。因此,得到含有温度信息的有用信号就显得尤为重要。文中针对系统中噪声信号的特征,提出一种变步长的最小均方根自适应滤波算法,对拉曼散射的温度信号进行去噪处理并进行Matlab仿真。仿真结果表明,该算法有效提高了去噪的效果,从而可提升整个系统的测量精度,空间分辨率。

关键词分布式测温;拉曼信号;自适应滤波;变步长;最小均方根

收稿日期:2015-02-05

基金项目:国家自然科学基金资助项目(61201109);2013安徽省级创新训练基金资助项目(201310360179)

作者简介:李金铸(1988—),男,硕士研究生。研究方向:智能控制与智能检测。E-mail:18055504827@163.com。胡兴柳(1974—),女,博士,教授。研究方向:光纤传感技术与智能控制。

doi:10.16180/j.cnki.issn1007-7820.2015.09.005

中图分类号TP274+.5

Application of LMS Algorithm in the Distributed Optical FiberTemperature Measurement System

LI Jinzhu,HU Xingliu,ZHANG Xiaowei

(College of Electrical and Information Engineering,Anhui University of Technology,Manshan 243000,China)

AbstractThe core of a distributed optical fiber temperature measurement system (DTS) is signal collection and data processing.The measuring accuracy,spatial resolution,collecting speed and final response time are all affected by the noise in signal.The anti-Stokes signal contains very weak temperature information and is often completely overwhelmed by noise.Therefore,getting the useful temperature information from the signal is particularly important.A variable step size least-mean-square (LMS) adaptive filtering algorithm is researched for the characteristic of the noise signal in distributed optical fiber temperature measurement system and used to denoise the Raman scattering temperature signal.Matlab simulation shows that this algorithm has good denoising performance and improves the system measurement accuracy and spatial resolution.

Keywordsdistributed temperature;Raman signal;adaptive filtering;variable step size;minimum rms

随着光纤技术的快速发展,分布式光纤测温技术在众多温度测量领域中得到了广泛应用,已成为温度测量的重要手段。与传统的传感器相比,光纤传感技术具有光学敏感测量和光纤传输的许多特点,如灵敏度高、电绝缘、抗电磁场干扰及易于实现远距离的分布式测量等[1]。基于 Raman 散射的分布式光纤传感测温系统(DTS)是一种实时测量沿光纤方向空间场温度的分布式传感器系统。其原理是高功功率窄脉宽激光光源发射一系列脉冲光,通过拉曼波分复用器(拉曼WDM)将脉冲光耦合进入传感光纤并接收光纤后向拉曼散射光谱,同时由拉曼WDM内光学滤波器,分别滤出斯托克斯光和反斯托克斯光,再由检测器件、放大电路将其转化为电信号并进行相应的处理,解调出与光信号对应的温度场信息。最终通过光的时域反射技术进行定位。

由于光在传输过程中的损耗、拉曼散射的功率非常小使后向散射回来的反斯托克斯光和斯托克斯光的信号非常微弱,这样光电转换后的电信号很难被检测。同时传感光纤弯曲处和焊接处损耗、传感器自身的噪声、放大电路的噪声、各种元器件的固有噪声以及光电转换和放大的过程中会引入随机噪声和外界的电磁干扰,这些噪声的幅度往往比有用信号的幅度大得多[2]。受到上述因素的影响,使得原本微弱的反斯托克斯信号和斯托克斯信号完全淹没在噪声中。因此,必须有效抑制信号中的噪声,才能提取出有用的温度信号,从而提高系统的性能。因此,对微弱信号的处理的关键就是提高系统的信噪比[3]。

自适应滤波算法在信号处理领域有着重要的地位,近年来在各领域都得到了广泛应用,如工业控制、通信领域以及导航系统等。对于不能预测信号以及噪声特点的场合,无法使用一般的滤波器对信号进行最优滤波,自适应滤波器的引入成为行之有效的方法。现有各种自适应滤波算法中,LMS和NLMS[4-5]由于其计算量小,易于实现而被广泛采用。根据分布式光纤测温系统的信号噪声特点,本文采用一种变步长的LMS自适应滤波算法对拉曼散射传感信号进行去噪。

1分布式光纤测温原理与信号特征

1.1　分布式光纤测温的原理

分布式光纤测温系统的原理如图1所示,主要由传感器光纤、拉曼WDM、高功率窄脉宽激光光源、光电转换器件雪崩二极管APD与放大电路、信号采集与数据处理系统等部分组成。激光器发出一系列高频大功率窄脉宽的脉冲光,经过拉曼WDM将光脉冲耦合进人传感光纤,由于传感光纤的背向拉曼散射,散射光通过光纤传输回拉曼WDM中分光器,分别过滤出斯托克斯光和反斯托克斯光,然后通过光电转换器雪崩二极管APD转换为电信号,电信号经过低噪声放大器后,再由高速A/D进行转换与信号采集模块将采集的数据送入信号处理单元进行处理,最后解调出与光电信号对应的温度信息并在计算机中显示。

图1　分布式光纤测温系统原理

1.2　拉曼噪声信号的特征

拉曼散射散射的光信号具有以下特点:信号的信噪比较低,信号的噪声主要是白噪声和瞬时脉冲,致使原本微弱的有用信号完全淹没在噪声中;一般情况下有用的信号是低频信号,而噪声是高频信号;噪声信号的强度由近到远逐渐增强。由于白噪声的产生是随机的,并具有平均值为零统计特性,为减少噪声对分布式测温系统性能的影响,通常采用数据累加平均算法来处理信号,从而提高系统温度分辨率。该算法主要通过累加次数来改善信号的信噪比,累加次数越多效果越好。累加次数越多,系统温度测量的时间越长,显然,在温度快速变化的场合此算法则不适用,系统的实际应用会受到影响。若得到响应速度较快的系统,一是必须损失系统的测温精度,二是要改进算法节约数据处理的时间。

1.3　白噪声序列

从工程实际出发,白噪声往往可视为具有理想谱密度的平稳随机过程。白噪声是一种简单的随机过程,是由一系列不相关的随机变量组成的理想随机过程。数学描述

Rξ(τ)=σ2δ(τ)

(1)

式中,δ(τ)为单位脉冲函数。白噪声离散化

Rξ(k)=σ2ξ(k),k=0,±1,±2,…

(2)

DTS中拉曼散射温度信号中的这些噪声可认为是白噪声,故本文采用零均值,方差为1的高斯白噪声,如图2所示,作为噪声信号进行去噪仿真。

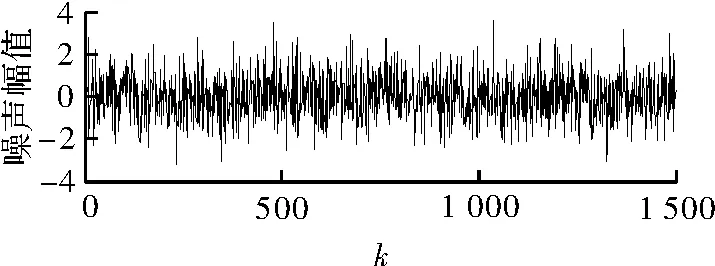
图2　白噪声序列

2变步长LMS自适应滤波器的原理

2.1　最小均方自适应滤波器的结构

自适应滤波技术已广泛地应用于数字滤波器设计、通信、系统辨识、自动控制及物理科学中。在工程中经常会遇到如下情况:输入信号是随机的,信号统计特性未知或者统计特性缓慢变化(非平稳信号)。这就使人们不得不研究处理这类信号的滤波器,应用于工程实践中。这类滤波器的特点:输入信号是统计特性未知的随机信号或者非平稳信号时,可以通过某中算法自适应的调整滤波器参数,来实现工程中的某种准则。由于这类滤波器能变动自身的参数以“适应”输入过程统计特性的估计或变化。因此,把这类滤波器称为自适应滤波器[6]。

LMS算法(Least Mean Square)是美国斯坦福大学的Widrow和Hoff在研究自适应理论时提出的,因其易实现而得到了广泛应用,并成为自适应滤波中的标准算法。其有两个基本部分组成:

(1)滤波过程。计算通过输入信号时滤波器的输出响应;然后,通过比较输出响应Y(n)与期望响应D(n)产生估计误差。

(2)自适应过程。根据估计误差E(n)自动调整滤波器自身权值。这两个过程缺一不可,协调工作组成一个反馈回路,

以上两个过程协调工作,缺一不可,其框图如图3(a)所示,首先由一个普通的横向滤波器来构造LMS算法,用它完成基本的滤波工作。其次,还有一个根据E(n)自动调整权值的控制算法来适应横向滤波器。

自适应滤波器的结构如图3(b)所示。输入向量X(n)的元素有N×1个,分别为抽头X(n),X(n-1),X(n-2),…,X(n-N+1),其中N-1是延迟单元的个数;这些抽头组成了一个多维空间。与输入向量对应的有N×1个权向量W(n),其分别是抽头权值W0(n),W1(n),W2(n),…,WN-1(n)。通过计算计算最小均方根得到一个向量的估计值,当迭代次数趋近与无穷多时,该估计值的期望值可能接近维纳解Wo。在滤波过程中,输入向量X(n)与期望响应D(n)同时作为滤波器的输入参考,这样给定一个输入信号,横向滤波器FIR就会输出一个作为期望响应D(n)的估计,然后将此估计值与期望响应作差,得到估计误差E(n)。

图3　自适应滤波器的原理图

2.2　最小均方自适应算法

本文综合文献[7～8]分析,在常规固定步长LMS或牛顿LMS自适应算法中,通常收敛速率与稳态误差之间相互矛盾并不能同时满足系统的要求,人们研究了各种各样的改进型LMS算法[9-11]。本文提出一种更为简便的变步长LMS算法,其迭代公式如下

Y(n)=wH(n)*X(n)

(3)

E(n)=D(n)-Y(n)

(4)

w(n+1)=w(n)+μ(n)*X(n)*E(n)

(5)

μ(n)=αμ0/en-1

(6)

式中,w(n)为自适应滤波器在时刻n的权值向量;X(n)为输入信号向量;D(n)为期望信号;E(n)为误差信号;μ(n)为使相应的定步长LMS算法收敛最快的步长;固定步长μ0表示最大允许的步长。α为调整因子,取值范围为0.9≤α≤1。LMS自适应滤波器有3个性能指标分别是收敛的速度,对时变系统的快速跟踪能力和收敛精度。变步长算法就是在无数次迭代过程中自适应调整步长,在滤波过程中不断调整步长因子,不断改变权值,进而达到同时满足速度和精度的要求。对于本文而言,步长增益α/en-1应具有:初始情况下α/en-1趋近与1;随着自适应滤波器慢慢逼近有用信号,α/en-1→0。

3Matlab仿真及结果分析

根据分布式光纤测温系统的信号及噪声信号的特点,微弱的携带温度信息的反斯托克斯信号被完全掩没在噪声中。本文用s(t)=0.384×10-6τ2-1.92×10-3t+2.4模拟反斯托克斯信号,其离散化的Matlab仿真如图4(a)所示。噪声信号noise(t)是零均值,方差为1的高斯白噪声,如图2所示。原始信号xn(t)=s(t)+noise(t),将其离散化的Matlab仿真如图4(b)所示。

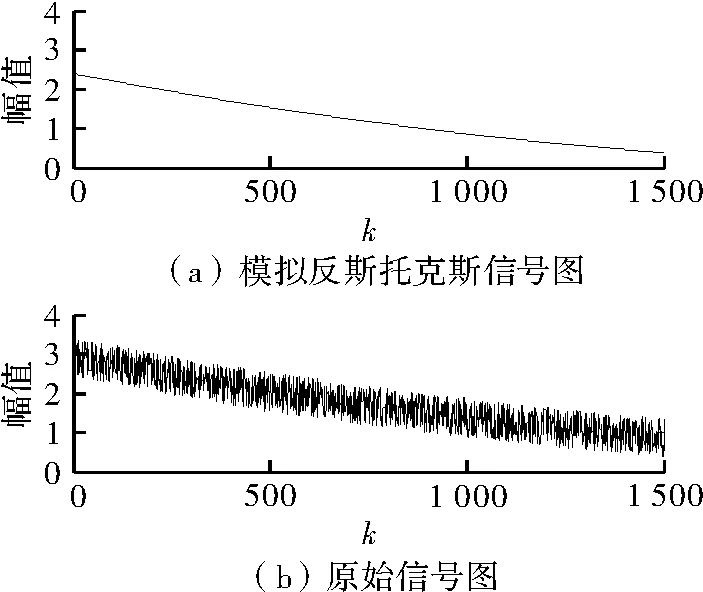
图4　Matlab仿真

研究在收敛范围内,特定噪声方差下,同一实验环境下,变步长LMS算法和固定步长LMS算法性能的比较分析以及算法稳定性、收敛速度和稳态误差大小的影响。本文经过多次仿真比较,采用计算机模拟条件:(1)自适应滤波器阶数L=5。(2)μ0=1/750,α=0.977。为得出每一条曲线,分别做500次独立的仿真,采样点数为1 500,然后求其统计平均,得出学习曲线,LMS算法的去噪效果如图5所示。统计平均的均方差信号,得到的学习曲线如图6所示。

图5是变步长LMS算法和固定步长LMS算法对分布式光纤测温温系统的原始信号的仿真结果。结果表明变步长的LMS算法与定步长LMS算法相比,滤波效果更好,稳定性和精度也更高。

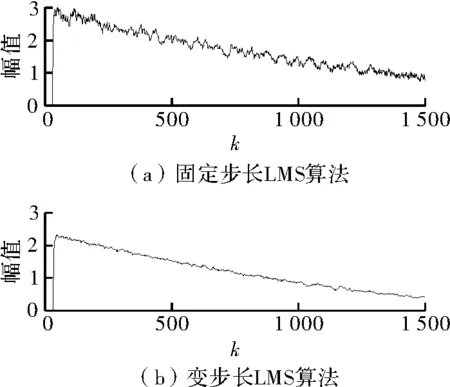
图5　LMS滤波算法去噪仿真

图6是变步长LMS算法和固定步长LMS算法的误差均方信号仿真结果。由图中可以看出,对于本文中信号的去噪收敛后稳态误差较小,变步长LMS算法在获得较小稳态误差的情况下,同时获得了比固定步长LMS算法更快的收敛速度。这是因算法在初始收敛阶段,误差值比较大,由步长调整公式可知步长值较大,因此收敛速度较快;而在算法收敛后,由于误差值较小,步长值也变小,所以拥有较小的稳态误差。

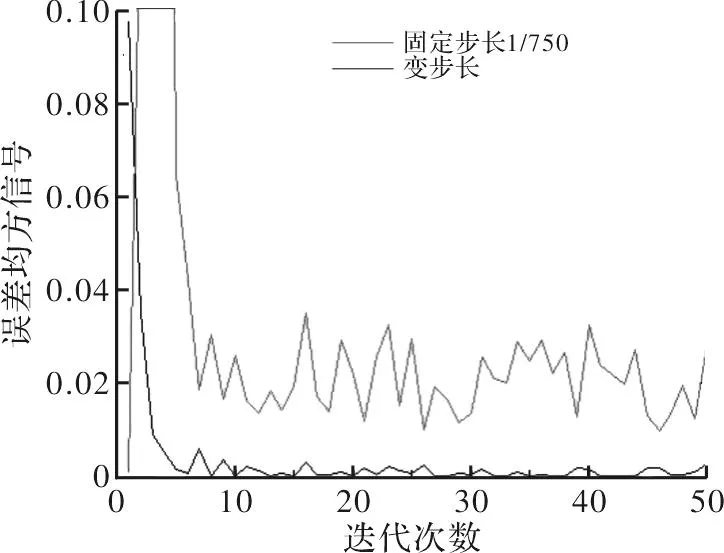
图6　LMS算法的误差均方信号

参考文献

[1]李铮.基于后向喇曼散射的分布式光纤测温系统研制[D].北京:北京航空航天大学,2008.

[2]张达伟.光纤测温系统信号处理方法的研究与实现[D].大连:大连理工大学,2008.

[3]曹立军.分布式光纤温度测量及数据处理技术研究[D].合肥:合肥工业大学,2006.

[4]HaykinS.Adaptivefiltertheory[C].4thed.Printice:Printice-Hall,2002.

[5]DirkTMSock.OntheconvergencebehavioroftheLMSandthenormalizedLMSalgorithms[J].IEEETransactionsonSignalProcessing,1993,41(9):2811-2825.

[6]沈凤麟,陈和晏.生物医学随机信号处理[M].合肥:中国科学技术大学出版社,1999.

[7]倪锦根,李锋.一种新的变步长最小均方自适应滤波算法[J].信息与电子工程,2008,6(1):10-13.

[8]罗小东,贾振红,王强.一种新的变步长LMS自适应滤波算法[J].电子学报,2006,34(6):1123-1126.

[9]杨飞飞,阴亚芳.一种新的变步长LMS自适应算法[J].电子科技,2013,26(5):125-127.

[10]曲勇.基于RMMSE的自适应算法[J].电子科技,2013,26(11):51-54.

[11]徐艳,李静.基于LMS算法与RLS算法的自适应滤波[J].电子设计工程,2012,20(12):49-51,54.