疲劳谱分析方法及其在立柱式平台结构分析中的应用

李华祥

(上海利策科技股份有限公司，上海 200233)

疲劳谱分析方法及其在立柱式平台结构分析中的应用

李华祥

(上海利策科技股份有限公司，上海 200233)

基于海洋疲劳谱分析理论，对海洋桁架型立柱式(Truss Spar)平台的疲劳强度与结构寿命进行分析计算。基于经典波浪疲劳谱理论，开发出一套针对海洋结构的疲劳谱分析程序。同时，依据Goodman理论，将平均应力对疲劳极限的影响进行修订。该疲劳程序与海洋结构有限元分析模块进行无缝连接，实现立柱式平台有限元建模、水动力载荷计算与结构映射、有限元强度计算、疲劳计算的全自动耦合。数值算例计算结果表明，对于在位工况条件桁架型立柱式平台，其结构疲劳失效关键点在硬舱与桁架交接处，这为结构的局部加强和优化设计提供重要参考。

立柱式平台；疲劳谱分析；Goodman 理论；有限元分析

0 引 言

海洋平台结构系统的工程设计包括船体设计、分析计算、规范校核三个部分。其中船体设计工作主要依据海洋工程行业规范和设计经验，对平台的结构系统进行初步方案设计。分析计算是在初步方案设计基础上，根据已确定的平台结构设计参数和海洋环境等条件，进行水动力、稳性、运动性能、结构强度、系泊强度、立管强度等分析与数值计算。规范校核则是对上述分析计算的结果，根据规范细则要求，对关键设计参数进行校核，校对平台设计的合理性和可靠性，并根据校核结果对设计提出优化和改进意见。疲劳分析及以此为基础进行的结构寿命预测，又是平台结构分析计算的一个重点。

作为一种新型海洋浮式平台，立柱式(Spar)平台的工程应用在最近十几年得到了迅猛增长。但深海恶劣的动态海洋环境条件，在结构内部产生损伤累积和裂纹扩展，进而造成结构疲劳失效，这已成为海洋平台破坏的最重要形式之一。因此，疲劳分析已成为立柱式平台结构设计的一个重点。目前，工程中多采用简化疲劳分析和疲劳谱分析方法来评估海洋平台结构的疲劳寿命[1-7]。由于疲劳谱分析基于真实海况条件进行直接计算，精度相应较高，但存在计算流程复杂、涉及水动力与有限元综合分析计算、计算量大等困难，这方面的理论研究和实用工具也仍然在发展中。

基于经典波浪疲劳谱分析理论，本文开发了一套针对海洋平台结构的疲劳谱分析计算程序，并将该程序与海洋结构有限元强度计算程序模块进行无缝连接。借助计算机辅助设计功能，完成浮式平台疲劳分析所需的系列流程工作的耦合进行。数值算例进一步显示该方法对桁架型立柱式(Truss Spar)平台的适用性和先进性。

1 疲劳谱分析方法

海洋结构的疲劳谱分析是基于真实的海况和波浪载荷条件进行直接的计算，比其他分析方法(如简化方法和确定性方法)精度高很多，所以成为海洋结构疲劳寿命预测首选方法。疲劳谱分析方法涉及复杂的水动力和有限元交互计算，基于波浪谱和疲劳-寿命(S-N)曲线的损伤度计算是疲劳谱分析的核心，该计算的流程[8-9]如下。

(1) 计算结构中某一点的应力传递函数Hσ(ω|θ)。其做法是对结构在指定的波浪频率范围和浪向角进行一系列的应力分析，得到的应力结果就可以直接用于得到该点的应力传递函数。

(2) 通过应力传递函数Hσ(ω|θ)和波浪散布图中某一短期海况的波浪谱密度函数Sη(ω|Hs,Tz)，可由下式得到应力能量谱Sσ(ω|Hs,Tz,θ)：

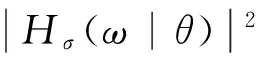
(1)

(3) 计算应力能量谱的谱矩，第n阶谱矩mn表达式为

(2)

由于大部分的疲劳损伤是由中低海况引起的，因此应该考虑短峰波的作用。短峰波会引起波浪能量的分散，这种分散可通过一个平方余弦函数加以考虑。通常，平方余弦函数假设的传播方向为与选定波浪方向成-90°～+90°夹角的范围内，也即半个平面。考虑波浪扩散函数后的谱矩公式为

(3)

(4) 应用得到的谱矩，即可计算应力范围短期分布的概率密度函数(瑞利分布)的跨零周期和带宽系数。瑞利分布概率密度函数为

(4)

跨零周期计算公式为

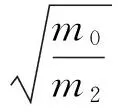
(5)

带宽系数计算公式为

(6)

(5) 应用Miner准则计算疲劳损伤累积。当某一短期海况产生的应力短期分布的概率密度函数满足瑞利分布时，那么第i个短期海况造成的短期疲劳损伤为

(7)

式中：Di为第i个短期海况造成的短期疲劳损伤；Td为设计寿命；foi为对应于跨零周期的跨零频率；pi为对应于波浪散布图的该短期海况出现的概率；gi为瑞利分布中产生应力S的概率密度；m、K为S-N曲线参数。

对波浪散布图中各个短期海况造成的损伤进行累加，就得到总的累积损伤。计算公式如下：

(8)

式中：D为计算点处总的疲劳损伤；f0为计算点在结构整个生命周期中的应力范围S的平均概率。

(6) 损伤计算解析表达式，对于两段直线的S-N曲线，在拐点(NQ，SQ)处，该S-N双直线的斜率从m变为m+Δm，常数K1变为K2，所以疲劳损伤表示为

(9)

式中：λ(m,εi)为雨流修正系数，

(10)

μi为低周疲劳损伤修正系数，

(11)

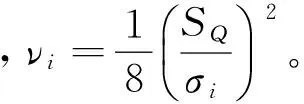
2 Goodman 疲劳方程

基于S-N曲线进行工程疲劳计算与结构寿命预测时，试验曲线均基于循环对称载荷，即σmax= -σmin，其中，σmax为材料在承受循环载荷过程中最大应力值，σmin为材料承受循环载荷过程中最小应力值。但是，对于工程结构，在复杂应力状态下，大多数受力点处循环应力为非对称应力，此时，试验曲线中的应力幅 Δσ需要作相应修订，才能反映真实应力状态下材料的疲劳极限。

不同的平均应力可用应力比R表示，其计算公式为

(12)

几种典型循环应力状态对应的应力比R分别为

(13)

对于材料S-N曲线的测试，多数基于对称应力循环状态，即R= -1。在实际运用这些S-N曲线时，还需根据不同应力状态对S-N曲线进行修订。即在结构疲劳计算时，需根据不同应力比R对结构各点的应力幅进行修订计算，然后根据修正后的应力幅，配合使用S-N曲线，获得结构各对应点的疲劳极限。

在众多的疲劳极限修订理论中，Goodman理论目前在工程中应用最为广泛。Goodman 疲劳方程可表示如下：

(14)

式中：σF为修正后的疲劳极限应力幅；σ-1为对称循环下的疲劳极限应力幅；σm为平均应力。根据平均应力和式(14)，对疲劳极限进行修正，基于修正后的疲劳曲线，计算结构受力点的损伤度和疲劳强度：

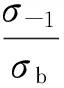
(15)

式中：ψK为平均应力影响系数；σb为材料的抗拉强度。平均应力影响系数ψK的值不仅与材料有关，同时与应力集中系数Kσ也相关。表1[8]给出钢材Q345的平均应力影响系数ψK。

在结构强度计算中，一旦各材料点的应力计算获得，根据其应力比R、平均应力σm和应力集中系数Kσ，则根据公式(15)或表1查询获得平均应力影响系数ψK。然后根据公式(14)，对疲劳极限进行修正，再根据修正后的疲劳曲线和参数，在相应的材料S-N曲线或S-N曲线方程，获得该受力点的疲劳极限循环数。结合上节理论，就可以进行结构的疲劳谱分析计算。

表1 平均应力影响系数

3 结构疲劳计算流程

结构疲劳谱计算基于结构有限元强度计算，为此首先需要进行有限元建模和水动力载荷计算，并进行水动力载荷结构映射，然后才能进行有限元强度计算。再得到结构应力计算结果，便可进行结构损伤度和疲劳谱分析计算。

3.1 有限元建模

有限元建模与分析计算基于ANSYS软件，采用APDL语言，根据目前工程桁架型立柱式平台结构形式，借助一体化集成软件系统，实现结构的有限元建模、单元划分、加载、求解、结果输出等工作。

为了提高结构建模的效率，充分利用参数化建模的特点，将桁架型立柱式结构进行拆分归类，具有相似特征的结构组合成各类子结构，其中板材为一级子结构，附着在一级子结构上的扶强材和桁材为二级子结构，最后通过计算机的循环处理实现同类结构的批量建模。例如，硬舱结构分为四类一级子结构，分别为分层甲板(Deck)、外壳板(Side Shell)、舱壁板(BHD)和中心井(Access Shaft)。对于每类一级子结构，结构形式没有变化，只有尺寸稍有差异。各子结构的尺寸参数包括板材厚度、长度、宽度等，均采用数组的形式存储，所以只需输入不同的参数便可得到不同的结构。一级子结构建模完成后，调用二级子结构参数数组，在一级子结构上建立对应的扶强材和桁材模型。软舱与中段桁架也采用类似的方式建模，再通过耦合处理完成模型的整合。结构与有限元建模的流程包括参数读入、整体几何模型、加强筋生成、单元划分和模型处理。其中，整体几何模型模块的功能是根据输入的参数生成一级子结构；加强筋生成模块的任务是根据参数在一级子结构上生成二级子结构；单元划分模块通过参数控制将平台划分成高质量的四边形单元；模型处理模块的功能是对模型进行对称、复制以及合并等操作。

3.2 水动力载荷结构映射

参数化建模模块的目标是得到桁架型立柱式平台的结构与有限元模型(见图1)，同时基于有限元模型和平台设计参数(如吃水、重量、中心位置、水动力等参数)，自动产生平台的水动力模型(见图2)。本文水动力模型不包括中段桁架结构，桁架结构受到的波浪载荷通过Morison公式计算得到，然后直接加载到有限元模型上。

图1 有限元模型示意图Fig.1 Diagram of finite element model

图2 水动力模型示意图Fig.2 Diagram of hydrodynamic model

立柱式平台所受载荷可以分为两类：静态载荷与环境载荷。其中，静态载荷包括平台重量、压载重量、作业载荷和浮力；环境载荷包括风载荷、流载荷以及波浪载荷，其中波浪载荷根据波浪散布图的短期海况条件分别计算。考虑桁架型立柱式平台近似轴对称，为了简化全结构映射计算量，浪向角仅计算0°。

水动力载荷计算，使用AQWA软件读入水动力模型，利用AQWA-LINE根据势流理论计算出水动力模型的波浪力数据，最后通过AQWA-WAVE生成针对有限元模型的波浪载荷数据，该数据符合ANSYS APDL语言的格式要求。所以在ANSYS软件平台上直接读入上述波浪载荷数据，即可完成水动力载荷到有限元模型的波浪力映射。

3.3 有限元建模

在水动力载荷加载基础上，还需同时加载其他类型载荷，如风载荷、流载、自重、浮力等。本文对风速和流速采用百年一遇的海况条件进行加载，由于未建上部组块的模型，风载荷等效为均布力与弯矩施加在硬舱顶部，流载荷则以压力形式加载在对应位置。

3.4 疲劳谱计算

在有限元分析计算基础上，按照上述疲劳分析计算流程便可计算平台结构各节点的疲劳损伤度。本文波浪波谱采用JONSWAP谱形式：

(16)

水面以上结构S-N曲线采用ABS的A-E曲线，水下结构S-N曲线采用美国船级社(ABS)的CP-E曲线。具体S-N曲线参数如表2所示。

本文采用挪威船级社(DNV)世界海域通用波浪散布图[10]数据进行疲劳计算。该波浪散布图数据如表3所示。

表2 疲劳分析S-N曲线参数

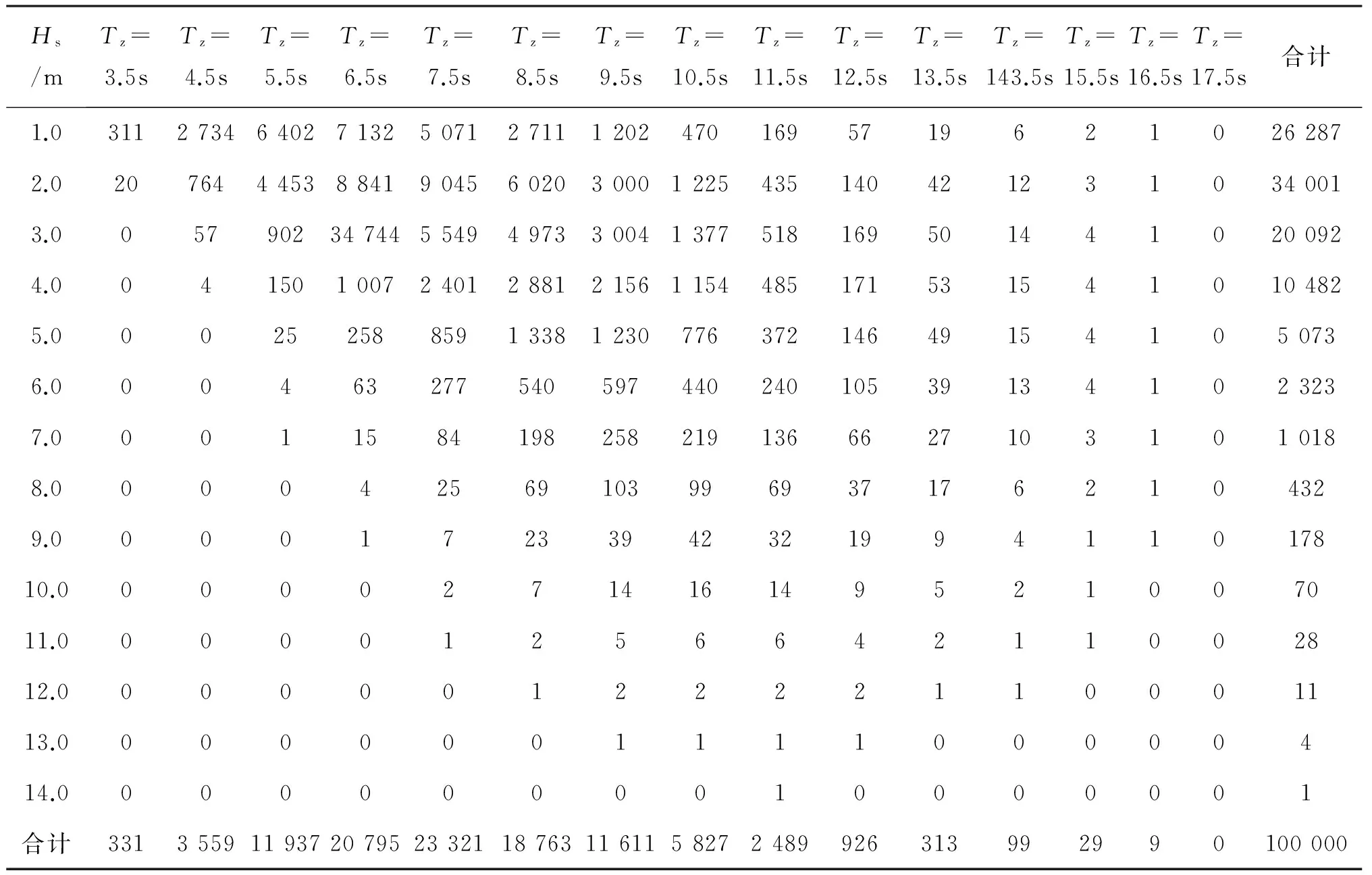
表3 波浪散布图数据

4 算 例

基于该集成软件系统，对某项目桁架型立柱式平台进行疲劳谱分析计算。针对该项目平台作用海域条件和设计条件，在集成软件系统中，首先运行设计子系统获得该平台的主尺度参数和结构参数，如表4所示。

模型采用了shell181、beam188、pipe288以及mass21单元类型。弹性壳单元shell181用来模拟硬舱外壁板、中央井壁板、隔舱壁板、硬舱分层板、垂荡板、软舱外壁板以及软舱隔舱壁板等厚宽比较小的构件。梁单元beam188用来模拟附着在壳单元上的桁材和扶强材。管单元pipe288用来模拟中段桁架。质量单元mass21用来模拟压载物，这些单元在结构有加速度的作用下，会产生惯性力，使结构产生变形。

表4 平台主尺度

平台吃水深度为176 m，静载工况(见表5)包括结构自重、上部组块重量、浮力、系泊预张力、立管荷载以及压舱力。10 min内平均最大风速为33.2 m/s。流速分布如表6所示。JONSWAP谱参数γ=3.3进行波浪短期海况计算，长期海况分布见表3。

本文假定桁架型立柱式平台疲劳设计寿命为20年，则结构的疲劳UC值定义为

(17)

式中：Kf为安全系数，本文取3；Td为设计寿命，本文假定为20年；T为结构节点的计算疲劳寿命。UC=1.0表示该计算点疲劳寿命刚好满足设计要求，而若UC>1.0 则计算点疲劳寿命不满足设计要求。

运用本文方法，在不考虑平均应力对疲劳强度影响的前提下，对目标桁架型立柱式平台进行疲劳分析计算，结果如表7所示。由于软舱在各工况下的应力响应相对较小，对应的疲劳寿命也比较大。由于个别单元应力异常导致软舱的最大疲劳UC值达到0.79，实际的疲劳UC值远小于该值。根据式(17)进行疲劳UC值计算，典型结构疲劳云图见图3～9。从疲劳UC值云图可以看出，对于在位工况，桁架型立柱式平台结构疲劳失效发生在硬舱与桁架交接处。

为了计算平均应力对上述疲劳强度的影响，再次对疲劳危险节点处的疲劳寿命按本文式(14)进行修订计算。由于疲劳关键节点处也是应力集中比较明显的位置，取平均应力影响系数0.12，对硬舱、桁架、垂荡板疲劳危险节点处进行修订计算，计算结果如表8所示。从计算结果可以看出，考虑平均应力的影响，结构的疲劳寿命也大为减少。该方法将更加安全地计算结构的疲劳强度和使用寿命，可以得出海洋结构设计的重要参考数据。

表5 静态载荷数据

表6 百年一遇的流速

表7 结构疲劳UC值

表8 考虑平均应力影响的结构疲劳UC值

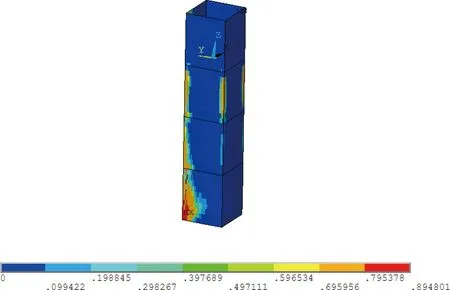
图3 硬舱中心井疲劳UC值Fig.3 Fatigue UC of the central shaft of hard tanks

图4 硬舱舱壁板疲劳UC值Fig.4 Fatigue UC of the hard tank bulkheads

图6 硬舱外板疲劳UC值Fig.6 Fatigue UC of the external plates of hard tanks

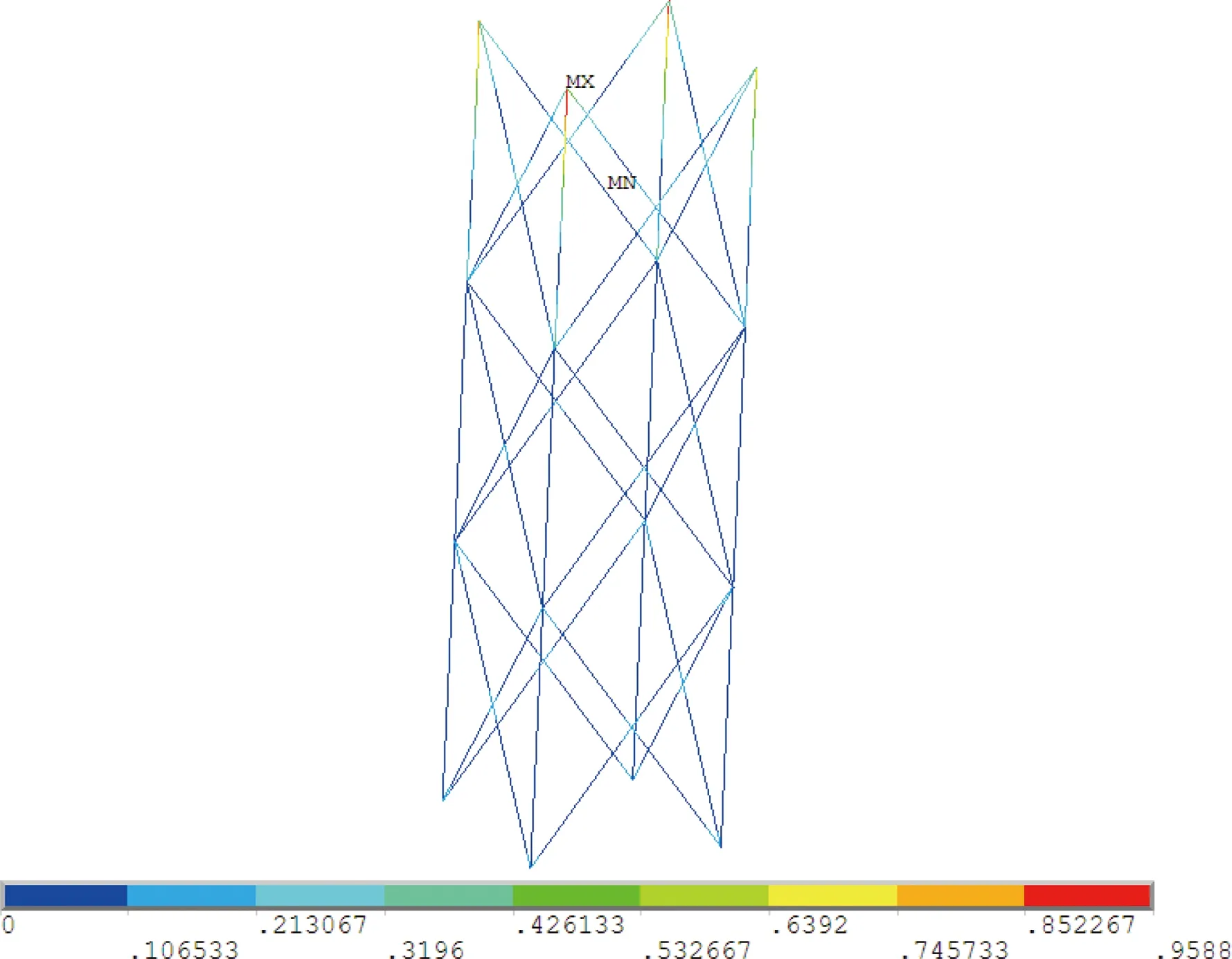
图7 桁架整体疲劳UC值Fig.7 Global fatigue UC of the truss

图8 垂荡板整体疲劳UC值Fig.8 Global fatigue UC of the heave plates

图9 软舱整体疲劳UC值Fig.9 Global fatigue UC of the soft tanks

5 结 语

本文基于疲劳谱分析理论和Goodman理论，开发了一套海洋结构物的疲劳计算与寿命预测程序，并将该方法应用到海洋桁架型立柱式平台的疲劳计算。同时将该疲劳程序与海洋结构有限元分析程序进行无缝连接，实现桁架型立柱式平台有限元建模、水动力载荷计算与结构映射、有限元强度计算、疲劳计算的全自动耦合。数值算例显示，对于在位工况，桁架型立柱式平台结构疲劳失效发生在硬舱与桁架交接处。这为结构局部加固和结构优化设计提供主要的参考。

[1] 张立，金伟良. 海洋平台结构疲劳损伤与寿命预测 [J]. 浙江大学学报(工学版)，2002，36(2): 138.

[2] 冯国庆，任慧龙. 船体结构疲劳评估的设计波法 [J]. 哈尔滨工程大学学报，2005，26(4): 430.

[3] Fricke W, Doerk O. Simplified approach to fatigue strength assessment of fillet-welded attachment ends [J]. International Journal of Fatigue, 2006, 28(2): 141.

[4] Fricke W, Kahl A. Comparison of different structural stress approaches for fatigue assessment of welded ship structures [J]. Marine Structures，2005, 18(7-8): 473.

[5] Fricke W, Cui W, Kierkegaard H. Comparative fatigue strength assessment of a structural detail in a containership using various approaches of classification societies [J]. Marine Structures, 2002, 15(1): 1.

[6] Lotsberg I, Landet E. Fatigue capacity of side longitudinal in floating structures [J]. Marine Structures, 2005, 18(1): 25.

[7] Lotsberg I. Assessment of fatigue capacity in the new bulk carrier and tanker rules [J]. Marine Structures, 2006, 19(1): 83.

[8] American Bureau of Shipping. Guide for the fatigue assessment of offshore structures [S]. 2003.

[9] American Bureau of Shipping. Commentary on the guide for the fatigue assessment of offshore structures [S]. 2004.

[10] Det Norske Veritas. DNV-RP-C205. Environmental conditions and environmental loads [S]. 2007.

[11] 闻邦椿. 疲劳强度与可靠性设计[M]. 北京: 机械工业出版社, 2016.

SpectrumFatigueAnalysisMethodwithApplicationtotheStructuralAnalysisofSparPlatforms

LI Hua-xiang

(ShanghaiRichtechEngineeringCo.,Ltd.,Shanghai200233,China)

Based on the offshore spectrum fatigue theory, this paper is to calculate the fatigue strength and life predication of truss spar platforms. By means of the classical wave spectrum theory and the engineering fatigue theory, a software tool is developed for the spectrum fatigue analysis of structures. Meanwhile, based on the Goodman theory, the effect of mean stresses on fatigue limit is evaluated. The developed software is linked with a finite element analysis tool for offshore structures. Then, the chain work of finite element modeling, hydrodynamic load calculation and mapping to structural models, finite element strength analysis, and fatigue computation is automatically implemented. Numerical examples indicate that for a truss spar platform, the fatigue failure occurs at the stressed places and the intersection of hard tank and truss, which provides an important reference for local structural reinforcement and optimization.

spar platform; spectrum fatigue analysis; Goodman theory; finite element analysis

2016-09-30

上海市优秀技术带头人项目“深海柱式平台基本设计软件系统开发”(15XD1522200)

李华祥(1971—)，男，博士，主要从事海洋浮式平台设计与高性能计算研究。《海洋工程装备与技术》编委。

U661.43

A

2095-7297(2016)06-0338-08