三轴无源稳定平台研制

2016-01-08李付军

机械与电子 2015年4期

关键词：闭环阻尼

三轴无源稳定平台研制

李付军

(中国电子科技集团公司第三十八研究所，安徽合肥 230031)

Research on Passive Stabilized Platform

LI Fujun

(NO.38 Research Institute of CETC，Hefei 230031，China)

摘要：球载雷达稳定平台主要用于隔离气球运动对雷达天线的干扰。介绍了一种基于阻尼技术的三轴无源稳定平台的设计。给出了稳定平台的原理及组成，并介绍了阻尼稳定、实时定北等关键技术。该稳定平台已成功应用于某型号系留气球载雷达系统中，工作稳定可靠。

关键词：稳定平台；阻尼；闭环

中图分类号：TN820.3

文献标识码：A

文章编号：1001-2257(2015)04-0030-03

收稿日期：2014-08-15

作者简介：李付军(1980-)，男，安徽阜阳人，硕士，高级工程师，主要从事天线伺服系统和稳定平台的研制开发。

Abstract：Stabilized platform is mainly used to separate radar from being interfered by tethered aerostat borne. The paper introduces the design of the passive stabilized platform.And also，the damp technology and north alignment technology are listed.It is proved that the control system runs stably and meets the design requirements.

Key words：stabilized platform; damp; feedback loop

0引言

系留气球载雷达稳定平台是以系留气球为搭载平台，用来搭载天线等负载。当气球升至高空后，通过稳定平台来隔离减弱气球姿态运动对负载带来的影响，同时稳定平台的控制系统通过一定的控制方式实现天线或其他负载转动、定位和扇扫等功能，实时输出天线在大地坐标系下的北向角和稳定平台的状态。

1稳定平台工作原理及组成

稳定平台按稳定方式分为有源稳定和无源稳定。有源稳定平台是一种由控制系统检测外部扰动、并驱动执行机构实现所搭载的负载在惯性空间内指向稳定的伺服系统，能有效隔离运动载体因姿态变化带来的扰动，保证负载指向的稳定。无源稳定方式即利用雷达设备自身重力，选择合适的阻尼形式和结构，实现在规定时间内达到水平稳定精度的调整目标。稳定平台按照结构型式分为单轴、两轴和三轴稳定平台。

该系统中稳定平台负载惯量较大、反应速度与稳定精度要求不高，具有体积小、重量轻的要求，同时需隔离气球横滚、俯仰和航向3个方向的姿态角运动，最终确定采用基于阻尼技术的无源三轴稳定平台，实现了重量轻、结构简单紧凑、控制系统简单。

基于阻尼技术的三轴无源稳定平台主要由十字轴稳定平台、控制分机、光纤陀螺罗经和开关电源4个部分组成。方位驱动采用直流电机加减速器的驱动型式，通过小齿轮带动大齿轮驱动天线运动，控制分机是稳定平台控制核心，实现天线的运动控制及状态采集，光纤陀螺罗经用以实时采集稳定平台的北向角信息。稳定平台系统组成如图1所示。

图1　稳定平台系统组成

2关键技术问题的分析与解决

2.1十字联轴、四阻尼杆无源被动稳定

基于对重量和体积的限制，系统采用十字联轴节悬挂承载结构技术。异面垂直的十字联轴节联接动机座和定基座，组成二自由度承力框架结构，两轴异面垂直布置，最大限度降低结构件的尺寸和重量。四根阻尼器通过铰接的方式在动基座和定基座之间对称布置。

鉴于球载雷达载体低频运动的特点，系统选用了活塞式粘滞流体阻尼器作为耗能装置，粘滞流体阻尼器是一种无刚度的速度相关型阻尼器，即在一定的低频工作范围内，阻尼器的阻尼力与活塞的运动速度近似呈线性关系。

活塞式粘滞流体阻尼器主要由缸筒、活塞、阻尼材料、密封件和连接铰链等部分组成。活塞上设计有阻尼孔，缸筒空腔内装满半流体高分子化合物作为阻尼介质。阻尼器结构如图2所示。

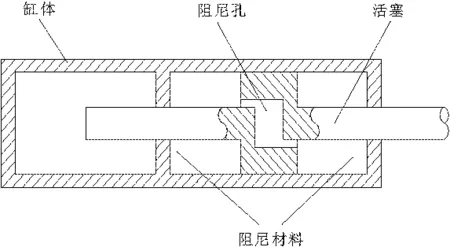
图2　阻尼器结构原理

在气球姿态发生运动变化时，4根阻尼器会依靠搭载的天线、电子机架等负载的重力，通过连接铰链带动活塞与缸筒之间发生相对运动。由于活塞两侧的压力差使半流体阻尼材料从阻尼孔中通过，阻尼材料流动时与阻尼孔产生粘滞阻力，将机械能迅速转化为热能并释放，达到耗能与缓冲作用，保证搭载天线水平方向的稳定。

阻尼器的设计内容主要为阻尼参数计算与结构设计。

阻尼力大小主要与活塞有效面积、阻尼孔结构型式与尺寸、活塞运动速度、阻尼材料等因素有关。

根据球载雷达的应用特点及阻尼力学公式，阻尼器的阻尼参数计算方法一般为:

a.根据气球姿态变化情况，分析计算出天线因此而产生的机械能。

b.根据能量守恒原理，计算出能量转化过程中需要阻尼力F的大小。

c.根据天线的机械能转换情况，计算出活塞的运动速度V。

d.根据阻尼介质特性得出系数α，并根据公式计算出阻尼常数c。

根据上述计算结果进行阻尼器的结构设计，最后经过一系列的试验与调试，得到符合技术要求的粘滞流体阻尼器产品。

2.2基于TMS320F28335的高精稳定平台控制系统

稳定平台控制系统是稳定平台的控制核心，系统选用DSP芯片TMS320F28335作为处理器，其具有处理功能强大，运算速度快，外围接口资源丰富等特点。以TMS320F28335为核心，扩展R/D变换器用以采集旋转变压器角度信息，TMS320F28335产生PWM信号，经专用功率放大器MSK4205,实现对直流电机的控制、A/D转换等功能。稳定平台控制系统如图3所示。

图3　稳定平台控制系统

控制系统设计采用旋转变压器检测位置构成位置闭环，测速机和光纤陀螺罗经构成双速度闭环串级控制体系，测速机构成速度内环，“空间测速机”光纤陀螺罗经构成速度外环。内环调节器主要用于消除摩擦力矩和控制对象非线性的影响；外环控制器主要用于隔离载体扰动，双环体系分层实现速度稳定环抑制内部摩擦力矩干扰和隔离球体姿态扰动的功能，软件采用分段PID逼近算法，大幅提高了动态补偿精度，动态精度可达0.1°。

2.3基于光纤陀螺罗经的动态高精度实时定北技术

为实现大地坐标系下的高精度方位角的实时输出，系统采用基于高精度光纤陀螺罗经和旋转变压器构成的“动+静”组合姿态输出方式。光纤陀螺罗经安装在稳定平台的动基座上，用于实时敏感气球的姿态角，包括航向角、横滚角和俯仰角等，旋转变压器用于检测天线相对于稳定平台静机座的相对角运动，二者数值经过一定的算法叠加运算即可得出雷达天线的实时方位角。

此外，系统需输出天线的实时指向角。因光纤陀螺罗经安装在稳定平台动基座上，不能直接检测天线的仰角，所以控制系统运算时，通过陀螺罗经输出的稳定平台横滚角、俯仰角、航向角和天线方位角，经过坐标转换及运算推导出对应方位上的波束指向角。坐标转化如图4所示。X轴方向与陀螺罗经输出俯仰方向一致，对应的Y轴为陀螺罗经输出横滚方向。OA为所要计算的方位上所作直线；∠BOA为方位角与航向角差值，定义为θ；∠AOA′为所要求的仰角，定义为γ0；γ1，γ2为对应时刻的俯仰角和横滚角。以O为极坐标圆心，建立极坐标方程，经过推导计算得出如下公式：

γ=arctan(tanγ1cosθ+tanγ2sinθ)

图4　坐标转化示意

3稳定精度试验结果

基于阻尼技术的三轴无源稳定平台，经过试验验证达到了隔离气球姿态角的要求，同时控制系统实现了对天线转速的精确控制。风速影响气球的俯仰角，风向影响气球的横滚角，气球的横滚角和俯仰角直接影响稳定平台的横滚角和俯仰角。图5为选取的气球横滚角与稳定平台的横滚角对应关系，其中横轴是时间刻度轴，记录的时间段为10点至11点，纵轴分别表示在给定时间段内的稳定平台的横滚角和气球横滚角。由图5可知，稳定平台响应曲线与气球姿态一致，满足了设计要求。通过双速度闭环的控制策略，有效地将转速误差控制在给定的范围内。