一类映射连续点集的结构
2016-01-08蒲斌斌
一类映射连续点集的结构
蒲 斌 斌
(陇西县首阳中学,甘肃 定西 748106)
摘要:基于Riemann函数的连续性及(0,1)∩Q的结构,以度量空间的开子集为全集,研究开度量空间到度量空间映射的连续点集结构,得到开集(X,d)到(Y,d1)的映射T的连续点集是(X,d)中的Gδ型集;若T定义在Rn中有内点的子集I上,以I的任意内点的一邻域为全集,根据Baire定理反证得出I∩Qn不是I中的Gδ型集,进而得到映射T不可能仅在I∩Qn上连续。
关键词:连续点;映射;Gδ型集;内点;有理点
中图分类号:O 174
基金项目:安徽省高等学校省级自然科学研究重点
作者简介:盛魁(1981-),男,安徽涡阳人,讲师,硕士,主要从事数据挖掘、智能信息检索和电子商务研究。
Structure of Continuous Points Set of a Class of Mapping
PU Bin-bin
(Shouyang Middle School in Longxi County,Dingxi,Gansu 748106,China)
Abstract:Based on the continuity of Riemann function and the structure of(0,1)∩Q,the paper defines the open subset of a metric space as complete set.By researching the set structure of continuous points of mapping from open space of metric space to the metric space mapping,we obtain that the set of continuous points of the mapping named T from open settois a set(X,d) to(Y,d1)is a set of Gδ type on(X,d);if the T is defined on I⊂Rn with interior points,which is impossible only to be continuous on I∩Qn.And defining complete set point on I a neighborhood of interior point on I,accoeding to the Baire theorem we prove that I∩Qn is not the Gδ-type set on I,and then we get:the T is impossible only to be continuous on I∩Qn.
Key words:continuous point;mapping;set of Gδtype;interior point;rational point
1引言
Riemann函数
仅在(0,1)Q上连续。
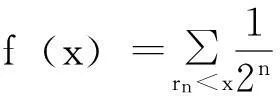
根据f(x)、R(x)的连续性,试问:是否存在仅在Q的子集上连续的函数?或者更一般的,是否存在仅在Q的子集上连续的映射?
在文献中,王家军证明了f:R→R不可能在Q上连续,在RQ上间断;在文献中,张庚尧得出定义在度量空间中开集内的实函数的连续点集是f定义域中的Gδ型集。在文献中,刘立明得出Rn上第一类Baire函数的连续点集是Rn中的第二纲集。基于文献、、的研究成果,试问:定义在一般度量空间上的函数和映射的连续点集结构是怎样的?在怎样的条件下映射的连续点集是其定义域中的Gδ型集?为了回答这些很有意思的问题,不妨先从应用范围最广泛的开度量空间(X,d)入手研究,这样或许能得出一些有用的结论。为了使叙述合理、简洁,先引入必要的定义及一些记法。
2定义
定义1设T:(X,d)→(Y,d1)是两度量空间间的映射,对∀x0∈X,若x0为T的连续点,则对∀ε>0,∃δ>0,使得T(U(x0,δ))⊂U((Tx0,ε))。
定义2设X是度量空间,M是X的子集,若M是X中至多可数个疏朗集之并,则称M是第一纲集,不是第一纲集的集合称为第二纲集。
设(X,d)为开度量空间,若T为(X,d)到度量空间的(Y,d1)的映射,用C(T)表示T的连续点集,用D(T)表示T的非连续点集。下文通过对D(T),C(T)的结构研究,得到了几个结论。首先引入几个必要的引理。
3引理
引理1设G为度量空间(X,d)中的开集,f:G→R为实函数,则f的连续点集是X中的Gδ型集。
引理2有理点集Qn是Rn中的Fσ型集,不是Rn中Gδ型集。
引理3不存在定义在Rn上的实函数f,使得f在有理点集Qn上连续,而在(Qn)c上间断。
引理4[4,5](Baire定理)若X是非空完备度量空间,则X是第二纲集;完备度量空间中的任何一个非空开集都是第二纲集。
下文对引理1、引理2和引理3进行推广,得到更一般的结果。
4结论及证明
首先推广引理1,即:
定理1设T为开集(X,d)到(Y,d1)的映射,则映射T的连续点集是(X,d)中的Gδ型集。
证明∀x0∈X,对任意的x,y∈U(x,δ),令
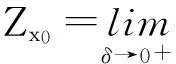
先证Zx0>0的充要条件是x0为T的不连续点。
若x0为T的不连续点,则对∀δ>0,∃ε0>0,y0∈U(x,δ),使得d1(Tx0,Ty0)≥ε0>0,即supd1(Tx,Ty)≥ε0。根据上确界的定义得,当δ→0+时,Zx单调递减,则Zx0≥ε0>0。
另一方面,若Zx0>0,则∃η>0,当0<δ<η时,存在x1,y0∈U(x0,δ),使得
Zx0≥d1(Tx1,Ty0)≥α>0
假设x0为T的连续点,则对任意的x,y∈U(x0,δ),当δ→0+时,有
即Zx0=0。这与Zx0>0矛盾,所以x0为T的不连续点。充要性得证。
于是可将D(T)分解为
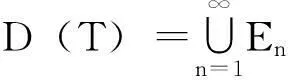
下证En为闭集。
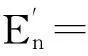
U(ν,δ1)⊂X,且∃y1∈(U(ν,δ1)∩En)
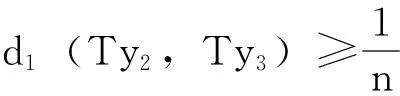
根据De Morgan公式得
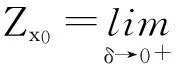
依据引理2,可对Qn的非空子集的结构进行探讨,不妨从定理1出发,对Rn的非空开子集I中的有理点I∩Qn的结构进行研究,即得如下结果:
定理2设I⊂Rn且I为开集,则I∩Qn是S中的Fσ型集,不是S中的Gδ型集。(其中I⊂S⊂Rn,且S为开集)。
证明由于Q为可数集,则Qn为可数集,所以I∩Qn至多可列。由于
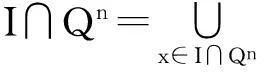
所以,I∩Qn为一列无内点闭集之并,所以I∩Qn是S中的Fσ型集。
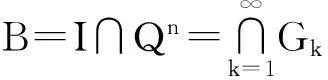
由于I∩Gk是开集,则
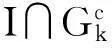
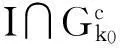
则U(x0,δ)∩Qn=Ø。这与有理数集的稠密性矛盾,所以I∩Gk为一列无内点的闭集之并。由于无内点的闭集是疏朗集,所以
为S中一列疏朗集之并。所以I为第一纲集(上述叙述中,全集为S)。又I为Rn的非空子集,根据Baire定理得I为第二纲集,矛盾。所以I∩Qn不是Gδ型集。综上所述,得证。
那么,根据已得的结论定理1和定理2,研究实映射连续点集的结构,也就是推广引理3,即得如下结论:
定理3设映射T:I→(X,d),若I⊂Rn,且I为开集,则T不可能在I∩Qn上连续,在IQn上不连续。
那么,定理3的限制条件I为开集是否还能够减弱呢?根据映射连续性的逐点定义,不妨把I为开集的条件减弱为I有内点,即:
定理4设映射T:I→(X,d),若I⊂Rn,且I有内点,则T不可能仅在I∩Qn上连续。
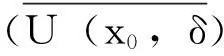
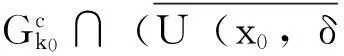
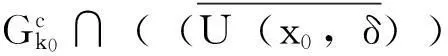
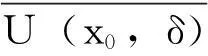
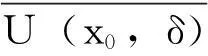
假设映射T仅在I∩n上连续,则映射T在U(x0,δ)内仅在B上连续,由定理2得,B不是U(x0,δ)内的Gδ型集。矛盾,所以映射T不可能仅在I∩Qn上连续。得证。
由于函数f(x)=c(x∈(0,1)∩Q)的连续点集是(0,1)∩Q,根据定理2可得,(0,1)∩Q不是(0,1)中的Gδ型集。所以,定理1的限制条件(X,d)是开集,定理4的限制条件I有内点已经是最弱的条件了,不能再减弱了。
根据Baire定理,可以用定理4中反证Qn∩U(x0,δ)不是U(x0,δ)中的Gδ型集的方法证明定理2,也可以用证明定理2的方法反证定理4中Qn∩U(x0,δ)不是U(x0,δ)中的Gδ型集。在此不再作重复叙述。
根据定理4,若T的定义域为R的子集,用(a,b)表示任意区间,可得到如下推论:
推论1设映射T:I→(X,d),I⊂Rn,若I有内点,则T的连续点集不可能仅为I中的有理点;任意区间(a,b)上不存在仅在其有理子集上连续的映射T。
证明假设T在I∩Q上连续,在IQ上间断。设x0为I的内点,则存在U(x0,δ)⊂I,使得T在U(x0,δ)∩Q上连续,在U(x0,δ)Q上间断。由于U(x0,δ)为开集,根据定理1得T在U(x0,δ)内的连续点集是U(x0,δ)中的Gδ型集,由定理2得,Q∩U(x0,δ)不是Gδ型集。矛盾,假设不成立。所以T不可能在Q∩U(x0,δ)上连续,在U(x0,δ)Q上间断。所以T不可能在I∩Q上连续,在IQ上间断。
由于任意区间(a,b)都有内点,由上所述,T不可能在(a,b)∩Q上连续,在(a,b)Q上间断。综上,得证。
推论2设f:U→V的函数,若U有内点,V⊂R,则f不可能仅在U中有理点连续;任意区间(a,b)上不存在仅在其有理子集上连续的函数。
推论3设f:U→V的函数,若U有内点,V⊂R,则f不可能仅在U中有理点连续;任意区间(a,b)上不存在在(a,b)∩Q上连续,在(a,b)Q上间断的实函数。
根据证明推论1的方法容易证明推论2、推论3;也可以根据定理4直接得到上述推论。
根据上文的结论,对引言中的问题可得到这样的回答:若T为开度量空间到可度量空间的映射,则T的连续点集是Gδ型集。但若T定义在一般的度量空间上,T的连续点集的结构还是不能确定。
若T定义在Rn中有内点的子集I上,则T不可能仅在I∩Qn上连续;对于Riemann函数的反面情形,有如下叙述:定义在R中有内点的子集上的函数,不可能仅在其有理子集上连续;定义在任意区间(a,b)上的函数不可能仅在(a,b)∩Q上连续。但存在定义在(0,1)∩Q上的函数仅在(0,1)∩Q上连续,如f(x)=0(x∈(0,1)∩Q)。
参考文献:
[1]王家军.实函数间断点集的结构.高等数学研究,2012,15(01):53-54.
[2]张庚尧.实函数连续点集的结构.数学理论与应用,2004,24(03):75-77.
[3]刘立明.第一类Baire函数的一个注记.广西师范学院学报:自然科学版,2006,23(02):5-7.
[4]程其襄,张奠宙,魏国强,等.实变函数函数与泛函分析基础.3版.北京:高等教育出版社,2010:191-282.
[5]熊金城.点集拓扑讲义.4版.北京:高等教育出版社,2010:247.
[6]陈海燕,戴牧明.A Note of a class ofGδsets..四川大学学报:自然科学版,2005,42(01):19-22.
[责任编辑:郑秀亮英文编辑:刘彦哲]
