箱涵施工分层填筑过程的三维有限元模拟

箱涵施工分层填筑过程的三维有限元模拟

主要研究结构设计及岩土工程。

王志鹏1，伍韵莹2，宁克明1

(1.中国市政工程西北设计研究院有限公司深圳分院，广东 深圳 518048；2.广东省水利电力勘测设计研究院，广州 510635)

摘要：在ABAQUS有限元软件的基础上，先建立箱涵的三维实体模型，再运用其多步分析和生死单元功能，对箱涵的施工填筑过程进行模拟。文中对箱涵的分层计算和整体计算结果进行了对比，对比结果表明：在仅考虑混凝土弹性性质的基础上，合理地模拟施工填筑过程时，箱涵的应力和位移均大于整体计算结果的10%左右。考虑到计算方法的复杂性和工程应用中的适用性，仅建议在复杂和重要的工程中，对箱涵的施工填筑过程进行模拟。

关键词：箱涵；ABAQUS；施工分层填筑；数值模拟

0引言

近年来，随着基础设施建设规模的不断加大，箱涵这类填埋式构筑物，被广泛地运用在水利、交通、市政等工程中，其施工过程包括基坑开挖、主体结构浇筑以及上覆土体的回填。目前，对这类构筑物的基坑开挖、箱涵与土体相互作用和箱涵结构的受力特征方面的研究较多，而对箱涵施工的全过程的研究较少[1]，但是与箱涵的完建期相比，箱涵在施工过程中的内力和变形是很复杂的，很难确定箱涵的最不利工况。另一方面，在箱涵的各种作用荷载中,回填土体压力与地面荷载可占总作用力的60%左右,尤其是对于无压箱涵，其影响更为突出，因此，在工程设计中准确地分析土压力的作用和规律,具有重要的理论和工程应用价值[2]。

箱涵的受力计算方法包括传统的结构力学方法和有限单元法等。传统的结构力学方法虽然计算方便、节省时间，在各种设计方法高速发展的今天依旧被广泛地应用，但是没有考虑箱涵施工过程的影响，不能全面地反映箱涵的内力和变形状态；而有限单元法作为当今工程分析中被最广泛应用的数值方法，由于它的通用性和有效性，受到了工程技术界的高度重视，已经成为计算机辅助工程和数值仿真的重要组成部分，能够较全面准确地反映工程的实际情况。

为了能较准确地找到箱涵的最不利工况，必须对箱涵分层填筑的施工过程进行合理的模拟，本文基于此，现借助于ABAQUS有限元软件平台进行模拟计算。

1计算原理

1.1整体计算原理

所谓的整体计算是假定在瞬间将全部荷载(此处指重力荷载)施加到整个结构上，而不考虑实际施工中荷载的逐级施加。

1.2分层计算原理

分层计算可以模拟箱涵的施工过程，其所承受的土体压力是逐层施加到结构上的，各层填土的自重仅对前期的填土层有影响，而对后续填土层无影响。模拟施工分层的填筑过程，可正确地反映施工分层加载作用与被作用关系，使计算结果更贴近实际情况；另一方面，模拟施工分层加载过程也适应非线性应力应变模型增量法计算的要求。

1.3整体计算与分层计算的比较[3]

文献[3]用图1中的(a)和(b)来分别表示整体计算和分层计算的作用机理。

图1(a)中整个结构是在填筑完成后才能形成的，将其分成上、中、下3层计算单元网格，整体计算时所有荷载由这3层网格共同承担，这样一来，不管填土的先后次序如何，上层那些本是后来填筑形成的网格的应力分布和变形，都要受到下部填土自重的影响。而在图1(b)中，某一层竣工后，只有已填筑的那部分土体(即该层及其以下各层)来承担荷载，对当时尚不存在的上层各单元网格是无影响的。

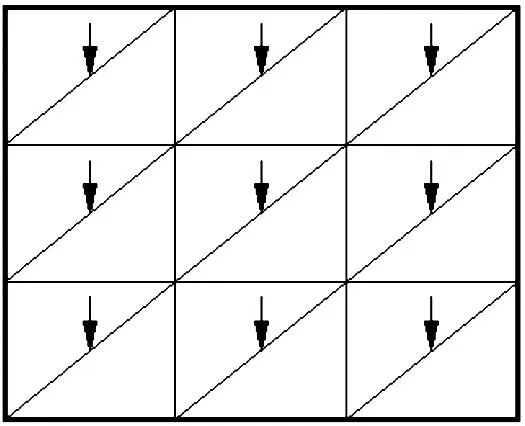
(a)

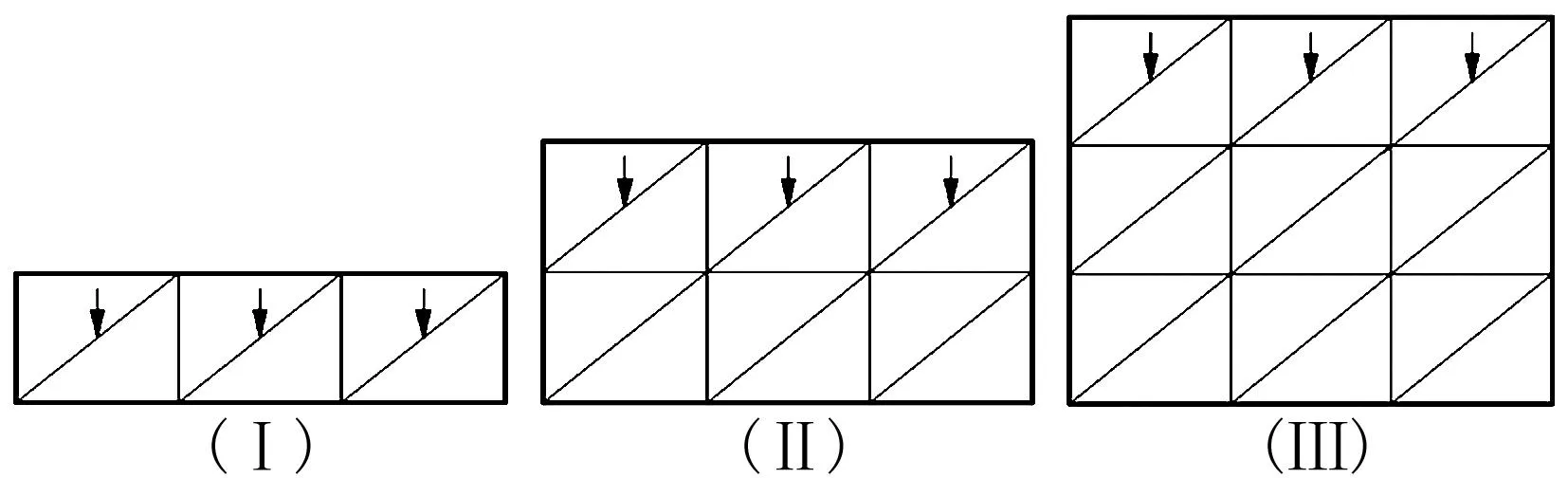
(b)图1　整体计算与分层计算示意图

1.4有限元软件的模拟原理

有限元软件模拟分析是通过逐级增加计算域内的单元数目来模拟逐层填筑过程的，通过每级新增单元的自重荷载作用，计算相应的位移增量、应变应力增量，并逐级累加，最终确定施工完成时刻的应力应变场。在这种模拟分析中按每次加载变形的最终效果进行模拟，变形按加载作用后瞬间完成。

ABAQUS有限元软件中，需要将完整的模拟加载过程划分成一些步骤，每一步骤都是用户指定的一段“时间”，在这段时间中，软件计算该模型对一组特别的荷载和边界条件的响应[4]。每一个一般步骤都是将上一个一般步骤结束时的变形状态作为起始点的，因此，模型的状态是在一系列的一般步骤中随着其对每一个步骤中所定义的载荷的响应而演化的。基于上述原理，ABAQUS软件提供的多步骤分析功能对于分步施工的工法模拟非常方便。箱涵的多步施工涉及到开挖回填断面的生死，*MODEL CHANGE、REMOVE、ADD指令能提供这种功能，使模型中被选定的单元杀死或激活。一旦单元被杀死，作用在单元上的分布力等随之处于不活跃状态，当单元被激活时，此时的分布力等随之发挥作用[5]。

2实例分析

2.1构筑单元的思路

在有限元分析中，网格的剖分直接影响结果的精度，但过密的网格又使得计算时间过长。为了更好地反应箱涵混凝土的受力状况，本模型采用能反映混凝土性质的块体单元，即三维模型进行求解。根据计算精度要求，结合所用计算机配置，本次在划分网格时,顶板、底板和侧墙上沿厚度方向分为3层网格,每层厚度为15 cm，地基及回填土的网格尺寸结合箱涵的网格进行总体划分，无限制时单元尺寸为0.8 m左右，整个模型沿轴向每隔1 m划分一层单元。

2.2计算模型简介

本次有限元计算模型是以单孔6 m×4 m箱涵的施工过程为依据建立的，箱涵的壁厚为0.45 m，覆土厚度为2 m，垫层厚度为0.1 m，箱涵、垫层、开挖沟槽、覆土为模型的主体部分。模型以箱涵为中心向两侧及下方各取2倍箱涵尺寸作为计算模型的边界，模型沿轴向的长度取10 m。三维模型以六面体单元为主，四面体单元为辅，共有单元20 580个，节点23 969个。计算模型如图2～3。

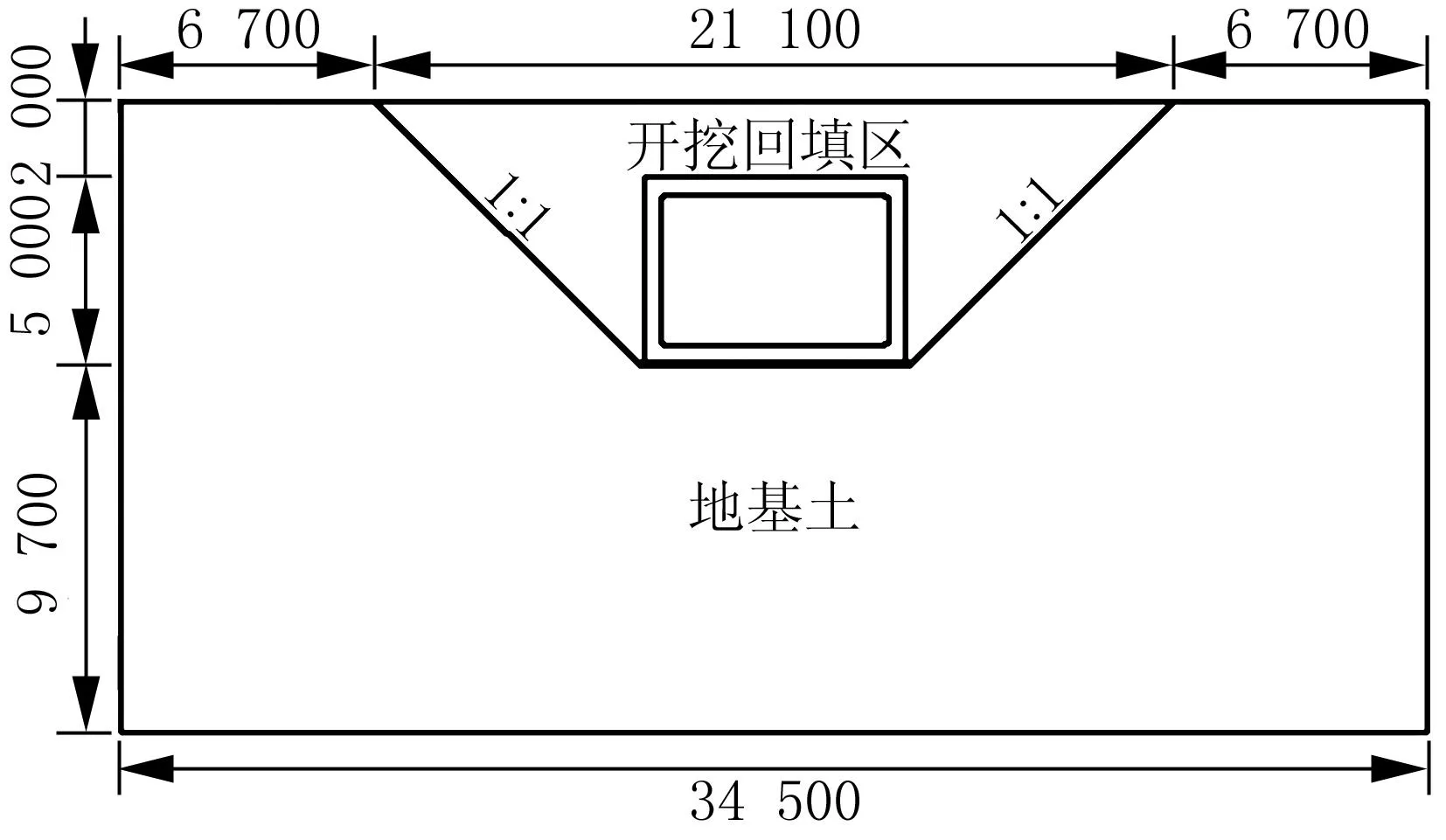
(a)结构与土的计算区域

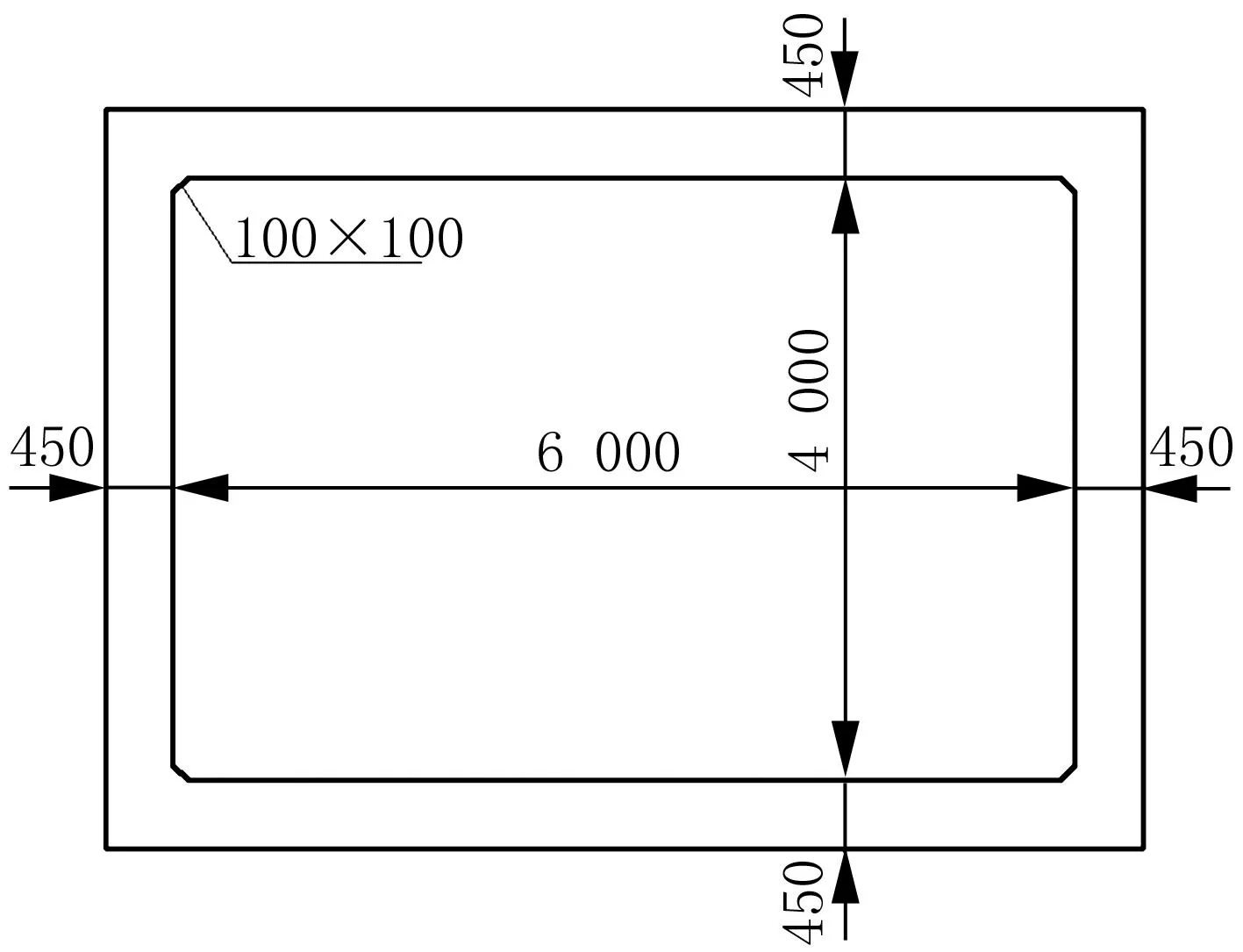
(b)箱涵结构横截面图图2　计算区域横截面示意图/mm

图3　有限元计算网格示意图

2.3计算数据

计算数据见表1。

表1　材料物理力学参数表

2.4计算成果分析及措施

本次模型计算，混凝土材料采用弹性模型，不考虑混凝土的塑性，地基及回填土采用Mohr-Coulomb材料模型。

本文采用3种工况进行计算，即：整体计算、一次分步计算和多次分步计算。整体计算相当于完建期工况，多步分析计算相当于施工期工况，而一次分步计算是介于两者之间的一种虚拟工况。现分别对箱涵计算成果中的最大主应力、等效压应力和竖向位移进行分析。在成果分析中，应力和位移的正负号采用以下规定：对于最大主应力采用弹性力学中的规定，即以拉为正，压为负；等效压应力中，以压为正，拉为负；竖向位移以竖直向上为正，竖直向下为负。

本文中整体计算是指箱涵和回填土一次加载完成；一次分步计算是指箱涵完成后，回填土一次加载完成；多次分步计算是指箱涵完成后，回填土分多次加载完成，本模型中分层厚度为0.6 m左右，共分11次加载完成。

2.4.1最大主应力成果及分析

利用最大主应力可以判断混凝土的开裂与否，即最大主应力(拉应力)大于混凝土的抗拉强度时，则认为混凝土开裂，本次计算中箱涵混凝土的轴心抗拉强度设计值为1.43 MPa。

箱涵结构在图4中(a)、(b)、(c)3种情况下所受到的最大主应力最大值依次为：3.12 MPa、3.50 MPa和3.44 MPa，整体计算结果最小，一次分步计算结果最大，三者都大于混凝土轴心抗拉强度设计值，而多次分步计算结果比整体计算结果最大值大10.3%，比一次分步计算结果最大值小1.7%。从应力云图的分布上看，3种情况的开裂区域(最大主应力大于抗拉强度)发生部位基本相同，顶板位于下侧中部，底板位于上侧中部，侧墙位于底端外侧，顶板和底板的开裂区域3种情况基本相当，但整体计算结果的侧墙开裂区域小于一次分步和多次分步计算结果。

(a)整体计算

(b)一次分步计算

(c)多次分步计算图4　最大主应力分布云图/Pa

2.4.2等效压应力成果及分析

ABAQUS中的等效压应力(Pressure)(负值时为拉应力)在一定程度上也可以反应混凝土的开裂与否，当一点的等效压应力达到一定数值时，可以认为混凝开裂，本文提供等效压应力是为了验证最大主应力分布的可靠性。

(a)整体计算

(b)一次分步计算

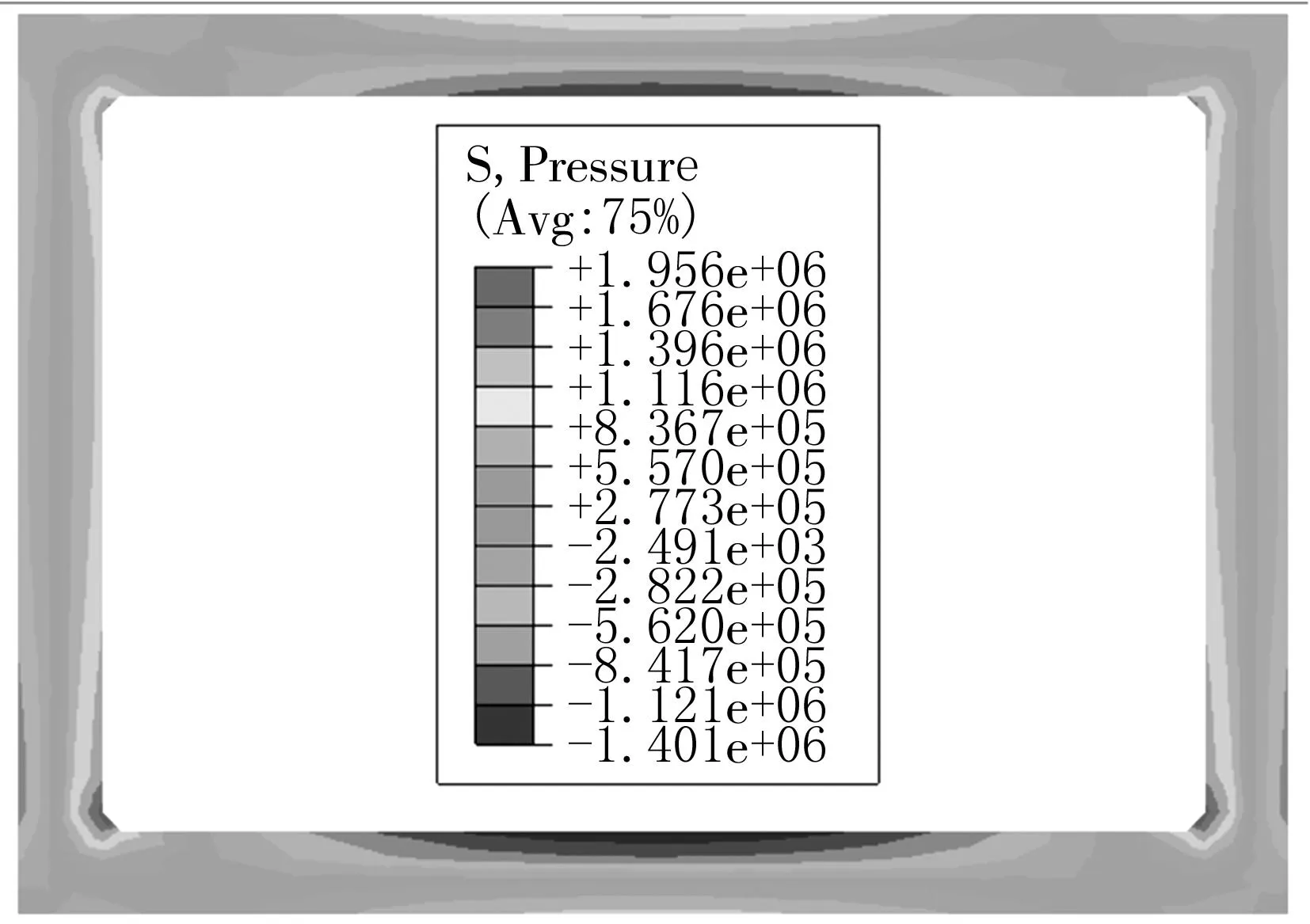
(c)多次分步计算图5　等效压应力分布云图/Pa

箱涵结构在图5中(a)、(b)、(c)3种情况下所受到的等效压应力(负值表示等效拉应力)最大值依次为：-1.25 MPa、-1.40 MPa和-1.38 MPa，整体计算结果最小，一次分步计算结果最大，三者都小于混凝土轴心抗拉强度设计值，而多次分步计算结果比整体计算结果最大值大10.4%，比一次分步计算结果最大值小1.4%。

从应力云图的分布上看，3种情况的拉应力较大区域发生部位基本相同，顶板位于下侧中部，底板位于上侧中部，侧墙位于底端外侧，三者的区域基本相同，顶、底板区域大一些，侧墙区域很小，基本可以忽略。因此，等效压应力分布与最大主应力分布的区域基本上是一致的。

2.4.3竖向位移成果及分析

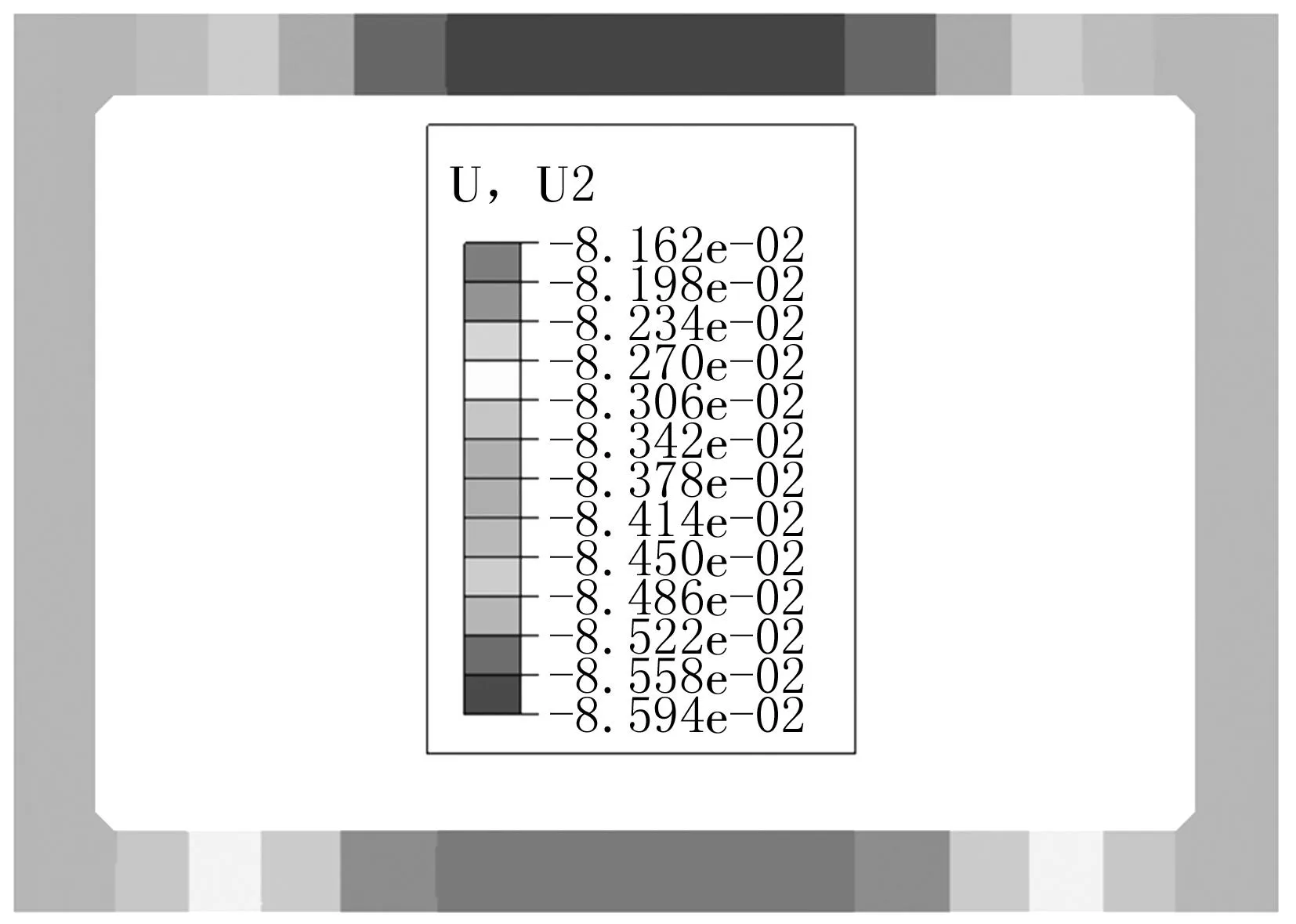
(a)整体计算

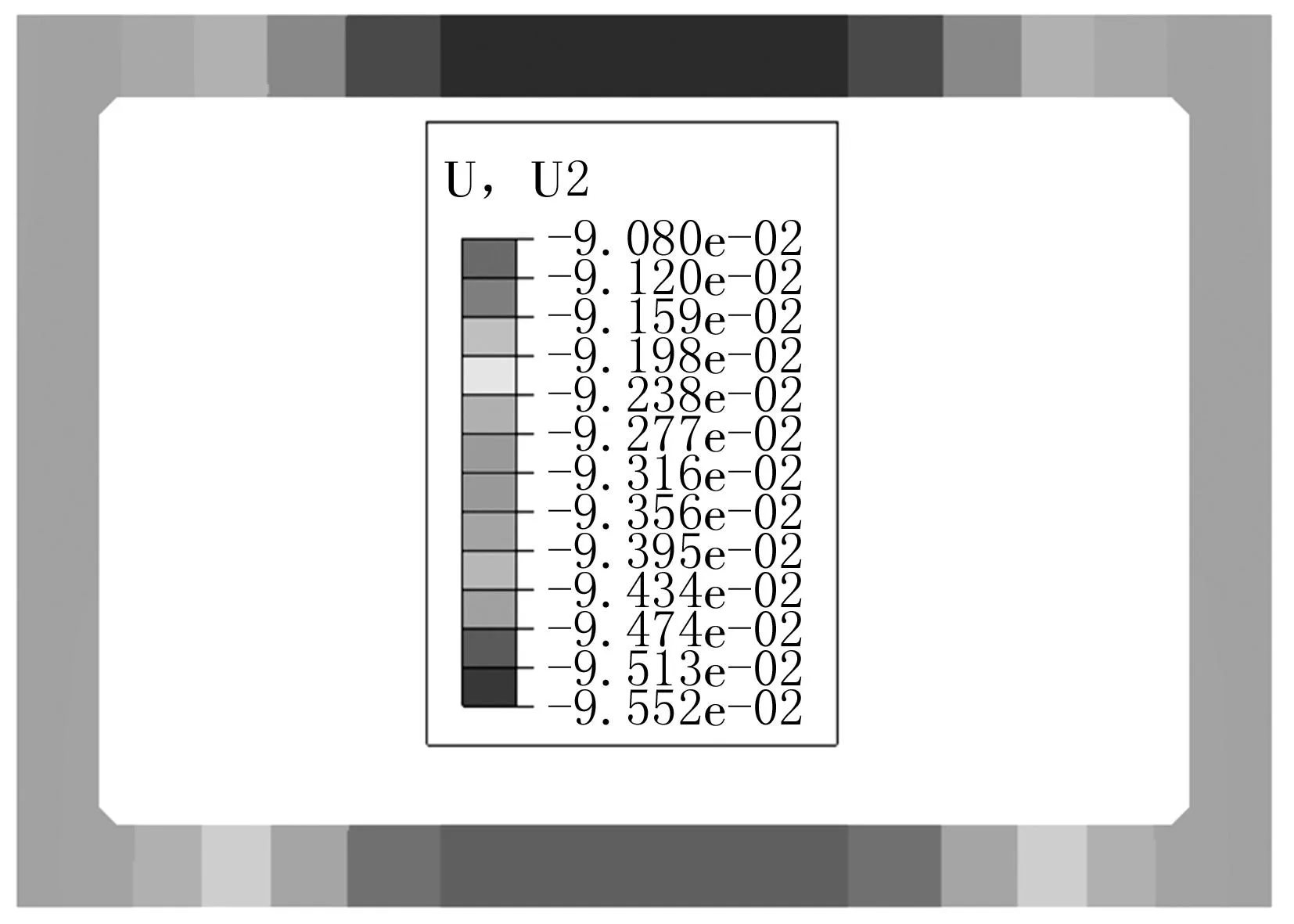
(b)一次分步计算

(c)多次分步计算图6　竖向位移分布云图/m

箱涵结构顶板在图6中(a)、(b)、(c)3种情况下所发生的竖向位移最大值依次为：-8.59 cm、-9.55 cm和-9.53 cm，整体计算结果最小，一次分步计算结果最大，而多次分步计算结果比整体计算结果最大值大10.9%，比一次分步计算结果最大值小0.2%。

箱涵结构底板在图6中(a)、(b)、(c)3种情况下所发生的竖向位移最小值依次为：-8.16 cm、-9.08 cm和-9.06 cm，整体计算结果最小，一次分步计算结果最大，而多次分步计算结果比整体计算结果最小值大11%，比一次分步计算结果最大值小0.22%。

从位移云图的分布上看，3种情况的最大、最小位移区域发生部位基本相同，最大值都位于顶板中部，最小值都位于底板中部。

3设计注意事项及措施

1)对于箱涵应力计算成果中的开裂区域，在设计的过程中应该布置受拉钢筋来减小裂缝的大小或者阻止裂缝的发生，注意受拉钢筋应该采用直径小、间距小的布置方式。

2)从箱涵竖向位移计算成果中可以看出，箱涵发生竖向位移即意味着箱涵发生了沉降，当然了，此沉降包括了箱涵自身的沉降和地基的沉降2个部分。为了减小箱涵自身发生的沉降，在设计过程中可以考虑增大顶底板截面的厚度(即刚度)；为了减小地基的沉降，在设计过程中可以对箱涵的地基进行加固处理。

4结语

1)从应力和位移上看，多次分步计算结果均大于整体计算结果的10%左右，即箱涵的最不利工况出现在施工期，从而说明在进行箱涵的结构计算时，模拟施工填筑过程具有一定的必要性。

2)通过对一次和多次分步计算结果对比分析可以看出，模拟分层填筑过程时也需要合理地划分分层的厚度，才能提高计算结果的准确性。

3)本文虽然对箱涵的施工过程进行了模拟，也与完建期工况(整体计算)进行了对比分析，但是在计算过程中忽略了很多影响因素，例如：网格大小、混凝土的塑性及回填土的压实固结等，因此并未全面准确地体现箱涵的内力及变形，在以后的研究中仍需进一步深入。

4)为了减小箱涵的裂缝和沉降，在设计过程中可以采取一定的措施。

5)考虑到施工分层填筑过程模拟计算的复杂性，仅建议在复杂和重要的工程中进行运用。

参考文献

[1] 李俊伟，李永刚，黄宏伟，等.涵洞施工全过程弹塑性有限元模拟分析[J].岩石力学与工程学报，2005，24(增2):5634-5640.

[2] 韩伟平，马洪亮.涵洞土压力有限元施工分层填筑模拟及试验研究[J].山西水利，2007(4):89-91.

[3] 罗炜华，刘樟富，何晓锋，等.基于施工过程的沟埋式刚性矩形涵洞位移场试验研究与有限元分析[J].中国西部科技，2010，9(4):1-5.

[4] 庄茁.ABAQUS/Standard有限元软件入门指南[M].北京：清华大学出版社，1998.

[5] 陈卫忠，伍国军，贾善坡.ABAQUS在隧道及地下工程中的应用[M].北京：中国水利水电出版社，2010.

doi:10.3969/j.issn.1009-8984.2015.02.004

收稿日期：2015-04-13

作者简介：王志鹏(1984-),男(汉)，河南新乡，工程师，硕士

中图分类号：U449.82

文献标志码：A

文章编号：1009-8984(2015)02-0011-05

The three-dimensional finite element simulation to box-culvert layered filling construction process

WANG Zhi-peng，et al.

(ShenzhenBranchofCSCECAECOMCONSULTANTSCO.，LTD，ShenzhenGuangdong518048，China)

Abstract：A box-culvert three-dimensional numerical model is first established on the basis of ABAQUS finite element in this paper.Then the simulation to box-culvert layered filling construction process by using the multi-step analysis and the birth-death element approach.The layered calculation and overall calculation have been compared in the paper.The comparing results show that both the stress and displacement of box-culvert are higher than about 10% to the overall calculation on the basis of only thinking the elastic properties of concrete and appropriate layered filling construction process.The simulation to box-culvert layered filling construction process can only be established on the complex and important engineering due to the complexity of calculation method and the applicability of the engineering application.

Key words：box-culvert；ABAQUS；layered filling construction；numerical simulation