基于数值模拟的含裂纹BD试验和SCB试验的K因子公式

巫绪涛(1971-)男，安徽合肥人，博士，合肥工业大学副教授，硕士生导师.

基于数值模拟的含裂纹BD试验和SCB试验的K因子公式

胡凤辉,巫绪涛,顾颖,叶波

(合肥工业大学 土木与水利工程学院,安徽 合肥230009)

摘要:文章采用ANSYS程序对含中心裂纹的巴西圆盘(BD)试验和含单边裂纹的半圆弯曲(SCB)试验进行了数值模拟；通过量纲分析,得到了纯Ⅰ型加载条件下BD试验和SCB试验的应力强度因子(K因子)的拟合公式。该公式具有精度较高、形式简单、适用范围宽的优点。对于BD试验,当a/R在0.01~0.8范围内,拟合公式值与有限元模拟值的误差在3.5%以内;对于SCB试验,当s/R在0.4~1.0、a/R在0.01~0.8范围内，拟合公式值与有限元模拟值误差在3.5%以内。

关键词:BD试验;SCB试验;K因子;I型裂纹;数值模拟

收稿日期：2013-12-06；修回日期：2014-01-18

作者简介：胡凤辉(1986-)男，安徽六安人，合肥工业大学硕士生；

doi:10.3969/j.issn.1003-5060.2015.01.020

中图分类号:O343.2文献标识码：A

Kfactorformulabasedonnumericalsimulationof

BDtestandSCBtestwithcrack

HUFeng-hui,WUXu-tao,GUYing,YEBo

(SchoolofCivilandHydraulicEngineering,HefeiUniversityofTechnology,Hefei230009,China)

Abstract:Numerical simulation of Brazilian disk(BD) test with center crack and semi-circular bend(SCB) test with side crack was carried out by using ANSYS program. Through dimensional analysis, the calculation formulas of the K factor of BD test and SCB test under the Ⅰ-type load were gained. The formulas had the advantages of high precision, simple form and wide range of application. For the BD specimen, when the a/R was in the 0.01 to 0.8 range, the formula had high precision and the error was within 3.5% compared with the finite element simulation value. For the SCB specimen, when the s/R was from 0.4 to 1.0, and a/R was in the 0.01 to 0.8 range, the formula had high precision and the error was within 3.5% compared with the finite element simulation value.

Keywords:Braziliandisk(BD)test;semi-circularbend(SCB)test;Kfactor; Ⅰ-typecrack;numericalsimulation

在断裂力学中，脆性材料的断裂韧度研究具有重要的工程应用价值。采用中心裂纹BD试样和单边直裂纹SCB试样，可以方便地实现纯Ⅰ型及Ⅰ、Ⅱ型复合裂纹的加载条件[1]。为了获得试验材料的断裂韧度，必须得到具有较高精度的裂尖K因子计算公式。对于中心裂纹BD试样，文献[2]得到了在裂纹相对长度(裂纹半长a与试样半径R比值)为某些定值时K因子的解析解；在此基础上，文献[1]结合权函数法[3]推导出具有更高精度的K因子公式；但这些公式项数均随裂纹长度增加而显著增多，例如裂纹相对长度0.8时，文献[1]的K因子公式项数多达30项，不方便试验应用。对于单边裂纹SCB试样，由于其复杂的边界条件，很难得到K因子的解析解。文献[4-5]采用有限元法研究了Ⅰ型和Ⅱ型K因子的形函数，但仅限于特定的裂纹相对长度和特定的支座相对间距(支座间距s与试样半径R的比值)，不具备一般性。本文通过数值方法，对纯Ⅰ型加载条件下的2种类型试样的K因子公式进行了研究，当裂纹相对长度和支座相对间距在较宽范围内变化时，2个公式均具有较高的精度，且形式简单，方便于工程应用。

2种试样进行纯Ⅰ型断裂韧性试验的加载示意图如图1所示。

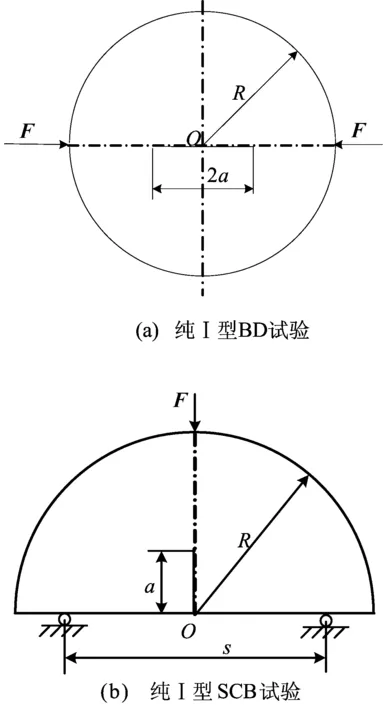
图1　纯Ⅰ型2种试样的断裂韧性试验

1有限元模型以及公式拟合

1.1　有限元模型

按图1所示的BD试验和SCB试验建立有限元模型。2模型均采用线弹性本构；弹性模量E=30GPa,泊松比μ=0.25；单元类型均为SOLID186;为提高模拟精度,围绕裂尖一圈采用退化单元,即单元的1个面退化为裂纹前缘线,与该线垂直的边中节点移至距离裂尖1/4单元边长处[6-8]；裂尖K因子采用相互积分法求解[9]。

2种模型的试样厚度B为0.01m,半径R为0.05m,裂纹相对长度a/R从0.01变化到0.8,承受集中荷载F为9 000 N。另外SCB试样的支座相对间距s/R从0.4变化到1.0。

1.2　BD试验的 K因子公式

根据量纲分析,BD试验的K因子形式如下:

(1)

其中,|F|/(BR)为无裂纹BD试样的中心拉应力量纲,因此(1)式的前半部分具有K因子量纲。当裂纹半长a趋于0时,(1)式趋向于有限宽板解,则f(a/R)为无量纲形状因子,采用(2)式：

(2)

根据有限元得到的K因子离散值拟合(2)式中的系数得到:c1=0.65,c2=-0.66,c3=1.81；拟合效果如图2所示,相关系数为0.999 1,最大误差小于3.5%。

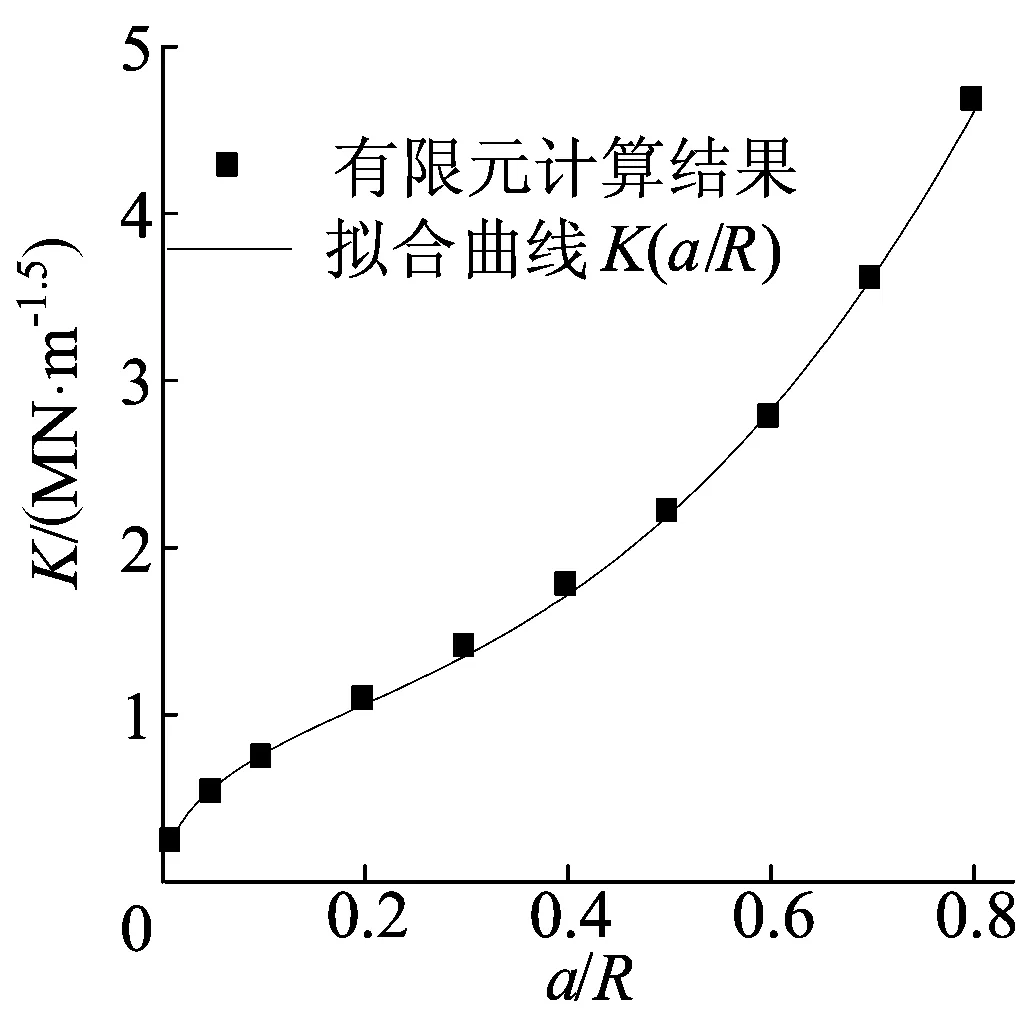
图2　 BD试验K因子拟合曲线

1.3　SCB试验的 K因子公式

采用与BD试验类似的分析方法,SCB试验的K因子具有如下形式

(3)

其中,(3)式的前半部满足K因子的量纲形式;f为无量纲因子。由于SCB试验中支座间距改变导致中心拉应力改变,因此支座相对间距s/R为应力比例因子,裂纹相对长度a/R为形状因子。

为了研究K与s/R的关系,在a/R从0.01变化至0.8、s/R从0.4变化至1.0的范围内进行了大量有限元计算,部分结果如图3所示。

由图3可知,当a/R为定值时，K与s/R具有良好的线性关系,但并不平行,因此(3)式可以进一步转化为:

(4)

令

(5)

则a1、a2分别为图3所示K与s/R系列直线的斜率和截距。根据a1、a2随a/R的变化规律,采用如下多项式：

(6)

(7)

拟合(6)式和(7)式系数可得:d1=4.42,d2=4.10,d3=72.68；e1=-6.99,e2=14.49,e3=-9.58。

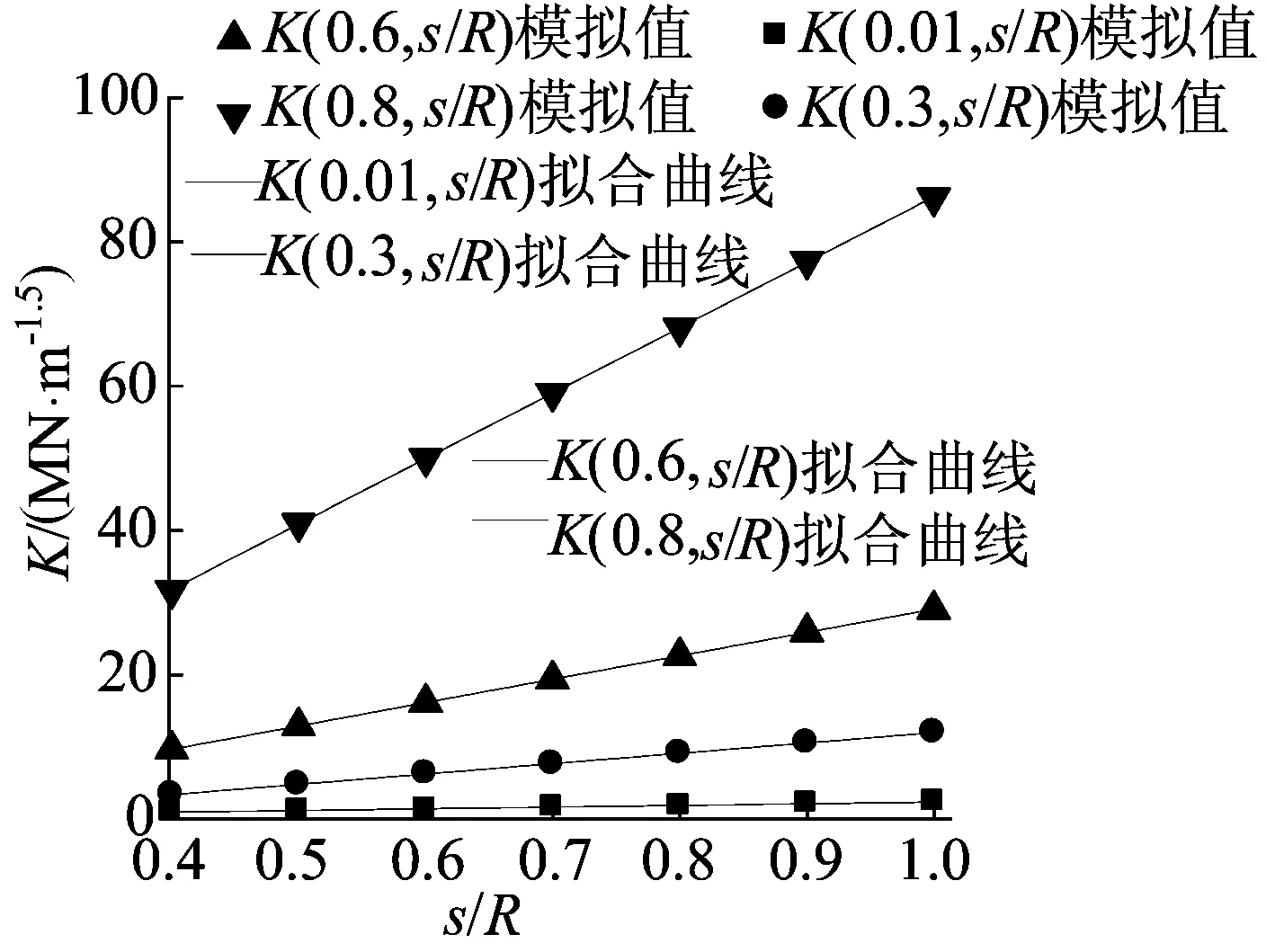
图3　应力强度因子随支座间距的变化关系

a1、a2随a/R变化的拟合效果如图4所示,相关系数分别为0.999 6和0.999 1,最大误差均在3.5%之内。

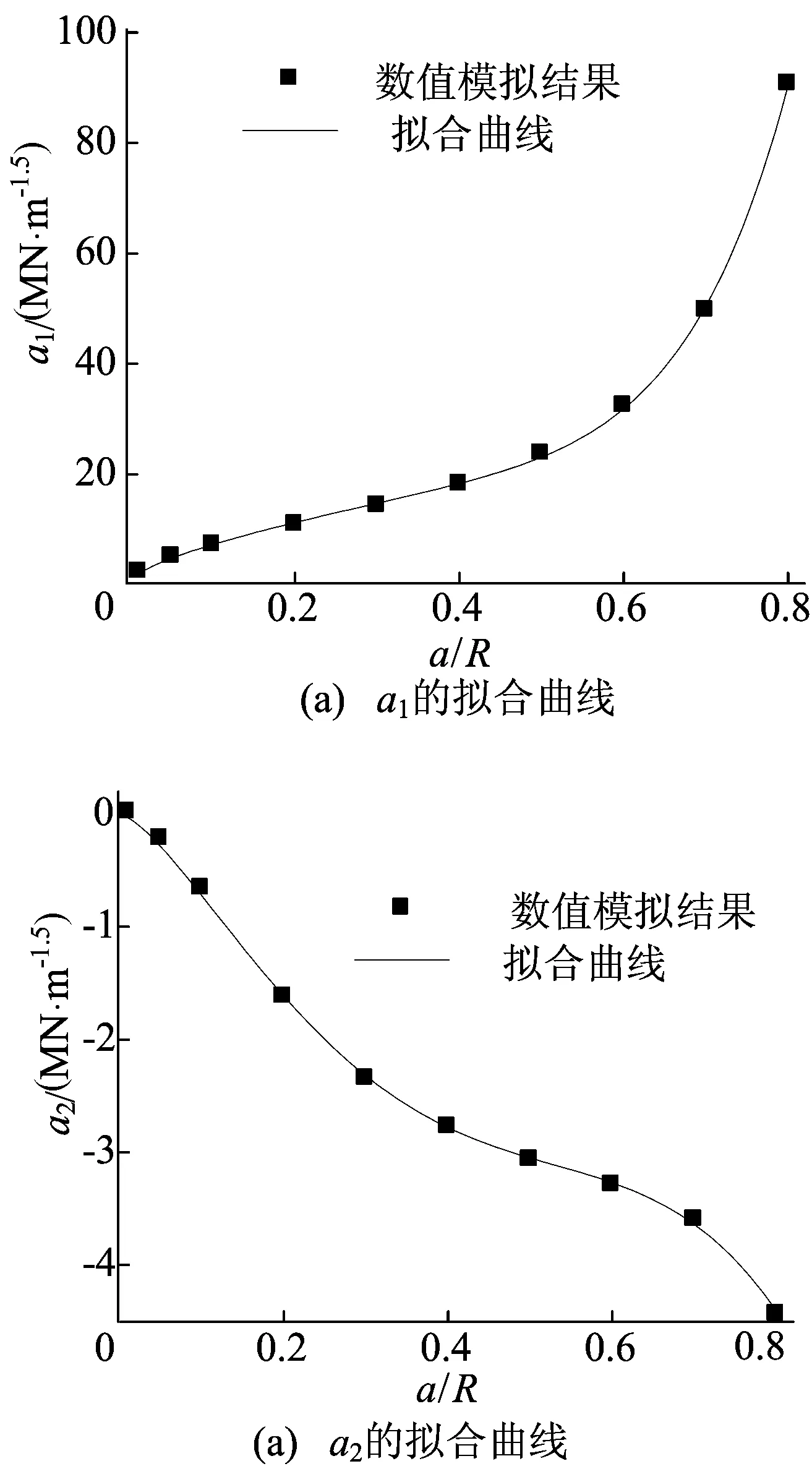
图4　a 1、 a 2随 a/ R变化的拟合曲线

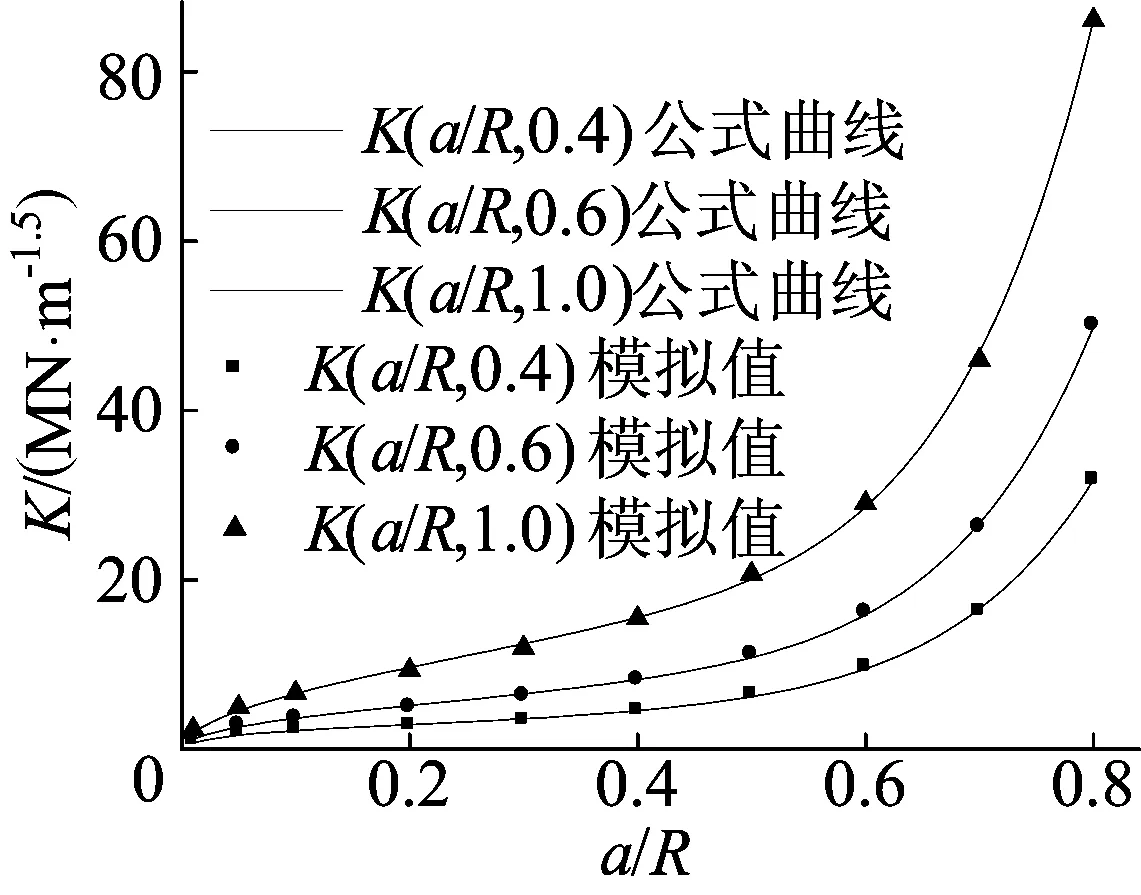
图5　K(a/R,s/R)拟合效果

2结论

本文公式具有较高的精度，计算的K因子值与有限元模拟值的最大误差小于5%。公式适用范围宽。从a/R为0.01的超短裂纹至0.8的长裂纹,SCB试验下支座相对间距s/R从0.4变化至1.0,均完全适用。试验试样的制作不必局限于特定的尺寸,从而解决了传统研究方法中制作误差的影响,便于比较不同长度裂纹对试验结果的影响。相对于解析公式,本文公式非常简洁,更适用于工程应用。

[参考文献]

[1]董世明,汪洋,夏源明.中心裂纹圆盘集中荷载作用下的应力强度因子[J].中国科学技术大学学报,2003,33(3):310-317.

[2]AtksinsonC,SmelserRE,SanchezJ.CombinedmodefractureviathecrackedBraziliandisktest[J].InternationalJournalofFracture,1982,18(4):279-291.

[3]FettT.StressintensityfactorsandT-stressforinternallycrackedcirculardisksundervariousboundaryconditions[J].EngineeringFractureMechanics,2001,68(9):1119-1136.

[4]AyatollahiMR,AlihaMRM.Widerangedataforcracktipparametersintwodisc-typespecimensundermixedmodeloading[J].ComputationalMaterialsScience,2007,38(4):660-670.

[5]AytollahiMR,AlihaMRM,SaghafiH.Animprovedsemi-circularbendspecimenforinvestigatingmixedmodebrittlefracture[J].EngineeringFractureMechanics,2011,78(1):110-123.

[6]巫绪涛,杨伯源.数值外插法求解空间裂纹应力强度因子的研究[J].合肥工业大学学报:自然科学版,1999,22(4):26-31.

[7]瞿伟廉,鲁丽君,李明.带三维穿透裂纹结构的有限元实体建模方法[J].武汉理工大学学报,2008,30(1):87-90.

[8]王锋,黄其青,殷之平.三维裂纹应力强度因子的有限元计算分析[J].航空计算技术,2006,33(3):125-127.

[9]张洪才.ANSYS14.0理论解析与工程应用实例[M].北京:机械工业出版社,2012:456-486.

(责任编辑胡亚敏)