基于连分式的广义高斯模型UDCT贝叶斯图像去噪

基于连分式的广义高斯模型UDCT贝叶斯图像去噪

杨兴明,牛坡礼

(合肥工业大学 计算机与信息学院,安徽 合肥230009)

摘要:文章通过研究均匀离散曲波变换(uniform discrete curvelet transform,UDCT)系数统计特性,发现该变换域的系数具有良好的相关性,且能有效解决广义高斯模型的参数拟合问题。在利用广义高斯模型的参数估计进行图像去噪过程中,从矩估计和最大似然估计出发,采用比牛顿迭代法更稳定的连分式迭代法来求解最大似然估计的超越方程;采用蒙特卡洛方法代替鲁棒中值法来精确地估计每个子带的噪声方差;在Bayesian最大后验概率估计的框架下完成图像去噪。实验结果表明,文中提到的算法与传统的VisuShrink、BayesShrink和SureShrink相比,具有较好的去噪效果和峰值信噪比。

关键词:广义高斯模型;连分式迭代法;均匀离散曲波变换;蒙特卡洛方法

收稿日期：2013-11-25；修回日期：2014-03-26

基金项目：安徽省自然科学基金资助项目(090412041)

作者简介：杨兴明(1977-),男,云南安宁人,博士,合肥工业大学副教授,硕士生导师.

doi:10.3969/j.issn.1003-5060.2015.01.011

中图分类号:TP751.1文献标识码：A

Bayesian image denoising by generalized Gaussian

model based on UDCT and continued fraction

YANG Xing-ming,NIU Po-li

(School of Computer and Information, Hefei University of Technology, Hefei 230009, China)

Abstract:Based on the researches on statistical properties of the coefficients of uniform discrete curvelet transform(UDCT), it is discovered that the coefficients of transform domain have good correlation, and can be used to solve the problem of parameter fitting in generalized Gaussian model effectively. Firstly, in view of the moment estimation and maximum likelihood estimation, the continued fraction iteration method is used, which is more stable than Newton iteration method, to make the maximum likelihood estimation of transcendental equation in the process of image denoising by using the generalized Gaussian model parameter estimation. Then the Monte Carlo method is used to estimate each subband noise variance accurately instead of robust median method. Finally, the image denoising is completed in the framework of Bayesian maximum posterior probability estimation. The experimental results show that the proposed algorithm has good denoising effect and peak signal-to-noise ratio(SNR) in comparison with traditional methods such as VisuShrink, BayesShrink and SureShrink.

Key words:generalized Gaussian model; continued fraction iteration method; uniform discrete curvelet transform(UDCT); Monte Carlo method

在多尺度的变换域中,子带系数的建模是图像处理领域的基础,也是该领域的瓶颈。广义高斯分布[1]的提出有效地解决了该问题,并伴随着新型小波变换的出现逐步发展。在ridgelet变换的基础上,文献[2]提出了目前理论最完备的curvelet变换,但其应用性较差。文献[3]提出与实际的工程应用比较接近的contourlet变换,该变换将图像的多尺度和多方向表示灵活而有机地结合起来,其变换域中多重子带的边缘分布也能充分反映其特征,但缺乏理论基础。文献[4]结合curvelet变换的理论完备性和contourlet变换工程的应用性,提出了均匀离散曲波变换(uniform discrete curvelet transform,UDCT),为广义高斯分布的建模构建了良好的平台。经研究表明,均匀离散曲波变换域系数呈尖峰、长拖尾的性质，非常适合广义高斯分布来拟合,因此在UDCT变换域进行广义高斯分布统计建模及应用有着重要的意义[5-6]。

1广义高斯模型建模和参数估计

大量的研究表明,变换域内图像的小波系数在尺度间和尺度内均存在一定的相关性,而正确地利用这些相关性可以显著地改善有关算法的性能,本文依据尺度内小波系数的相关性,提出了广义高斯分布,它不仅涵盖了拉普拉斯分布、高斯分布及均匀分布,而且其尖峰长拖尾的性质很适合广义高斯模型来拟合。本文在小波系数分布基础上,建立广义高斯模型。

1.1　广义高斯模型的建立

定义1广义高斯模型的一般形式如下:

(1)

其中,α、β分别为该模型的尺度参数和形状参数;

σx为该模型的标准差。

各变换域内小波系数的分布与广义高斯模型的拟合程度如图1所示。

图1　小波系数统计直方图

1.2　广义高斯模型的参数估计方法

建立广义高斯模型后,通过计算估计得到该模型中的参数α、β、σx是图像去噪的关键环节,传统的广义高斯分布包括矩估计、熵匹配估计[7]和最大似然估计。研究表明,矩估计更适合形状参数较大时;当形状参数较小、样本较小时，适合采用熵匹配估计;当形状参数较小、样本较大时，适合采用最大似然估计。对于图像而言,样本集合比较大,较适合应用最大似然估计。

1.2.1　矩估计

对于广义高斯分布,有α和β2个未知参数,则需要计算样本的1阶和2阶样本矩来计算样本的期望和方差。假设变换域的小波系数样本集X={x1,…,xN},则可得1阶矩和2阶矩。

1阶矩：

(2)

2阶矩：

(3)

由广义高斯模型的定义和矩估计算式可得:

(4)

令A1=a1,A2=a2,可得:

(5)

1.2.2　最大似然估计

假设集合X={x1,…,xN}是独立分布的,则其似然函数为:

(6)

对(6)式求α和β偏导数可得:

(7)

(8)

由(7)式可得:

(9)

(10)

该方程没有解析解,只能通过迭代的方法得到,传统的迭代法包括牛顿迭代法、最速下降法等,但这几种迭代运算太复杂,为克服计算量大的不足,本文引入一种连分式迭代法[8]。

1.2.3　连分式迭代法的实现

本文引入反差商概念。现给定数据中DN={(βi,yi)|i=0，1，2,…,N,βi互异}，而yi=y(βi)。

定义2

(11)

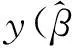
定理1设

其中,φ(β0,β1,…,βn)≠0,k=0,…,n为y(β)在β0,…,βk处的k阶反差商,则有Rn(βi)=y(βi),i=0,1,…,n。

证明假设R(β)=P(β)/Q(β),而

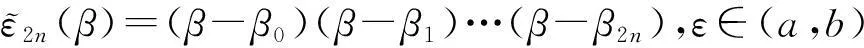
(12)

令β=βi,则有:

通过递归的方法可得:

(13)

将β0,…,βk带入(13)式可得：Rn(βi)=y(βi),i=0,1,…,n。

定理得证。

(13)式是连分式的基本形式,特别地,当n=2时，构造的连分式如下:

其中,β0、β1、β2通过矩估计得到。

令R(β)=0,可得:

由此构造的迭代式如下:

(14)

令dk+1=φ(βk,βk+1),dk+2=φ(βk,βk+1,βk+2),dk=βk。本文通过连分式迭代法得到允许的误差范围ξ下的最终解β。连分式的实现步骤如下:

(1) 由矩估计得到β0、β1、β23个初始值,并计算得到y0、y1、y2。

(2) 利用(11)式可得φ(βk,βk+1)、φ(βk,βk+1,βk+2),得到dk、dk+1、dk+2，其中，k=0,1,2,…。

(3) 由(14)式得到βk+3,即新的dk。

(4) 选取ξ=0.000 001作为允许误差范围,若|βk+3-βk+2|<ξ,停止迭代,βk+3即为所求解;否则由(10)式计算yk+3,并依此更新βk=βk+1、βk+1=βk+2、βk+2=βk+3和yk=yk+1、yk+1=yk+2、yk+2=yk+3。

2蒙特卡洛法参数估计

传统的阈值去噪中,均用鲁棒中值法估计各个子带的噪声方差,本文采用蒙特卡洛方法,该方法能逼真地描述具有随机性质事物的特点及物理实验过程,结合噪声中的高斯白噪声,其特性非常吻合。由于均匀离散曲波变换域的各个尺度、各个子带的方差近似相同,采用该方法可以得到各个尺度、各个子带内对应于每个图像系数的噪声系数方差,具体实现步骤如下:

(1) 对含噪的图像进行正交变换,鲁棒中值法估计出噪声标准差σn,即

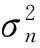
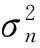
3基于广义高斯模型的贝叶斯图像去噪

在经典的Bayesian的最大后验估计理论的框架下,得到适合于UDCT的基于Bayesian准则的图像去噪方法,现描述如下。

x=y+w

(15)

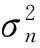
(16)

为了求出y,由最大后验概率估计可得:

(17)

在模拟噪声方差的计算中,本文采用蒙特卡洛方法可得:

(18)

对(18)式取对数可得:

(19)

为了得到使后验概率密度函数最大时的y,对(19)式进行x求导可得:

(20)

特别地,当β=1时,

(21)

当β=2时,

(22)

在形状参数β越大时,误差越大；β越小，越适合最大似然估计,可得图像去噪算法的步骤为:

(1) 对含噪图像进行UDCT得到相应变换域的小波系数。

(3) 通过建模可得含噪图像的参数α和β，并得到含噪图像的方差σ2,将结果带入(21)式,得到去噪后的小波系数。

(4) 对处理后的小波进行UDCT逆变换得到相应的图像。

4实验结果与分析

本实验采用512×512的Lena图像,取噪声方差σn为35,并与经典的VisuShrink[8]、BayesShrink[9]、SureShrink[10]方法进行比较,结果如图2所示。

图2　各种去噪方法所得去噪后的图像

本文采用均方误差(MSE)和峰值信噪比(PSNR)作为评价图像去噪的标准，不同方法去噪的均方误差(MSE)和峰值信噪比(PSNR)的效果对比见表1所列。

表1　不同去噪方法的 PSNR和 MSE统计对比　 dB

实验中取噪声标准差σn分别为15、25、35。由表1可以看出，MSE和PSNR2项指标都有明显改善，同时算法的改善也带来算法的复杂度,因此实验时间也有所增加。

5结束语

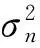
[参考文献]

[1]MallatSG.Atheoryformultiresolutionsignaldecomposition:thewaveletrepresentation[J].IEEETransactionsonPatternAnalysisandMachineIntelligence,1989, 11(7):674-693.

[2]CandèsEJ,DonohoDJ.Curvelets：asurprisinglyeffectivenonadaptiverepresentationforobjectswithedges[R].VanderbiltUniversity,2000.

[3]DoMN,VetterliM.Thecontourlettransform:anefficientdirectionalmultiresolutionimagerepresentation[J].IEEETransactionsonImageProcessing,2005,14(12):2091-2106.

[4]NguyenTT,ChaurisH.Uniformdiscretecurvelettransform[J].IEEETransactionsonSignalProcessing,2010,58(7):3618-3634.

[5]吴保奎，范素凤.改进的基于小波变换SAR图像去噪方法的性能评价[J].合肥工业大学学报：自然科学版，2006，29(3)：379-381.

[6]AiazziB,AlparoneL,BarontiS.EstimationbasedonentropymatchingforgeneralizedGaussianPDFmodeling[J].IEEESignalProcesssingLetters,1999,6(6):138-140.

[7]王仁宏,朱功勤.有理函数逼近及其应用[M].北京:科学出版社,2004:32-35.

[8]DonohoDL,JohnstoneIM.Idealspatialadaptationbywaveletshrinkage[J].Biometrika, 1994,81(3):425-455.

[9]ChangSG,YuB,VetterliM.Adaptivewaveletthresholdingforimagedenoisingandcompression[J].IEEETransactionsonImageProcessing,2000,9(9):1532-1546.

[10]DonohoDL.De-noisingbysoft-thresholding[J].IEEETransactionsonInformationTheory, 1995,41(3):613-627.

(责任编辑闫杏丽)