A Finite Element Procedure for Analysis of Chemo-Mechanical Coupling Behavior of Hydrogels

Wei Wei,Qingsheng Yang

A Finite Element Procedure for Analysis of Chemo-Mechanical Coupling Behavior of Hydrogels

Wei Wei1,2,Qingsheng Yang1,3

Chemo-mechanical coupling behavior of materials is a transformation process between mechanical and chemical energy.In this paper,based on the coupled chemo-mechanical constitutive equations and governing equations during isothermal process,the equivalent integral forms of chemo-mechanical coupling governing equations and corresponding finite element procedure are obtained by using Hamilton’s principle.An isoparametric plane element for chemo-mechanical coupling is associated into ABAQUS finite element package through user element subroutine UEL.The numerical examples exhibit that the ionic concentration variation can cause mechanical deformation and mechanical action can produce redistribution ofionic concentration for hydrogels.It is proved that the present developed chemo-mechanical coupling finite element procedure can be utilized to model the coupling behavior of hydrogels effectively.

Hydrogel;Chemo-mechanical coupling;Hamilton’s principle;Coupled finite element method.

1 Introduction

The hydrogel is a kind ofintelligent soft polymer materials generally composed of crosslinked polymer network,solvent and ions,with physical properties of swelling with water absorption,and dehydration shrinkage.Under the external field(such as heat,electricity,magnetism,chemistry,light,etc),the hydrogel can exchange energy and substance and produce a large mechanical response exhibiting obvious multi-field coupling characteristics, and that is the thermo-electro-chemo-mechanical coupling behavior.

According to the responses under different external environmental stimulus,hydro-gels can be divided into temperature-sensitive,pH-sensitive,electrical-sensitive,bio-response and pressure-sensitive types,etc[Ullah,Othman,Javed,Ahmad,and Akil(2015)].Over the past decades,it has rapid development in fundamental and applied research for hydrogels.Due to such characteristic behaviors,many hydrogel-based networks have been designed and fabricated to meet the needs ofindustrial and medical fields etc.At present,the hydrogels have been used in wide fields,such as tissue engineering[Thankam and Muthu(2015);Nawrotek,Tylman,Rudnicka,Balcerzak,and Kaminski(2016)],biological and food Engineering[Gregorova,Saha,Kitano,and Saha(2015);Wu,Degner,and McClements(2014)],actuators and sensors[Rivero,Molina,Rivarola,and Barbero(2014);Ionov(2014)],drug delivery[Li,Fan,Ma,Zhu,Luo,Liu,and Chen(2014);Sagiri,Singh,Kulanthaivel,Banerjee,Basak,Bat-tachrya,and Pal(2015)],contact lenses[Maulvi,Soni,and Shah(2015);Filipecki,Sitarz,Kocela,Kotynia,Jelen,Filipecka,and Gaweda(2014)],packers in oilfields[Gu,Liu,Chai,Li,and Sun(2014);Tongwa and Bai(2014)],and wound dressings[Zheng,Xue,Wei,Li,Xiao,and Guan(2014);Gonzalez,Ludueña,Ponce,and Alvarez(2014)].

Due to the wide applications of hydrogels,it is an important practical significance to study their physical properties and multi-field coupling characteristics.The phenomenological continuum mechanics is an effective way to study the coupled problem.Grimshaw,Nussbaum,Grodzinsky,and Yarmush(1990)proposed an electrochemical coupling equation to describe the swelling of a polymer dielectric gel.De,Aluru,and Johnson(2002),De and Aluru(2004)employed electrochemo-mechanical model to develop equilibrium expansion and dynamic behavior of the pH-responsive hydrogel.Kang,Dai,Shen,and Chen(2008)established electro-chemo-mechanical coupling model and studied the dynamic behavior of the swelling or shrinkage for the pH-sensitive gel.Wallmersperger and co-workers presented a coupled electro-chemo-mechanical equation and finite element method for polyelectrolyte gels,and applied a fully coupled electro-chemo-mechanical model to analyze the effect of electrical and chemical stimulation on hydrogels,respectively[Wallmersperger,Kröplin,and Gülch(2004);Wallmersperger and Ballhause(2008);Ballhause and Wallmersperger(2008)].Li and co-workers developed an electro-chemo-mechanical model with Poisson-Nernst-Planck(PNP)equations,and studied the influences of the ionic strength in surrounding solution on the distribution of the diffusive ions concentration and electric potential as well as the deformation for the pH-stimulus-responsive hydrogel[Li,Ng,Yew,and Lam(2005);Li,Ng,Yew,and Lam(2007);Li and Yew(2009)].Additionally,Li(2009)published a monograph on the fundamental theory modeling and numerical simulation of the smart hydrogels,and systematically documented the response behaviour of the smart hydrogels to various environmental stimuli.Yang and co-workers introduced the chemical effect into the free energy,to build thermo-electro-chemo-mechanical coupled constitutive equations for hydrogels.The coupled finite element program was presented to analyze chemo-mechanical coupling problems[Yang,Liu,and Meng(2009);Yang,Qin,Ma,Lu,and Cui(2010)].Yang,Ma,and Shang(2013)analyzed chemo-mechanical coupling behavior of hydrogel composite beams by using the general form of free energy density function for a neutral hydrogel.

In recent years,many studies aimed to develop a finite element method for large deformation of hydrogels based on a nonlinear continuum theory.Hong,Zhao,Zhou,and Suo(2008);Hong,Liu,and Suo(2009)formulated a theory of the coupled mass transport and large deformation with the free-energy function and implemented this approach in ABAQUS to analyze examples of swelling-induced deformation,contact,and bifurcation in polymeric gels.Duda,Souza,and Fried(2010)presented a theory about a mechanical deformation and a migration of a chemical species by employing the principle of virtual power,to study the polymer network swelling with the influences of mechanical and chemical interactions.Marcombe,Cai,Hong,Zhao,Lapusta,and Suo(2010)developed a theory of constrained swelling for the pH-sensitive hydrogel and a network of polymers in equilibrium with an aqueous solution and mechanical forces.Zalachas,Cai,Suo,and Lapusta(2013)investigated the large and inhomogeneous deformation and creasing instability by using the developed nonlinear field theory and finite element method for pH-sensitive hydrogels.Lucantonio,Nardinocchi,and Teresi(2013)used the finite element software package COMSOL to perform several numerical simulations for transient swelling-induced large deformations in polymeric gels.Ding,Liu,Hu,Swaddiwudhipong,and Yang(2013)studied inhomogeneous deformation in the temperature-sensitive hydrogel with many meaningful numerical results using a user-supply subroutine in ABAQUS.Duan,Zhang,An,and Jiang(2013)and Toh,Liu,Ng and Hong(2013)used the built-in thermo-mechanically coupled finite elements to simulate the transient diffusion and swelling kinetics of polymeric gels by adopting an analogy between diffusion and heat transfer in solids in ABAQUS.Chester,Di Leo,and Anand(2015)summarized the theory in Chester and Anand(2011)for fluid diffusion and large deformations of non-ionic elastomeric gels.Several illustrative numerical simulations are applied to demonstrate the correctness of the numerical implementation described in detail with ABAQUS software.Bouklas,Landis,and Huang(2015)implemented a mixed finite element method in ABAQUS by introducing a finite bulk modulus in the nonlinear continuum theory proposed by Hong,Zhao,Zhou,and Suo(2008),with specific attention to the numerical stability issues associated with the Ladyzhenskaya–Babuska–Brezzi(LBB)condition for spatial discretization.

In this paper,starting from the laws of thermodynamics,by establishing a phe-nomenological free energy density function and introducing the definition of chemical potential in classical physical chemistry,continuum mechanics approach is developed to derive chemo-mechanical coupled constitutive equations and governing equations during isothermal process.By employing Hamilton’s principle,the equivalent integral forms of chemo-mechanical governing equations and corresponding finite element equations are derived.To implement the finite element calculation,a user element subroutine UEL in ABAQUS package is developed and an isoparametric plane element for chemo-mechanical coupling behavior is programmed.Physical properties of hydrogels in chemo-mechanical coupling field are analyzed by means of typical numerical examples.

2 Basic equations

2.1 Governing equations of the chemo-mechanical coupling problem

In this section,based on the laws of thermodynamics,the chemo-mechanical coupled constitutive equations and governing equations during isothermal process are summarized.

It is assumed that the medium(volumeV,boundary Γ)is subjected to the chemical and mechanical stimuli simultaneously,and therefore there exists a mutual coupling effect between two fields.For example,the changes ofion concentration can induce the osmotic pressure during the mixed diffusion process with ions and mediums.The chemo-mechanical coupling problem needs to satisfy the general mass,momentum and energy conservation equations,and every physical field should comply with their governing equations and boundary conditions.

The governing equation of mechanical field is

The natural(stress)boundary condition and forced(displacement)boundary condition are

The gradient equation of mechanical field is

where σijis stress;εijis strain;fiis unit volume force;uiis displacement;¯tiis the applied surface force on the boundary;¯uiis specified displacement on the boundary;Γtis specified force boundary;and Γuis specified displacement boundary.

In classical physical chemistry[Levine(2002)],the chemical potential is expressedwhereµ0is the chemical potential in the reference state;R∗is the universal gas constant;Tis the reference temperature;c0is the ion concentration;andcis the increment of the ionic concentration.A partial derivative with respect to concentration yields∂µ/∂c=R∗T/(c0+c).For a small increment of the concentration,we havec0+c≈c0.Thus,the Fick’s second law describing the non-steady diffusion process can be represented by

where ξiis the diffusion flux ofions,and τ0=R∗T/c0.The natural(chemical flux)boundary condition and forced(ion concentration)boundary conditions for chemical field are

where Γξand Γcare the boundaries subjected to the ion fl ux and concentration,respectively;ξnis the given ion fl ux on the boundary Γξ;andc¯ is the given concentration increment on the boundary Γc.The gradient equation for chemical diffusion is given by

where ϕijis the chemical diffusion coefficient ofions in medium.

According to the law of thermodynamics,and omitting the electrostatic effect in the electrostatic field of the constituents,the differential form of the total internal energy density composed of the elastic energy,the chemical energy and thermal energy is formulated as Yang,Liu,and Meng(2009)

whereTis temperature;Sis entropy;and α denotes the number ofion species.The classic form of Helmholtz free energy is defined by

According to Eqs.(7)and(8),the differential form of Helmholtz free energy in the system in chemo-mechanical coupling field can be expressed as

where three terms on the right side represent the incremental form of energy contribution in mechanical field,chemical field and temperature field,respectively.

Considering an isothermal process,namely the temperature increment dT=0,the canonical equations in chemo-mechanical coupling can be obtained as follows

Taking the small strain and the small concentration increment as the independent variables,respectively,the Helmholtz free energy during the isothermal process can be expanded by using Taylor’s series

where ε0,c0are the strain and the concentration in the initial state,respectively.It is assumed that the material parameters can be defined as

wherecijklis the stiffness coefficient under constant concentration;sis the chemical potential coefficient ofions under constant strain;andis the chemo-mechanical coupling coef ficient.

According to Eqs.(10)–(12),and omitting the quadratic terms,a linear constitutive relation At the equilibrium state in coupled chemo-mechanical field can be given as

It is noted that in classic physical chemistry,chemical potential and ionic concentration have logarithmic relations.However,the present linear constitutive equation is still reasonable when the concentration transformation is even small.The coupling coefficients in constitutive equations can be achieved through theoretical derivation and regular mechanical experiments[Qin and Yang(2008)].

For the medium bathed in a solution,only one ofions plays a dominant role,Eqs.(13)and(14)can be simplified as

Eqs.(15)and(16)are fully coupled equations in chemical and mechanical field,respectively.The hydrogel is essentially a porous media containing interstitial fluid.The deformation in porous media is controlled by complete stress corresponding to external loading and superposition value in pore-fluid pressure.The effective stress[Terzaghi,Peck,and Mesri(1996)]is

Comparing the constitutive relation Eq.(15)with the effective stress Eq.(17),it is found thatpδij=Rijcis the pressure caused by ionic diffusion.The theory of thermodynamics[Flory and Rehner(1943a,b)]considered that the pressure causing swelling in hydrogels consists of three parts:mixing pressure in polymer and solution,elastic deformation pressure of the chains in polymer network,and osmotic pressurepioncaused by the concentration difference ofions inside and outside the colloid.This paper only considers the osmotic pressure caused by concentration difference ofions inside and outside the hydrogel derived from the Donnan osmotic pressure.The osmotic pressure caused by concentration difference is

By using this equation,we can obtain the chemo-mechanical coupling coefficientRij=R∗Tδij.

A partial derivative with respect to concentration for Eq.(16)leads to chemical potential coefficients=R∗T/(c0+c).If the concentration undergoes a very small increment,it can be approximately considered ass=R∗T/c0.Thus the chemomechanical coupling constitutive equations during isothermal process can be written as

where εmis the volume strain in the system.

2.2 The hamilton’s principle and finite element procedure

The Hamilton’s principle can be used to derive governing equations and natural boundary conditions for the fully chemo-mechanical coupled theory.The power generated by the kinetic energy density[Mindlin(1974)]in the system is

Becauseui(t1)andui(t2)are known,there is δui(t1)= δui(t2)=0.Thus Eq.(22)becomes

whereUis total potential energy in the system.The rate of potential energy can be read

whereVis the volume in region;Γ is the surface in region;ψ is a generalized free energy density in the system,δ˙ψ=σijδ˙εij+˙µδc;andPcis the chemical diffusion power ofions,[Yang,Qin,Ma,Lu,and Cui(2010)].

According to Hamilton’s principle,we have

It is noted that δu˙i,δcare independent variables,and the governing equations and the natural boundary conditions can be obtained in the mechanical and chemical field,respectively.In other words,Eq.(29)is equivalent to the governing Eqs.(1)and(2)and the natural boundary conditions(4)and(5)completely.Eq.(29)is the weighted residual form of the natural boundary conditions and governing equations in two physical fields.This means that the present chemo-mechanical coupling theory is completely closed.

The Eq.(27)can be written for the following form

Therefore,it can be obtained that

To produce the finite element equations,the displacement and concentration increment are interpolated by

whereare the shape functions of displacement and concentration,respectively;andare the nodal displacement and concentration vectors,respectively.

where superscriptTis the vector transpose.Substituting discrete forms of the displacement and concentration increment,we can get

Whereis the elastic constant matrix;is the mechanical strain matrix;is the strain matrix of volume strain;is the strain matrix of concentration gradient;andis the coefficient matrix of chemical diffusion.The independence ofandyields

Thus,the finite element equations of chemo-mechanical coupling can be get

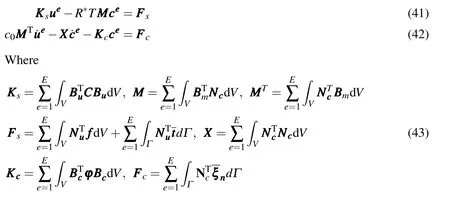
A linear difference method can be performed in the time domain.In∆t=tn+1−tn,the linear interpolations are

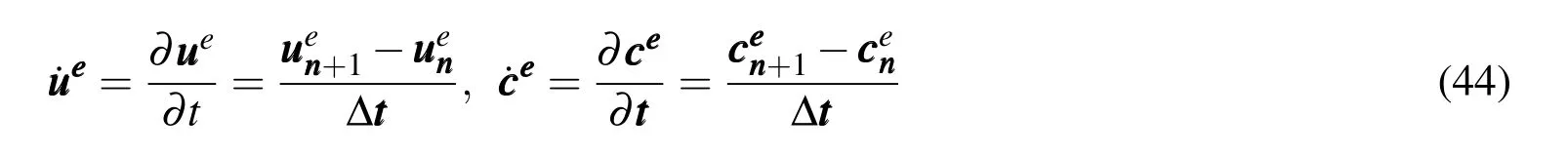
Applying the formulas ofue=θuen+1+(1−θ)uenandce=θcen+1+(1−θ)cenin which θ is the interpolation parameter,substitution of equations above into E-qs.(41)and(42)leads to

When θ=1,the fully implicit method can be used to produce relatively smooth results,and not to result in shock phenomena[Smith and Griffths(2003)].It is concluded that

3 The verification and application of the user element subroutine UEL

The hydrogel is really a porous medium composed of the solid skeleton and porefluid.The structure of the applicable hydrogel is relatively complex,and nonuniform deformation behavior will be produced under the chemo-mechanical coupling.Numerical methods are widely used for solving coupled chemo-mechanical problems for hydrogels owing to great difficulties to obtain analytical solutions.

To implement the finite element equations derived,the user element subroutine UEL is developed by using the software ABAQUS,and an isoparametric plane eight-node element for chemo-mechanical coupling is programmed.Here a few examples can be applied to verify the accuracy of the user element subroutine UEL programmed.

Figure 1:Schematic of the model.

3.1 Example 1

As a first example,there is a 20×50(mm)2hydrogel plane in which BC boundary is constrained and AB boundary is contact with the solution as shown in Fig.1.

The material parameters of the hydrogel are listed in Table 1[Loret,Simoes,and FMF(2005)].The initial concentration of the hydrogel isc0=250 mol/L.Three cases are studied here.Case 1:a uniform forceq=1 × 10−4N/mm is applied on the left side AB;Case 2:a solution concentrationcw=500 mol/L is applied on the right side CD;Case 3:the uniform forceq=1 × 10−4N/mm on the left side AB and the concentrationcw=500 mol/L on the right side CD are applied simultaneously.

Table 1:Material parameters of the hydrogel plane.

As seen from Figs.2 and 3,the concentration at points B and G in Fig.2 and the concentration at points D and M in Fig.3 increases quickly during the initial time in coupling state,respectively,and then the increasing trend of the concentration slows down gradually.After the timet=6000 s,concentration values do not change,which proves that the whole system reaches the force equilibrium state and the diffusion equilibrium state att=6000 s.

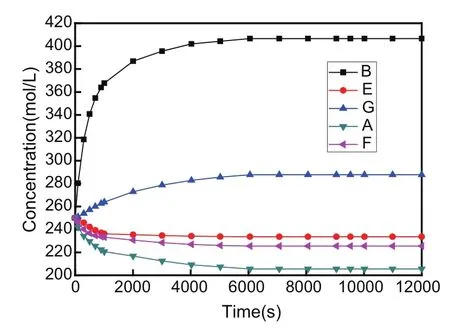
Figure 2:The concentration at AB side in coupling state versus time.

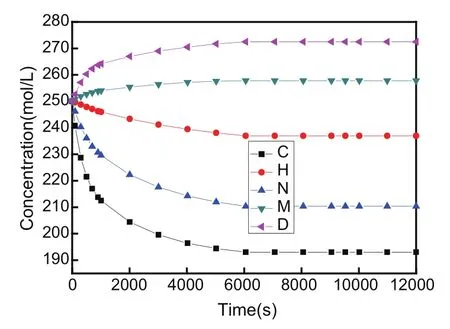
Figure 3:The concentration at CD side in coupling state versus time.

Furthermore,the concentration at points E,F and A in Fig.2 and the concentration at points H,N and C in Fig.3 decreases quickly in coupling state,respectively,and then the decreasing trend of the concentration gradually slows down too.However,the concentration eventually changes to a constant value after the equilibrium state.At the equilibrium state,the maximum and minimum of the concentration on the left side AB lie in point B and point A as shown in Fig.2,respectively.Besides,the maximum and minimum of the concentration on the right side CD locate in point D and point C in Fig.3,respectively.Thus,it is observed that the variation of the concentration is different between the upper and lower parts of plane because of the constraint effect on the bottom side BC.At the equilibrium state,the point of maximum concentration is located in the lower left corner point B,and the point of minimum concentration is located in the lower right corner point C in the whole plate.

Therefore,the variation of the concentration versus time is dissimilar in different sample positions.There exist various points with increasing and decreasing concentration,respectively.The diffusion phenomenon of the external concentration can lead to concentration redistribution inside the whole plane.If somewhere the concentration increases,inevitably the concentration decreases in another position during which the mechanical energy and chemical energy can be transformed into each other.That is to say,a new balance state would be reached gradually with increase of time.

As seen from Figs.4 and 5,the variation of the concentration at each point on AB and CD sides is dissimilar in three cases.Yet,concentration values in coupling state lie between those in two other states,which confirms the chemo-mechanical coupling behavior obviously.Additionally,it is shown that physical effective properties are changed due to the chemo-mechanical coupling in the hydrogel plate,which influences the behaviors of diffusion and deformation simultaneously.

Figure 4:The concentration at AB side in three cases side.

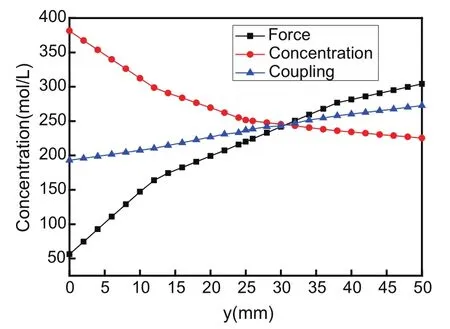
Figure 5:The concentration at CD in three cases.

Fig.6(a)shows the undeformed gridding mesh of the hydrogel plane with constraint conditions at the initial time in Abaqus software.By the way,every subfigure(a)for all figures below in this paper represents the initial undeformed gridding mesh with constraint conditions,respectively.In Fig.6(b)–(d),the invariant black gridding lines in each subfigure indicate the original reference body,which is similar to the following figures in this paper.The hydrogel plane presents coupled deformation when concentration and force are applied simultaneously in Fig.6(c),which coincides with the literature in Wallmersperger,

Wallmersperger,Kröplin,and Gülch(2004).As seen from the example,there exists obvious coupling phenomena in chemical and mechanical field under the combination of force and concentration in hydrogels.Changes of concentration can cause mechanical deformation of the medium,and mechanical stimulations can lead to concentration redistribution too.

3.2 Example 2

Let us consider the second example.As shown in Fig.7,there is a simply supported rectangular hydrogel bar in its middle whose upper side is contact with the solution.The values of material parameters for the list{E,R∗,T,ν}in our simulation for the transient swelling problem are taken from the Table 1 in example 1,and to that list we replace the value{D}for simulation of the transient response.It is assumed that the initial concentration in hydrogel isc0=250 mol/L,and the external concentration is considered ascw=600 mol/L.In addition,we have chosen a value D=6.749×10−10m2/s,with the length BC=20 mm,and the height AB=0.5 mm described in the literature in Lucantonio,Nardinocchi,and Teresi(2013).

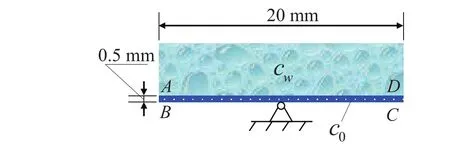
Figure 7:Schematic of the rectangular hydrogel bar.

Fig.8(a)–(d)shows the swelling-induced bending at different times.As time goes on,diffusion will be conducted from a high concentration to a low concentration.The hydrogel bar is absorbed slowly inducing a differential volume expansion which bends downward towards a maximum curvature in subfigure(b).Then,the bar tends to recover its original configuration,and it slowly returns back in subfigure(c).Finally,

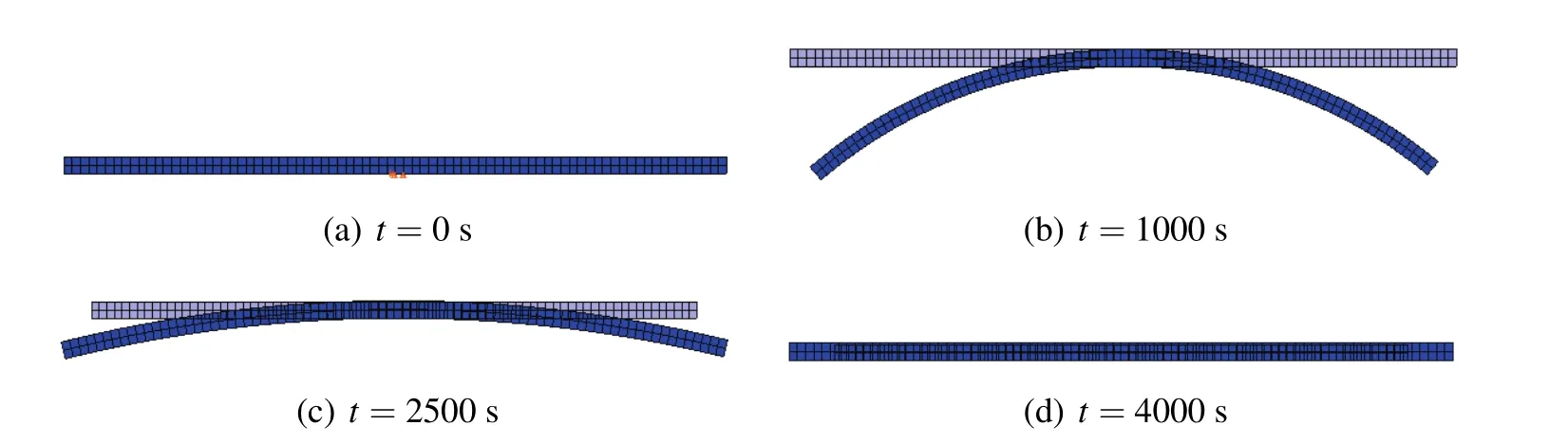
Figure 8:Deformations of the hydrogel bar at different times.

when the timet=4000 s,the system reaches the equilibrium state.Then,a new straight and steady configuration is reached in subfigure(d).The extent to swelling is greater than the configuration in the initial state obviously.It is illustrated that there exactly exists chemo-mechanical coupling process in the rectangular hydrogel bar.The deformation process is consistent with the literature in Lucantonio,Nardinocchi,and Teresi(2013).

3.3 Example 3

Hydrogels have a significant advantage over conventional microfluidic devices owing to their ability to undergo abrupt volume changes in response to the surrounding environment without the requirement of an external power source.In a variety of microfluidic devices in engineering fields,we can utilize chemo-mechanical coupling characteristics to design the hydrogel valve.By changing the concentration,the swelling degree of the hydrogel can be used to adjust the opening and closing of flow in the hydrogel valve.

The third example is considered as shown in Fig.9.There is a rectangular hydrogel plate in which AB,AD,and CD sides are constrained,respectively,and BC side is contact with the solution.The concentration of external solution iscw=500 mol/L,and the concentration inside the hydrogel plate isc0=200 mol/L.Hydrogel parameters are shown in Table 1.

Figure 9:Schematic of the hydrogel valve.

Figure 10:Deformations of the hydrogel valve at different times.

As shown in Fig.10(a)–(d),because the solution concentrationcwis greater thanc0,diffusion will be conducted from a high concentration to a low concentration.As time goes on,the extent to absorption of the solution on BC side increases gradually so as to result in the greater expansion degree.When the timet=4800 s,the system reaches the equilibrium state,as shown in subfigure(d).According to the reversible deformation for hydrogels,this device can be designed as a hydrogel valve,which was shown to be in agreement with the literature in Romero,Dario Arrua,Alvarez Igarzabal,and Hilder(2013).

3.4 Example 4

Next,the fourth example is considered as shown in Fig.11,with a free expansion square hydrogel plate whose four sides are contact with the solution,respectively.We assume that the initial concentration in hydrogel isc0=300 mol/L,andcw=600 mol/L for external concentration.Moreover,the values of material parameters for the list{E,ν,R∗,T}are taken from the Table 1.We have selected a valueD=5× 10−9m2/s,and the side length in initial time is taken as 20 mm shown in the literature from Chester and Anand(2011).

Figure 11:Schematic of the square hydrogel plate.

Fig.12 shows contours of the hydrogel plate after a few different times:(a)0 s;(b)1000 s;(c)2100 s;and(d)3200 s.As time progresses,the initially square specimen is no longer square-this is because of the faster swelling near the corners due to the enhanced fluid flux from the two edges.Finally,the system reaches the equilibrium state in the timet=3200 s,and then the square hydrogel plate turns into a swelling square plate again whose configuration is bigger than original configuration in initial time.The course of deformation is consistent with the literature in Chester and Anand(2011).

Figure 12:Deformations of the hydrogel square plate at different times.

3.5 Example 5

In engineering fields,many functional components are needed to creat microchannels for local flow regulation in microfluidic systems.Here,we can design a hydrogel groove channel to implement the adjustment of local flow.By changing the concentration,the flow inside the groove can be controlled by the extent of expansion or contraction of the hydrogel.

As a final example,we consider a hydrogel groove shown in Fig.13.The solution concentration inside the hydrogel isc0=200 mol/L,and the concentration in groove is considered ascw=550mol/L.Hydrogel parameters areshown in Table1.As shown in Fig.14(a)–(d),whencwis greater thanc0,due to the concentration gradient between the external solution and the internal solution,diffusion will be proceeded from a high concentration to a low concentration.The greater extent to solution absorption on inner sides,the greater the expansion degree is.Whent=4500 s,the system reaches the equilibrium state.By changing the concentration value the hydrogel groove could realize expansion and recovery deformations so as to adjust the flow inside the groove meantime.

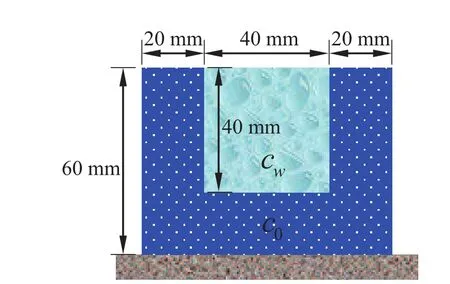
Figure 13:Schematic of the hydrogel groove.

Figure 14:Deformations of the hydrogel groove at different times.

Thus,we can clearly confirm the correctness and accuracy of the user element subroutine UEL programmed by representative numerical examples.In the meantime,with the benefit of articles[Dong,El-Gizawy,Juhany,and Atluri(2014a,b)],the locking phenomenon of lowest order isoparametric elements are effectively avoided,which greatly overcomes the shortcomings of mesh distortion,while maintaining both efficiency and generalization of the chemo-mechanical element developed.Moreover,it is illustrated that the theory of chemo-mechanical coupling proposed and the application of finite element method are greatly convincible.

4 Conclusions

In this paper,starting from the laws of thermodynamics and the definition of the chemical potential,continuum mechanics approach is developed to derive chemomechanical coupled constitutive equations and governing equations during isothermal process.With the Hamilton’s principle,the equivalent integral forms of chemomechanical governing equations and corresponding finite element equations can be derived in chemo-mechanical coupling system.The closeness of the chemomechanical coupling theory and mutual coupling effect between chemical system and mechanical system are validated.

By using the user element subroutine UEL in ABAQUS FE package, several numerical examples of chemo-mechanical coupling behavior are analyzed in hydrogels under different boundary conditions.It is proved that the changes of concentration can cause shape deformation of the hydrogel,and mechanical effect can also induce concentration redistribution.The chemo-mechanical coupling process is actually a process during which the mechanical energy and the chemical energy can be converted to one another.At equilibrium state,the mechanical energy and the chemical energy achieve an overall balance with each other.In addition,the detailed discussions on the numerical examples validate the rationality and effectiveness of the present theory and method.

Although the behavior of deformation has small elastic properties with present theory,the deformation results and processes are similar to the typical examples in several publications related to the numerical implementation with the finite deformation theory.Consequently,we can provide a valuable enrichment and supplement which can assist in the exploration and characterization in research methodology applicable to more general physical and mechanical problems for hydrogels.Next,by complementing and having an even deeper understanding of the knowledge of present theory,hopefully our goal is to enhance present theory to areas of the finite deformation theory,which is the research’s direction.

Acknowledgement:The financial support from the National Natural Science Foundation of China under grants#11172012,#11472020 is gratefully acknowledged.

Ballhause,D.;Wallmersperger,T.(2008):Coupled chemo-electro-mechanical finite element simulation of hydrogels:I.Chemical stimulation.Smart Mater.Struct.,vol.17,no.4,pp.045011.

Bouklas,N.;Landis,C.M.;Huang,R.(2015):A nonlinear,transient finite element method for coupled solvent diffusion and large deformation of hydrogels.J.Mech.Phys.Solids,vol.79,pp.21–43.

Chester,S.A.;Anand,L.(2011):A thermo-mechanically coupled theory for fluid permeation in elastomeric materials:Application to thermally responsive gels.J.Mech.Phys.Solids,vol.59,pp.1978–2006.

Chester,S.A.;Di Leo,C.V.;Anand,L.(2015):A finite element implementation of a coupled diffusion-deformation theory for elastomeric gels.Int.J.SolidsStruct.,vol.52,pp.1–18.

De,S.K.;Aluru,N.R.(2004):A chemo-electro-mechanical mathematical model for simulation of pH sensitive hydrogels.Mech.Mater.,vol.36,no.5,pp.395–410.

De,S.K.;Aluru,N.R.;Johnson,B.(2002):Equilibrium swelling and kinetics of pH-responsive hydrogels:models,experiments,and simulations.J Microelectromech Syst,vol.11,no.5,pp.544–555.

Ding,Z.W.;Liu,Z.S.;Hu,J.Y.;Swaddiwudhipong,S.;Yang,Z.Z.(2013):Inhomogeneous large deformation study of temperature-sensitive hydrogel.Int.J.Solids Struct.,vol.50,no.16–17,pp.2610–2619.

Dong,L.T.;El-Gizawy,A.S.;Juhany,K.A.;Atluri,S.N.(2014a):A simple locking-alleviated 4-node mixed-collocation finite element with over-integration,for homogeneous or functionally-graded or thick-section laminated composite beams.CMC:Comput.Mater.Continua,vol.40,no.1,pp.49–77.

Dong,L.T.;El-Gizawy,A.S.;Juhany,K.A.;Atluri,S.N.(2014b):A simple locking-alleviated 3D 8-Node mixed-collocation C0 finite element with overintegration,for functionally-graded and laminated thick-section plates and shells,with&without z-pins.CMC:Comput.Mater.Continua,vol.41,no.3,pp.163–192.

Duan,Z.;Zhang,J.P.;An,Y.H.;Jiang,H.Q.(2013):Simulation of the transient behavior of gels based on an analogy between diffusion and heat transfer.J.Appl.Mech.;vol.80,pp.041017.

Duda,F.P.;Souza,A.C.;Fried,E.(2010):A theory for species migration in a finitely strained solid with application to polymer network swelling.J.Mech.Phys.Solids,vol.58,pp.515–529.

Filipecki,J.;Sitarz,M.;Kocela,A.;Kotynia,K.;Jelen,P.;Filipecka,K.;Gaweda,M.(2014):Studying functional properties of hydrogel and siliconehydrogel contact lenses with PALS,MIR and Raman spectroscopy.Spectrochim.Acta Part A Mol.Biomol.Spectrosc.,vol.131,pp.686–690.

Flory,J.;Rehner,J.(1943a):Statistical mechanics of cross-linked polymer networks I.Rubberlike elasticity.J.Chem.Phys.,vol.11,pp.512–520.

Flory,J.;Rehner,J.(1943b):Statistical mechanics of cross-linked polymer networks II.Swelling.J.Chem.Phys.,vol.11,pp.521–526.

Gonzalez,J.S.;Ludue na,L.N.;Ponce,A.;and Alvarez,V.A.(2014):Poly(vinyl alcohol)/cellulose nanowhiskers nanocomposite hydrogels for potential wound dressings.Mater.Sci.Eng.C,vol.34,pp.54–61.

Gregorova,A.;Saha,N.;Kitano,T.;Saha,P.(2015):Hydrothermal effect and mechanical stress properties of carboxymethylcellulose based hydrogel food packaging.Carbohydr.Polym.,vol.117,pp.559–568.

Grimshaw,P.E.;Nussbaum,J.H.;Grodzinsky,A.J.;Yarmush,M.L.(1990):Kinetics of electrically and chemically induced swelling in polyelectrolyte gels.J.Chem.Phys.;vol.93,no.6,pp.4462–4472.

Gu,T.;Liu,X.Y.;Chai,W.B.;Li,B.B.;Sun,H.Y.(2014):A preliminary research on polyvinyl alcohol hydrogel:A slowly-released anti-corrosion and scale inhibitor.J.Pet.Sci.Eng.;vol.122,pp.453–457.

Hong,W.;Liu,Z.S.;Suo,Z.G.(2009):Inhomogeneous swelling of a gel in equilibrium with a solvent and mechanical load.Int.J.Solids Struct.,vol.46,no.17,pp.3282–3289.

Hong,W.;Zhao,X.H.;Zhou,J.X.;Suo,Z.G.(2008):A theory of coupled diffusion and large deformation in polymeric gels.J.Mech.Phys.Solids,vol.56,no.5,pp.1779–1793.

Ionov,L.(2014):Hydrogel-based actuators:possibilities and limitations.Mater.Today,vol.17,no.10,pp.494–503.

Kang,B.;Dai,Y.D.;Shen,X.H.;Chen,D.(2008):Dynamical modeling and experimental evidence on the swelling/deswelling behaviors of pH sensitive hydrogels.Mater Lett,vol.62,no.19,pp.3444–3446.

Levine,I.N.(2002):Physical Chemistry.McGraw-Hill Press,New York.

Li,H.(2009):Smart Hydrogel Modelling.Springer-Verlag,Berlin.

Li,H.;Ng,T.Y.;Yew,Y.K.;Lam,K.Y.(2005):Modeling and simulation of the swelling behavior of pH-stimulus-responsive hydrogels.Biomacromolecules,vol.6,pp.109–120.

Li,H.;Ng,T.Y.;Yew,Y.K.;Lam,K.Y.(2007):Meshless modeling of pH-sensitive hydrogels subjected to coupled pH and electric field stimuli:Young modulus effects and case studies.Macromol.Chem.Phys.,vol.208,pp.1137–1146.

Li,H.;Yew,Y.K.(2009):Simulation of soft smart hydrogels responsive to pH stimulus:ionic strength effect and case studies.Mater.Sci.Eng.C,vol.29,no.7,pp.2261–2269.

Li,X.;Fan,D.D.;Ma,X.X.;Zhu,C.H.;Luo,Y.E.;Liu,B.W.;Chen,L.(2014):A novel injectable pH/Temperature sensitive CSHLC/β-GP hydrogel:The gelation mechanism and its properties.Soft Mater.;vol.12,pp.1–11.

Loret,B.;Simoes,F.M.F.A.(2005):framework for deformation,generalized diffusion,mass transfer and growth in multi-species multi-phase biological tissues.Eur J Mech A Solids,vol.24,pp.757–781.

Lucantonio,A.;Nardinocchi,P.;Teresi,L.(2013):Transient analysis of swelling-induced large deformations in polymer gels.J.Mech.Phys.Solids,vol.61,pp.205–218.

Marcombe,R.;Cai,S.Q.;Hong,W.;Zhao,X.H.;Lapusta,Y.;Suo,Z.G.(2010):A theory of constrained swelling of a pH-sensitive hydrogel.Soft Matter,vol.6,no.4,pp.784–793.

Maulvi,F.A.;Soni,T.G.;Shah,D.O.(2015):Extended release of hyaluronic acid from hydrogel contact lenses for dry eye syndrome.J.Biomater.Sci.Polym.Ed.,vol.26,no.15,pp.1035–1050.

Mindlin,R.D.(1974):Equations of high frequency vibrations of thermopiezoelectric crystal plates.Int J of Solids Struct.,vol.10,pp.625–637.

Nawrotek,K.;Tylman,M.;Rudnicka,K.;Balcerzak,J.;Kaminski,K.(2016):Chitosan-based hydrogel implants enriched with calcium ions intended for peripheral nervous tissue regeneration.Carbohydr Polym,vol.136,pp.764–771.

Qin,Q.H.;Yang,Q.S.(2008):Macro-micro Theory on Multifield Behaviour of Heterogeneous Materials.Higher Education Press and Springer,Beijing.

Qian,W.C.(1980):Variational Method and Finite Element Method.Science Press,Beijing.

Rivero,R.E.;Molina,M.A.;Rivarola,C.R.;Barbero,C.A.(2014):Pressure and microwave sensors/actuators based on smart hydrogel/conductive polymer nanocomposite.Sens Actuators,B Chem,vol.190,pp.270–278.

Romero,M.R.;Dario Arrua,R.;Alvarez Igarzabal,C.I.;Hilder,E.F.(2013):Valve based on novel hydrogels:From synthesis to application.Sensors and Actuators B:Chemical,vol.188,pp.176–184.

Roogers,G.E.(1994):Introduction to Coordination,Solid State and Descriptive Inorganic Chemistry.McGraw-Hill Press,New York.

Sagiri,S.S.;Singh,V.K.;Kulanthaivel,S.;Banerjee,I.;Basak,P.;Battachrya,M.K.;Pal,K.(2015):Stearate organogel-gelatin hydrogel based bigels:Physicochemical,thermal,mechanical characterizations and in vitro drug delivery applications.J.Mech.Behav.Biomed.Mater.,vol.43,pp.1–17.

Smith,I.M.;Griffths,D.V.(2003):Programming the Finite Element Method.Electronics Industry Press,Beijing.

Terzaghi,K.;Peck,R.B.;Mesri,G.(1996):Soil mechanics in engineering practice.John Wiley&Sons Press,New York.

Thankam,F.G.;Muthu,J.(2015):Alginate–polyester comacromer based hydrogels as physiochemically and biologically favorable entities for cardiac tissue engineering.J.Colloid Interface Sci.;vol.457,pp.52–61.

Toh,W.;Liu,Z.S.;Ng,T.Y.;Hong,W.(2013):Inhomogeneous large deformation kinetics of polymeric gels.Int.J.Appl.Mech.;vol.5,pp.1350001.

Tongwa,P.;Bai,B.J.(2014):Degradable nanocomposite preformed particle gel for chemical enhanced oil recovery applications.J.Pet.Sci.Eng.,vol.124,pp.35–45.

Ullah,F.;Othman,M.B.H.;Javed,F.;Ahmad,Z.;Akil,H.M.(2015):Classification,processing and application of hydrogels:A review.Mater.Sci.Eng.C,vol.57,pp.414–433.

Wallmersperger,T.;Ballhause,D.(2008):Coupled chemo-electro-mechanical finite element simulation of hydrogels:II.Electrical stimulation.Smart Mater Struct,vol.17,no.4,pp.045012.

Wallmersperger,T.;Kröplin,B.;Gülch,R.W.(2004):Coupled chemo-electromechanical formulation for ionic polymer gels-numerical and experimental investigations.Mech.Mater.,vol.36,no.5–6,pp.411–420.

Wu,B.C.;Degner,B.;McClements,D.J.(2014):Soft matter strategies for controlling food texture:Formation of hydrogel particles by biopolymer complex coacervation.J Phys Condens Matter,vol.26,no.46,pp.464104.

Yang,Q.S.;Liu,B.S.,Meng,L.T.(2009):A phenomenological theory and numerical procedure for chemo-mechanical coupling behavior of hydrogel.CMC:Comput.Mater.Continua,vol.12,pp.39–55.

Yang,Q.S.;Ma,L.H.;Shang,J.J.(2013):The chemo-mechanical coupling behavior of hydrogels incorporating entanglements of polymer chains.Int.J.Solids Struct.,vol.50,pp.2437–2448.

Yang,Q.S.;Qin,Q.H.;Ma,L.H.;Lu,X.Z.;Cui,C.Q.(2010):A theoretical model and finite element formulation for coupled thermo-electro-chemomechanical media.Mech.Mater.,vol.42,no.2,pp.148–156.

Zalachas,N.;Cai,S.Q.;Suo,Z.G.;Lapusta,Y.(2013):Crease in a ring of a pH-sensitive hydrogel swelling under constraint.Int.J.Solids Struct.,vol.50,pp.920–927.

Zheng,A.;Xue,Y.;Wei,D.;Li,S.;Xiao,H.;Guan,Y.(2014):Synthesis and characterization of antimicrobial polyvinyl pyrrolidone hydrogel as wound dressing.Soft Mater.,vol.12,pp.297–305.

1Department of Engineering Mechanics,Beijing University of Technology,Beijing 100124,PR China

2School of Civil Engineering,Hebei University of Engineering,Handan 056038,PR China

3Corresponding authors Email:qsyang@bjut.edu.cn,Tel&Fax:86-10-67396333(QS Yang)