基于ABAQUS的碟式分离机立轴结构模态分析

王 枫，崔建昆

（上海理工大学 机械工程学院，上海 200093）

0 引言

碟式分离机作为一种有效的离心分离设备，广泛应用于化工、轻工、医药和食品等领域。其工作原理是利用转鼓高速旋转产生的离心力，将两种不同密度的物质所组成的混合物（液－液、固－液）分离开来［1］。分离机的转鼓是实现物料分离的主要部件，转鼓安装在立轴上，立轴由上、下两个滚动轴承支撑，转鼓由立轴带动高速旋转，因此立轴承受着巨大的载荷［2］。本文基于ABAQUS对立轴进行结构模态分析，确定其前10阶固有频率和模态振型，并分析其振动特性。

1 碟式分离机的分离原理

碟式分离机是立式离心机，转鼓装在立轴上端，通过传动装置由电动机驱动而高速旋转。转鼓内有一组互相套叠在一起的碟形零件——碟片，碟片与碟片之间留有很小的间隙。悬浮液（或乳浊液）通过位于转鼓中心的进料管进入转鼓，当悬浮液流过碟片之间的间隙时，固体颗粒（或液滴）在离心机作用下沉降到碟片上形成沉渣（或液层）。沉渣沿碟片表面滑动而脱离碟片并积聚在转鼓内直径最大的部位，分离后的液体从出液口排出转鼓。碟片的作用是缩短固体颗粒（或液滴）的沉降距离、扩大转鼓的沉降面积，转鼓中由于安装了碟片而大大提高了分离机的生产能力。积聚在转鼓内的固体在分离机停机后拆开转鼓由人工清除，或通过排渣机构在不停机的情况下从转鼓中排出。分离机分离原理示意图如图1所示。

2 建立模态分析的数学模型

由动力学分析理论可知，物体的模态参数由其固有频率和振型组成，这两个参数主要由物体的结构、质量和刚度决定。因此，可根据自由振动基本微分方程建立模态分析的数学模型。自由振动的基本微分方程为：

其中：M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；X为位移向量；t为时间；F（t）为作用力向量。

由于本文所研究对象立轴的阻尼较小，其对固有频率和振型的影响较小，故将其阻尼忽略不计，即C＝0。因此，当F（t）＝0时，式（1）变为：

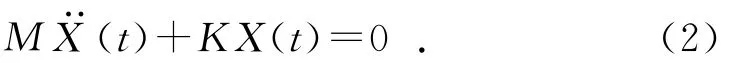
立轴做自由振动时，其上的各节点作简谐振动，各点的位移为：

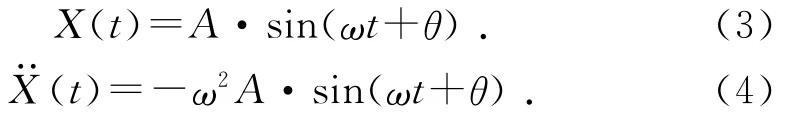
其中：A为自由振动时各节点的振幅向量；ω为固有频率。将式（3）、式（4）代入式（2）得：

式（5）是关于广义特征值ω2的n次方程。

图1 分离机分离原理示意图

3 建立立轴的三维模型

立轴长度为1 213mm，最粗部分直径为Φ90 mm，最细部分直径为Φ30mm，空心直径为Φ22mm。

本文采用Autodesk公司开发的三维设计软件Inventor 2012建立立轴的三维模型，模型完全依照图纸要求建立，无简化，因此在很大程度上会减小计算和分析误差。立轴的三维模型如图2所示。

4 结构模态分析

4.1 网格划分

立轴模型导入ABAQUS后，在划分网格前需要创建材料、定义装配件、定义分析步和添加边界条件。本立轴的材料采用0Cr18Ni9Ti，其密度为7 850kg/m3，弹性模量为1.99×1011Pa，泊松比为0.3。首先，进入属性模块，设置好材料后，创建截面属性并将材料赋予截面属性；其次，进入装配模块，创建部件的实例；然后，进入分析步模块，创建分析步，分析步类型选择“线性摄动：频率”，选择特征值求解器为Lanczos，定义“请求的特征值个数”为10，即分析立轴前10阶固有频率和振型；最后，进入载荷功能模块，由于只是对立轴进行模态分析，故不需要定义载荷，只需定义边界条件，“类别”选择“位移/转交”，选择几何约束为“U1，U2，U3，UR2，UR3”。在完成以上设置后，对立轴进行网格划分，单元类型采用C3D10十节点二次四面体单元，共有13 919个单元实体，23 453个节点。立轴有限元模型如图3所示。

4.2 模态分析

结构的振动可由各阶固有频率与对应振型的线性组合来表示，而其中低阶振动对结构的动力影响程度比高阶振型大。图4为立轴前10阶模态振型。从图4可以看出，扭转弯曲振型对立轴影响程度较大，立轴的顶部、下部和中部为其薄弱环节，可适当加强该部位的支撑。

图2 立轴的三维模型

图3 立轴有限元模型

图4 主轴的前10阶模态振型图

表1为立轴前10阶模态分析结果。由表1可以看出，第9阶固有频率下的振幅最大，为1.179mm。为确保碟式分离机稳定运行，其工作转速应避开各阶固有频率下对应的转速。

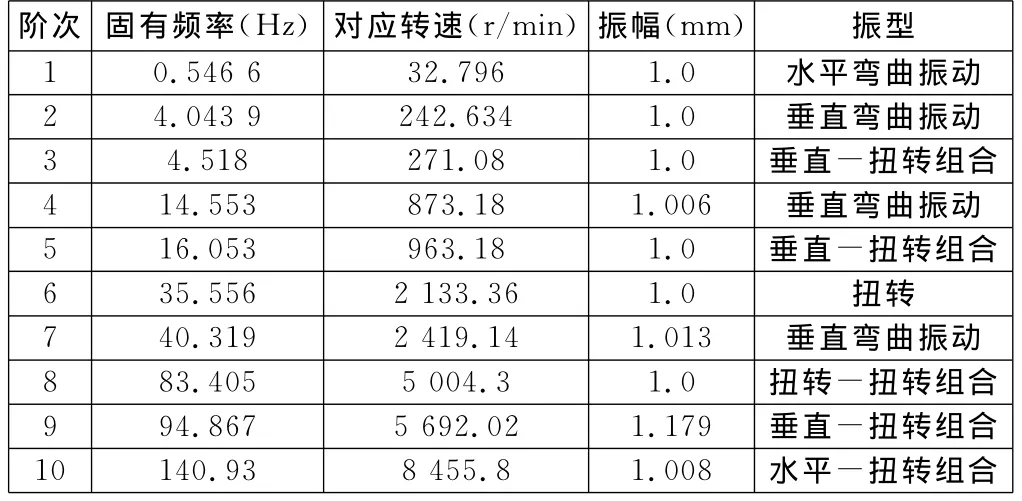
表1 立轴模态分析结果

5 结论

本文利用ABAQUS有限元分析软件对碟式分离机中的立轴进行结构模态分析，模拟仿真出立轴的前10阶固有频率和相对应的振型。分析结果表明，立轴在高速旋转过程中受离心力比较大，其主要振动振型为垂直弯曲振动和扭转，应对其薄弱环节加强结构支撑。本文的分析结果为立轴的优化设计提供了依据，为以后的动力学分析打下了基础。

［1］韩捷，梁利华.碟式分离机转鼓锁环的有限元应力分析［J］.浙江工业大学学报，2002，30（5）：460－463.

［2］贺世正，王东辉.碟式分离机立轴系统结构参数对临界转速的影响［J］.农业机械学报，2005，36（7）：57－60.

［3］贺世正，王东辉.陀螺效应对碟式分离机立轴系统动态特性的影响分析［J］.流体机械，2004，32（10）：18－21.

［4］刘延柱，陈文良，陈立群.振动力学［M］.北京：高等教育出版社，1998.

［5］马晓峰.ABAQUS 6.11中文版有限元分析从入门到精通［M］.北京：清华大学出版社，2013.