航空器蒙皮维修圆补片小挠度弯曲力学分析❋

董艇舰，陈 瑾，丁华鹏

（中国民航大学 工程技术训练中心，天津 300300）

0 引言

半硬壳航空器是由杆件、桁条和隔框构成骨架，外覆蒙皮承受气动载荷。由于航空器各部分受力情况复杂，不同区域维修方法各不相同，蒙皮维修是航空器结构修理的主要任务。目前基本按照SRM（Structure Repair Manual）结构修理手册提供的通用计算公式设计蒙皮。经验公式法依据受损材料的体积、远超出极限强度的经验假想强度和工作强度的比例关系，估测需要的加固点数，即铆钉数，推测出补片的尺寸。经验公式算法扩大了补片的结构尺寸，增加了维修工作量和成本，同时扩大了铆接面积，显然该方法不是精确的力学方案，而是采用大冗余度保证安全的简化维修方案。该方法增加了维修工作量和成本，由于大面积的铆接，还影响了机体的结构强度，特别是机体结构受限的尺寸空间，会导致普通维修无法进行，影响航空器运营［1］。本文运用广义内力素分析方法［2］，通过精确力学［3］计算确定圆补片小挠度弯曲构型，量化制定补片的尺寸参数、工艺参数和力学参数，实现补片的数字化优化设计和制作。

1 广义内力素薄板［4］模型

蒙皮维修的圆形补片面积一般较小，曲率很小，可看作平板［5］（此处限于小曲度区域）。本模型设定载荷垂直于板面，则补片为二维结构弹性板，可产生拉压、剪切、弯曲和扭转变形，按薄板壳理论建立的蒙皮补片单元模型如图1、图2所示。按照广义内力素性质，在坐标系中设T1和T2为面内拉力，T12和T21为面内切力，Q1和Q2为横剪力，均为中面单位长度上作用的力；M1和M2为弯矩，M12和M21为扭矩，均为中面单位长度上作用的力矩。

图1 蒙皮补片单元受力模型

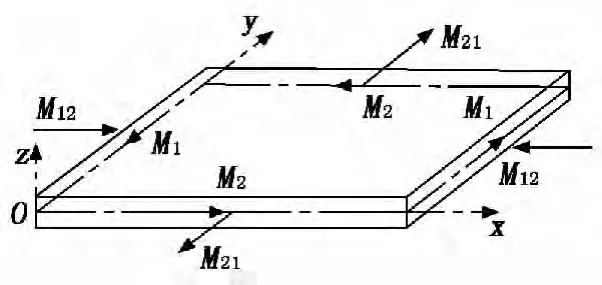
图2 蒙皮补片单元受弯矩模型

设板厚为2h，当板横面上作用平行于中面的正应力σ1，σ2和剪应力τ12时，力和力矩的表达式为：

此外还有横向剪应力τ1z和τ2z的合力：

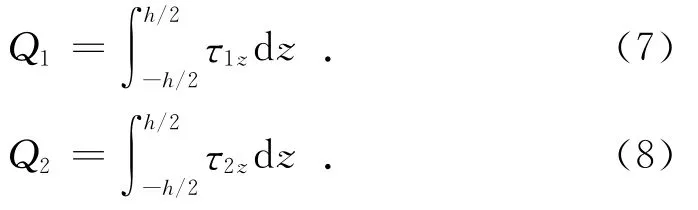
式（1）～式（8）通过面内拉力、剪力、弯矩和扭矩构成广义内力素，精确表达了平板内所有力的分布情况。

2 补片小挠度弯曲微分方程及其解

当薄板受力发生弯曲时，沿x轴方向的位移u、沿y方向的位移v和挠度ω有下列几何关系：

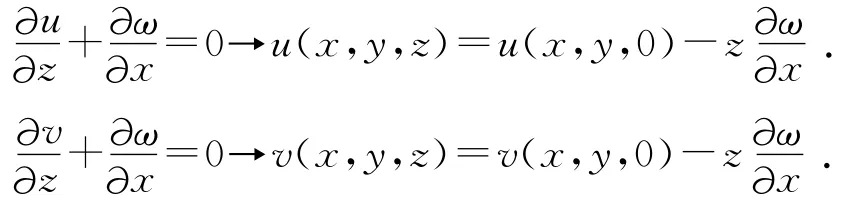
忽略中面变形，可得板的面内应力与板的法向位置的二阶导数，即应变εx，εy，γxy：

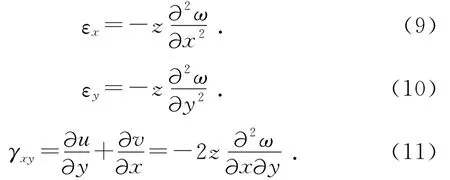
结合广义胡克定律可知板小挠度弯曲的弹性关系（其正方向的定义见图1、图2）：

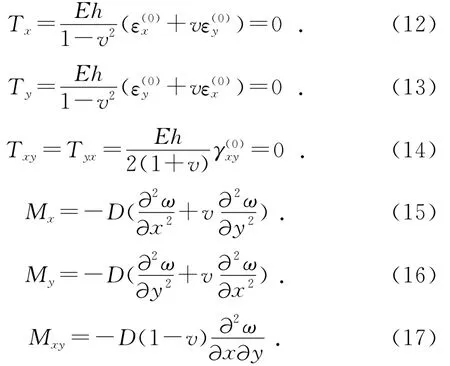
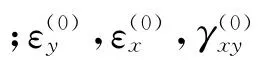
弯曲的平衡方程通过板微元体平衡获得。已知图2为边长dx和dy，厚度为2h的板微元体［6］，板面法向载荷为p（x，y）。则由力矩平衡条件可得：

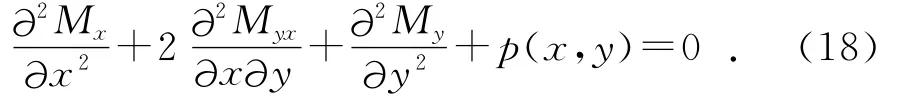
将式（15）～式（17）代入式（18）得：

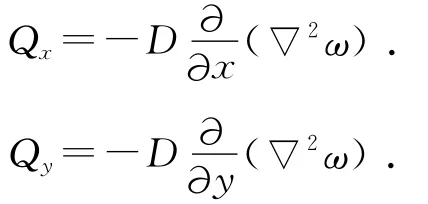
对于轴对称载荷作用的圆板，在柱面坐标内x＝y＝r，则公式（19）变为：

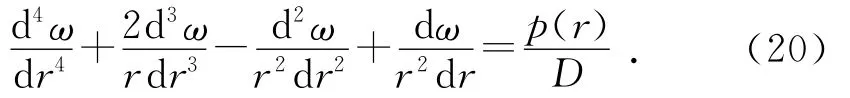
解式（20）可得：

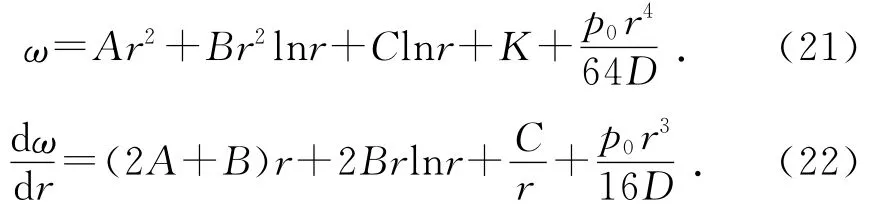
其中：A，B，C，K均为待定系数；p0为均布载荷。同理可以求得对应的弯矩Mr和Mθ，扭矩Mrθ，横剪力Qr和Qθ：

3 圆补片小挠度弯曲力学分析

针对蒙皮圆补片，周边认定为简支，受均布载荷p0作用，可以求得圆补片的挠度与应力。结合柱面坐标系下的边界条件可得：

（1）r＝0时，ω有界，C＝0，无集中力作用，则B＝0。

（2）r＝R（R为补片半径）时，ω＝0，Mr＝0，将其分别代入式（21）和式（23）得：AR2＋K＋p0r4/（64D）＝0，－2D（1＋v）A－（3＋v）p0R2/16＝0。

由此求得柱面坐标系下对应的挠度ω、弯矩与剪力：

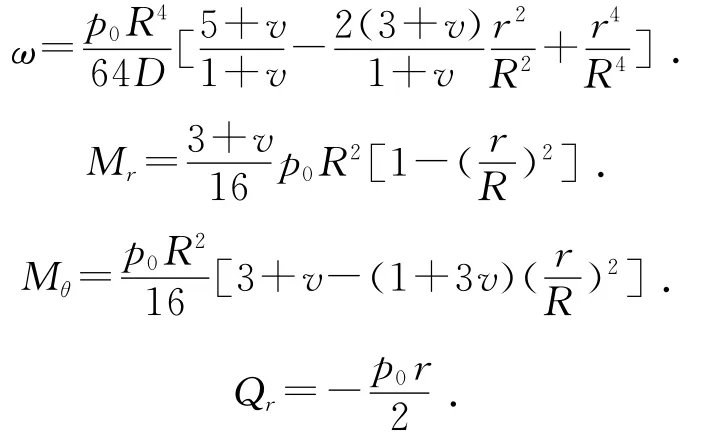
并可得板中应力：

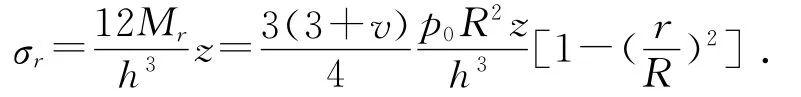
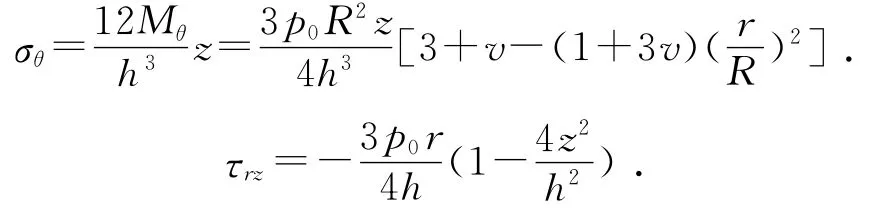
σr，σθ和τrz的分布状况如图3和图4所示。

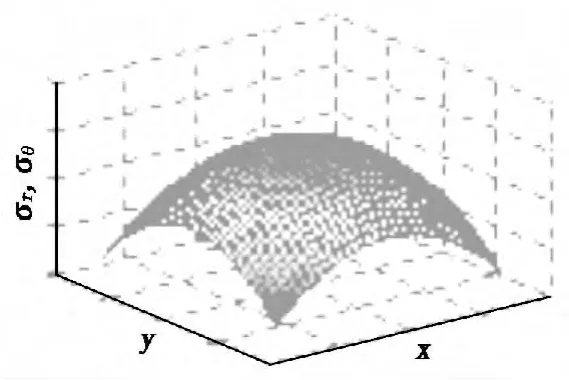
图3 σr，σθ 的分布状况

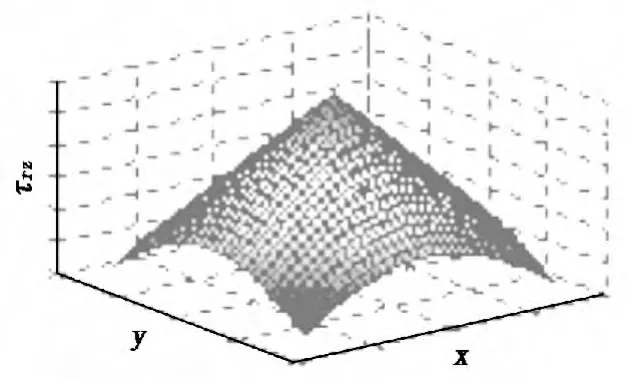
图4 τrz的分布状况

由图3和图4可知，圆补片的正应力和剪切力在中心处最大，正应力分布为球冠型，中心区域最大，近似抛物线分布；剪切力分布呈圆锥型，即线性增长。在中心处，即当r＝0时：

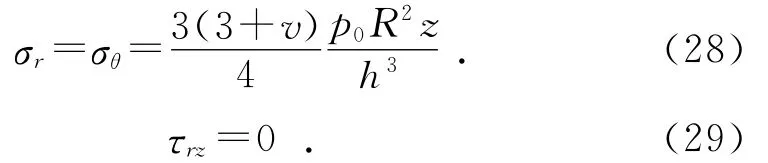
在边缘处，即r＝R时：

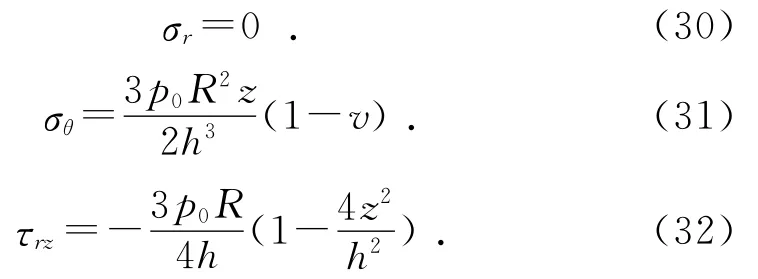
4 圆补片设计的优化方法［7］

传统的维修中，补片尺寸是按照铆钉5d间距和2d边距（d为铆钉直径）排布规则推算的，一般情况余度很大，安全系数高，但工作量也大，维修成本高。

应用挠度力学分析方法，量化计算安全范围内补片的精确尺寸，再通过边距规则修正尺寸，即可最优化地得到补片的设计尺寸。由式（31）、式（32）可得到由正应力与切应力来确定的补片尺寸，即：

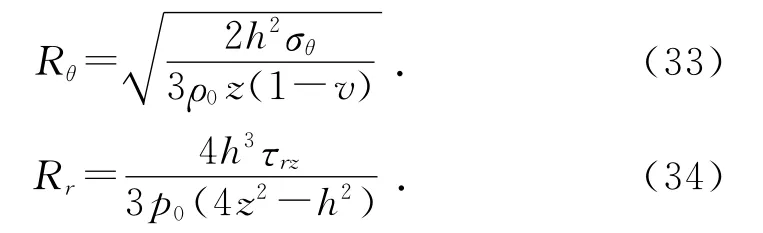
因此只须确定补片需要负荷的最大压力和剪力，代入补片的结构参数，即可计算出2种补片的半径尺寸，选择最大的R值作为理论计算尺寸，按照边距规则排列铆钉，最外圈按照上限原则保证最大覆盖取整方法即可完成工艺尺寸的制定。

该优化方案以力学基本理论为指导，量化地确定了航空器蒙皮孔型损伤维修中的补片尺寸，有效减少了维修成本，为航空器蒙皮维修指明了发展方向。但优化方案中具体参数的确定需要大量的实验数据，该方案虽然得到了量化公式，但如果想要在实际应用中实现，还需要大量的可靠性验证才行，这有待进一步的研究讨论。

［1］任仁良.维修基本技能［M］.北京：清华大学出版社，2010.

［2］薛明德，向志海.飞行器结构力学基础［M］.北京：清华大学出版社，2009.

［3］王敏中，王炜，吴际可.弹性力学教程［M］.修订版.北京：北京大学出版社，2011.

［4］刘鸿文.材料力学［M］.北京：高等教育出版社，2011.

［5］崔延，屠凤莲.不规则形状薄板的平面应力分析［J］.机械设计与制造，2012（8）：218－219.

［6］Xu B X，Wang M Z.The quasi eshelby property for rotational symmetrical inclusions of uniform eigencurvatures within an infini template［J］.Proc.Roy.Soc，2005，A461：2899－2910.

［7］J Cutle. Understanding Aircraft Structures ［M ］.Blackwell Publishing Ltd：Oxford，Malden，MA，2005.