风沙跃移运动的数值模拟❋
2015-12-31黄新成王旭峰蒋建云何欢欢
刘 博,黄新成,王旭峰,蒋建云,何欢欢
(塔里木大学 机械电气化工程学院,新疆 阿拉尔 843300)
0 引言
20世纪30年代,美国和加拿大西部大草原的沙尘暴灾害受到全世界的高度重视。基于这次沙尘暴灾害,Bagnold[1]将风沙运动作为一个空气动力学来研究,于1941年发表了关于风沙物理学的著名论著。他通过利比亚沙漠中的野外观测和实验室风洞试验确定了沙粒运动的力学机制,指出了沙粒的运动主要发生在0m~1m的高度范围内,在10cm~20cm的高度范围内较为集中[2]。在他的著作中,深刻地描述了未起沙地表和起沙地表上方的风速剖面、跃移沙粒的运动轨迹、沙粒运动的临界风力、风沙的单宽输沙率等物理学问题,对理性认识风沙运动具有重要意义。
本文采用硬球模型建立了单颗沙粒的运动模型,并充分考虑颗粒间的碰撞作用,模拟了沙粒速度随高度的变化以及输沙量随高度的分布状况。
1 沙粒跃移运动模型
1.1 流体相控制方程
近地层风沙运动满足纳维-斯托克斯方程,矢量式为:
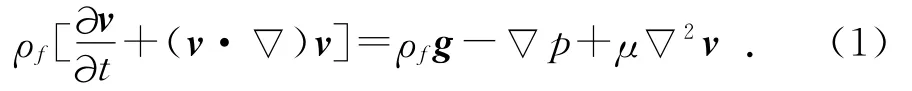
其中:t为运动时间;ρf为流体密度;g为重力加速度;μ为黏性系数;p为流体压力;v为x方向风速。记τf=μ▽v,为雷诺切应力,则式(1)变形为:
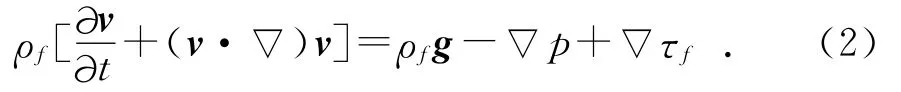
由于沙粒粒径较大,且较为干燥,沙粒间的液膜黏结力和静电力可忽略不记,沙粒近似为无黏性流体,又因为跃移层中的沙粒拖拽力可以改变风速分布,其对风速的作用可以近似认为是纳维-斯托克斯方程式添加一个修正项Fdray,即:

其中:ΔV为控制体的体积;Fdray为单颗粒所受拖拽力;fdray,i为控制体内第i个颗粒对沙粒的拖拽力;n为控制体内的颗粒数。
1.2 颗粒碰撞模型
颗粒间碰撞的瞬时性是硬球模型的基本思想,颗粒本身在碰撞过程中是不会发生变形的。根据动量守恒原理得到颗粒碰撞后的运动状态模型的突出特点是:通过给定摩擦因数和恢复系数就能够求出碰撞后的颗粒运动速度,此模型适合低浓度颗粒流的计算。
沙粒在运动过程中不断地与其他沙粒发生碰撞,因此通常采用离散颗粒动力学模型。在两次碰撞之间,每个沙粒在拖拽力和重力的作用下运动。由于碰撞时动量的交换是瞬时完成的,其冲力远大于气流拽力、重力和沙粒间的摩擦力,因此仅考虑瞬间碰撞引起的速度变化即可。根据沙粒在不同运动过程中的受力特点,可以把运动分解为受冲力支配的瞬时碰撞过程、受拖拽力和重力控制的非瞬时漂移过程,从而建立了对沙粒-沙粒的离散颗粒动力学模型[3]。
沙粒是球形刚体,不考虑沙粒的变形,碰撞为两刚性体相碰撞,且发生在质心面上,碰撞点仅为两颗粒的接触点,如图1所示,其中,x轴和y轴分别沿法向和切向,Px,Py分别是x和y方向的冲量。碰撞过程中产生瞬时法向和切向冲量,两沙粒动量和角动量均守恒。
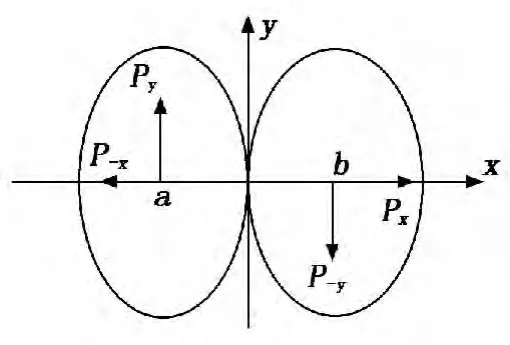
图1 沙粒碰撞示意图
1.3 跃移沙粒的受力分析
在非均匀不规则床面上,风带动沙粒起动,以一定的角度起跳后又会以一定的角度落地,在落地时由于存在一定的速度和冲击动能,会发生冲击颗粒的反弹,同时床面静止颗粒被溅起。与此同时,颗粒间动量向深层颗粒逐渐传递,直到最后被耗散掉。
图2为非均匀不规则床面上颗粒冲击起动过程。由图2可以清晰地看出,在不均匀床面上,颗粒以一定的速度冲击然后起跳,并且带动其他颗粒起跳,还有一部分颗粒能量最终被消耗掉。床面与颗粒碰撞作用力的传递过程如图3所示。表层颗粒获得能量后离开床表面,通过反作用力而起跳,而深层颗粒将逐渐被碰撞将作用力耗散掉[4]。

图2 非均匀不规则床面上颗粒冲击起动过程

图3 颗粒与床面碰撞作用力传递过程
沙粒在跃移的过程中所受上升力和Magnus力远小于重力和拖拽力,可以忽略不计。任一颗沙粒的运动方程可用牛顿第二定律表示为:

其中:m为单颗沙粒质量;a为沙粒加速度;W为单颗沙粒所受重力。进而可分析得出沙粒跃移运动方程为[5]:

其中:ρ为空气密度;D为沙粒直径。
2 输沙率的研究
气流单位时间通过单位宽度或面积所搬运沙量叫做风沙流的输沙率。影响输沙率的因素很多,其值主要取决于风力的大小、沙粒粒径和形状、沙粒比重,而且还受沙粒的湿润度、空气稳定度及地表状况的影响。
2.1 沙粒速度随高度的变化
图4为沙粒速度随高度的变化规律。由图4可以看出,沙粒速度随高度的增加而增加,近似对数函数曲线。这是因为风速随高度的分布近似对数函数,沙粒的水平速度方向与风速相同,在风力的拖拽作用下移动,沙粒的水平速度与风速变化的趋势相近,故随高度的增加速度呈对数函数增加,这个规律与风洞试验测出的沙粒速度分布规律相近。
2.2 输沙量随高度的变化
图5为输沙量随高度的分布规律。由图5可以看出,输沙量随着高度的降低呈指数函数下降。Dong等人[6]用集沙仪测量的输沙量分布也是呈指数规律衰减,与上述理论分析一致,理论和实践皆可以证明输沙量和高度之间存在指数关系。
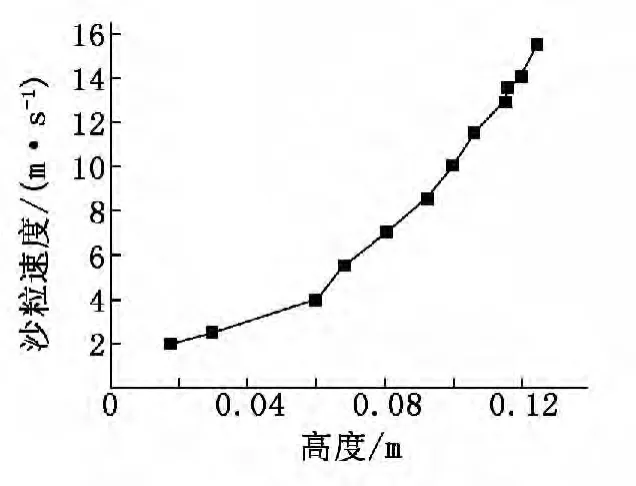
图4 沙粒速度随高度变化规律

图5 输沙量随高度分布规律
3 结论
利用纳维-斯托克斯方程推导了风沙流体相控制方程,采用离散单元法和硬球模型分析了颗粒碰撞原理和受力状况,模拟出沙粒的运动速度随沙粒的水平高度增加而增加,并且呈对数函数规律增加,得出输沙量随高度呈指数衰减的规律。该结论有助于进一步了解沙粒运动轨迹、沙床形态以及风沙运动机理,对治理风沙具有重要意义。
[1]王涛,陈广庭,钱正安,等.中国北方沙尘暴现状及对策[J].中国沙漠,2001,21(4):322-327.
[2]董飞,刘大有,贺大良.风沙运动的研究进展和发展趋势[J].力学进展,1995(3):368-391.
[3]孙其诚,王光谦.模拟风沙运动的离散颗粒动力学模型[J].泥沙研究,2001(4):12-18.
[4]亢力强,郭烈锦.软球模型风沙跃移中颗粒与多粒径床面碰撞的数值模拟[J].工程热物理学报,2006,27(1):83-84.
[5]姚建林.沙粒空中碰撞对风沙跃移运动的影响[D].兰州:兰州大学,2006:21-30.
[6]亢力强,郭烈锦.风沙运动的DPM数值模拟[J].工程热物理学报,2006,27(3):441-444.
