基于BDS/INS动动组合相对定位技术的试验

徐冠楠，汪捷

（海军工程大学，武汉 430033）

0 引言

由于卫星导航与惯性导航系统都可以各自分别进行导航定位，所以当导航接收机进入隧道，室内或者高楼的狭窄街道等地，其在短时间内无法接到卫星信号时，仍可以在短时间内通过惯性导航定位系统进行较为精确的定位，惯性导航的定位结果也能够使导航接收机进行较快的跟踪和捕获。本文重点是针对卫星观测条件的不良条件下如何保证GNSS定位精度的问题，鉴于惯性导航短时间高精度的特点，提出采用惯性信息进行辅助测距。

1 BDS/INS动动定位模型

BDS/INS组合导航系统的状态方程是将北斗卫星导航系统误差状态量与惯性导航系统误差状态量联合起来，共同作为组合导航系统的状态量。在BDS双频差分载波相位与惯导信息组合模型中，关键步骤是BDS模糊度的有效解算，若不能正确解算出模糊度，在后续的滤波器中就只能以差分伪距和多普勒输入，进而无法解算出高精度的模糊度，达不到高精度要求。下面本文将着重讨论在可见卫星数目大于4颗以及小于等于4颗两种观测情况下模糊度解算的具体方法：

1.1 卫星数大于4颗

当可见卫星数目大于4颗时，组合系统的模糊度解算可以采用常规的模糊度方法进行解算。具体过程为：在BDS/INS组合中，可以利用IMU信息辅助解算模糊度，将INS导航结果的三维坐标作为一个数据源和BDS伪距一起进行模糊度浮点解解算，以此有效地减小模糊度初始搜索空间。在此过程中由于加入INS导航结果，其解算的模糊度浮点解精度高于单独使用伪距解算结果的精度。

现假设INS系统导航输出的三维空间位置为RINS，BDS伪距观测方程在此结果处线性化得到双差定位方程如下：

其中，Lρ为观测值，[dXdYdZ]为大地坐标系下三方向矢量的分量，B为观测系数，eρ为伪距观测噪声及误差。

鉴于紧密组合方式，将INS系统作为参考系统，也就是说，将INS导航输出的位置作为参考位置，以INS在此导航位置作为虚拟观测点，在此观测点可以形成如下的观测方程：

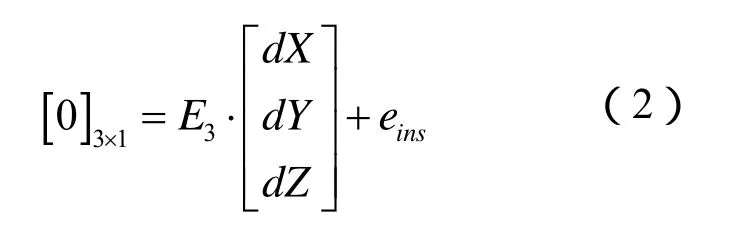
其中，E3为3×3维单位矩阵，eins为观测噪声。

将上述方程联立，可以得到伪距和INS综合定位方程：

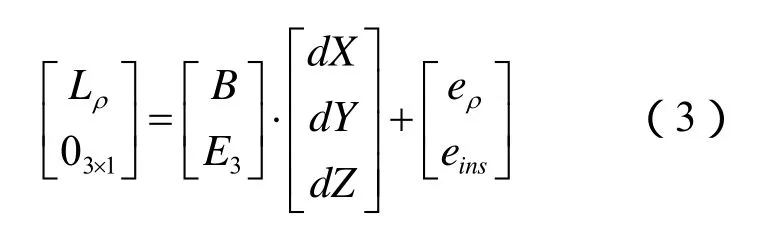
此时，后续步骤的一种方法是对上式进行最小二乘解算，利用解算结果反算出模糊度初始的浮点解。另一种方法是将BDS载波相位观测方程在INS导航结果处进行线性化，得到如下双差载波相位定位方程：

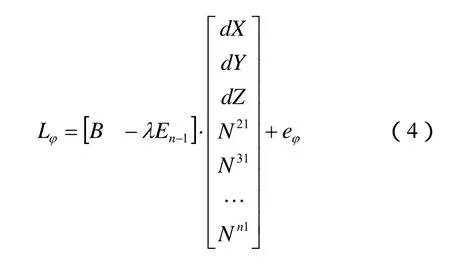
利用式（4）同样可以解算得出模糊度浮点解的最终方程：

需要说明的是，无论采取上述哪种方式，浮点解结果解算相同。

1.2 卫星数小于等于4颗

上述情况均基于可见卫星数目大于4颗，既可以利用码伪距、载波相位单独结算，也可以利用INS辅助解算的情形。当卫星数小于等于4颗时，由于传统的观测方程未知数大于方程个数，因此无法利用常规的OTF方法进行模糊度解算，着重对此情形进行分析和研究。

设INS导航输出的三维空间位置为Rins，在可见卫星数目小于4颗时，同样可以得到如下形式的定位方程：

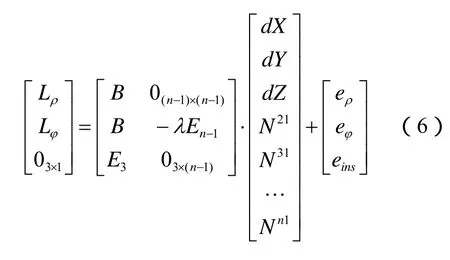
由式（6）可得模糊度浮点解如下：

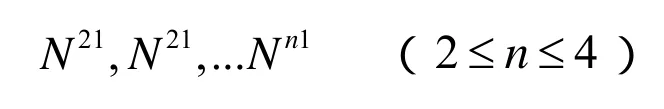
现假设惯导输出的姿态矩阵为Cb，RIb为利用惯导输出信息解算得到的基线向量，Rb为两个动态站搭载的卫导接收机天线构成的基线在坐标系中的向量，φ为惯导平台误差角向量。利用本文算法得出的由惯导输出信息求得的基线向量为：

通过组合滤波输出的方差阵可以得出利用惯导位置计算的基线向量方差阵为：

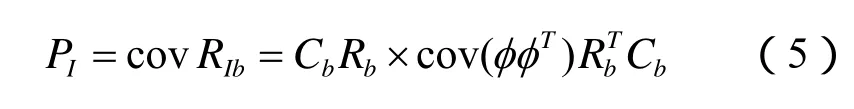
因此由双差载波相位观测方程以及惯导输出的基线向量和方差矩阵得出模糊度向量为：

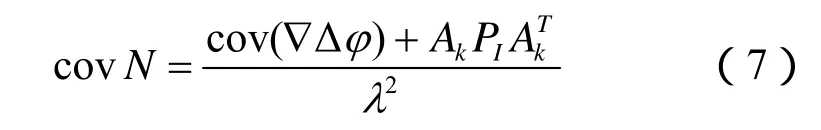
表1给出了试验过程中，利用差分BDS/INS组合系统在观测卫星小于4颗时的模糊度解算结果统计。

2 试验验证

方案设计：为了测试动动组合相对定位系统精度性能，2015年2月10日于武汉市解放大道古田路一段足够长的15°斜坡上开展试验。试验前，将搭载有捷联惯导平台和卫导（天线、接收机等）组合系统的车辆作为移动站，搭载有卫导设备的车辆作为移动基准站进行动动相对测试，如图1所示，以此验证系统相关精度及性能。

表1 差分BDS/INS卫星数小于等于4颗时模糊度解算结果统计情况

图1 两站车辆及设备搭建示意图

试验方法：试验过程中，为了尽量模拟实际应用环境，移动站车辆从一个15°左右的坡上向下驶向移动基站车辆，移动基站车辆在坡 下做低速运动。试验过程中，设置接收机的定位模式为BDS/GPS组合定位，卫星截止高度角设置为15°，数据更新频率为1Hz，整个试验过程为30min。正常行驶时的车速大约在30～40km/h。

试验结束后，对BDS和INS分别输出的原始数据运用本文的组合算法进行处理，对处理后的结果取中间180个历元说明，得到的相对基线矢量在以动态基准站为基准的东北天坐标系下的分量（E、N、U）和长度（L）如图2所示。

由于在短基线情况下，GPS定位精度较高，可以将GPS/INS组合数据解算的相对基线结果作为标准值。现为测试IMU信息后的处理方法的定位精度，将相同历元解算的单BDS基线结果和BDS/INS解算的基线结果分别与Grafnav软件处理的结果进行比较，偏差图如图3所示。

图2 东北天坐标系下相对位置矢量坐标及长度变化图

图3 东北天坐标系下的相对位置矢量坐标及长度偏差

由图可见，在100到120历元这段时间内，偏差较大，经过判断，初步原因可能是由于在试验过程中，信号失锁或者质量较差引起的原始数据处理的偏差。

对整个过程中的所有试验数据进行95%置信概率统计精度分析，得到水平、垂直和三维定位精度。首先为达到95%的置信度，需要设定92.5%～97.5%的区间，经过正态表查询可以得到对应的常数C值为2.675。假设该组数据的方差为S2，均值为，数据总长度为n，则有对应的置信区间为：

其中，n=180，分别将数据利用上式求解出N、E、U向的精度如表2所示。

表2 BDS/INS动动组合系统定位精度结果表（单位：m）

由表2可见，组合系统水平定位精度为0.224m，垂直定位精度为0.328m。

3 总结

本文通过分析不同卫星观测条件下的定位问题，分别研究相应条件下的模糊度求解模型和方法，着重对卫星数目不足时利用惯性信息辅助解算模糊度做了研究，给出了紧组合求解模糊度的方法。在此基础上，搭建了组合试验系统，进行了组合系统的动动定位测试，通过试验数据表明，经过IMU信息辅助后的定位精度有一定的提高，BDS/INS水平定位精度为0.224m，垂直定位精度为0.328m，在一定精度要求下能够满足绝大部分精度需求的应用，同时验证了本文方法的有效性。

[1]喻国荣.基于移动参考站的GPS动态相对定位算法研究:博士学位论文[D].武汉:武汉大学,2003.

[2]俞文伯,高国江.单频GPS动态相对定位模糊度逼近/搜索解法[J].北京航空航天大学学报,2002,28（2）.

[3]孙红星.差分GPS/INS组合定位定姿及其在MMS中的应用:博士学位论文[D].武汉:武汉大学,2004.

[4]喻国荣.动对动GPS相对定位系统中整周模糊度求解[J].中国铁道科学,2003,24（4）.

[5]胡丛玮,刘大杰.单历元确定GPS整周模糊度的分析[J].南京航空航天大学学报,2001,33（3）.

[6]刘根友,朱耀仲,韩保民.GPS单历元定位的阻尼LAMBDA算法[J].武汉大学学报（信息科学版）,2004,29（3）.

[7]Guochang Xu.GPS Theory,Algorithms and Applications[M].Springer-Verlag Berlin Heidelberg New York,2003.

[8]Jon Glenn Gjevestad Svendsen.Some properties of decorrelation techniques in the ambiguity space[J].GPS Solutions,2006(10):40-44.

[9]Huming Wu.On-the-fly ambiguity resolution with inertial aiding[D].Calgary,Canada:University of Calgary,2003:6 0-73.