可分离式构型深空探测器最优分离点评价方法
2015-12-31侯延林
尤 伟,侯延林
(1.上海卫星工程研究所,上海 200240;2.上海市深空探测技术重点实验室,上海 200240)
0 引言
航天器的变轨能力一般可用其能提供的速度增量Δv表示。不同任务对航天器变轨能力的需求各异,近地低轨卫星<0.1km/s,地球静止轨道卫星<0.5km/s,月球环绕探测器约1.7km/s,火星环绕探测器约3km/s,木星探测器约6km/s,其中深空探测任务对航天器变轨能力有较高的要求。为适应深空探测任务速度增量需求大、探测器重量资源有限的特点,出现了分离式构型的深空探测器。分离式航天器机动能力的优势主要源于推进剂耗尽、舍弃多余干重后形成的速度增量增加,即在发射质量与推进剂携带量一定的前提下,采用分离式设计的航天器可提供更大的速度增量,从而提高了航天器的机动能力和快速响应能力[1]。
虽然分离式航天器理论上的变轨能力更强,但相对一体式航天器,分离式航天器需增加额外的分离装置、推进系统管路等重量开销,因此工程应用中须在统筹考虑分离式设计带来的优势与资源消耗后,做出客观评价。分离式构型在运载火箭领域获得了广泛应用,多级运载火箭通过及时分离燃料耗尽后的推进级降低火箭重量,增强运载能力。在深空探测任务中,美国麦哲伦号金星探测器、中俄联合福布斯-土壤火星探测器也均采用了分离式设计。目前分离式航天器对分离界面与分离点选取的主要依据是任务对速度增量的需求,如GEO卫星的远地点发动机、麦哲伦号探测器的推进舱和福布斯-土壤号探测器的上面级。现有分离界面的选取主要面向工程实施与分系统划分的需要,缺乏有效的数学模型定量评价分离式设计的效果。
本文以火星探测任务为背景,通过对推进系统、分离装置重量等的初步数学建模,以有效入轨质量为评价标准,开展可分离式构型深空探测器最优分离点的分析与设计,为我国未来深空探测器的设计提供参考。
1 数学建模
用经典齐氏火箭公式建模,

式中:m0,mf分别为航天器机动前初始质量和机动后终质量;Isp为推力器比冲;g0为当地重力加速度[2]。
对某一特定的航天任务,Δv为常值。分离式航天器可通过多级推进实现该速度增量。若分离级数为2级,则有
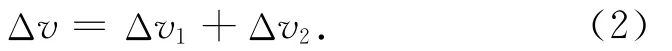
式中:Δv1为一级推进系统需提供的速度增量;Δv2为二级推进系统需提供的速度增量。根据齐氏公式,一级推进系统所需的燃料质量
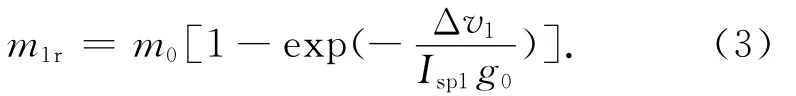
式中:Isp1为一级推进系统比冲。
装载质量为m1r燃料的一级航天器所需干质量m1g通常需经各分系统初步设计后得到。为便于分析,本文用函数f1表示,即

一般,燃料量越大m1g也越大,故f1应为m1g的增函数。m1g中既包含了一级航天器的推进系统m1tg,又包含了结构、热控等其余部分m1tg_else。后续仿真中用数值拟合方法对f1进行近似。
一级推进系统分离后,为完成Δv2的速度增量,二级推进系统所需的燃料质量

式中:Isp2为二级推进系统比冲。
二级航天器的干重可表示为

用函数f2表示二级航天器推进系统的干重,则

用函数g1表示一、二级航天器间分离装置所需质量,即

为评价分离点设计的优劣,本文用有效入轨质量mz作为评价标准。mz的物理意义是可用于二级航天器平台(除推进系统外)与载荷设计的质(重)量资源,有

将式(3)~(5)、(7)~(8)代入式(9),mz即可表示为Δv1的函数。
明显地,在以mz为优化目标的前提下,求mz的极大值即可得最优分离点,对应的Δv1即为一级航天器所需提供的速度增量。相对以往航天器分离界面选取方式,本文将mz作为单一的评价指标,以mz最大化为目的,给出了一种相对明确的分离点定量评价方法,可作为分离式航天器设计的依据。
2 仿真分析
以火星探测任务为背景,用上述数学模型对最优分离点进行仿真分析。取仿真参数为:m0为5 000kg,Δv为2 000~5 000km/s,Isp1为312s,Isp2为220~312s,燃料余量为燃料总量的5%,mf分别为发射总重的0%,0.5%,1%。由工程经验,对m1g与所能提供Δv1的函数关系进行二次多项式拟合,可得

其中,m1tg_else一般不为0。对二级航天器或一体式航天器来说,因m1tg_else被纳入了有效mz,故取值为0。
2.1 理想状态
理想状态下,一、二级推进系统的比冲相同,均为312s,一级航天器的m1tg_else趋于0,mf趋于0。速度增量dv分别为2 000,3 000,4 000,5 000m/s时的最优分离点如图1所示。
由图1可知:在理想状态下,最优分离点出现在总速度增量的约65%处,且任务总速度增量需求越大,分离式航天器相对一体式航天器的优势就越明显。
2.2 推进系统比冲
dv=3 000m/s,二级推进系统比冲Isp2分别为312,300,285,220s时的最优分离点如图2所示。
由图2可知:当二级推进系统比冲降低后,最佳分离点后移,分离式航天器的优势将减小。

图1 理想情况最优分离点Fig.1 Optimal separation point in ideal situation
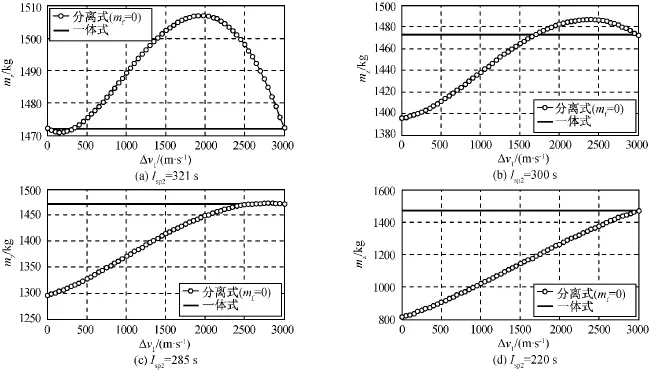
图2 二级推进系统比冲对最优分离点影响Fig.2 Effects of the second stage propulsion specific impulse to optimal separation point
2.3 可分离干重
dv=3 000m/s,m1tg_else分 别 为 10,50,100,150kg时的最优分离点如图3所示。
由图3可知:随着一级航天器m1tg_else的增加,最佳分离点前移,分离式航天器的优势将减小。
2.4 分离装置质量
因各级航天器间的mf可近似为常数,故其对最优分离点的影响较小,不同mf的最优分离点如图4所示。

图3 一级航天器m1tg_else对最优分离点的影响Fig.3 Effects of the first stage separable dry mass to optimal separation point

图4 mf对最优分离点的影响Fig.4 Effects of mfto optimal separation point
由图4可知:随着mf仅对曲线起到平移作用,对最优分离点无影响。考虑mf的影响后,总速度增量增至4km/s以上时,分离式设计优势才体现。
3 算例
当Δv为3km/s时,一体式航天器较分离式更具优势,可多获得更大的有效入轨质量。分离式航天器的最优分离点出现在Δv约1.5km/s处。分离式与一体式航天器的质量分配见表1。可见在该条件下,即使在最优分离点处,分离式航天器的有效入轨质量仍较一体式减少约100kg。
当Δv增至5km/s时,分离式航天器将在最优分离点处获得优势。最优分离点出现在Δv约2.6km/s处。
分离式与一体式航天器的质量分配见表2。可见在该条件下,采用最优分离方案后分离式航天器的有效入轨质量较一体式增加34kg。

表1 算例1(Δv=3km/s)Tab.1 Example 1(Δv=3km/s)

表2 算例2(Δv=5km/s)Tab.2 Example 2(Δv=5km/s)
4 结束语
本文通过对两级推进系统干质量与速度增量的关系进行数学建模,以入轨有效质量为评价标准,提出了一种面向工程应用的分离式深空探测器最优分离点评价方法。理想状态下,分离式航天器较一体式航天具有更大的有效入轨质量,其最优分离点在总速度增量的65%处。但在实际工程应用过程中,推进系统比冲、可分离干重的变化均可能导致最优分离点的移动,分离式设计的优势也可能被引入的额外资源开销抵消。一般而言,任务速度增量需求越大,分离式设计的优势也越明显。在实际设计过程中可通过减小一级干重、增加二级推进比冲和减小分离装置质量的方式以使分离式设计的优势更为明显。
[1] 张 伟,方宝东,成 玫,等.空间飞行器分离式构型设计[J].上海航天,2013,30(1):1-7.
[2] SELLERS J,ASTORE W,GIFFEN R,等.理解航天[M].张海云,李俊峰(译).清华大学出版社,2007.
