一种基于遗传算法的进路搜索算法
2015-12-30张文泉余立建
张文泉 余立建
在铁路车站作业中,进路选排对接发车作业的效率和车站通过能力有着直接影响,如何高速有效地选排接发列车和调车作业进路,是保证行车安全和提高行车效率的重要内容。
在计算机联锁的进路选排中,进路搜索的方法有很多种。最常见的有链表法、二叉树搜索法等。近年来智能优化算法在求解路径优化等问题方面显示了较强的优势,所以也可以采用智能算法来进行进路搜索。本文就提出了一种基于遗 传 算 法 (genetic algorithm,简称GA)的进路搜索算法,这种方法以遗传算法为核心,具有快速、准确的特点,能够有效地进行进路搜索。
1 站场数据结构分析
为了简化建模过程,本文只考虑列车进路选排,暂不考虑调车进路选排,下面以 《6502电气集中电路》中的一个典型站场简化图为例进行分析和建模。如图1所示。
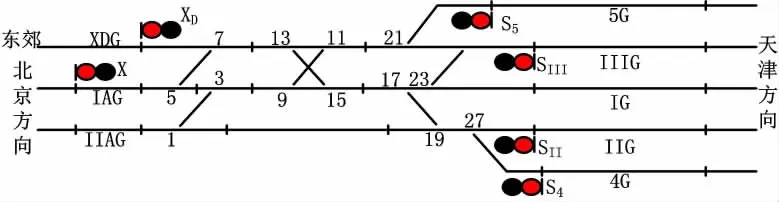
图1 站场平面图
首先需要简化站场图,将站场图以节点的形式进行描述。因进路选排过程中,主要需要考虑信号机、轨道区段和道岔,将信号机、轨道区段以及道岔都作为站场图节点,并进行统一定义。对于图1所示站场,按照由下向上、由左向右的顺序对节点依次进行奇数编号。由于信号机、道岔以及轨道区段在位置上可能重复,所以为了避免重复定义节点,在定义过程中先选择道岔作为节点,再选择轨道区段,最后再考虑信号机。对于一条进路,各个节点的前后连接关系十分重要,所以采用数据结构图表示整个站场,图1站场的数据结构图如图2所示。
图2中,k1,k3…均表示当前节点的编号;pf1表示水平方向上所连接的前一节点的编号,pf2表示渡线方向上所连接的前一节点的编号,若不存在则赋值为0。
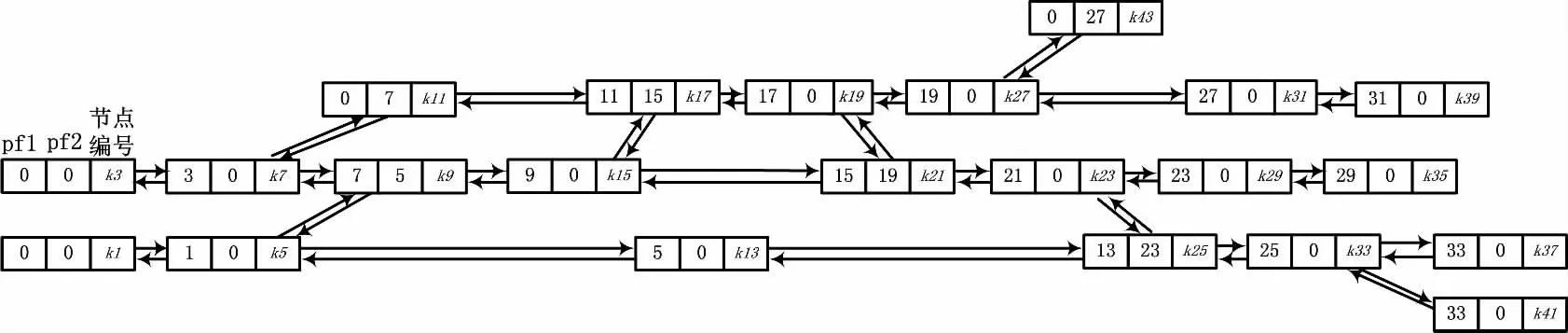
图2 数据结构图
2 进路搜索的遗传算法建模
2.1 编码与染色体
根据节点取值特点,选取二进制编码。在遗传算法中,一条特定的进路可以表示成一条染色体,将一组染色体放入到问题环境中,通过适者生存的规则选择出适合环境的个体进行遗传。Ki表示一条特定的进路,即是一条染色体,Ki= {ki1,ki2,…kin}。
当站场数据结构图确定后,节点数也就随之确定。在进路选排过程中,如果让节点ki为1表示选中、为0表示未选中,则 {k1,k2,…kn}就可以表示一条搜索出的进路。于是进路搜索的问题就可以抽象成在众多的解Ki={ki1,ki2,…kin}中选择最优解的问题。
2.2 进路搜索的遗传操作
设K为进路搜索的集合,算法初始状态的进路搜索集合作为初始种群,在大小为m的初始种群中,Ki表示第i个染色体。遗传算法的基本流程见图3。
在整个遗传算法过程中,主要进行三个遗传操作,分别是复制操作 (选择)、交叉操作和变异操作。复制操作是根据每个个体的适应度大小进行优胜劣汰,将适应度更高的遗传到下一代。本文采用轮盘赌的方法,即将所有个体的适应度求和作为分母,每个个体自身的适应度作为分子,按比例进行选择。因此,每个个体被选择的概率为
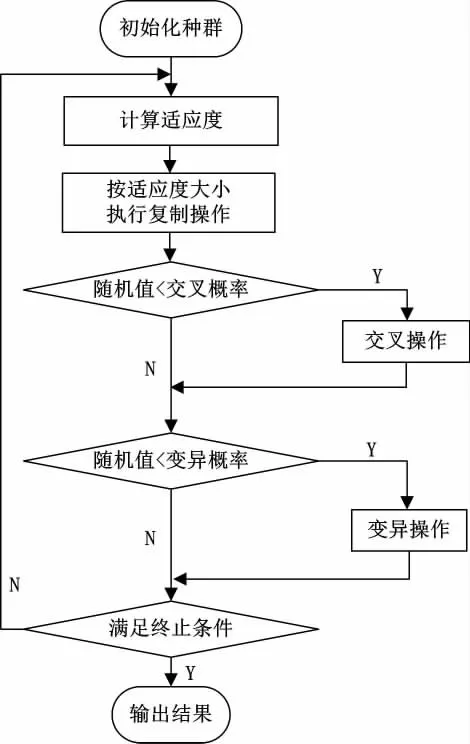
图3 遗传算法流程图

交叉操作是选择父代中2个个体,将这2个个体的某一段进行交换得到新的2个个体,本文采用单点交叉。变异操作是对单个个体进行的操作,在单个个体的某个基因上按照某个较小的概率进行取反操作,使之产生新的个体,从而改善进路搜索能力。
2.3 适应度函数
一个个体若能够构成一条合理的进路,则从始端节点到终端节点需依次相连。即一个个体中去除为0的信息后组成新的子集,该子集所包含的节点应连续。此时,各个节点的节点编号并不发生变化,用一个新的数组n表示。例如,某个个体K为 {0 1 0 1 1 0 0 1 0 0 1 1 0 0 1 0 0 1 0 0 0 0},对应的节点编号为 {1,3,5,…41,43},个体K去除0信息后组成新的子集 K′ 为 {1 1 1 1 1 1 1 1},对应的节点编号为 {3,7,9,15,21,23,29,35},记作数组n。
另外,同一组始端和终端节点之间可能存在着多条进路,因此还需要处理多余的变更进路。根据如上分析,确定了优化目标为

其中,fni表示节点kni的pf1值,f′ni表示节点kni的pf2值,ni表示个体去除0信息后组成子集的节点编号;m表示子集长度;kj表示节点取值,j表示节点编号;s表示始端节点编号;e表示终端节点编号。上式中的第一项表示能否构成合理进路,第二项表示去除多余变更进路。
3 进路搜索模型改进
虽然建立了基于遗传算法的进路搜索模型,但是要将这种模型应用到实际的进路选排过程中,还需要考虑信号灯的变化以及道岔的转动。因此,必须对上述的基本模型进行改进。
首先在一个站场中,每一架列车信号灯均对应一个股道区段,以图1站场图为例就有如表1所示的对应关系。
因此,当该股道区段所对应节点为始端节点时,则该股道区段所对应的列车信号机由红灯状态变为绿灯状态,即信号开放。其次,当选定节点时,相应节点所对应的道岔需要进行动作。为了便于道岔动作的判断,对前面的数据结构进行改进,加入一项新的数据L,即节点所在的股道编号,如图4所示。

图4 改进的单节点数据结构
其中,L(k3)=0,即节点k3所在的股道编号为0。在整个站场中,L(i)表示节点ki所在股道的编号。在搜索到一条进路以后,进路中所有节点的前后节点随之确定。此时,若L(i)≠L(i-1)或者L(i)≠L(i+1),则节点ki所对应的道岔需要转动。

表1 股道与信号灯对应关系
4 实例仿真分析
以图1站场为例,可以选择任意一条列车进路进行选排。下面以北京方向下行至5G接车进路的选排为例进行仿真分析。
步骤1:依次按下始端按钮 (XJA)和终端按钮 (S5LA)。此时,对应的进路搜索起始节点和终止节点被确定,分别是k3和k43,参见图2。
步骤2:利用遗传算法搜索列车进路。遗传算法参数分别为,群体规模取80,交叉概率pc取0.6,突变概率pm取0.1。仿真结果如图5所示。
显然,在迭代32次以后适应度F达到最大值且不再变化,此时F=1.0149。得到的最优个体为 {0 1 0 1 0 1 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 1},对应的最优进路节点为k3-k7-k11-k17-k19-k27-k43。经多次试验表明,遗传算法的初始种群均随机产生,收敛速度也随之变化,但均能在一定的迭代次数后收敛。
步骤3:相应道岔的转动。根据数据结构可知,搜索到的节点确定以后,相对应道岔关系也随之确定,如表2所示。
步骤4:开放信号灯。信号灯的开放和始端按钮 (或起始节点)所在股道区段相关,由于此时的搜索起始节点k3所对应的股道区段是IAG,由表1可知,需开放信号灯X。
至此,整个进路选排完毕,X信号机开放。
值得注意的是在遗传算法的计算过程中,有时会陷入局部最优从而影响最终结果,为了避免这种情况的发生,可以对遗传算法进行改进。同时也可以采用冗余计算的方法,比较选取最优结果,防止局部最优解的出现。
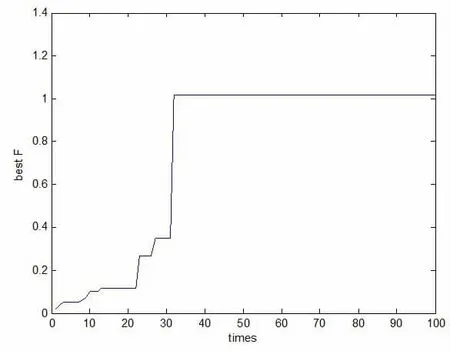
图5 遗传算法仿真结果
5 总结
通过对站场图进行数据结构分析,在此基础上提出了一种基于遗传算法模型的进路选排算法。通过仿真证明,这种进路选排算法可以简单便捷的搜索出一条合理的进路,是一种具有可行性的进路选排算法。

表2 道岔转动关系
[1] 何文卿.6502电气集中电路[M].北京:中国铁道出版社,2011.
[2] 陈志颖,董昱,杨柳,李亮.计算机联锁进路搜索算法的分析与研究[J].铁路通信信号,2007.4,43(4):4.
[3] 陈荣武,刘莉,郭进.基于遗传算法的列车运行能耗优化算法[J].交通运输工程学报,2012.2,12(1):111-112.
