基于遗传算法的直升机旋翼液弹阻尼器模型参数识别

2015-12-30武珅,杨卫东,李锐锐

振动与冲击 2015年10期

第一作者武珅男，博士生，1983年10月生

通信作者杨卫东男，教授，博士生导师，1967年生

武珅1,2，杨卫东2，李锐锐2(1.中国船舶科学研究中心，无锡214082; 2. 南京航空航天大学直升机旋翼动力学重点实验室，南京210016)

摘要：建立直升机旋翼液弹阻尼器非线性动力学参数模型，引入具有全局搜索能力的遗传算法进行模型参数识别，解决因模型复杂造成的传统参数识别效率及精度较低问题。据识别所得参数模型重构力—位移迟滞回线并与液弹阻尼器动力学试验数据对比结果显示，参数模型重构曲线与试验曲线吻合良好，验证参数模型描述液弹阻尼器非线性动力学特性的准确性及采用遗传算法识别模型参数的有效性。对不同位移幅值与不同频率下液弹阻尼器动力学特性模拟计算均获得与试验一致结果，表明非线性参数模型及参数识别方法鲁棒良好性、精度较高。

关键词：直升机；旋翼；液弹阻尼器；遗传算法；参数识别

基金项目：江苏省普通高校研究生科研创新计划资助项目(CX09B_085Z)；江苏高校优势学科建设工程资助项目

收稿日期：2014-04-21修改稿收到日期：2014-06-03

中图分类号:V216.2文献标志码：A

Parametric identification for a fluid-elastomeric damper model of helicopter rotor based on genetic algorithm

WUShen1,2,YANGWei-dong2,LIRui-rui2(1. China Ship Scientific Research Center, Wuxi 214082, China;2. National Key Laboratory of Rotorcraft Aeromechanics, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

Abstract:A nonlinear dynamic parametric model for a fluid-elastomeric damper of helicopter rotor was established. Genetic algorithm having a global search capability was introduced to identify the model parameters. It could solve the problem of lower efficiency and precision of conventional methods in parametric identification for complex models. The force-displacement hysteresis loops reconstructed with the identified parametric model were compared with those derived from test data. Both of them agreed well each other. The results showed that the identified nonlinear parametric model can validly describe the dynamic properties of a fluid-elastomeric damper and the genetic algorithm can effectively identify parameters of the nonlinear fluid-elastomeric damper model; under different displacement amplitudes and frequencies, the dynamic characteristic calculation results of the fluid-elastomeric damper always agree well with test data, so the proposed nonlinear parametric model and the parametric identification method both possess a good robustness and a higher precision.

Key words:helicopter; rotor; fluid-elastomeric damper; genetic algorithm; parametric identification

液弹阻尼器为新型直升机旋翼摆振阻尼器，其在粘弹阻尼器基础上附加液压减振机构，利用橡胶材料剪切变形及粘性液体流动提供弹性刚度及阻尼，抑制直升机旋翼/机体耦合系统振动不稳定现象发生。对液弹阻尼器动力学特性研究结果表明，液弹阻尼器虽具有稳定的动力学性能、良好的减振效果，但也具有非线性的迟滞特性[1-4]。使液弹阻尼器动力学模型描述十分复杂，通常用一组包参数的非线性函数表示，并需结合液弹阻尼器动力学试验数据进行参数辨识最终确定数学模型。以往模型参数识别多采用最小二乘法、梯度法等优化逼近方法[5-6]，但对多目标函数最优解搜寻能力有限且初值选取受人为影响较大，故识别精度和效率较低。如何用具有全局搜索功能、较高识别精度方法进行液弹阻尼器非线性动力学模型参数识别成为急需解决的问题。

遗传算法为模拟自然界生物遗传、变异、进化过程的搜索全局最优解方法，已广泛用于线性规划、图像识别、参数辨识等领域[7-9]。已有利用遗传算法识别结构参数，如李守巨等[10-11]用遗传算法识别材料的热传导参数、动力系统阻尼参数。而针对阻尼器，遗传算法已成功用于磁流变阻尼器Bouc-Wen模型的参数识别[12-14]，并取得良好效果。

基于此，本文结合液弹阻尼器的动力学试验数据，将遗传算法思想用于液弹阻尼器非线性动力学模型参数识别，提出基于遗传算法的液弹阻尼器模型参数识别方法。并据识别所得参数模型重构液弹阻尼器动力学特性曲线，并与试验曲线对比，验证遗传算法识别模型参数的准确可行性及液弹阻尼器非线性动力学模型的可靠性。

1液弹阻尼器动力学试验

图1　液弹阻尼器试验装置图 Fig.1 Experimental set of fluid-elastomeric damper

液弹阻尼器试验装置见图1。液弹阻尼器试件通过液压钳安装在MTS力学性能试验机上，控制台采用正弦加载，力、位移传感器安装于激振杆，分别测量液弹阻尼器在不同位移幅值(1 mm、1.5 mm、2.0 mm)、不同激振频率(1～6 Hz)的力、位移信号，进而得到不同运动状态下反映液弹阻尼器动力学特性的阻尼力—位移迟滞回线，获得液弹阻尼器动力学性能随结构、运动等参数变化规律，为液弹阻尼器动力学模型的准确建立提供数据支持。

液弹阻尼器在2 Hz激振频率不同位移幅值及1.5 mm位移幅值不同频率下阻尼力—位移迟滞回线见图2、图3。

图2　2 Hz频率不同位移幅值下的阻尼力-位移迟滞回线 Fig.2 Damperforce-displacement hysteresis loops at 2 Hz under different amplitude

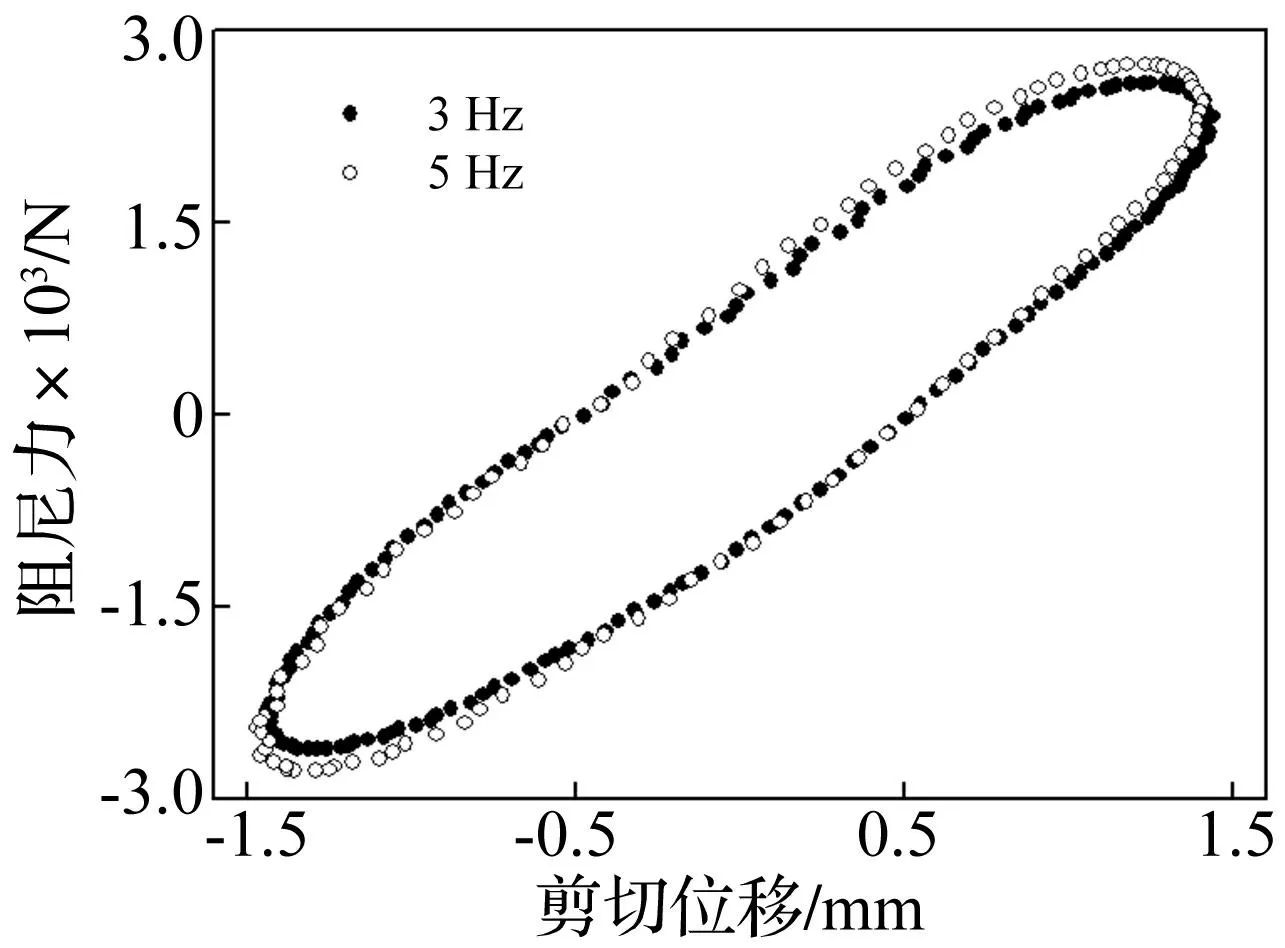
图3　1.5 mm位移幅值不同频率下的阻尼力-位移迟滞回线 Fig.3 Damperforce-displacement hysteresis loops at 1.5 mm amplitude under different frequency

阻尼力—位移迟滞回线所围面积表示结构振动时阻尼器耗散能量大小，长轴斜率代表阻尼器弹性刚度。由图2看出，同频率不同位移幅值的液弹阻尼器力—位移迟滞回线所围形状近似椭圆，面积随位移幅值增大而增大，表明液弹阻尼器减振能力随激振幅值增大而增强。不同运动状态下椭圆长轴斜率基本不变，表明液弹阻尼器弹性刚度接近常数，体现出液弹阻尼器动力学性能的稳定性。图3中相同位移幅值不同频率下液弹阻尼器力—位移迟滞回线所围形状、面积偏差均不大，5 Hz激振频率下阻尼器弹性刚度较3 Hz略有增加，表明激振频率变化对液弹阻尼器动力学特性影响不明显。

2液弹阻尼器非线性参数模型

液弹阻尼器通过粘弹橡胶材料、粘滞液体共同作用产生刚度、阻尼，其输出刚度、阻尼的动力学特性受阻尼器结构、运动、材料及环境等多种复杂因素影响，与输入位移之间呈非线性迟滞关系。摆振阻尼器的动力学特性直接影响直升机旋翼系统的气弹稳定性。进行直升机旋翼系统气弹特性分析时，需获得能准确描述阻尼器非线性应力—应变关系的动力学分析模型。直升机旋翼摆振阻尼器多采用基于复模量的频域建模，据能量等效原则计算阻尼器的复模量、阻尼力。利用频域模型获得到液弹阻尼器复模量、阻尼力—位移迟滞回线所围面积与试验结果均吻合良好，但迟滞回线形状与试验曲线有偏差，表明频域模型虽能正确反映液弹阻尼器的耗能减振性能，但对阻尼器受载荷与激振位移间瞬态关系描述不准确[15]。

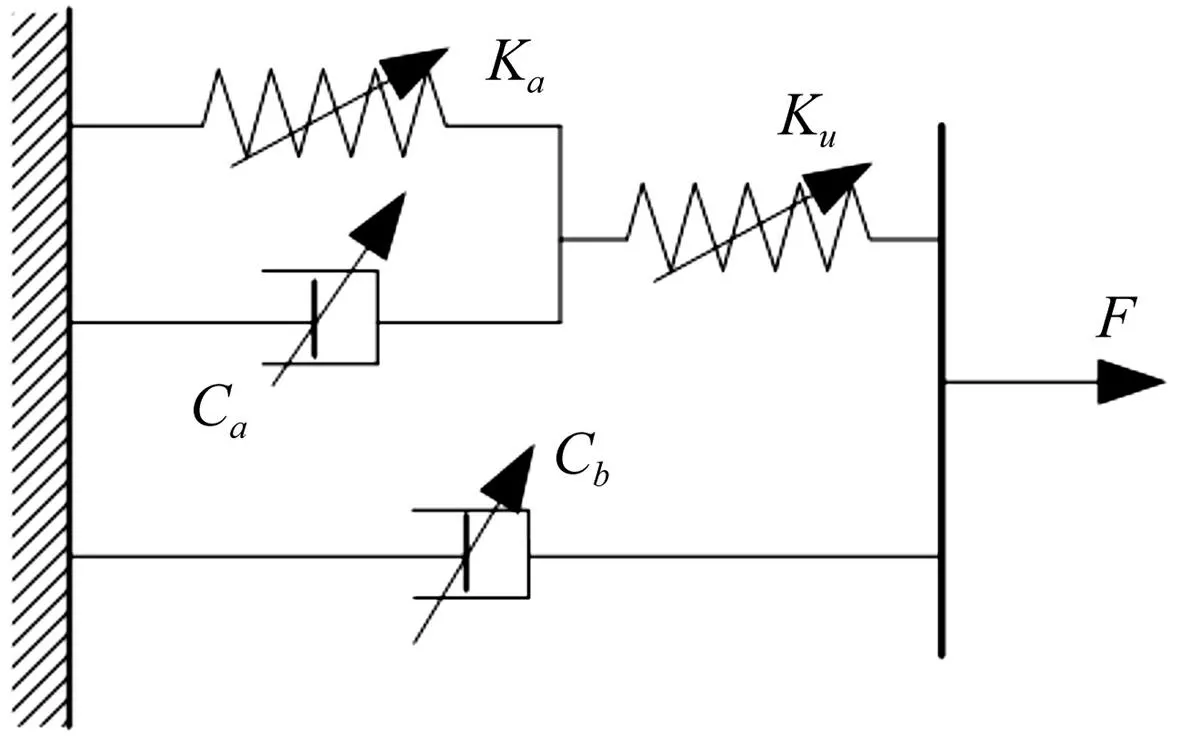
图4　液弹阻尼器模型结构 Fig.4 Fluid-elastomeric damper model structure

据粘弹材料非线性ADF模型及粘性液体伯努利方程建立液弹阻尼器的非线性参数模型，见图4。其中弹簧元件、阻尼元件均为非线性，分别用非线性函数Ku，Ka，Ca，Cb表示。

粘弹材料的本构关系为

(1)

式中：

Ku=ku1+ku2u2+ku3u4+ku4(u-uA)2

(2)

Ka=(ka1-1)Ku

(3)

(4)

(5)

液体运动的等效粘性阻尼为

Cb=kb1x0ω

(6)

液弹阻尼器的外载激励为

x=x0sin(ωt)

(7)

u=x/d

(8)

(9)

式中：x，ω，x0为激振位移、圆频率、位移幅值；d，A分别为橡胶层厚度、横截面积；u，uA，σ，σA分别为粘弹体剪切应变、滞弹应变、应力、滞弹应力；F为总阻尼力；ku1，ku2，ku3，ku4，ka1，kb1，kd1，kd2为非线性弹簧及阻尼元件Ku，Ka，Ca，Cb中所含模型参数， kd1为激振圆频率，模型共7个待识别参数。

以上未知参数无法直接测量，需结合液弹阻尼器动力学试验准确识别，才能得到完整的液弹阻尼器分析模型。识别模型参数目的即寻找模型计算结果与试验结果之间误差最小的解，但对参数较多的复杂模型会产生非线性、多参数、多极值优化问题。经典的梯度优化方法需获得目标函数的导数，但液弹阻尼器参数模型由微分方程组表示，求解时无法获得解析表达式，不易获得目标函数导数；而传统的最小二乘法及梯度搜索会受初值选取影响，无法保证收敛到全局最优解，效率较低。故采用具有全局搜索能力的遗传算法进行液弹阻尼器模型参数识别。

3基于遗传算法的模型参数识别方法

遗传算法为借鉴生物界自然选择、遗传变异等作用机制的全局概率随机搜索算法，根据定义的适应度函数对个体进行评估，模拟自然界“优胜劣汰”原则选择、交叉、变异进而获得最优解。遗传算法参数识别的计算流程见图5。主要步骤如下：

(1)给定种群规模、个体染色体长度等基本参数，设定待识别模型参数上下限范围，随机产生初始种群。

(2)计算种群中个体目标函数及适用度函数。将种群中二进制个体进行十进制转换，得待识别参数值

K=[ku1,ku2,ku3,ku4,kd2,ka1,kb1]

(10)

将各参数值分别代入式(1)～式(9)，选与试验数据取样时间相同的步长，用二阶梯形公式对方程组数值求解，获得各位移数据点模型计算阻尼力大小。因参数识别目标为使数学模型计算结果与试验数据之间误差尽量小，目标函数定义为

(11)

式中：n为数据点个数；Fe(i)，Fm(i)分别为第i个数据点试验、模型仿真阻尼力大小。

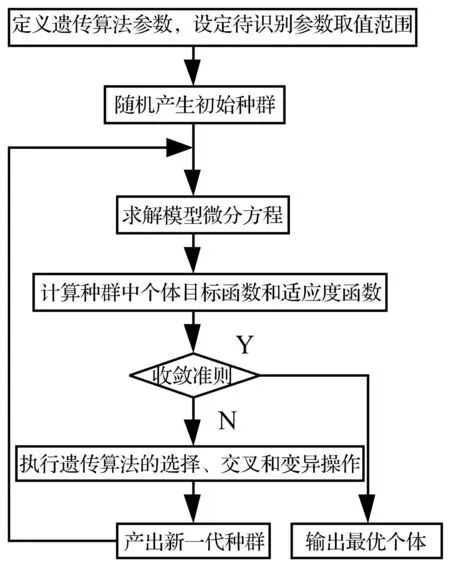
图5　遗传算法参数识别的计算流程图 Fig.5 Flow chart of parameter identification by genetic algorithm

据目标函数大小对种群中个体排序，按排序分配个体适应度。由于定义目标函数大小反映识别参数模型仿真结果与试验数据误差，故目标函数越小个体适用度越大。

(3)设定遗传最大进化代数作为收敛准则，满足则得到适应度最高个体，输出全局最优解；否则执行下一步。

(4)执行遗传算法的选择、交叉、变异操作。遗传算法选择操作有轮盘赌法、随机遍历抽样、锦标赛等。本文采用轮盘赌法，据步骤(2)运算所得基于排序的个体适用度值选择个体，适用度值越大被选择的概率越高。

由于对模型参数进行二进制编码，故在交叉重组过程中采用单点交叉方式。参与交叉的个体在种群中两两配对，随机产生交叉点，再按预定交叉概率互换两个体的部分染色体从而产生新个体。为增加种群的多样性，防止寻优解过程过早收敛，在个体选择、重组后施加的扰动操作称为变异。个体染色体基因通常按较小的预定概率变异从而产生子代个体。经选择、交叉、变异的遗传操作后，产生新一代种群，返回步骤(2)继续优化计算。

4参数识别与模型验证

算例：遗传算法的种群大小P=50，个体染色体长度L=20，交叉率pc=0.7，变异率pm=0.05，最大进化代数M=100。选4 Hz激振频率，不同剪切位移幅值x0=1 mm，1.5 mm，2 mm的试验数据作为式(11)中Fe(i)分别进行模型参数识别。据三组不同试验数据，遗传算法识别的模型各参数值见表1。

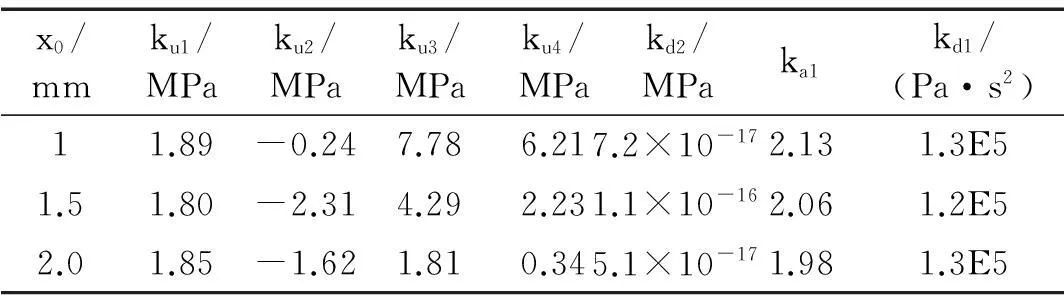
表1　用J作为遗传算法目标函数运算所得各参数值

将表1中各组识别参数分别代入模型重构液弹阻尼器的力—位移迟滞回线，并与试验曲线对比，见图6～图8。图6为以位移幅值1 mm的试验数据，据识别所得参数模型对三种位移幅值状态动力学特性模拟获得三组模型重构曲线(Ⅰ～Ⅲ)。同样，图7、图8则分别以位移幅值1.5 mm，2 mm的试验数据，据识别所得参数模型模拟获得三组曲线与试验曲线对比。由三图看出，每组识别参数在相应状态下的模型仿真曲线与试验曲线均吻合良好，但仿真其它状态曲线与试验数据出现较大误差。如图6中，Ⅰ组仿真曲线与试验曲线吻合较好，但Ⅱ、Ⅲ组曲线则偏差较大。而图7、图8中分别只有Ⅱ组、Ⅲ组曲线非常接近。表明据每组模型参数仿真结果均能准确模拟各自状态的动力学特性，而无法准确描述液弹阻尼器在不同位移幅值的动力学特性。此外，遗传算法识别模型参数时仅以适应度函数作为解搜索依据时，在模型参数识别中需考虑更多幅变特性信息，对原识别方法目标函数进行修正。

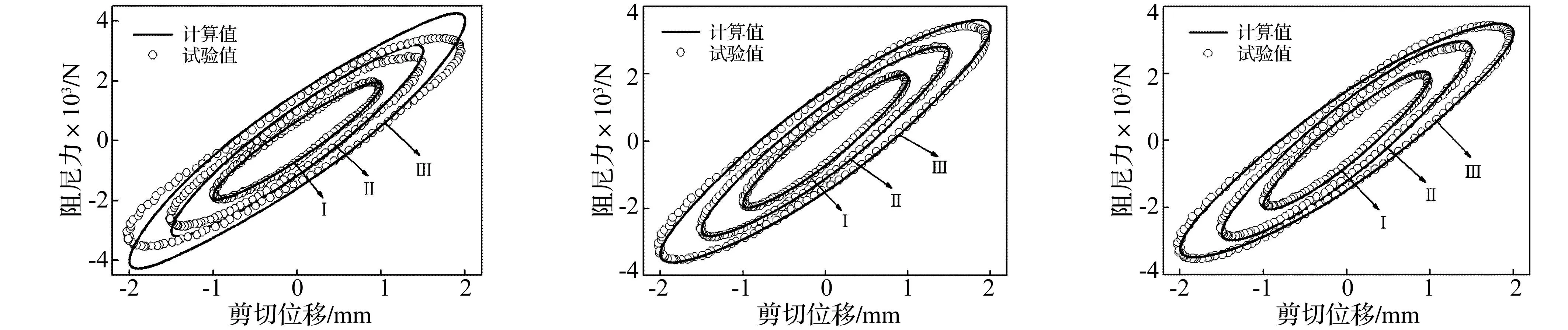
图6 x0=1mm识别的参数模型仿真曲线与试验曲线对比Fig.6Comparisonbetweenexperimentaldataandcurvessimulatedwithparametersidentificationatx0=1mm图7 x0=1.5mm识别的参数模型仿真曲线与试验曲线对比Fig.7Comparisonbetweenexperimentaldataandcurvessimulatedwithparametersidentificationatx0=1.5mm图8 x0=2mm识别的参数模型仿真曲线与试验曲线对比Fig.8Comparisonbetweenexperimentaldataandcurvessimulatedwithparametersidentificationatx0=2mm

将原目标函数J修正为JJ，即

(12)

式中：m为所选运动状态个数。

选遗传算法基本参数及3组试验状态数据，用式(12)作为遗传算法运算的目标函数，所得模型各参数识别结果见表2。

表2　用JJ作为遗传算法目标函数所得各参数值

将表2中识别结果代入分析模型，重构4 Hz激振频率，1 mm，1.5 mm，2 mm位移幅值下的液弹阻尼器力—位移迟滞回线，并与试验曲线对比，见图9。与图6～图8结果不同，图9中三种运动状态下液弹阻尼器力—位移重构迟滞回线均能与试验曲线良好吻合，说明在运用遗传算法识别液弹阻尼器模型参数时，同频率下用单组试验数据识别的参数模型不能全面反映液弹阻尼器动力学特性，但计入多组运动状态动力学试验数据，进行目标函数修正后的识别参数模型能正确反映该频率下液弹阻尼器幅变特性，同时也验证模型参数识别方法的可靠有效。

鉴于液弹阻尼器模型参数在4 Hz激振频率不同位移幅值下的试验数据获得，仍需据识别所得参数模型模拟液弹阻尼器在其它频率、位移幅值状态下的动力学特性，验证液弹阻尼器非线性参数模型的正确性、全面性。据表2中识别模型参数，液弹阻尼器在3 Hz、5 Hz激振频率下，1 mm，1.5 mm，2 mm位移幅值模型重构曲线，并分别与试验曲线对比见图10、图11。由图10、图11看出，以4 Hz激振频率试验数据识别所得参数模型为依据，3 Hz及5 Hz频率下的液弹阻尼器动力学特性模型重构曲线与试验曲线基本吻合。表明用单组频率运动状态试验数据作为目标函数的参数识别结果不仅能正确反映参与参数识别运动状态的液弹阻尼器动力学特性，亦能准确反映其它频率运动状态的动力学变化规律。可见，用遗传算法进行模型参数识别时，只要获得任意频率下不同位移幅值的动力学试验数据，即可据非线性参数模型准确模拟出液弹阻尼器所有运动状态的动力学特性。在一定程度上证明液弹阻尼器具有非线性的幅变特性及相对不明显的频变特性。

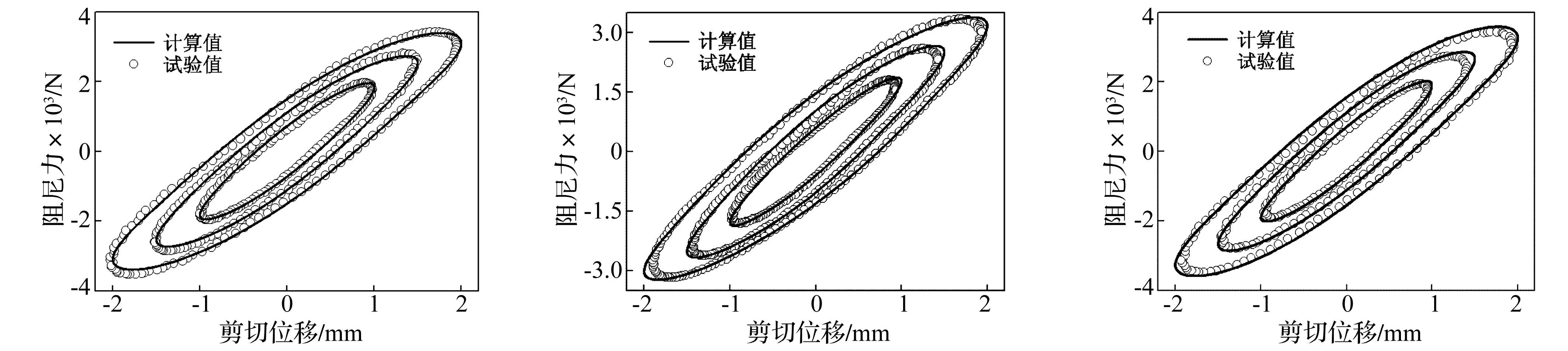
图9 4Hz激振频率下模型仿真曲线与试验曲线对比Fig.9Comparisonbetweensimulatedcurvesandexperimentaldataat4Hz图10 3Hz激振频率下模型仿真曲线与试验曲线对比Fig.10Comparisonbetweensimulatedcurvesandexperimentaldataat3Hz图11 5Hz激振频率下模型仿真曲线与试验曲线对比Fig.11Comparisonbetweensimulatedcurvesandexperimentaldataat5Hz

总之，遗传算法可全面、准确进行液弹阻尼器非线性动力学模型参数识别，且识别结果精度较高；本文液弹阻尼器非线性参数模型不仅能正确模拟参与参数识别的试验数据状态，且对其它频率、位移幅值下液弹阻尼器动力学特性亦能准确描述，从而证明液弹阻尼器非线性动力学模型的有效、可靠。

5结论

(1)遗传算法在无任何先知条件下可仅据试验数据识别液弹阻尼器模型参数，解决其它模型参数识别方法效率、精度较低问题。识别参数模型对不同运动状态下液弹阻尼器动力学特性均能较好模拟，表明基于遗传算法的非线性模型参数识别方法有效、可行，鲁棒性良好、精度较高。

(2)不同频率、不同位移幅值下模型重构力—位移迟滞回线与试验曲线均能较好吻合，说明液弹阻尼器非线性参数模型可靠、有效，能准确模拟液弹阻尼器在不同运动状态下的动力学特性。本文非线性参数模型可作为液弹阻尼器的动力学分析模型，用于带液弹阻尼器的直升机旋翼/阻尼器耦合系统气弹稳定性分析。

参考文献

[1]Panda B, Mychalowycz E, Tarzanin F J．Application of passive dampers to modern helicopters [J]． Smart Mater. and Struct., 1996, 5(5): 509-516.

[2]Hu W, Werel N, Chemouni L. Semi-active linear stoke magnetorheological fluid-elastic damper for helicopter main rotor blades [J]. Journal of Guidance, Control and Dynamics, 2007, 30(2): 565-575.

[3]Ngatu G, Hu W, Werely N M. Adaptive snubber-type magnetorheological fluid-elastomeric helicopter lag damper [J]. AIAA Journal, 2010, 48(3): 598-610.

[4]武珅,杨卫东. 旋翼液弹阻尼器模型试验与非线性动力学特性分析[J]. 南京航空航天大学学报,2011,43(3): 318-323.

WU Shen, YANG Wei-dong. Model experiment on nonlinear dynamics characteristics of rotor fluidlastic damper[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2011, 43(3): 318-323.珅,杨卫东. 旋翼液弹阻尼器模型试验与非线性动力学特性分析[J]. 南京航空航天大学学报,2011,43(3): 318-323.

WU Shen, YANG Wei-dong. Model experiment on nonlinear dynamics characteristics of rotor fluidlastic damper[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2011, 43(3): 318-323.

[5]Yun H B, Tasbighoo F, Masri S F,et al. Comparison of modeling approaches for full-scale nonlinear viscous dampers [J]. Journal of Vibration and Control, 2008, 14(1/2): 51-76.

[6]Lewandowski R, Chorazyczewski B. Identification of the parameters of the kelvin-voigt and the maxwell fractional models, used to modeling of viscoelastic dampers[J]. Computers and Structures, 2010, 88: 1-17.

[7]Mohebbi M, Joghataie A. Design optimal tuned mass dampers for nonlinear frames by distributed genetic algorithm[J]. The Structural Design of Tall and Special Buildings, 2011, 21(2): 77-95.

[8]高军,黄再兴. PBX炸药粘弹性损伤本构模型的参数识别[J]. 工程力学,2013,30(7)：299-304.

GAO Jun, HUANG Zai-xing. Parameter identification for viscoelastic damage constitutive model of PBX[J]. Engineering Mechanics, 2013, 30(7): 299-304.军,黄再兴. PBX炸药粘弹性损伤本构模型的参数识别[J]. 工程力学,2013,30(7)：299-304.

GAO Jun, HUANG Zai-xing. Parameter identification for viscoelastic damage constitutive model of PBX[J]. Engineering Mechanics, 2013, 30(7): 299-304.

[9]周明,孙树栋. 遗传算法原理及应用[M]. 北京: 国防工业出版社, 1999: 18-32.

[10]李守巨,刘迎曦. 改进遗传算法在非线性热传导参数识别中的应用[J]. 工程力学,2005, 22(3):72-75.

LI Shou-ju, LIU Ying-xi. Application of improved genetic algorithm to solving inverse heat conduction problems [J]. Engineering Mechanics, 2005, 22(3): 72-75.

[11]李守巨,刘迎曦,冯颖. 基于混合遗传算法的动力系统阻尼参数识别方法[J]. 计算力学学报,2004, 21(5):551-556.

LI Shou-ju, LIU Ying-xi, FENG Ying. Identification of the damping coefficients in dynamic system using hybrid genetic algorithm [J]. Chinese Journal of Computational Mechanics, 2004, 21(5):551-556.守巨,刘迎曦,冯颖. 基于混合遗传算法的动力系统阻尼参数识别方法[J]. 计算力学学报,2004, 21(5):551-556.

LI Shou-ju, LIU Ying-xi, FENG Ying. Identification of the damping coefficients in dynamic system using hybrid genetic algorithm [J]. Chinese Journal of Computational Mechanics, 2004, 21(5):551-556.

[12]Sireteanu T, Giucla M, Mitu A M. Identification of an extended bouc-wen model with application to seismic protection through hysteretic devices[J]. Comput Mech, 2010, 45: 431-441.

[13]关新春,郭鹏飞,欧进萍. 磁流阻尼器的多目标优化设计与分析[J]. 工程力学,2009,26(9)：30-35.

GUAN Xin-chun, GUO Peng-fei, OU Jin-ping. Multi-objective optimization of magnetorheological fluid dampers [J]. Engineering Mechanics, 2009, 26(9): 30-35.

[14]刘永强,杨绍普,廖英英,等. 基于遗传算法的磁流变阻尼器Bouc-Wen模型参数辨识[J]. 振动与冲击,2011,30(7)：261-265.

LIU Yong-qiang, YANG Shao-pu, LIAO Ying-ying et al. Parameter identification of bouc-wen model for MR damper based on genetic algorithm[J]. Journal of Vibration and Shock, 2011, 30(7): 261-265.

[15]吴晓莉. 粘弹减摆器参数影响分析与试验研究[D]. 南京：南京航空航天大学，2009. B, Mychalowycz E, Tarzanin F J．Application of passive dampers to modern helicopters [J]． Smart Mater. and Struct., 1996, 5(5): 509-516.