多点激励功率谱再现振动试验控制研究

第一作者王海东男，高级工程师，1975年6月生

多点激励功率谱再现振动试验控制研究

王海东1，栾强利2，陈章位2，贺惠农3(1.上海航天精密机械研究所，上海200233；2.浙江大学流体动力与机电系统国家重点实验室，杭州310027；3.杭州亿恒科技有限公司，杭州310015)

摘要：通过对多点激励功率谱再现振动试验控制算法研究.设计基于偏相干分析理论的振动试验系统频响矩阵辨识策略，针对系统频响矩阵存在奇异点及系统频响矩阵为长方矩阵情形，设计基于求解频响矩阵广义逆和矩阵最小范数最小二乘解的Moore-Penrose逆系统解耦算法。针对传统差分修正驱动谱控制算法中存在系统功率谱自谱为负数或零值问题，通过引进比例均方根反馈修正算法，设计改进的功率谱均衡控制策略，有效避免功率谱均衡过程中自谱产生负值或零值问题。多点激励功率谱再现振动试验表明，改进的功率谱均衡控制策略对多点激励系统具有可靠、高精度的控制效果。

关键词：偏相干分析；系统解耦；比例均方根反馈修正；功率谱均衡

收稿日期：2014-01-02修改稿收到日期：2014-04-29

中图分类号:O324; TB535文献标志码：A

Control designs for multi-exciter power spectral density replication vibration tests

WANGHai-dong1,LUANQiang-li2,CHENZhang-wei2,HEHui-nong3(1. Shanghai Spaceflight Precision Machinery Institute，Shanghai 200233，China;2.The State Key Lab of Fluid Power Transmission and Control, Zhejiang University, Hangzhou 310027, China;3.Hangzhou ECON Science and Technology Co., LTD, Hangzhou 310015, China)

Abstract:Through studying the control algorithm for multi-exciter PSD (power spectral density) replication vibration tests, an identification strategy for the frequency response matrix of a vibration test system based on partial coherence analysis was designed. For situations of singular points existing in a system frequency response matrix and the matrix being rectangular, different system decoupling algorithms were desgined based on the solutions to the matrix generalized inverse and its Moore-Penrose inverse with the minimum norm and least square methods. Aiming at the situation that the system APSD (auto-power spectral density) might be negative or zero in the traditional difference correction of the drive spectral control algorithm, an improved PSD equalization control strategy was designed by introducing a proportional RMS feedback correction algorithm. The algorithm could effectively avoid the APSD being negative and zero in the process of PSD equalization. The multi-exciter PSD replication vibration tests showed that the improved PSD equalization control strategy can achieve a reliable, high-precision control effect on a multi-exciter vibration system.

Key words:partial coherence analysis; system decoupling; proportional RMS feedback correction; PSD equalization

振动试验通过模拟产品工作过程中可能承受的各种振动环境，可有效评估产品设计可靠性。由于对产品工作可靠性要求越来越苛刻，尤其航空航天领域，各类元器件、组合件及整机均需进行振动试验，可及时暴露系统中各环节可能存在的缺陷及不足。以便快速整改及优化，从而保证满足产品工作可靠性[1-3]要求。功率谱再现试验广泛用于各类产品的振动试验，通过在振动台上复现规定参考谱，检验产品及关键零部件可靠性。

振动试验据激励点不同分为单、多点激励。其中多点激励能提供更大推力，充分考虑产品不同部位振动响应，尤其适用于航空航天类产品复杂化、大型化、重型化结构特点。多点激励振动试验[4-7]对多点激励振动控制相关理论发展、完善具有开创性贡献。Underwood等[8-10]则在多点激励正弦试验自适应控制、频响函数矩阵奇异点控制及多输入多输出(Multiple-Input Multiple-Output)振动控制方面进行深入研究。国内研究已取得诸多理论及实践突破[11-15]。本文在已有成果基础上，利用偏相干分析理论进行多点激励振动试验系统辨识，并在功率谱均衡过程中通过采用改进比例均方根修正算法实现驱动信号更新；通过双点同向激励振动试验对控制算法进行验证。试验表明，控制算法对振动试验系统控制效果较好。

1传递函数辨识

传递函数是整个振动试验系统的特性描述，因此其参数辨识的好坏对整个试验系统控制效果有重要影响。传递函数偏相干分析理论通过将信号中与其它信号相干部分去掉，计算剩余信号对输出信号影响[16-18]。多点激励问题可表示为多个简单多输入单输出(MISO)问题。简单多输入单输出系统见图1。

图1　原始多输入单输出系统 Fig.1 The original multiple-input single-output (MISO) system

该系统表达式为

(1)

式中：Xi为第i{i=1,2…q}个输入信号频谱；Y为输出信号频谱；Hiy为输入Xi到输出Y的频响函数；N为系统中存在的噪声干扰。

将条件输入信号代替图1中原始输入信号，所得条件多输入单输出系统见图2，其为原始多输入单输出系统的等效模型。

图2　条件多输入单输出系统 Fig.2 The conditional multiple-input single-output (MISO) system

该系统表达式为

(2)

式中：Xi(i-1)!为原始输入信号Xi去除X1…Xi-1线性影响后残差，且两两互不相关；Liy为等效模型频响函数，不同于原始频响Hiy。

定义条件系统(图2)产生最小系统均方误差的传递函数为

(3)

式中：Siy(i-1)!为Xi(i-1)!与Y的互谱；Sii(i-1)!为Xi(i-1)!的自谱。

将Y用Xj代替，得

(4)

由式(1)、(3)、(4)，并经推导得

(5)

式(5)为原始多输入单输出系统与条件多输入单输出系统之关系。原始系统频响可由条件输入系统频响求得，Lij为对角线为1的上三角矩阵。将多输入单输出系统频响估计方法用于多输入多输出系统，可实现对MIMO系统频响估计，M输入N输出系统的频响估计流程见图3。

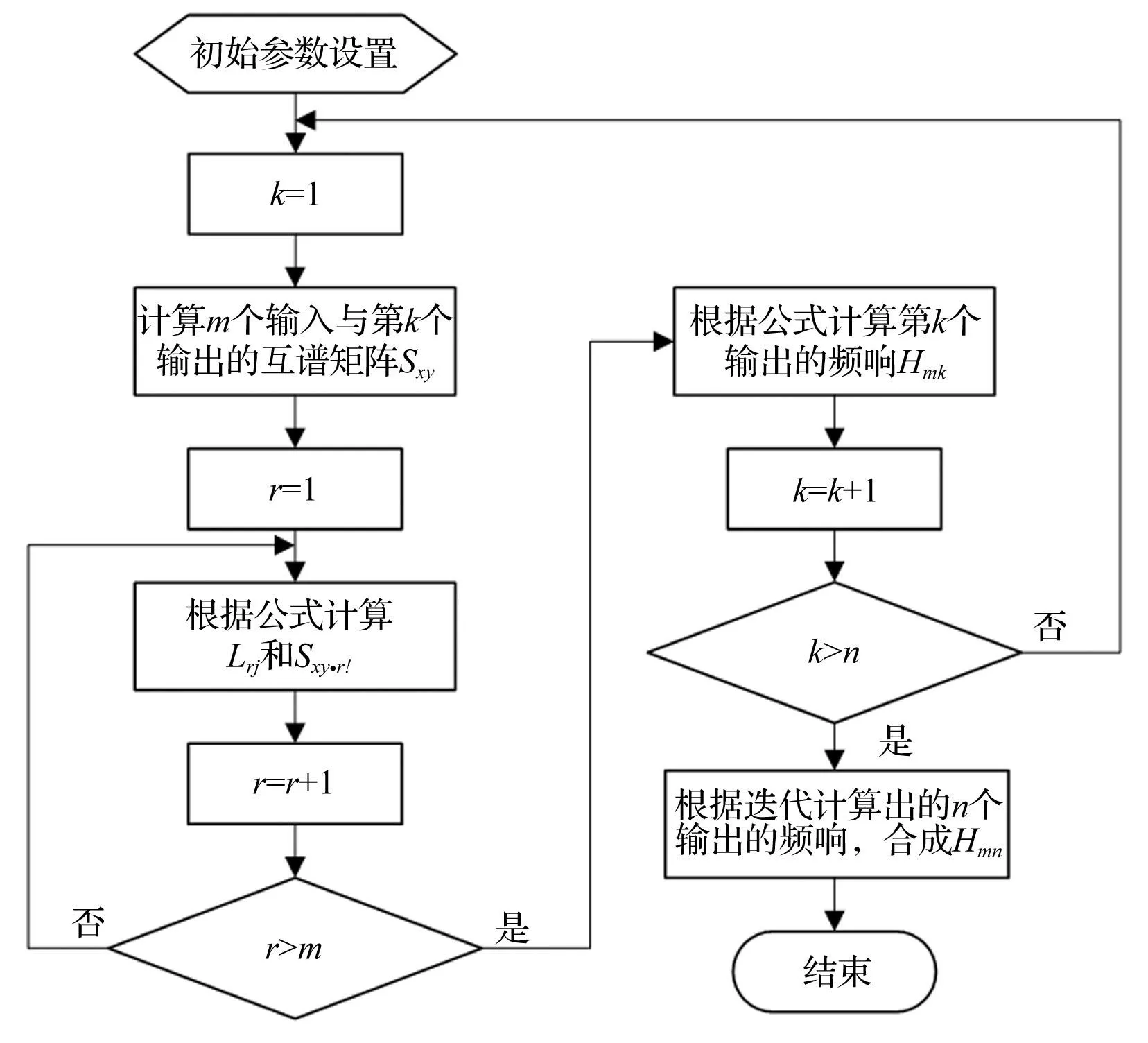
图3　多输入多输出系统频响估计流程 Fig.3 The flow chart for the estimation of system frequency response matrix of a multiple-input multiple-output (MIMO) system

2系统解耦

多点激励功率谱再现过程中需求得系统频响矩阵的逆，即需对系统进行解耦。当系统频响矩阵为方阵(激励点数等于响应点数)且非奇异时，系统解耦补偿矩阵唯一确定，即系统频响矩阵的逆。

系统频响矩阵为方阵时，振动试验过程中系统结构共振点处频响矩阵易发生奇异，导致较大控制误差，因此可采用奇异值分解方法求解奇异矩阵的广义逆。当系统频响矩阵为长方矩阵(激励点数不等于响应点数)时，需求解长方矩阵具有最小范数最小二乘解的Moore-Penrose逆。对分块长方矩阵L=(A,B)，则长方矩阵最小范数最小二乘解的Moore-Penrose逆为

L*=[A(I,A*B)]*=(I∶A*B)*A*=

(6)

3控制方法

3.1驱动信号生成

多点激励振动试验系统中驱动信号与控制信号频谱可表示为

D(f)=[H(f)]-1C(f)

(7)

式中：D(f)，C(f)分别为驱动信号、控制信号频谱；H(f)为系统频响矩阵。

多点激励功率谱再现振动试验中[GRR]，[GDD]，[GCC]分别表示参考信号、驱动信号及控制信号功率谱密度，多点激励功率谱再现目的为使系统控制信号功率谱[GCC]等于系统参考信号功率谱[GRR]。由式(7)得

[GDD]=[Z][GRR][Z]H

(8)

式中：[Z]=[H]-1为系统解耦补偿矩阵；[GRR]为参考谱矩阵，可用n个独立白噪声向量{W}及1个下三角矩阵[L]表示，同时对驱动谱矩阵[GDD]作Cholesky分解，得

[GDD]=[D][D]H

(9)

DDH=[Z][L]{W}{W}H[L]H[Z]H

(10)

由此获得系统驱动信号频谱，即

D=[Z][L]{W}

(11)

3.2迭代修正算法

为实现多点激励振动试验系统高精度功率谱再现，需对试验系统采用闭环控制策略。由于传统的差分修正驱动谱控制算法据控制点位置不同赋予不同优先权，导致系统参考谱中位置靠前的自谱控制效果较好，而位置靠后的自谱控制效果较差，甚至导致自谱负数。为此，本文采用比例均方根反馈修正算法[19]，即

[L]i+1=[L]i[Δ]i

(12)

(13)

(14)

式中：i为迭代次数。

当参考谱与响应谱存在误差时，采用比例均方根修正算法对下三角矩阵[L]进行修正，可避免功率谱对角元素出现负值或零值；但比例均方根修正算法主要针对功率谱对角元素修正，并不单独考虑非对角元素，互谱控制在修正自谱中自行完成，将导致互谱控制无法实现准确、高精度控制。因此，采用振动系统频响矩阵实时修正算法，实现功率谱矩阵的自谱、互谱控制。改进的功率谱再现控制流程见图4。为避免由于控制谱相干系数过高导致功率谱矩阵奇异，当目标控制谱相干系数小于0.95时，可采用频响矩阵修正方法；当相干系数大于0.95时采用修正参考谱矩阵下三角矩阵[L]方式实现驱动信号修正。本文综合考虑两种控制修正方法，设计出改进功率谱均衡控制策略，以逆补各自不足，实现多点激励功率谱再现振动控制的高精度。

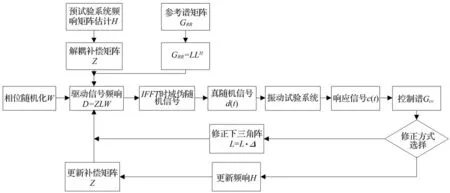
图4　改进的功率谱再现控制框图 Fig.4 The control block diagram of the improved PSD replication

4振动试验

为进一步验证控制算法对多点激励功率谱再现振动试验的控制效果，建立振动试验系统见图5。系统中选基于控制算法的ECON多点激励振动控制器，并采用双点激励、响应控制。振动台及加速度传感器参数见表1。

图5　双输入双输出振动试验系统 Fig.5 A double-input double-output vibration test system

功率谱再现振动试验中，信号频率范围20～2 000 Hz，自谱相同，互谱相位差为0°，相干系数设为1。系统的解耦补偿(阻抗)曲线见图6。由图6看出，系统在160 Hz、602 Hz、1 245 Hz附近有奇异点。系统自谱、互谱控制曲线分别见图7、图8。由图7、图8可知，在系统具有明显反共振点情况下(图6)，控制算法控制效果较好，自功率谱幅值控制在±1.5 dB范围，互功率谱相干函数及相位波动控制在有限波动范围，保证系统自功率谱的高精度再现。

表1　振动试验系统参数

图6　振动试验系统阻抗曲线 Fig.6 The impedance curves of the vibration test system

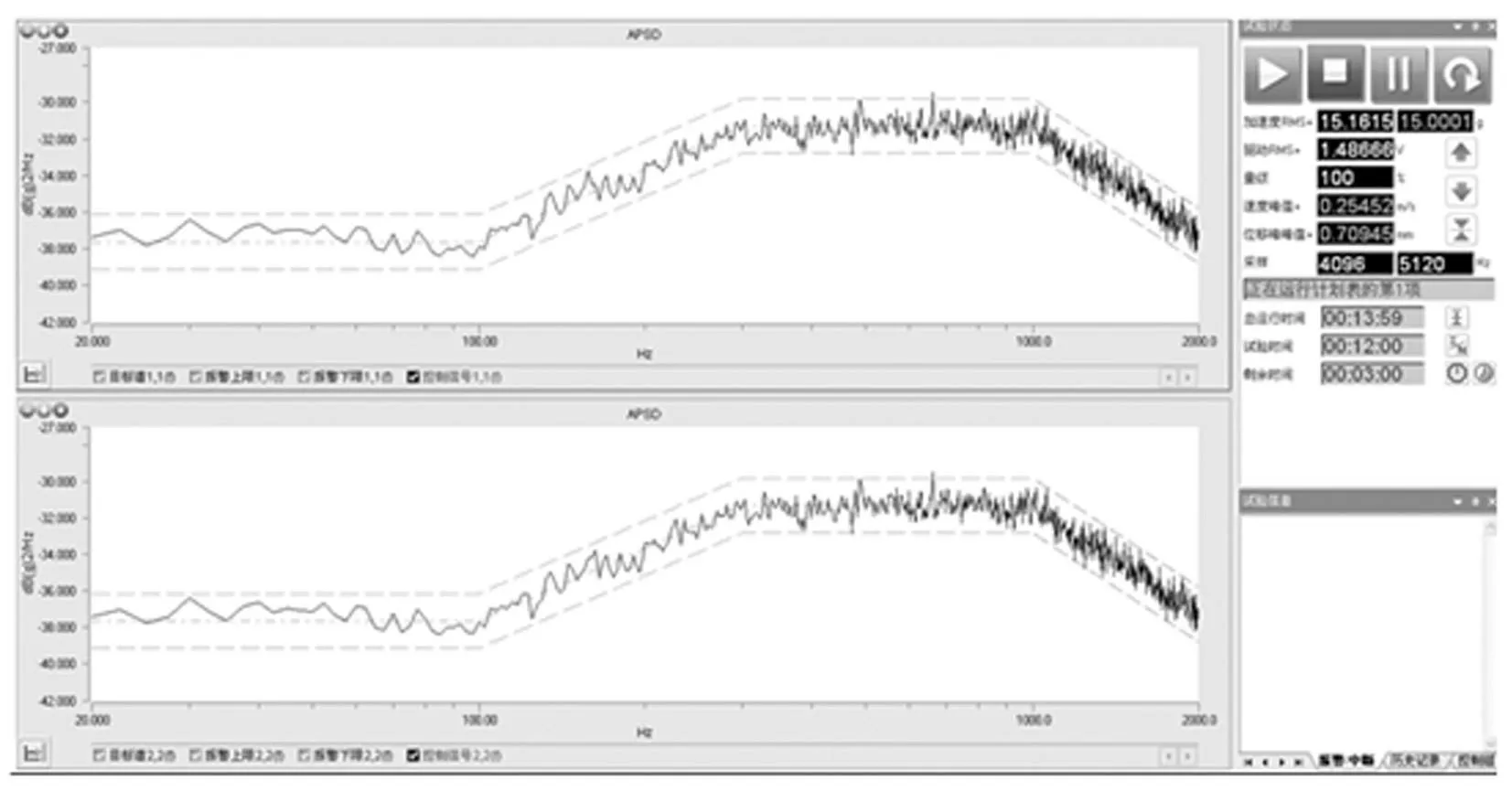
图7　振动试验系统自谱控制曲线 Fig.7 The APSD control curves of the vibration test system

图8　振动试验系统互谱控制曲线 Fig.8 The CPSD control curves of the vibration test system

5结论

(1)通过对多点激励功率谱再现振动试验相关理论、算法深入研究，设计出基于偏相干理论的系统频响矩阵估计方法；针对系统频响矩阵中奇异现象及系统长方矩阵存在，设计出相关的解耦控制算法；针对传统频谱均衡修正算法中存在可能导致系统功率谱自谱为负数或零值问题，设计出改进的功率谱均衡控制策略。

(2)通过对双点激励、控制振动试验系统进行随机振动试验表明，振动系统存在奇异点时，通过控制策略可实现振动系统可靠、准确的功率谱再现。

参考文献

[1]王述成. 振动试验实时控制系统的研究[D]. 杭州：浙江大学，2006.

[2]齐晓军. 航天器振动试验控制技术研究[D]. 长沙：国防科学技术大学，2011.

[3]王珂晟,雷勇军,朱晓莹. 系统级产品振动试验的探讨与研究[J]. 振动与冲击, 2004, 23(4): 112-115.

WANG Ke-sheng, LEI Yong-jun, ZHU Xiao-ying. Investigation on vibration testing for system_level equipments[J]. Journal of Vibration and Shock,2004, 23(4):112-115.

[4]Smallwood D O. Multiple shaker random control with cross coupling [A]. Proceedings of the IES[C].1978: 341-347.

[5]Smallwood D O. Random vibration testing of a single test item with a multiple input control system[A]. Proceedings of the IES[C].1982: 42-49.

[6]Smallwood D O, Woodall T D, Buksa E J. Minimum driver requirements for a multiple input multiple output linear system [A]. Proceedings of the IES[C].1986: 295-301.

[7]Smallwood D O. Multiple shaker random vibration control-an update [A]. Proceedings of the IEST[C].1999:212-221.

[8]Underwood M A, Keller T. Recent system developments for multi-actuator vibration control[J]. Sound and Vibration, 2001, 35(10):16-23.

[9]Underwood M A. Adaptive control method for multiexciter sine tests[P]. United States Patient:5299459, 1994-04-05.

[10]Underwood M A,Keller T. Apparatus and method for adaptive closed loop control of shock testing system[P]. United States Patent, 5517426, 1996-05-14.

[11]陈家焱. 多点激励振动试验系统的控制策略研究[D]. 杭州：浙江大学,2011.

[12]贺旭东,陈怀海. 多点随机振动控制中的互谱矩阵研究[J].南京航空航天大学学报,2004, 36(6): 744-747.

HE Xu-dong, CHEN Huai-hai. Cross-spectra in multiple shaker random vibration test [J]. Journal of Nanjing University of Aeronautics & Astronautics,2004,36(6):744-747.

[13]贺旭东,陈怀海. 一种多点随机振动试验控制的新方法研究[J]. 振动工程学报,2004, 17(1): 49-52.

HE Xu-dong, CHEN Huai-hai. A new method for the control of multi-shakers in random vibration tests[J]. Journal of Vibration Engineering, 2004, 17(1): 49-52.

[14]叶建华,李传日. 多点随机振动试验控制技术[J]. 系统工程与电子技术,2008, 30(1):124-127.

YE Jian-hua, LI Chuan-ri. Systems engineering and electronics[J]. Journal of Systems Engineering and Electronics, 2008, 30(1):124-127.

[15]陈家焱,王海东,周建川,等. 多点激励振动试验控制技术进展[J]. 振动与冲击,2011, 30(3): 69-73.

CHEN Jia-yan, WANG Hai-dong, ZHOU Jian-chuan, et al. Progress in multi-exciter vibration testing control technology [J]. Journal of Vibration and Shock, 2011, 30(3): 69-73.

[16]马忠成. 偏相干方法分析及其工程应用[J]. 应用声学, 1994, 13(3): 25-30.

MA Zhong-cheng. Analysis and engineering application of the partial coherence method[J]. Applied Acoustics,1994,13(3):25-30.

[17]赵海澜,汪鸿振. 偏相干分析识别噪声源的计算[J].噪声与振动控制,2005(5):31-33.

ZHAO Hai-lan, WANG Hong-zhen. Calculation of identifying noise source based on partial coherence analysis [J]. Noise and Vibration Control,2005(5): 31-33.

[18]贝达特J S，皮尔索A G. ,著.凌福根，译.相关分析和谱分析的工程应用[M]. 北京：国防工业出版社，1983.

[19]贺旭东,陈怀海,申凡,等. 双振动台随机振动综合控制研究[J]. 振动工程学报, 2006, 19(2): 145-149.

HE Xu-dong, CHEN Huai-hai, SHEN Fan, et al. Study on dual-shaker random vibration test control[J]. Journal of Vibration Engineering, 2006, 19(2): 145-149.