集中驱动式纯电动车动力传动系统扭转振动研究
2015-12-30于蓬,章桐,孙玲等
第一作者于蓬男,博士生,1986年生
通信作者章桐男,教授,博士生导师,1960年生
邮箱:tzhang@fcv-sh.com
集中驱动式纯电动车动力传动系统扭转振动研究
于蓬1,2,章桐1,2,3,孙玲1,2,郭荣1,2(1.同济大学新能源汽车工程中心,上海201804;2.同济大学汽车学院,上海201804; 3.同济大学中德学院,上海201804)
摘要:针对电动车存在的动力传动系统扭转振动问题,提出综合考虑控制电机动态特性及传动系统间隙/柔性的机电耦合仿真方法。建立考虑电磁刚度影响的传动系统扭转振动集中质量模型,研究模态特性,并试验验证模型的正确性;考虑齿间侧隙及半轴柔性,搭建传动系统集中-分布质量模型进行动态响应仿真及试验验证;建立、仿真控制电机模型及机电耦合模型,获得转矩波动影响下传动系统扭转振动时频响应。结果表明,所提机电耦合仿真方法能呈现较丰富的动力学现象,有助于进一步揭示电动车传动系统扭转振动特性。
关键词:电动车;传动系统;扭转振动;机电耦合;转矩波动
收稿日期:2014-03-26修改稿收到日期:2014-05-29
中图分类号:U469.72文献标志码:A
Powertrain torsional vibration of a central-driven pure EV
YUPeng1,2,ZHANGTong1,2,3,SUNLing1,2,GUORong1,2(1. New Clean Energy Automotive Engineering Center, Tongji University, Shanghai 201804, China;2. School of Automotive Studies, Tongji University, Shanghai 201804, China;3. Sino-German College of Applied Sciences, Tongji University, Shanghai 201804, China)
Abstract:Aiming at driveline torsional, vibration of an EV, an electromechanical coupling simulation method considering dynamic characteristics of EV’s control motor and driveline clearance/flexibility was proposed. Firstly, the driveline lumped mass vibration model was established considering the influence of electromagnetic stiffness, its modal characteristics were studied and verified with tests. Then, the driveline lumped-distributed mass model was constructed considering backlash and flexibility of half shaft, the dynamic response simulation and test verification were conducted. Finally, the control motor model and the driveline electromechanical coupling model were built and simulated. The driveline torsion vibration response was obtained under the influence of torque ripple. Results showed that the proposed driveline electromechanical coupling simulation method can provide abundant dynamical phenomena, and its helpful to further reveal the driveline torsional vibration characteristics of an EV.
Key words:EV; driveline; torsional vibration; electro-mechanical coupling; torque ripple
集中驱动式纯电动车动力传动系统不同于传统内燃机车辆。该车动力系统与传动系统直接耦合,电机驱动速度快、转矩响应斜率大,易引发传动系统冲击及扭转振动,使电动车工作时出现纵向抖振现象[1-6]。文献[1-2]针对某燃料电池轿车存在的抖振现象,进行考虑多因素的动力传动系统非线性动态特性仿真,认为电机转矩波动是引起传动系统扭转振动的主要原因。类似的电驱动系统(轧机、水轮发电机等)扭转振动研究,多考虑电磁效应影响进行机电耦联仿真与控制[3]。文献[4]将机电耦联建模方法引入新能源汽车动力传动系统研究中,对该方法在电动车传动系统研究中的可适用性进行探讨。文献[5]在借鉴传统内燃机车辆传动系建模方法基础上,对模型分支及左右半轴扭转刚度不一致等与电动车传动系建模相关问题进行分析。本文在以往研究基础上,充分考虑电动车与传统车结构、操纵差异,提出电动车动力传动系机电耦合的建模方法,并进一步分析控制电机对考虑间隙、半轴柔性的传动系统影响,为电动车传动系统扭转振动解决提供指导。
1考虑电磁刚度影响的模态特性研究
1.1集中式驱动电动车动力传动系统

图1 动力传动系统模型 Fig.1 Drive train model
某电动汽车采用集中电机FF布置形式,集中驱动电机与减/差速器总成集成一起,动力通过二级齿轮传动进行减速增扭,经减/差速器及左右半轴驱动车轮。动力传动系统模型见图1。
1.2电磁扭转刚度计算
电动车由驱动电机定转子间产生的电磁转矩驱动,转矩施加会引发轴系冲击,继而在传动系统共振点引发轴系扭转振动。电磁转矩中电转角的一次项系数定义为电磁刚度[7]。由电机性能决定,电磁刚度将定子、转子联系一起,使定、转子及后续传动部件组成统一整体。研究对象采用正弦波永磁同步电机驱动传动系,可据适当变换计算该驱动电机在某工况下电磁刚度理论值。电磁转矩方程为
MM=p[ψfisq+(Lsd-Lsq)isdisq]
(1)
据定义计算电磁刚度,即
(2)
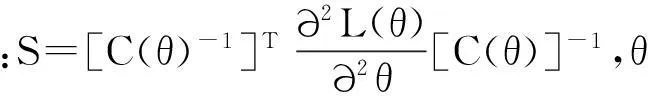
进一步推导得
(3)
研究电动车辆的驱动电机控制方法为最大转矩/电流控制,据交直轴电流分量与电磁转矩关系曲线,可求出电磁刚度值。工况选为电机转速3 000 r/min(不同工况电磁刚度值不同,电参数对电磁刚度灵敏度另文)、车速50 km/h、电机额定电压336 VDC,求得电磁刚度为6 Nm/rad。仿真所用参数含义及数值见表1。
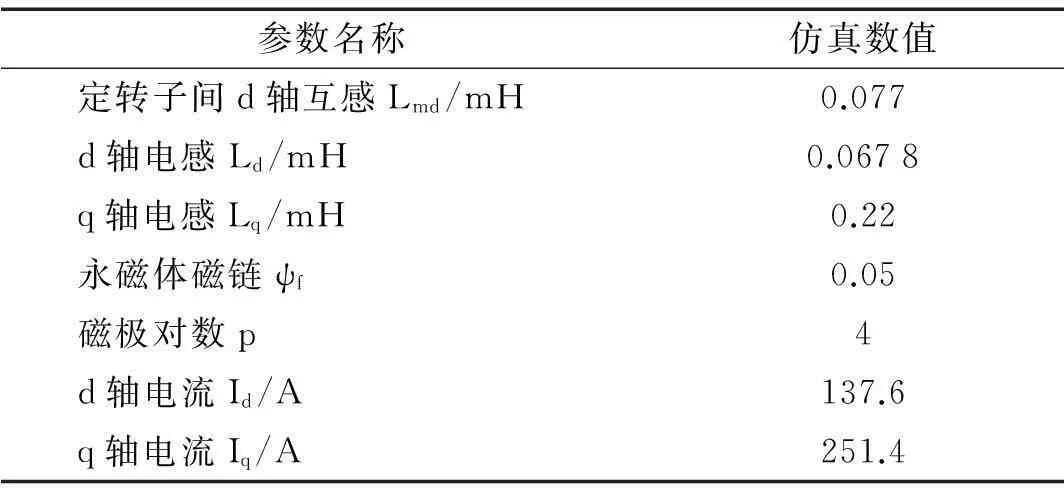
表1 电磁刚度计算所用参数
1.3考虑电磁刚度的分支模型
分支模型能反映左右车轮反向、同向共振两种不同模态,揭示更多模态特性。考虑电磁刚度作用,建立分支模型见图2,参数见表2。其中Ji为对应部件转动惯量(kg·m2),Ki为扭转刚度(Nm/rad)。
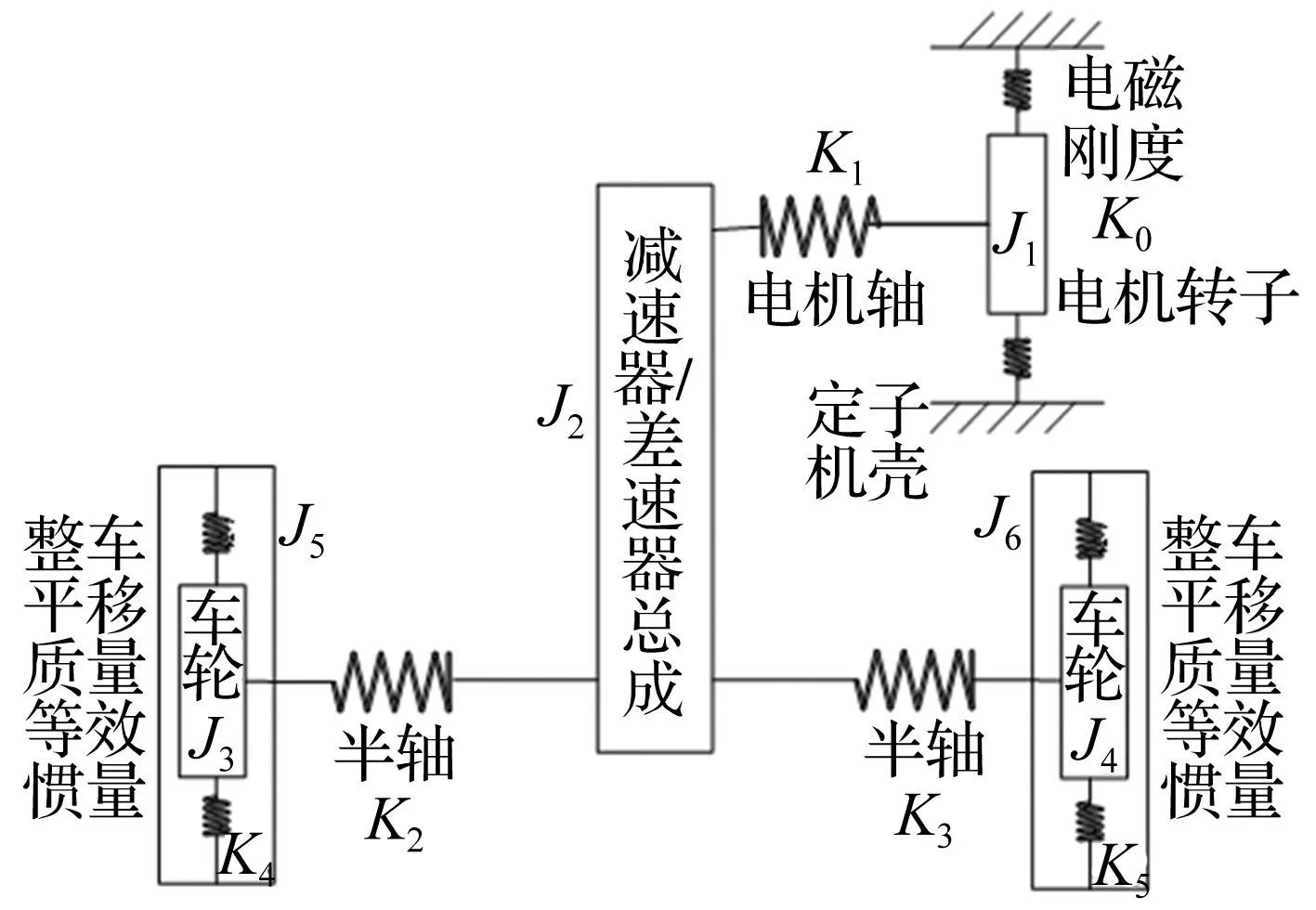
图2 考虑电磁刚度的分支模型 Fig.2 Branch model considering electromagnetic stiffness
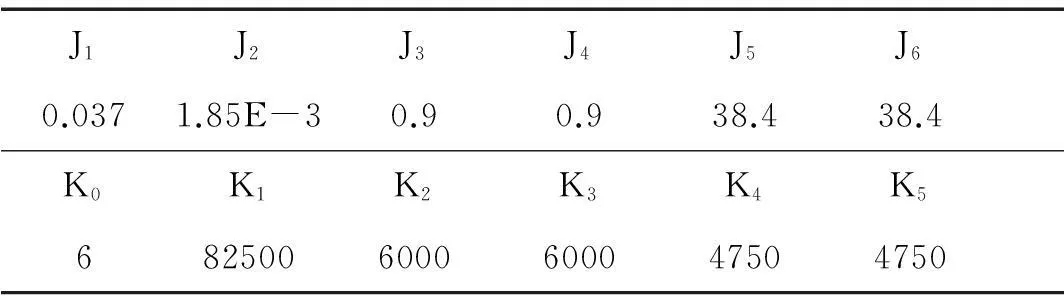
J1J2J3J4J5J60.0371.85E-30.90.938.438.4K0K1K2K3K4K56825006000600047504750
模型惯量、刚度矩阵为
无阻尼自由振动方程为
J{θ″}+K{θ}=0
(4)
求解所得系统固有频率及振型见表3。由表3知,考虑电磁刚度的传动系统分支模型可同时获得0.29、1.1两低阶特征频率,能全面反映传动系统低频率段固有特性。若不考虑电磁效应及分支影响,会丢失该两重要低阶特征频率[8]。由于电磁刚度计算值由工况决定,作为参考,同时给出6.5 km/h匀速时所得系统固有频率。

表3 传动系统固有频率
1.4转鼓稳态振动试验
测定某高速集中式驱动电动车在不同电机转矩下转速及车身纵向加速度响应。利用布置在座椅导轨处的加速度传感器采集整车纵向振动信号;通过CANCASE/CANAPE软硬件采集电机转速、转矩及车速等数据。振动试验布置见图3。

图3 整车匀速振动试验 Fig.3 Vibration test under steady condition
以电机加速到3 000 r/min(车速50 km/h)工况为例,控制加速踏板到一定角度后保持,直到车速达到50 km/h。对所测稳态时域信号进行FFT变换,得到0~30 Hz范围内频域响应。图4(a)为座椅导轨处沿整车前进方向频域结果。由图4(a)可知,幅值最大共振点对应频率值依次为0.32 Hz、0.94 Hz、8 Hz、16 Hz、23 Hz,与仿真的0.29 Hz、1.1 Hz、7.45 Hz、18.5 Hz、21 Hz接近,说明传动系模型的正确性。需指出的是,用车身纵向加速度结果验证传动系统模态特性方法属于间接验证,因传动系统在接近其固有频率强迫激励下会发生扭转共振,引起车轮转速及角加速度剧烈波动,进而表现为整车纵向平移方向速度、加速度产生较大波动。若条件允许,用专业的扭转振动测量设备能更准确、直观验证传动系统的扭转振动频率。作为参考给出6.5 km/h工况下试验结果见图4(b),其中峰值与仿真结果吻合较好,其余各工况下结果见表4。由表4知,电磁刚度引发的0.3 Hz振峰始终存在,高于不驱动时的0.15 Hz;分支引发的1 Hz振峰始终存在,6.5 km/h时由电机基频引发共振,同时引起传动系统7.99 Hz共振;8 Hz为传动系统整体扭转振动频率,52 km/h时由电机基频引发共振;19 Hz、22 Hz为左右车轮局部模态,由车速基频的2倍频引发共振;25Hz为主副车架一阶弯曲扭转模态值,由轮速基频的2倍频引发;3.3 Hz、12.2 Hz为悬挂车身及车轮系统固有频率。

图4 座椅导轨频域信号 Fig.4 Frequency domain signal of seat rail
另外,汇总各频率点峰值看出,轮胎转速基频引发振动幅值一般<0.35 m/s2,引发传动系共振时则>0.5 m/s2,如传动系1 Hz、8 Hz,悬挂3.3 Hz;轮胎转速基频二倍频引发振动幅值一般<0.2 m/s2,引发共振时则>0.2 m/s2,如传动系19 Hz、22 Hz,悬挂12~16 Hz;1倍电流频率转矩波动引发共振时幅值达0.35 m/s2,2、3倍电流频率转矩波动引发共振时幅值达0.25 m/s-2,通常转矩波动所致共振在座椅上引起的x方向振动幅值<0.2 m/s2;转矩波动对传动系影响在该频率范围较少,如<5 km/h(此时一倍波动达20 Hz),对高速如>10 km/h(此时一倍波动达40 Hz)及更高频率影响后述。

表4 稳态工况下频域分析结果汇总
2传动系扭转振动集中-分布混合模型
在集中质量模型基础上,建立考虑更详细机械参数影响的混合模型用于动力学响应分析。将整个动力传动系统分为电机转子、一级齿轮副、二级齿轮副、车轮、整车等效惯量及各轴段进行模块化建模。建模过程充分考虑齿轮传动中的啮合刚度、齿间侧隙、半轴柔性影响[9]。各部件动力学方程建立过程如下。
(1)电机转子动力学方程
Jrθ″=Te-Tl
(5)
式中:Te为电机转子输入转矩;Tl为电机转子负载转矩;Jr为电机转子惯量。
(2)电机轴动力学方程
Tm=c(w1-w2)+k(θ1-θ2)
(6)
式中:Tm为轴输出端转矩;c为轴段阻尼;k为轴段刚度。
(3)减/差速器总成
据齿轮啮合动力学模型建立齿轮传动模型。将两级齿轮副之间的轴视为无质量弹性轴。不考虑齿轮啮合误差、支撑部件及齿轮本身弹性变形情况下,动力学方程为
(7)
(8)
x=Raθa-Rpθp
(9)
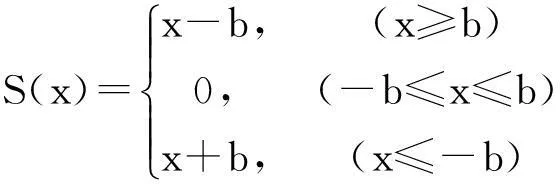
(10)
式中:Ia,Ib为主从动齿轮转动惯量;Ta,Tb为作用于主从动齿轮的转矩;Ra,Rp为主从动齿轮节圆半径;cm为齿轮副啮合阻尼;km为齿轮副综合啮合刚度;x为轮齿相对位移;b为齿间侧隙;S(x)为考虑齿侧间隙的轮间相对位移。
(4)车轮及整车质量
忽略轮胎非线性特性,将整车等效惯量直接加到轮胎胎体上进行传动系统动力学及整车运动的等效模拟。车轮动力学方程为
Jaθa″=Tay-Tby
(11)
Jbθb″=Tby-FxR
(12)
(13)
式中:Tay为驱动力矩;Tby为轮毂与胎冠间作用力矩;Ja为轮毂惯量;Jb为胎体及整车等效惯量;Fx为整车滚动阻力。
(5) 离散化半轴
集中质量模型仅对振动系统低频段有较高精度。为更好反映电机、间隙等非线性因素对动力传动系统扭转振动影响,建立离散化半轴分布质量模型,分布质量轴微小分段扭矩、角度传递过程见图5。与传动系统其它部件连接可得动力传动系统集中-分布质量综合模型。
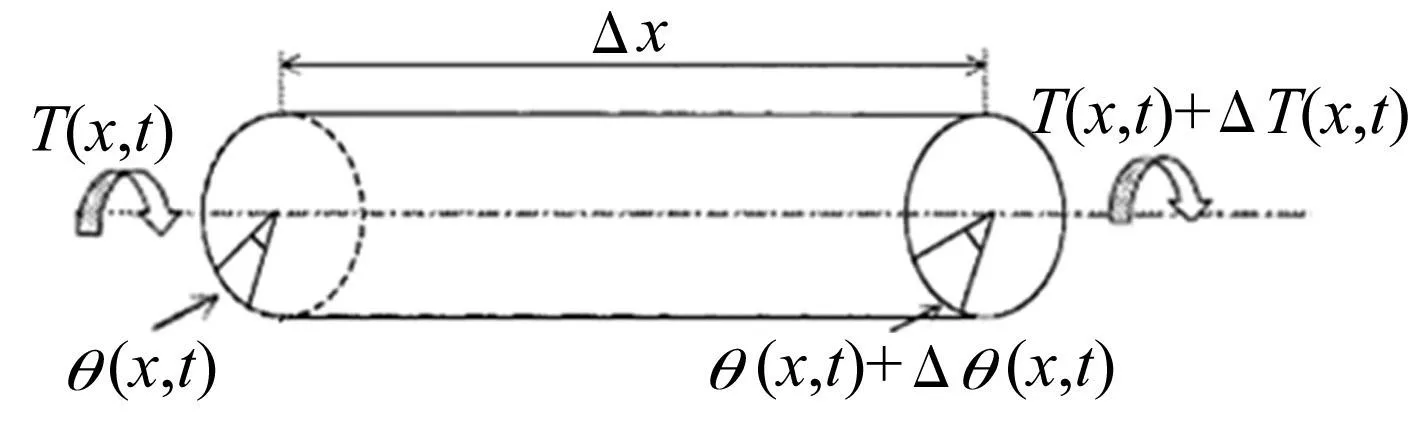
图5 分布质量微段 Fig.5 Distributed mass micro segment
微段扭转方向动力学方程为
(14)
式中:Jρ为每米轴的转动惯量。
将轴扭转方向的传递函数变换到Z域得
(15)
(16)
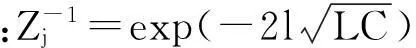
将离散化半轴创建为子模块,并与其余集中质量部件子模块连接得到最终集中-分布质量动力传动系统模型,见图6。

图6 传动系统集中-分布质量模型 Fig.6 Lumped-distributed mass model of driveline
为验证模型的准确性,取试验所测急加速到50km/h工况电机转矩见图7。施加到传动系统集中-分布质量系统模型进行仿真,得电机转速仿真曲线,见图8。由图8知,实测转矩输入下,电机转速仿真及试验曲线吻合较好,说明该集中-分布质量模型能基本反映实车动力传动系统扭转振动响应特性。初始过程中幅值差异可能因忽略电机动态与传动系统耦合作用原因。
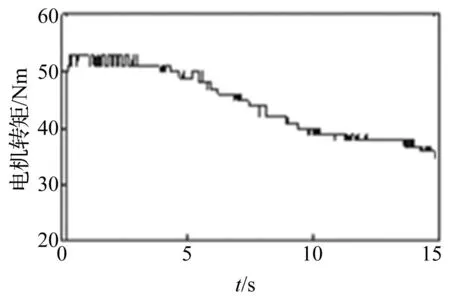
图7 试验电机转矩 Fig.7 Tested motor torque
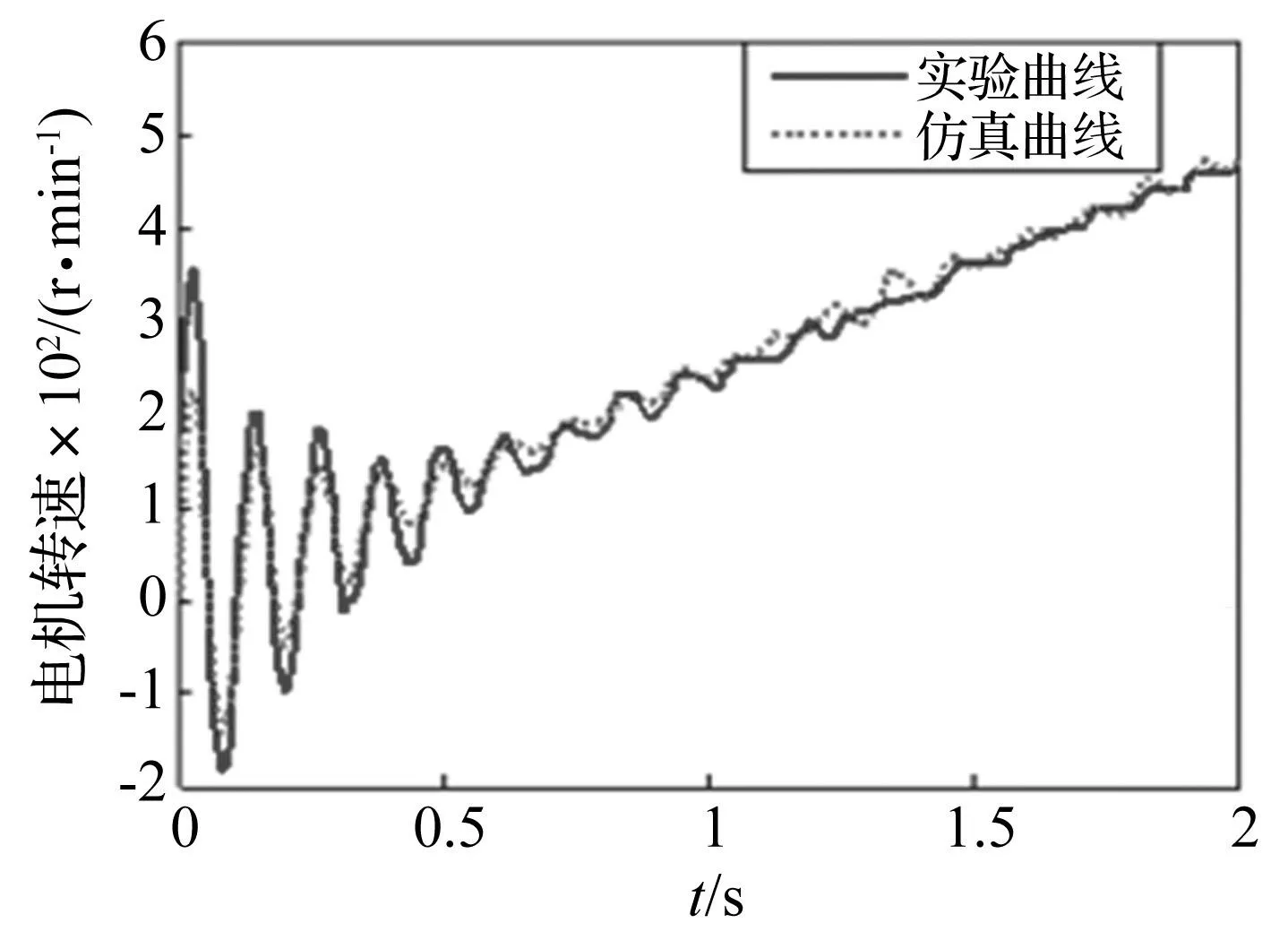
图8 电机转速响应 Fig.8 Motor torque response
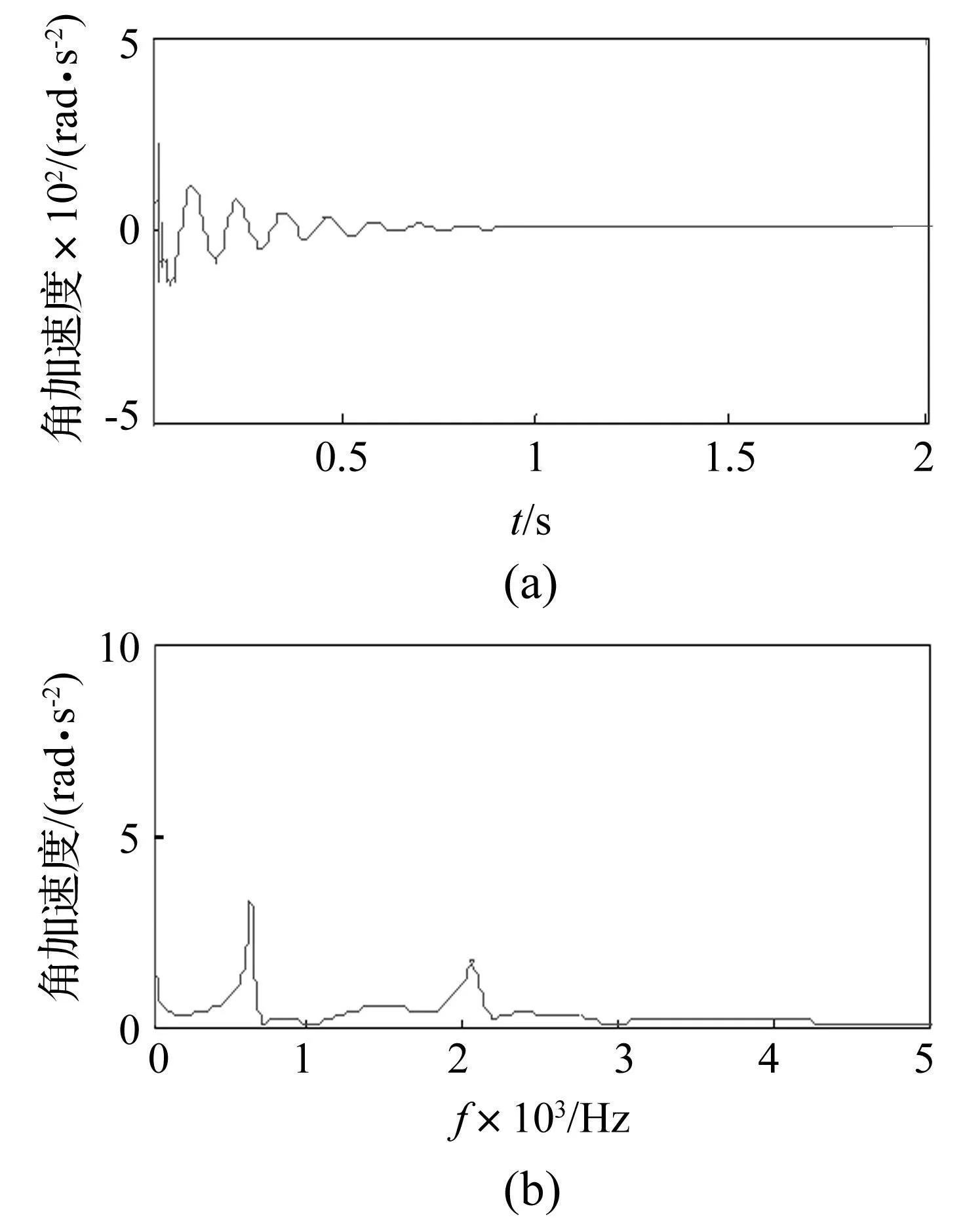
图9 集中质量模型减/差速器输出端角加速度 Fig.9 Differential/reducer output angular acceleration of lumped mass model
设电机转子处转矩输入为50 Nm,对比集中质量模型与集中-分布质量模型扭转振动响应结果,对减速器输出端角加速度进行分析,见图9、图10。对比两图可知,两种模型时域特性基本一致,但在频域特性呈现较大差异。集中-分布质量模型动力学现象更丰富,尤其在2 800 Hz处存在明显峰值。进一步甄别该频率为离散化半轴柔性引发的传动系统高阶固有频率;集中质量模型则未反映出该频率峰值。另外,630 Hz、2 000 Hz峰值由减/差速器齿轮传动系统局部模态产生。
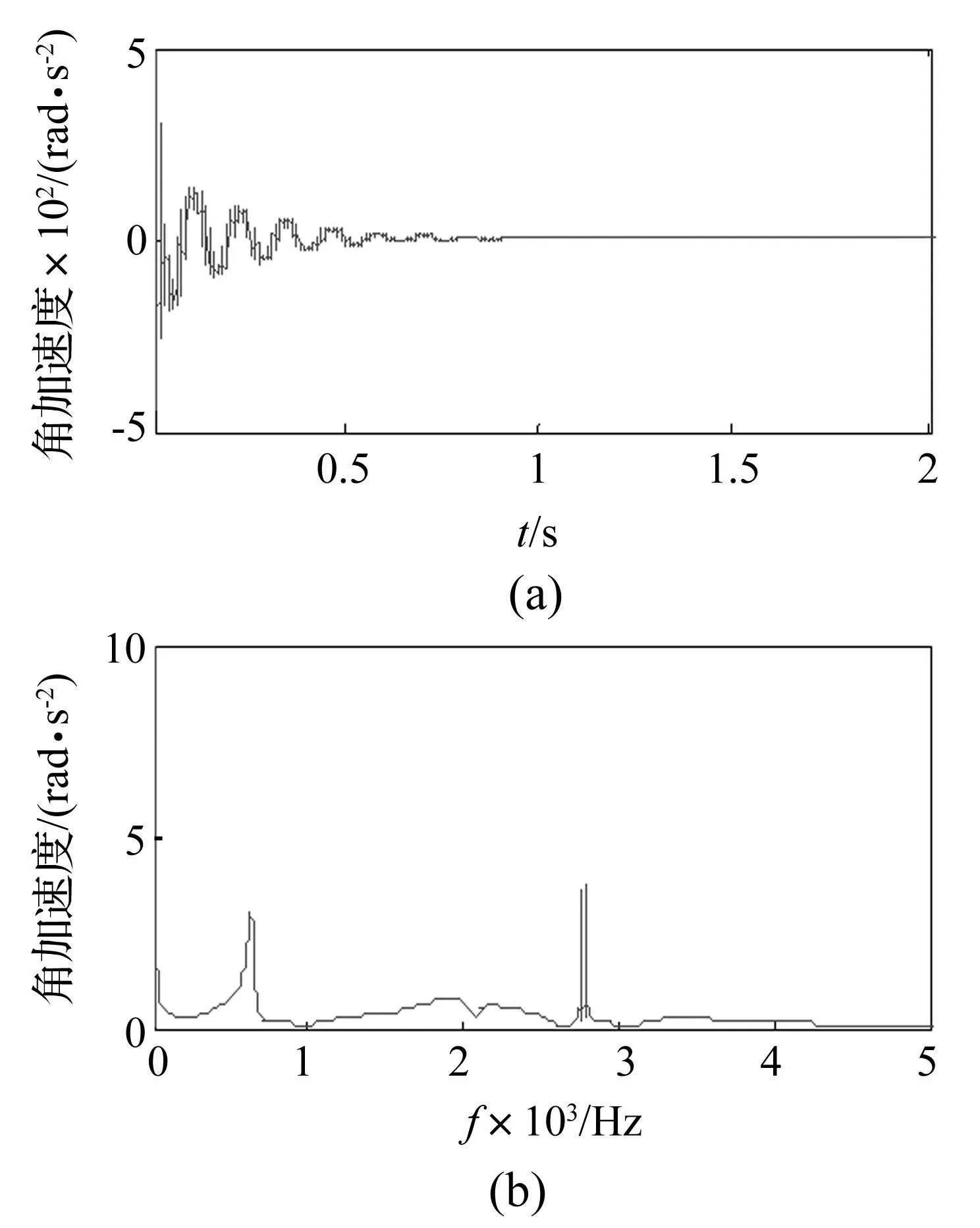
图10 集中-分布质量模型减/差速器输出端角加速度 Fig.10 Differential/reducer output angular acceleration of lumped-distributed mass model
3机电耦合仿真模型
3.1转矩波动特性
为反映电机动态与传动系统耦合的相互作用,考虑搭建控制电机模型。归纳永磁同步电机的转矩波动特性[9,15],主要从结构、控制两方面总结,见表5、表6。

表5 结构因素产生的转矩波动

表6 控制因素产生的转矩波动
对应汇总结果,对座椅导轨处所测振动信号进行阶次分析,获得4阶、8阶、12阶、16阶、24阶转子基频的转矩波动,分别由1倍、2倍、3倍、4倍、6倍电流频率波动引起,试验结果见图11。后续分析主要考虑由控制因素引起的转矩波动对传动系统动响应影响。
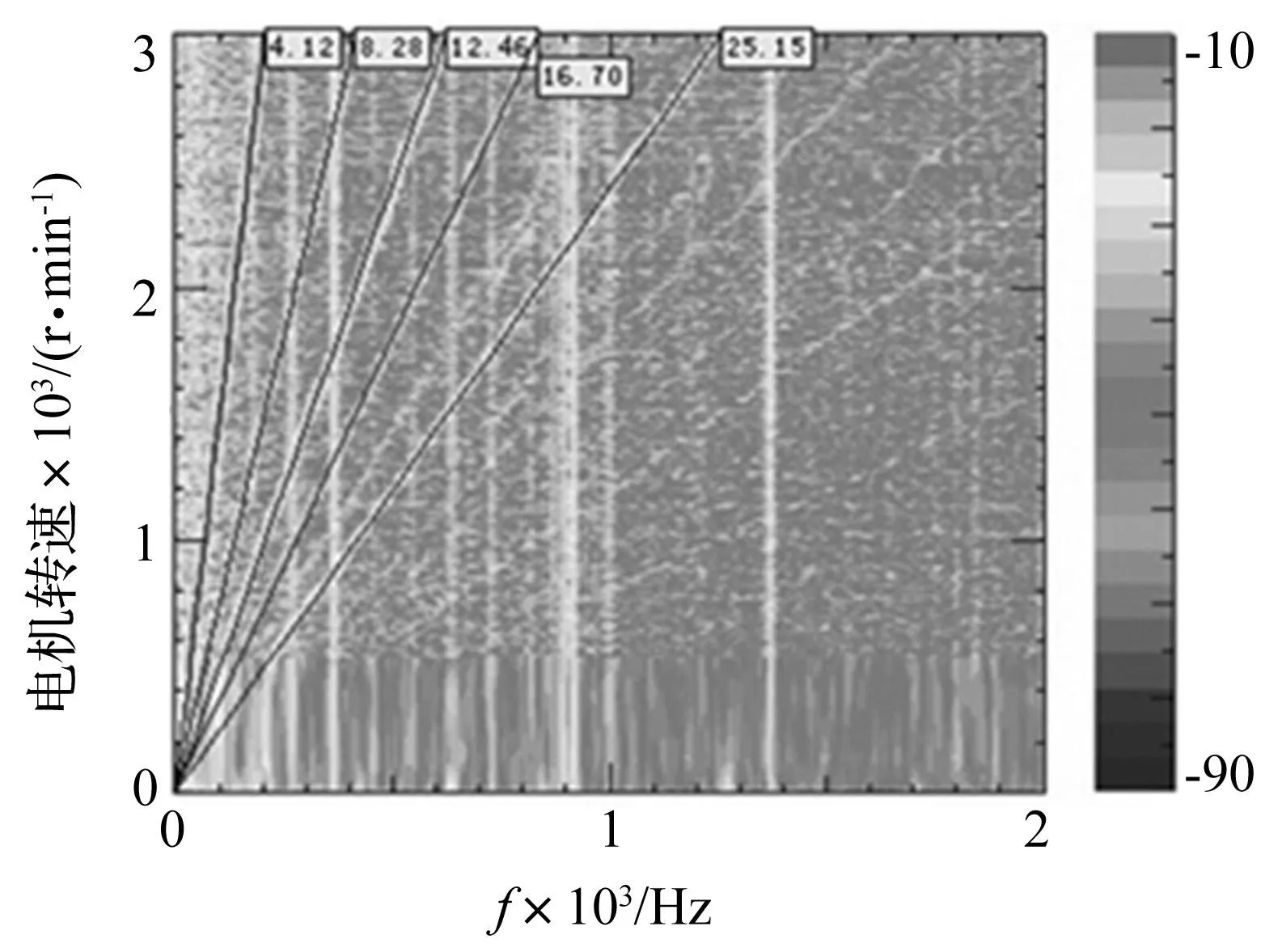
图11 座椅导轨加速度阶次信号 Fig.11 Acceleration order signal of seat rail
3.2控制电机建模
永磁同步电机采用SVPWM(空间矢量调制)方法,控制策略采用最大转矩电流比控制,搭建基于矢量控制的电机模型,见图12。
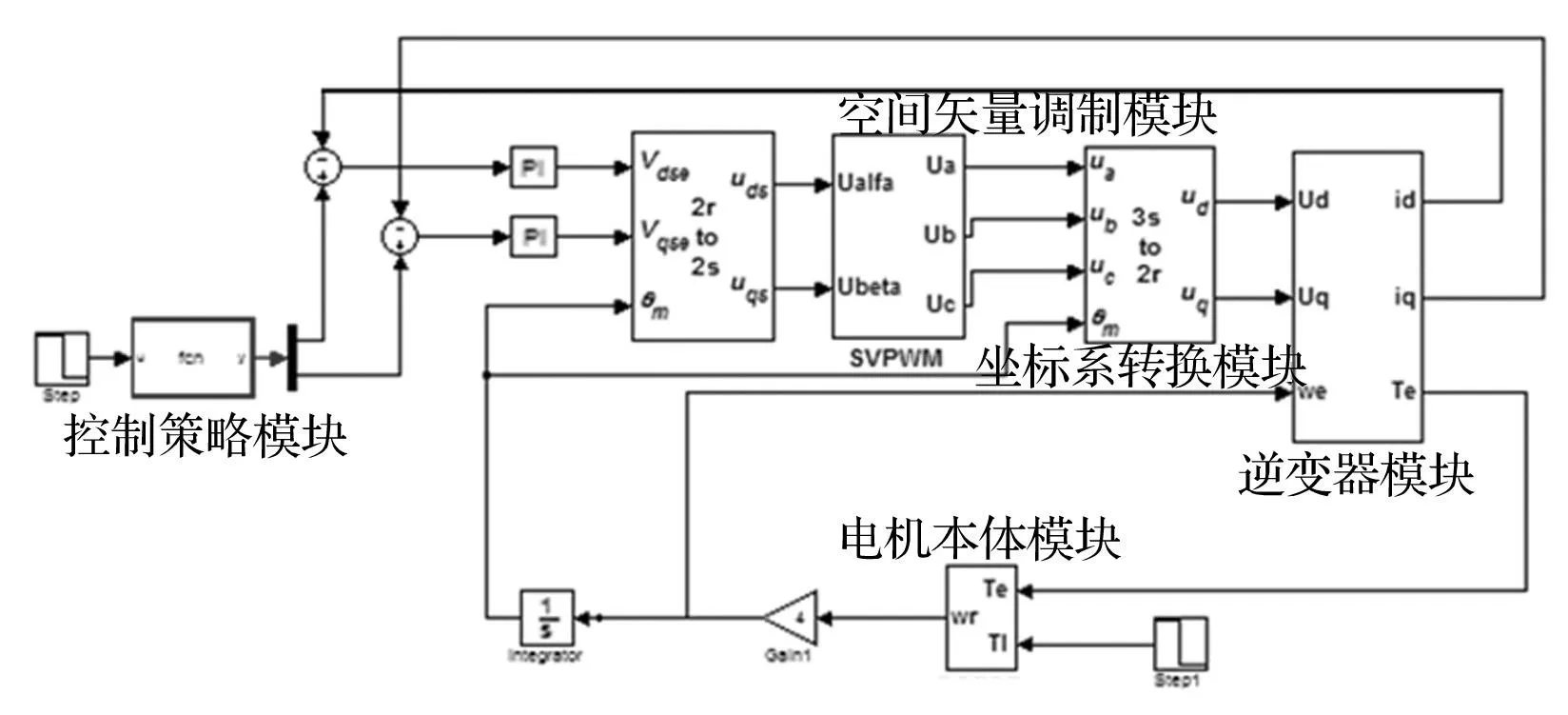
图12 永磁同步电机矢量控制模型 Fig.12 Permanent magnet synchronous motor model
采用最大转矩电流比控制时,转矩、定子电流之间满足关系式为
Te=1.5np(ψfiq+(Ld-Lq)idiq)
(17)
(18)
模型中控制策略模块通过线性插值获得对应转矩指令下参考电流。参考电流与实际电流差值经PI调节后获得参考电压,d、q轴的参考电压据传感器采集的转子位置角,通过Park反变换得到定子两相静止坐标系下参考电压供空间矢量调制使用,经调制得到逆变器开关脉冲信号。开关脉冲信号送入逆变器输出接近于正弦波的电压驱动电机转动。
3.3机电耦合建模及仿真
将图12中驱动控制电机模型与图6传动系统模型结合,获得考虑电机动态、齿间侧隙、半轴柔性的机电耦合综合仿真模型。即将由控制电机产生的电磁转矩作用到动力传动系统的电机转子端,并将电机转子转速作为反馈,转换成电角度、角速度后用于电机模块及电压/电流转换模块。
据试验、理论分析结果,仿真过程综合考虑电流的直流偏移误差、增益误差、定子电流谐波分量及磁场非正弦影响,设直流偏移误差ΔA=-0.2 A, ΔB=0.2 A,电流增益误差Ka=-0.01,Kb=0.01,定子电流2次谐波幅值为0.4 A,磁场磁链6次谐波幅值为磁链基值的0.02倍。
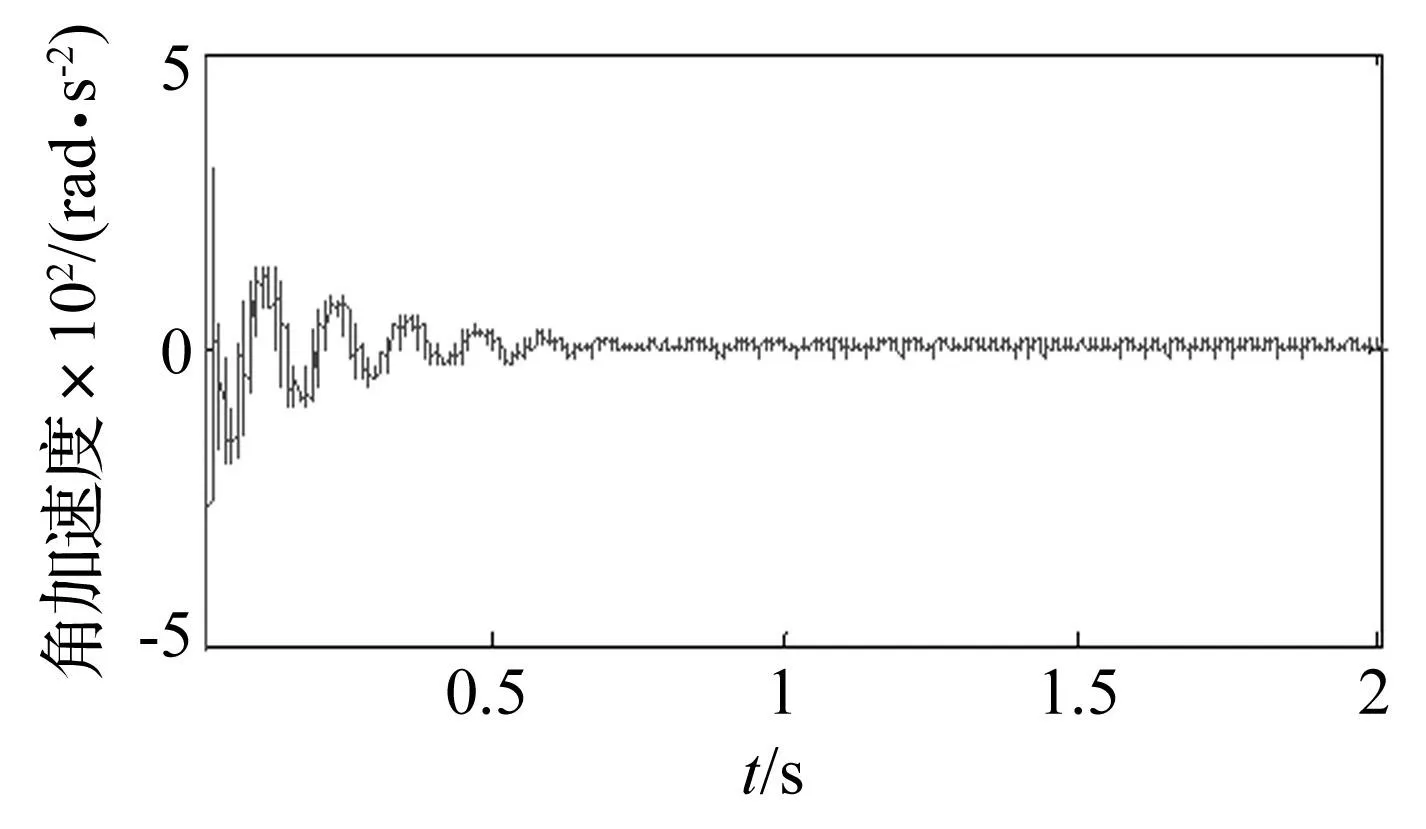
图13 减/差速器输出端角加速度 Fig.13 Differential/reducer output angular acceleration of electro-mechanical coupling model
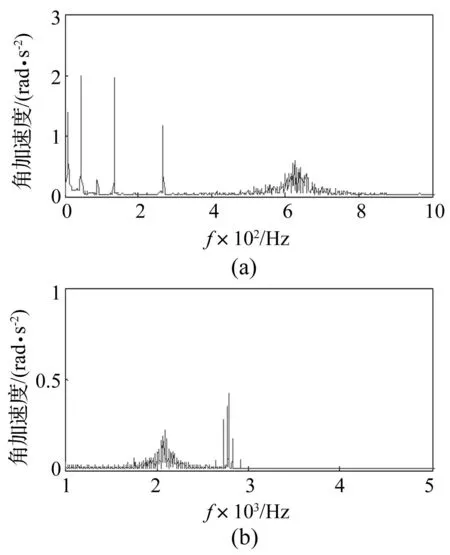
图14 减/差速器输出端角加速度 Fig.14 Differential/reducer output angular acceleration of electro-mechanical coupling model
选50 Nm驱动力矩对传动系统进行加速,当车速达到10 km/h时控制转矩使电动车以10 km/h稳态运行,此时电流频率为45 Hz。减/差速器输出端角加速度时域仿真结果见图13,与图9、图10不考虑驱动电机动态及控制因素引发转矩波动时结果相比,动态响应结果更丰富。对恒定转速下信号进行频域分析,结果见图14。对比图9、图10频域分析结果可知,在传动系统固有频率630 Hz、2 000 Hz及2 800 Hz处,均发生较大变化,体现出更丰富的机电耦合动力学现象。而在45 Hz、90 Hz、135 Hz及270 Hz处产生明显峰值,分别由电流基频45 Hz的1倍、2倍、3倍及6倍转矩波动引起,体现出转矩波动对传动系统动态特性影响。
4结论
(1)电磁刚度及分支引起的电动车动力传动系统低阶固有频率(0~2 Hz)会导致车辆传动系统在低阶特征频率对应的电机转速、车速下产生共振,引发整车纵向振动。所提综合考虑电磁刚度及分支的传动系统建模方法,有助于揭示电动车辆传动系统存在的整车低频纵向抖振(“慢动”)问题。
(2)考虑半轴柔性的传动系统集中-分布质量模型,可在时域上反映更丰富的动力学现象,也可在频域上反映间隙等非线性因素对传动系统高阶次频域响应特性影响。有助于进一步解决集中式驱动电动车传动系统存在的纵向高频扭转振动(“微冲”)问题。
(3)电动车传动系统为典型的机电一体化系统,其扭转振动问题可通过主动控制方式解决。基于控制电机模型及集中-分布质量传动系统模型的机电耦合综合模型仿真,可全面揭示电动车传动系统在电气因素、机械因素耦合作用下的瞬态、稳态振动特性,为解决电动车动力传动系统存在的扭转振动问题提供了有效仿真、优化平台,为电动车传动系统主动扭转振动控制奠定基础。
参考文献
[1]张立军, 司杨, 余卓平. 燃料电池轿车动力传动系统非线性动态特性仿真分析[J]. 机械工程学报,2009,2:62-67.
ZHANG Li-jun,SI Yang,YU Zhuo-ping. Numerical investigation into nonlinear dynamical characteristics of fuel cell vehicle powertrain system[J]. Journal of Mechanical Engineering,2009,2:62-67.
[2]张立军,郑鹏,孟德建,等.混合动力轿车纯电动模式起步时纵向抖振的试验研究与控制[J]. 汽车工程,2013,35(3): 212-218.
ZHANG Li-jun, ZHENG Peng, MENG De-jian, et al. Experimental study and control of longitudinal flutter during vehicle starting with motor drive mode for hybrid electric car[J]. Automotive Engineering, 2013,35(3): 212-218.
[3]Slobodan N, Member V C. Suppression of torsional oscillations in a high-performance speed servo drive[J]. EEE Transaction on Industrial Electronics,1998,45(1): 108-117.
[4]Yu Peng, Zhang Tong, Liu Pu-hui. Mechanical and electrical coupling vibration characteristic analysis of powertrain system for electric driven vehicle[J]. Applied Mechanics and Materials, 2012, 224: 385-388.
[5]王泽勇,于蓬,章桐.电动车动力传动系扭振模型分支问题研究[J].上海汽车,2013,3:4-8.
WANG Ze-yong, YU Peng,ZHANG Tong. Research on electric vehicle power train torsion vibration branch modeling[J]. Shanghai Auto, 2013,3: 4-8.
[6]Xu Jian-fu, Yu Peng, Zhang Tong, et al. Design of torsional vibration controller for motor-gearbox/differential drive system of electric vehicles[J]. Applied Mechanics and Materials, 2013, 437: 56-61.
[7]Ooi B T, Low T S. Electromechanical spring stiffness from the small perturbation linearized equations of generalized machine theory[J]. IEEE Transactions on Energy Conversion, 1990,5(2): 374-379.
[8]陈贵清,邱家俊. 水轮发电机组转子轴系扭振零阶固有频率的计算和分析[J].商丘师专学报,1999,15(2):267-273.
CHEN Gui-qing,QIU Jia-jun. The calculation and analysis of zero-order frequency of hydro-generator rator under torsional vibration[J].Journal of Shangqiu Teachers College,1999,15(2): 267-273.
[9]Farshidianfar A, Ebrahimi M, Bartlett H. Hybrid modelling and simulation of the torsional vibration of vehicle driveline systems[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2001, 215(2): 217-229.
[10] Li Tou-zhu, Gordon Slemon. Reduction of cogging torque in permanent magnet motors[J]. IEEE Transactions on Mechatronics,1988,24(6):2901-2903.
[11]Colamartino F, Marchand C, Razek A. Torque ripple minimization in permanent magnet synchronous servodrive[C]. IEEE Electric Machines and Drives Conference Record, 1997:WB2/5.1-WB2/5.3.
[12]Chen Shao-tang. Controller induced parasitic torque ripples in a PM synchronous motor[C]. IEEE Industry Applications Conference, 2000: 1273-1280.
[13]Islam Mohammad S,Rakib I,Tomy S.Experimental verification of design techniques of permanent-magnet synchronous motors for low- torque-ripple applications[J]. IEEE Transactions on industry applications,2011,47 (1) : 88-95.
[14]Vladan P,Romeo O,Stankovic Aleksandar M, et al. Design and implementation of an adaptive controller for torque ripple minimization in PM synchronous motors[J].IEEE Transactions on Power Electronics,2000,15(5) : 871-880.
[15]马琮淦,左曙光,谭钦文,等.电动车用永磁同步电机非线性扭转振动模型[J].振动与冲击,2013,32(12):131-134.
MA Cong-gan,ZUO Shu-guang,TAN Qin-wen, et al.Non-linear torsional vibration model of a PMSM for electric driven vehicle[J].Journal of Vibration and Shock,2013,32(12):131-134.

