基于 GEP 的爆破峰值速度预测模型

第一作者史秀志男，博士，教授，博士生导师，1966年生

邮箱：425837528@qq.com

基于GEP的爆破峰值速度预测模型

史秀志1，陈新1，史采星1，刘博1，张迅2(1.中南大学资源与安全工程学院，长沙410083；2.中南大学软件学院，长沙410083)

摘要：针对施工中爆破振动危害严重、振动峰值速度难以预测问题，选用基因表达式编程(Gene Expression Programming， GEP)算法以MyEclipse为开发工具，建立基于GEP的爆破峰值速度预测模型。取实测数据进行预测，并与萨道夫斯基经验公式与模糊神经网络模型预测结果对比。结果表明，三者平均相对误差分别为8.8%、11.3%及27.9%。由此证明GEP模型预测爆破峰值速度可行，亦为爆破振动预测提供新思路。

关键词：爆破振动；爆破峰值速度；GEP；预测

基金项目：国家科技支撑计划项目(2013BAB02B05)

收稿日期：2014-03-25修改稿收到日期：2014-05-06

中图分类号:TD235文献标志码：A

Prediction model for blasting-vibration-peak-speed based on GEP

SHIXiu-zhi1,CHENXin1,SHICai-xing1,LIUBo1,ZHANGXun2(1. School of Resources and Safety Engineering, Central South University, Changsha 410083, China；2. School of Software, Central South University, Changsha 410083, China)

Abstract:In order to predict the peak particle velocity of blasting vibration, the measured data of an open pit bench blasting were selected and a prediction model of peak particle velocity of blasting vibration was established based on GEP with My Eclipse as a development tool. By comparing the forecasted data and the measured ones, the average relative errors of the results of three methods including GEP, the fuzzy-neural network and the experience formula were 8.8%, 11.3% and 27.9%, respectively. The predicted results demonstrated that GEP is feasible and it provides a new way for predicting the peak particle velocity of blasting vibration.

Key words:blasting vibration; peak particle velocity of blasting vibration; gene expression programming (GEP); predict

工程中爆破振动产生的负面效应不可避免。因此爆破前对其振动特征参量进行预测十分必要[1]。爆破振动影响因素众多，各因素间存在复杂的非线性关系。传统的萨道夫斯基公式仅考虑段药量、爆源距两参数，处理过于简单，难以确定相关系数，存在不科学性及预测误差较大等缺点。引用模糊神经网络虽一定程度上能提高学习速度及识别精度，但神经网络训练效果的好坏对初始权值及阈值的选取依赖性较强，且需大量训练样本，否则即使收敛到全局最小，也不能保证有较高精度[2-3]。基因表达式编程算法具有强大的全局搜索寻优能力，在面对多参数非线性问题时也具有极强的函数发现能力及很高的训练效率，能发掘较准确的预测公式。本文将基因表达式编程用于爆破峰值速度预测，取得较好效果。

1GEP简介

1.1GEP定义

基因表达式编程(Gene Expression Programming， GEP)由Ferreira于2001年借鉴生物遗传基因表达规律提出的基于基因型及表现型自适应演化算法数据挖掘技术。其在遗传算法(Genetic Algorithms，GA)、遗传程序设计(Genetic Programming，GP)基础上进化发展而来。结合GA的简单线性染色体思想与GP中所用大小、形状不同的分叉结构思想，遗传过程中表现为定长线性字符串易于遗传操作，并具有非线性的树结构，从而达到简单编码解决复杂问题之目的，使其在速度上较GA与GP提高100倍～60000倍[4-6]，计算精度亦大幅提高。目前GEP已在多领域得以应用及发展。如：袁晖等[7]提出的基于GEP自动聚类算法视频关键帧提取方法；王超等[8]将GEP算法用于变压器故障诊断；杜冬等[9]建立基于GEP的四维飞行轨迹预测模型；孟艳等[10]将GEP算法用于桁架结构优化设计。目前尚无将GEP算法用于爆破峰值速度预测。

1.2GEP基因及染色体结构

GEP染色体由一个或多个基因通过连接符作用成为整体，为固定长度的字符串，由头、尾部组成。头部元素∈{函数集F}∪{终止集T}，尾部元素∈{终止集T}。其中F由求解问题需要的所有函数运算符组成，T由描述问题解的已知符号、变量或常数组成。头部长度h及尾部长度t需满足关系为

t=h(n-1)+1

(1)

式中：n为函数集F中函数最大操作数。t与h所具有的特殊关系，使基于基因型个体的遗传操作有很好的合法性[11]。

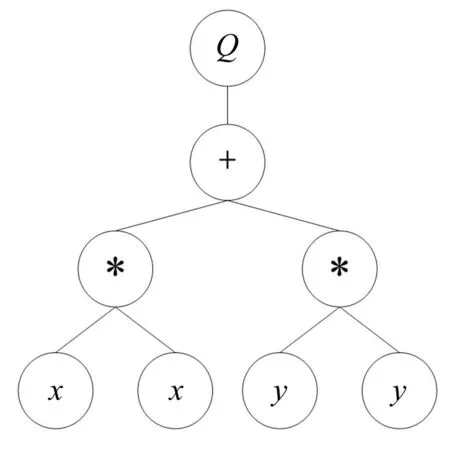
图1　表达式树结构 Fig.1 The expression trees structure

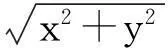
1.3GEP遗传算子及步骤

基因表达式编程核心及精髓为遗传操作。其中，算子通常选用轮转赌盘算子，据染色体适应度值大小计算染色体进入子代种群概率。变异操作可在染色体任何位置进行，只要保持染色体组织结构不变，经变异后产生的新个体均为合法程序。插串算子为选中基因的一个片段，将其迁移到基因的另个位置，按能否将特定遗传序列插入基因头部首位分为插串算子与根插串算子。重组作为交换父代染色体间等位基因，有三种重组操作方式，即单点重组、两点重组及基因重组[12]。

GEP选合适的函数符及终止符对种群进行初始化，算法随机产生一个种群对染色体进行解码，计算适应度值，再对染色体选择、复制、变异、插串、根插串、基因重组、单点重组、两点重组等遗传操作，产生新的个体形成子代种群。通过赌盘方式选择适应度高的个体重复遗传操作，直至适应度值达最大值或进化代数达规定值时结束[13]。具体流程见图2。

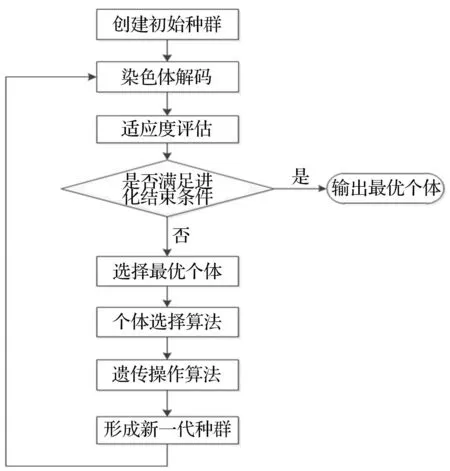
图2　GEP算法流程 Fig.2 GEP algorithm process

1.4GEP适应度函数

适应度函数能计算种群中染色体适应环境的能力，据个体适应能力对种群进化进行指导。两种分别以绝对误差、相对误差计算适应度函数表达式[14]为

(2)

(3)

式中：fi为第i个染色体适应度值；M为常量，为控制适应度fi的取值范围；Ct为计算样本量；C(i,j)为第i个染色体计算第j个样本时的函数值；Tj为第j个样本实际值。

2GEP峰值速度预测模型建立与应用

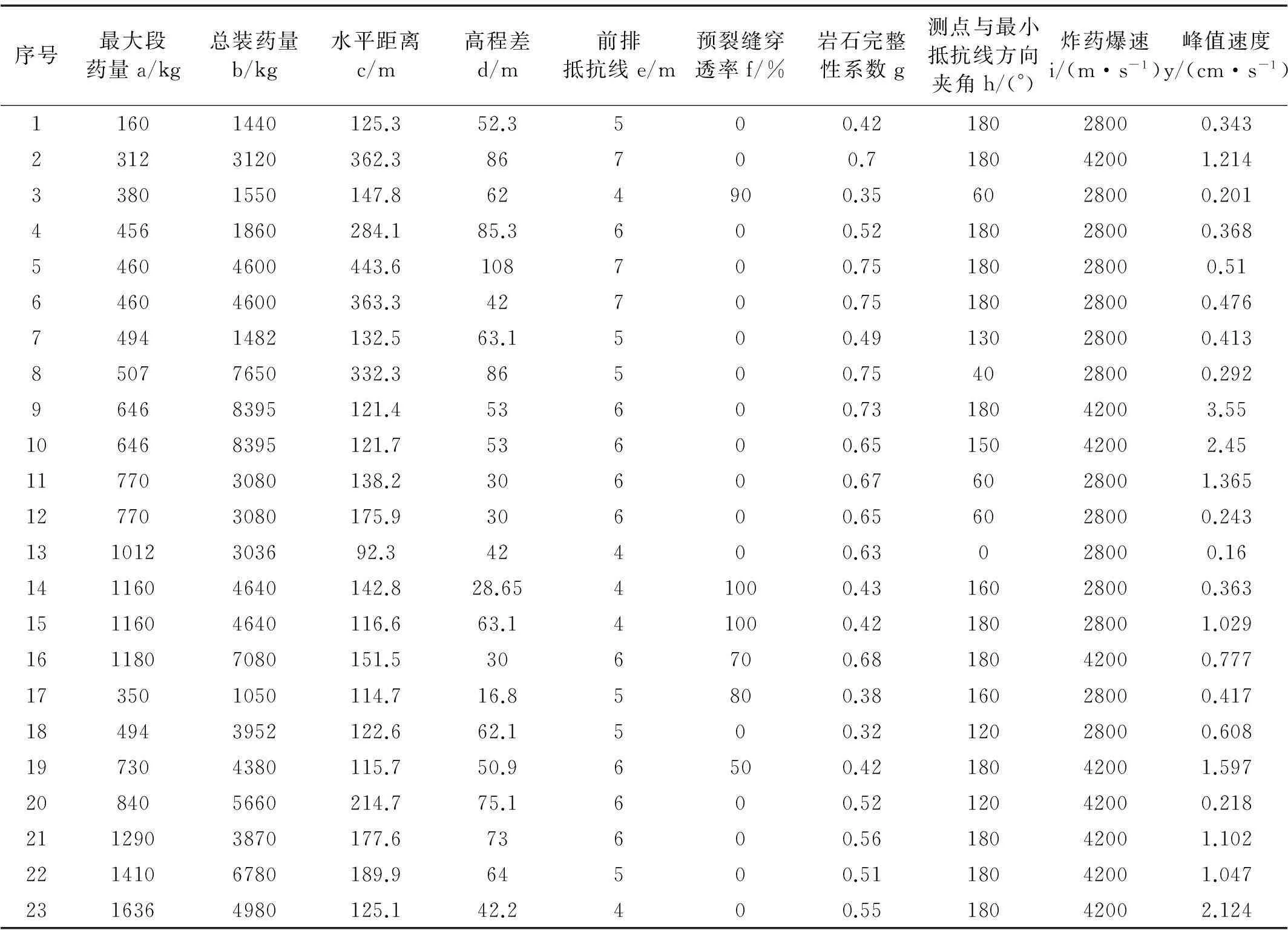
以铜录山露天台阶爆破为例，现场试验测定影响爆破振动峰值速度的主要因素有：最大段药量、总装药量、水平距离、高程差、前排抵抗线、预裂缝穿透率、岩体完整性系数、测点及最小抵抗线方向夹角、炸药爆速[15]。为验证预测模型的有效性及可行性，对铜录山露天台阶爆破进行研究的23组实测数据进行分析，其中前16组用作训练，后7组进行预测，见表1。由于表1中所用数据单位不同，且部分数值间差距较大，不利于计算，故对表1数据用标准差归一化方法进行无量纲化处理，即

(4)

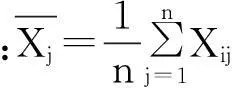
对预测后计算结果进行反归一化处理[16]，即

(5)

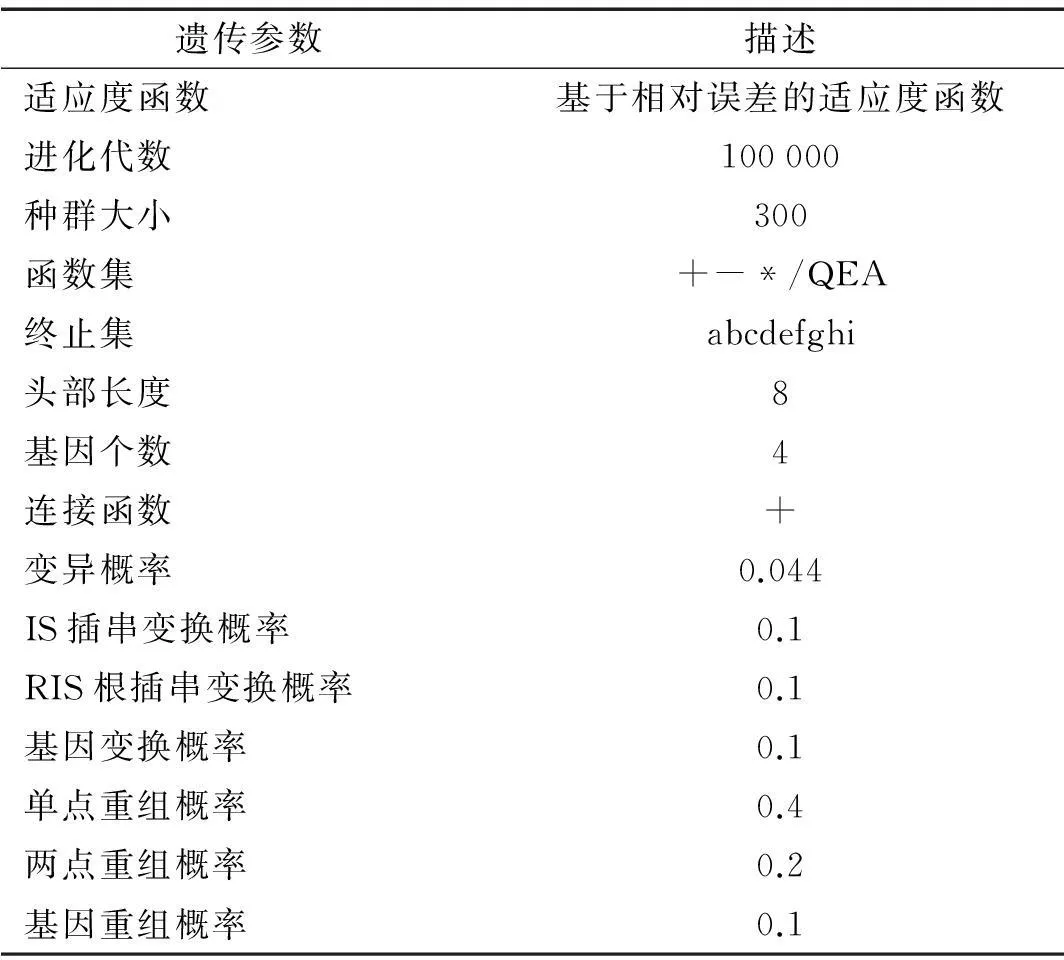
表2　遗传参数

2.1GEP预测模型建立

GEP建模选取最大段药量a、总装药量b、水平距离c、高程差d、前排抵抗线e、预裂缝穿透率f、岩体完整性系数g、测点及最小抵抗线方向夹角h、炸药爆速i共9个影响因素为输入因子，以爆破振动峰值速度y为输出因子。参考相关研究，并通过多次试验确定的较优遗传参数，见表2。适应度函数采用相对误差适应度函数(式(3))。其中Q为取开方运算；E为以自然对数e为底的幂函数运算；A为取绝对值。据基因表达式编程思路，本文用Java语言编程，利用MyEclipse软件平台运算，建立爆破振动峰值速度预测模型。

2.2GEP预测

按GEP运算步骤，选择合适的函数符、终止符对种群初始化随机产生一个种群，对染色体进行解码计算适应度值；按程序中输入的遗传参数对染色体进行选择、复制、变异、插串、根插串、基因重组、单点重组、两点重组等遗传操作产生新个体，形成子代种群；通过赌盘方式选择适应度高的个体重复遗传操作。对表1归一化数据训练后，模型在迭代到68181代时达到历史训练的最佳代数，最大适应度值为1 348.847 430 615 532，输出最佳爆破峰值速度预测函数为

y=(((((f+c)e)(ic))×

(g(0.9015×0.9015)))+

((d(Abs[a]))(f(Exp[d]))))+(((0.5571b)

(1.4588f))(0.5571h))

(6)

由式(6)看出，GEP预测模型能较好发掘各因素对爆破峰值速度影响，并将其表示在预测公式中。通过LaTex软件输出表达式树见图3。

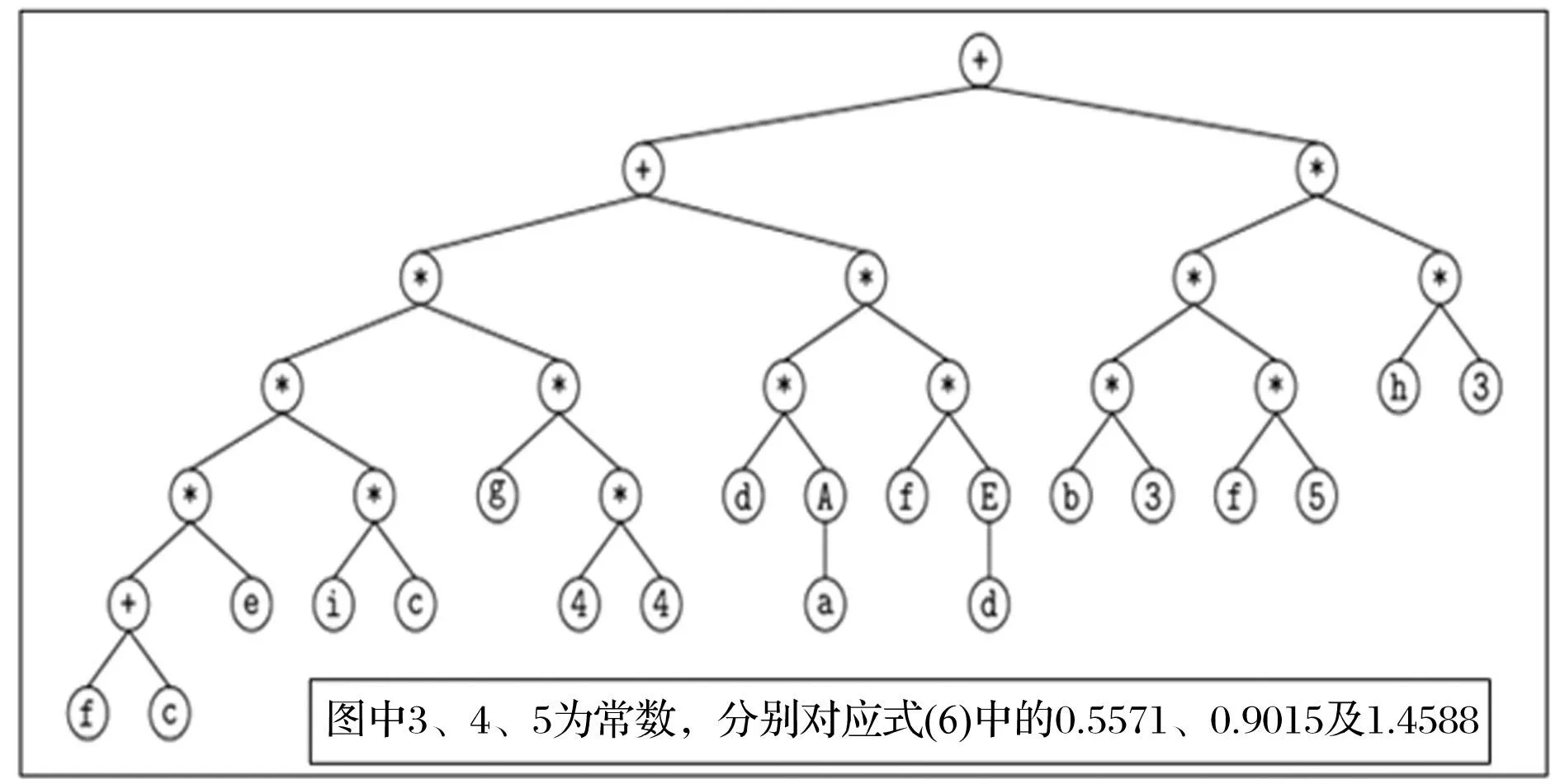
图3　表达式树 Fig.3 The expression trees

采用上文预测公式对后7组数据进行预测，得到最大预测相对误差为14.1%，最小预测相对误差为3.5%，误差已达较理想预测水平，见表3。

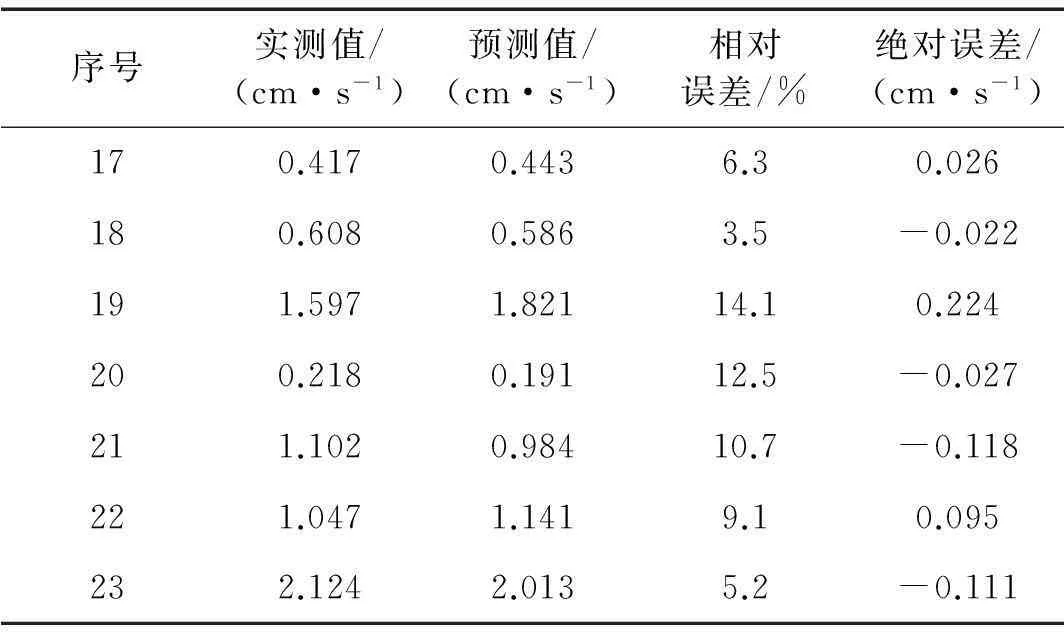
表3　预测结果

3预测效果分析

将GEP预测结果与文献[15]中模糊神经网络及萨道夫斯基公式预测结果进行对比，将爆破峰值速度实测值与GEP、模糊神经网络、萨道夫斯基公式预测值显示为结果序列曲线[17]，见图4。由图4看出，四者数据走势相符，但由于萨道夫斯基公式只考虑最大段药量与爆心距两个因素，使其预测结果偏离实测值较大。模糊神经网络与GEP算法预测效果均较好，但GEP算法精度更高、与实测值拟合性更好；模糊神经网络在训练过程中所用训练样本多达93组，而GEP算法仅用16组，说明GEP算法在爆破峰值速度预测中具有所需样本数量少、预测精度高等优点。

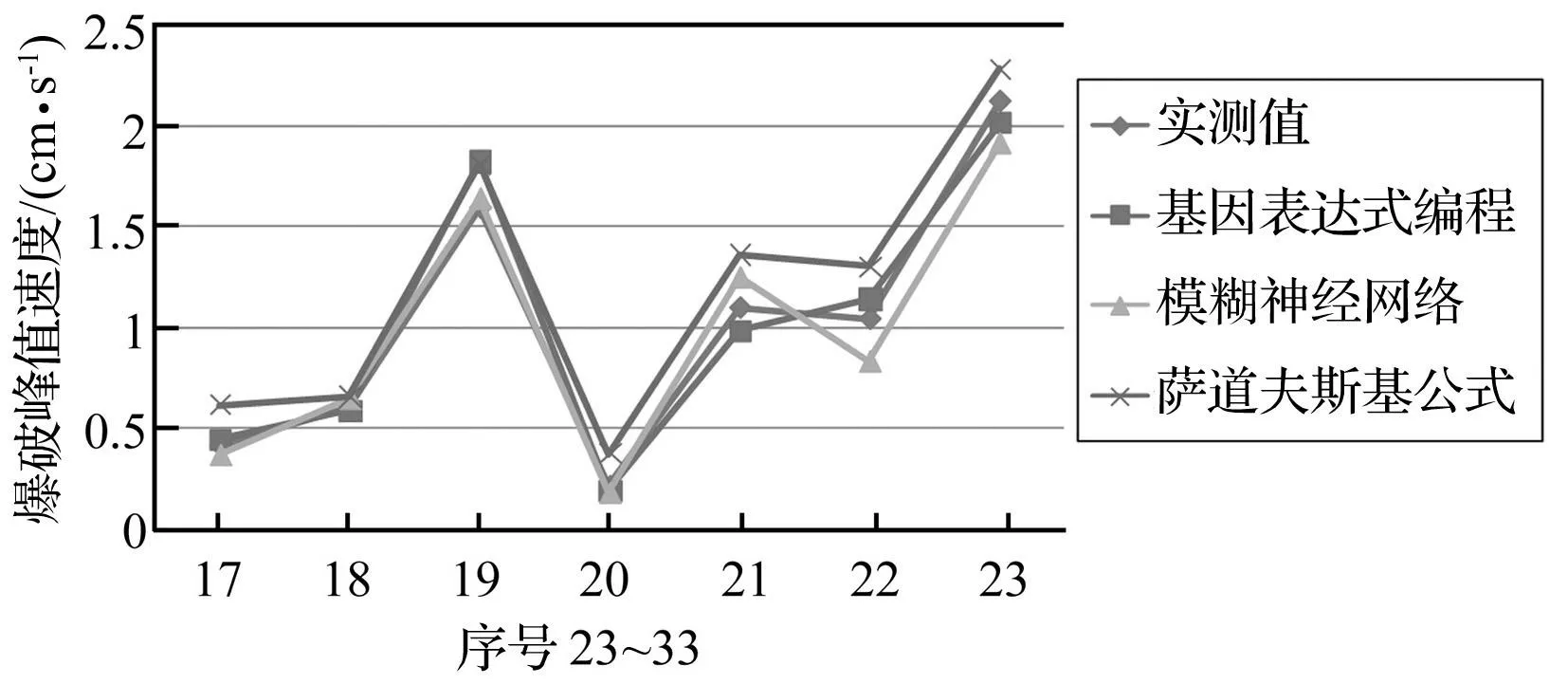
图4　峰值速度序列曲线 Fig.4 The sequence curves of peak speed

三种方法预测结果与实测值对比见表4。从表4可得，GEP模型预测结果与实测值的平均相对误差为8.8%，模糊神经网络预测结果与实测值平均相对误差为11.3%，萨道夫斯基公式的预测值与实测值平均相对误差为27.9%。显然，GEP模型预测结果更精确，与实测值拟合度更好。

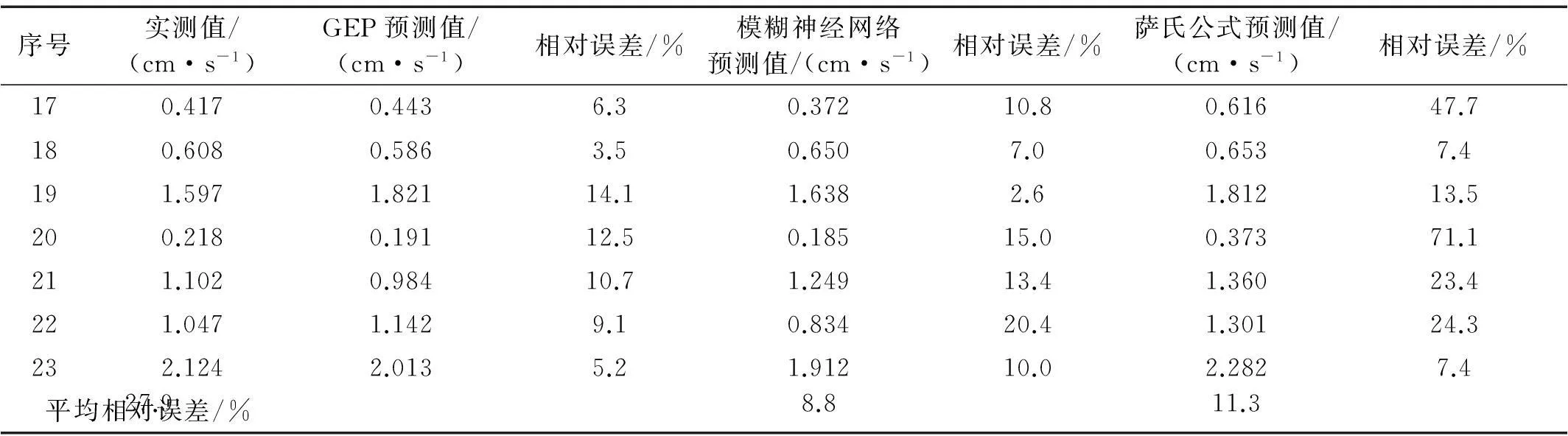
表4　预测结果与实测值对比

4结论

(1)GEP高效的遗传算子及有指导性的全局搜索寻优方式使之具备较强的非线性空间全局搜索能力，可较好处理爆破振动作用机理的复杂性及难描述性。通过对铜录山露天台阶爆破所建振动峰值速度预测模型计算研究表明，GEP能较全面发掘各因素间关系，输出预测公式、预测精度较好，较仅考虑最大段药量和爆心距的萨道夫斯基公式更科学。对露天爆破的指导作用更全面。

(2)通过爆破振动峰值速度实测值与GEP、模糊神经网络预测值对比表明，GEP模型预测与实测值平均相对误差仅8.8%，较模糊神经网络(平均相对误差11.3%)预测结果更精确；且GEP所用训练样本(仅16组)较模糊神经网络(93组)减少很多，可简化预测工作量。GEP用于爆破峰值速度预测可靠、科学。

参考文献

[1]史秀志,林大能,陈寿如. 基于粗糙集模糊神经网络的爆破振动危害预测[J].爆炸与冲击,2009, 29 (4): 401-407.

SHI Xiu-zhi, LIN Da-neng, CHEN Shou-ru. Blasting vibration induced damage prediction by rough set based fuzzy-neural network[J]. Explosion and Shock Waves, 2009, 29(4): 401-407.

[2]唐海,石永强,李海波,等. 基于神经网络的爆破振动速度峰值预报[J].岩石力学与工程学报,2007, 26(增1):3533-3539.

TANG Hai, SHI Yong-qiang, LI Hai-bo, et al. Prediction of peak particle velocity of blasting vibration by neural network [J].Rock mechanics and Engineering, 2007, 26(S1):3533-3539.

[3]方向,陆凡东,高振儒,等. 中深孔爆破振动加速度峰值的遗传BP网络预测[J]. 解放军理工大学学报(自然科学版)，2010, 11(3):312-315.

FANG Xiang, LU Fan-dong, GAO Zhen-ru, et al. A BP neural network model for forecasting of blasting vibration acceleration peak value from deep hole blasting[J].Journal of PLA university of science and technology: Natural Science Edition , 2010, 11(3):312-315.

[4]李菁,马彦琳,梁晓群. 基于基因表达式编程的电力消费预测模型-武汉市的实证[J]. 统计研究,2008, 25(4): 45-49.

LI Jing, MA Yan-lin, LIANG Xiao-qun. Prediction of Wuhan’ power consumption by gene expression programming[J]. Statistical Research, 2008, 25 (4): 45-49.

[5]杨晶,胡珉,吴耿峰. 基因表达式编程算法的改进及其应用研究[J]. 计算机工程与应用,2007, 43(6): 240-243.

YANG Jing, HU Min, WU Geng-feng. Improvement and application of gene expression programming[J]. Computer Engineering and Applications, 2007, 43(6): 240-243.

[6]刘桂琴. GEP在演化建模中的应用[D].武汉：华中师范大学,2009: 9-12.

[7]袁晖,元昌安,覃晓,等. 基于GEP自动聚类算法的视频关键帧提取方法[J].广西师范学院(自然科学版),2013,30(1): 98-101.

YUAN Hui, YUAN Chang-an, QIN Xiao, et al. A method of video key frame extraction based on GEP automatic clustering algorithm[J]. Journal of Guangxi Teachers Education University(Natural Science Edition), 2013, 30 (1): 98-101.

[8]王超,赵延军,董卓. GEP算法在变压器故障诊断中的应用研究[J].技术应用，2012, 60(3): 60-71.

WANG Chao, ZHAO Yan-jun, DONG Zhuo. Research on application of GEP algorithm in transformer fault diagnosis [J]. Journal of Communicate Technology, 2012, 60(3): 60-71.

[9]杜冬，麦海波. 基于GEP的四维飞行轨迹预测模型[J].四川大学学报(自然科学版),2013, 50(4): 749-752.

DU Dong, MAI Hai-bo. 4-D trajectory prediction model based on GEP[J]. Journal of Sichuan University(Natural Science Edition), 2013, 50(4): 749-752.

[10]孟艳,赵洪波,茹忠亮,等. GEP在桁架结构优化中的应用[J].工程力学,2013, 30(1): 237-241.

MENG Yan, ZHAO Hong-bo, RU Zhong-liang, et al. The application of GEP in truss structure optimization[J]. Engineering Mechanics, 2013, 30(1): 237-241.

[11]古玲岚. 基于GEP-RBF的协同过滤数据稀疏性问题研究[J].计算机与数字工程,2013, 9: 1432-1436.

GU Ling-lan. Data sparse issue of collaborative filtering algorithm based on GEP-RBF[J]. Computer and Digital Engineering, 2013, 9: 1432-1436.

[12]刘萌伟,黎夏,刘涛. 基于基因表达式编程的人口预测模型[J]. 中山大学学报(自然科学版),2010, 49(6): 116-120.

LIU Meng-wei, LI Xia, LIU Tao. A gene expression programming algorithm for population prediction problems [J]. Journal of Sun Yatsen University(Natural Science Edition), 2010, 49(6): 116-120.

[13]陈毅,杨一洋. 基于基因表达式编程的大坝位移强度聚类分析研究[J]. 测绘与空间地理信息,2013, 36(9): 33-36.

CHEN Yi, YANG Yi-yang. Study on clister analysis of dam deformation displacement intensity based on gene expression programming algorithm[J]. Geomatics and Spatial Information Technology,2013, 36(9): 33-36.

[14]刘传立,刘小生,李妍妍. 基于GEP的金属矿尾矿坝变形预测模型研究[J]. 有色金属科学与工程，2013, 6: 63-68.

LIU Chuan-li, LIU Xiao-sheng, LI Yan-yan. Research ondeformation prediction model of metal mine tailings dam based on GEP[J]. Nonferrous Metals Science and Engineering, 2013, 6: 63-68.

[15]史秀志. 爆破振动信号时频分析与爆破振动特征参量和危害预测研究[D].长沙：中南大学，2007: 93-115.

[16]刘博,史秀志,黄宣东,等. 基于拟牛顿法的QN-BP预测爆破振动峰值速度[J].中国有色金属学报,2013,23(5): 1428-1433.

LIU Bo, SHI Xiu-zhi, HUANG Xuan-dong, et al. Prediction of peak particle velocity of blasting vibration by QN-BP based on Quasi-Newton method [J]. The Chinese Journal of Nonferrous Metals, 2013, 23(5): 1428-1433.

[17]Shi Xiu-zhi, Zhou Jian, Wu Bang-biao, et al. Support vector machines approach to mean particle size of rock fragmentation due to bench blasting prediction[J]. Transactions of Nonferrous Metals society of China, 2012, 22(2): 432-441.