改进决策的带异常样本1－SVM算法及应用

第一作者王涛男，博士生，副教授，1977年生

通信作者李艾华男，博士，教授，1966年生

改进决策的带异常样本1-SVM算法及应用

王涛，李艾华，王旭平，蔡艳平，张敏龙(第二炮兵工程大学机电工程系， 西安710025)

摘要：针对正常类样本多、异常类样本缺乏问题，基于异常样本加入能提高分类能力及分类精度考虑，提出改进决策的带异常样本1-SVM算法，并用于机械设备异常状态检测。用两类样本同时训练1-SVM模型可改善1-SVM算法对异常样本的描述能力；通过调整决策边界提高1-SVM算法的分类精度。柴油机气阀机构故障检测实验结果表明，该算法对正常类及故障类样本的识别率均高于标准1-SVM算法及带异常样本的1-SVM算法。

关键词：一类支持向量机；异常样本；改进决策；故障检测

基金项目：国家自然科学基金青年科学

收稿日期：2013-12-19修改稿收到日期：2015-05-10

中图分类号:TH165.3;TN911.7文献标志码：A

An improved decision-making 1-SVM algorithm with abnormal samples and its application

WANGTao,LIAi-hua,WANGXu-ping,CAIYan-ping,ZHANGMin-long(Dept. of Mechanical and Electronic Engineering, The Second Artillery Engineering University, Xi’an 710025, China)

Abstract:Aiming at normal samples abundance and abnormal samples deficiency, as adding abnormal samples could improve classification ability and classification accuracy, an improved decision-making 1-SVM algorithm with abnormal samples was put forward and applied in abnormal condition detection of mechanical equipments. On the one hand, the 1-SVM model was trained with two kinds of samples to improve the description ability of the 1-SVM algorithm for abnormal samples. On the other hand, the decision boundary was adjusted to improve the classification accuracy of the 1-SVM algorithm. The improved 1-SVM algorithm was applied in fault detection of diesel engin valve train. The experimental results showed that recognition rate of the improved algorithm for normal class and fault class samples is higher than that of the standard 1-SVM algorithm and the 1-SVM algorithm only with abnormal samples.

Key words:one-class support vector machine (1-SVM); abnormal samples; improved decision-making; fault detection

由于一类支持向量机(One-Class Support Vector Machine，OC-SVM)在正常状态数据样本而无需故障样本情况下即可建立单值分类器，区分机器运行状态，且具有鲁棒性强、可有效处理小样本数据等优点，已被用于滚动轴承、转子、齿轮箱等机械设备故障诊断[1-3]。传统OC-SVM算法的训练样本不含非目标样本，但若能获得非目标样本并加入OC-SVM训练模型，则会提高分类能力及准确性[4-5]。在机械故障诊断中，故障样本较难获得，或需较大代价才能获得。若已获取设备某类故障数据样本对其弃之不用，则会造成较大浪费。基于此，本文提出一种改进决策的带异常样本OC-SVM算法。可用两类样本同时训练OC-SVM模型以改善OC-SVM算法对非目标样本的描述能力；也可通过调整决策边界提高OC-SVM算法的分类精度。

用于异常检测的OC-SVM方法有两种，即超平面模型[6]亦称1-SVM及超球体模型[7]亦称支持向量域描述(Support Vector Domain Description，SVDD)。选高斯核函数时，对相同目标样本1-SVM及SVDD支持向量机相同。作为核方法在一类问题中的两个分支，两种方法从不同角度寻找目标类样本的特征分布，1-SVM与标准SVM的机理更相近，而SVDD的几何意义更明确。由定性角度，SVDD的惩罚系数C值含义明确，即C值大小与超球体包围的目标样本个数呈正比关系。由定量角度，C值本身无确切意义，因此C值设置较困难。在某些数据集实验中，SVDD计算的超球体范围过大，降低异常点检测率[8]。与SVDD相比，1-SVM中参数v表示对目标样本误识率上限，同时也是支持向量占目标样本比例的下限，定量意义明确，在数学形式上采用1-SVM算法有利于参数设置。因此，本文主要研究1-SVM算法的改进及在机械设备异常状态检测中的应用。

1带异常样本的1-SVM算法

在算法推导中，用i,j作为正常样本索引，用l,k作为异常样本索引；分别用m，n表示正常、异常样本数量；设正常样本类别标记y为+1，异常样本类别标记y为-1。与标准1-SVM类似[9]，训练样本中含异常样本1-SVM算法的优化目标函数为

(1)

式中：ξi，ξl分别为对正常、异常样本错分的松弛变量。

式(1)对应的Lagrange函数为

(2)

式中：αi，αl，βi，βl为Lagrange乘子。

由函数极值条件知

(3)

从而可得

(4)

将式(4)各项代入式(2)，得

(5)

(6)

2带异常样本的1-SVM决策边界调整

1-SVM算法与传统有监督SVM算法的最大区别在于引入参数v。将1-SVM用于分类时受参数v影响较大。而v∈(0,1]，因此无论训练数据中是否包含异常样本，总有一定比例数据被判为异常点，使1-SVM的分类精度低于传统有监督的SVM。

由式(6)知，带异常样本的1-SVM决策函数可写为

(7)

若f(x)≤0，则待测样本为正常点；若f(x)>0，则待测样本为异常点。对机械设备异常状态检测而言，接受异常点(漏检)较拒绝正常数据(虚警)更糟糕，发生“漏检”时会严重危及设备运行安全，造成更大损失。由于特征空间中1-SVM的决策曲线(面)为以原点为中心的超球面，阈值为超球面半径b，为b乘一个系数可方便调整决策边界大小。因此，本文由算法生成决策边界入手引入决策边界调整系数ρ，对式(7)的判决函数f(x)进行改进。改进后决策函数为

(8)

当ρ<1时决策边界变大，判为异常点比例减小；当ρ>1时决策边界变小，判为异常点比例增大；当ρ=1时即为原1-SVM生成的决策边界。ρ的取值可据不同应用场合及据两类误判造成损失的不同程度确定。机械设备异常状态检测时接受异常点(漏检)较拒绝正常点(虚警)更不利，“漏检”会严重危及设备的运行安全，损失会更大。因此，此时建议选ρ<1，以增强对异常状态(样本)的敏感性。ρ值不能过小，过小会增大虚警率。据实验验证发现，ρ取0.8～0.9之间时效果较好且结果相差不大。而ρ的取值与数据集有关，数据集不同ρ取值范围会变化。

3应用实例

3.1实验装置及样本获取

以6135G柴油机为实验对象，将柴油机第2缸气门机构间隙设成多种不同组合状态模拟进、排气门多种间隙异常故障，实验工况设置见表1。由表1看出，气门正常间隙值为0.30 mm，0.06 mm模拟气门间隙过小，0.50 mm模拟气门间隙过大。

实验中柴油机运行状态为空载，转速稳定在1 500 r/min时测量缸盖的振动信号，等时间采样，采样频率25 kHz。以第一缸压缩上止点为采样起始点对缸盖振动信号进行整周期截取，样本采集工况1为96个，工况2为97个，工况3为95个，工况4为98个，工况5为96个。

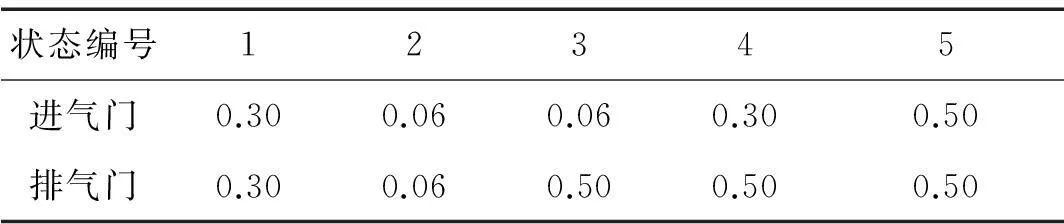
表1　实验工况设置(单位：mm)

通过对整循环缸盖振动信号Hilbert包络的幅值域特征参数、排气门关闭段振动信号的时序模型特征参数及缸盖振动信号小波包频带能量百分比特征参数进行分析，优选均值、均方根值、方根幅值、波形因数4个幅值域特征参数及第1、5、9、12、15个小波包频带能量百分比参数构成9维原始特征参数集[10]。

3.2诊断结果分析

为验证异常检测方法的可行性，构造两种训练数据集。第一种仅由32个工况1(正常状态)样本组成；第二种由32个工况1(正常状态)样本及22个工况2(故障)样本组成。测试数据集由22个工况1(正常状态)及2个工况2(故障工况)样本组成。针对数据集训练三种1-SVM模型，即标准1-SVM模型、带异常样本1-SVM模型及改进决策的带异常样本1-SVM模型。各种模型参数设置见表2。

表2　三种1-SVM模型参数设置

单分类实验中，由于正常、异常样本数量不平衡，不宜用错误率作为评价标准。本文用针对类别不平衡问题可信度较高的评价标准，即ROC曲线、AUC、查准率(precision)、查全率(recal1)及F分值评价分类器性能[11]。ROC曲线体现出正类识别率与反类误识率间的平衡，如果一条ROC曲线在另一条曲线左上方，则前者对应分类器的性能较后者好。AUC值指ROC曲线下面积，位于0～1之间。有效分类器的AUC值应大于0.5，且AUC值越大对应的分类器性能越好。在不平衡学习及正常类查全率尽量高前提下，查准率及F分值越大分类器性能越优。

三种1-SVM算法在测试数据集上形成的ROC曲线见图1。由图1可知，本文所提改进算法的ROC曲线在标准1-SVM算法ROC曲线左上方，表明改进算法的性能优于标准算法；但从直观上看不出本文算法性能的优越性。

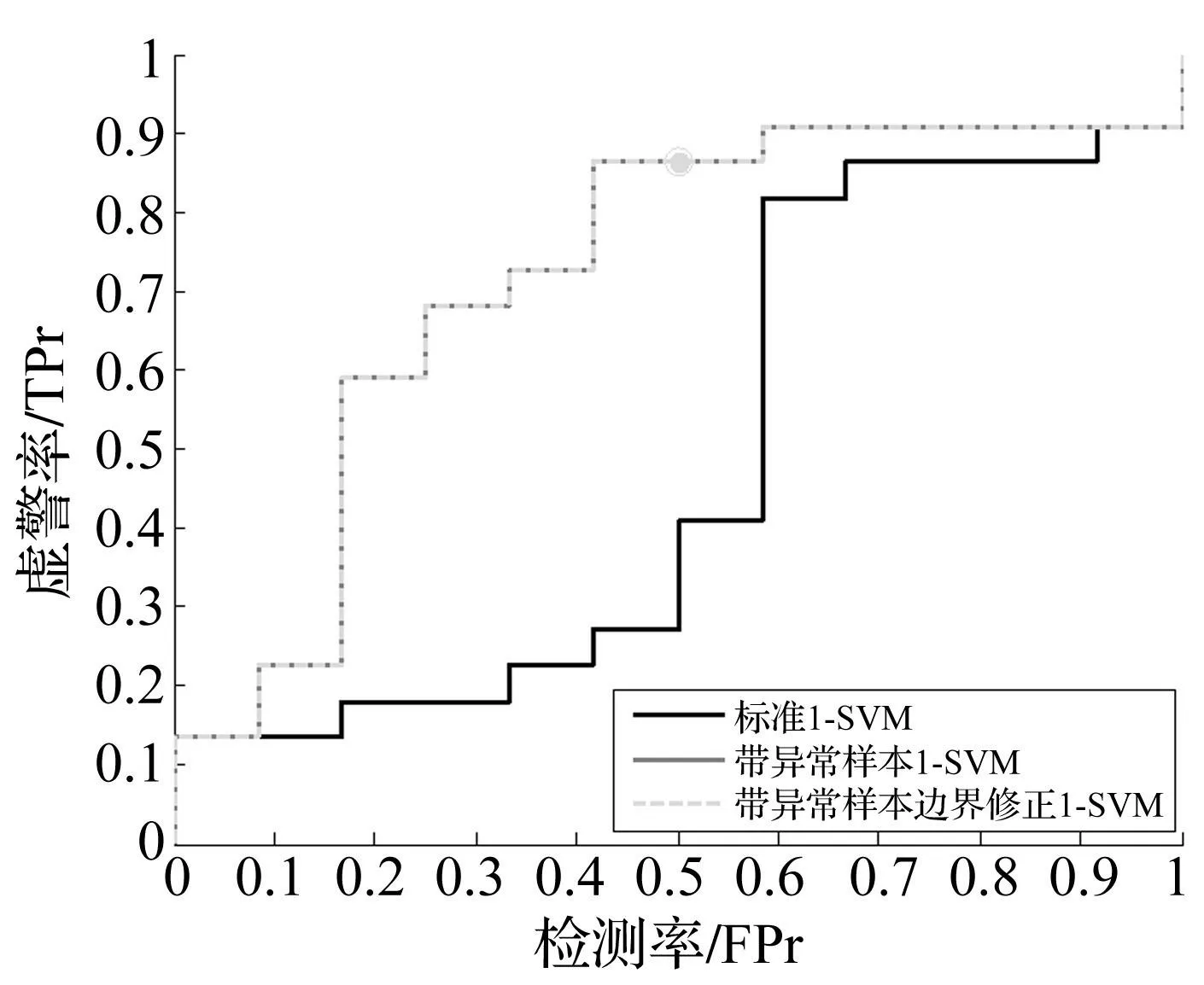
图1　三种1-SVM算法ROC曲线 Fig.1 ROC curves of three kinds of 1-SVM algorithm

为进一步从定量角度评估三种算法，分别对AUC值、查准率、查全率、准确率及F分值进行比较，见表3。由表3知，除查全率，改进决策、带异常样本1-SVM算法及带异常样本1-SVM算法其它指标均较标准1-SVM算法好。改进决策、带异常样本1-SVM算法在查准率、准确率及F分值上较带异常样本1-SVM算法好。综合各项模型评价指标，改进决策的带异常样本1-SVM算法性能最好。

表3　三种1-SVM算法性能比较

4结论

(1)鉴于传统1-SVM算法存在对训练样本分布的要求，本文基于异常样本加入能提高分类能力及分类精度考虑，提出改进决策的带异常样本1-SVM故障检测方法。该方法与标准1-SVM方法形式相同，并据两类误判造成损失的不同程度修改决策边界。

(2)为验证本文所提改进算法的有效性，将其用于柴油机气阀机构故障检测结果表明，较标准1-SVM算法及带异常样本1-SVM算法，改进决策的带异常样本1-SVM算法对正常及故障类样本均有较高识别率，且对样本数量依赖程度更小，学习及泛化能力更强。

参考文献

[1]李卫鹏,李凌均,孔维峰,等. 正交小波变换支持向量数据描述在故障诊断中的应用[J]. 机械科学与技术,2011, 30(3):466-470.

LI Wei-peng, LI Ling-jun, KONG Wei-feng, et al. Support vector data description in orthogonal wavelet transform for fault diagnosis[J]. Mechanical Science and Technology for Aerospace Engineering, 2011,30(3):466-470.

[2]陈斌,阎兆立,程晓斌. 基于SVDD和相对距离的设备故障程度预测[J]. 仪器仪表学报,2011,32(7):1558-1563.

CHEN Bin, YAN Zhao-li, CHENG Xiao-bin. Machinery fault trend prediction based on SVDD and relative distance[J]. Chinese Journal of Scientific Instrument, 2011,32(7):1558-1563.

[3]McBain J,Timusk M. Feature extraction for novelty detection as applied to fault detection in machinery[J]. Pattern Recognition Letters,2011(32):1054-1061.

[4]Tax D M J. One-class classification[D]. Delft: Delft University of Technica1, 2001.

[5]蒲晓丰，雷武虎，汤俊杰，等. 基于带野值的SVDD 的高光谱图像异常检测[J]. 光电工程,2010,37(12):83-87.

PU Xiao-feng, LEI Wu-hu, TANG Jun-jie,et al. Anomaly detection for hyperspectral image based on SVDD with negative examples[J]. Opto-Electronic Engineering, 2010,37(12):83-87.

[6]Scholkopf B, Platt J C, Shawe-Taylor J, Smola,et al. Estimating the support of a high-dimensional distribution [J]. Neural Comput,2001,13(7):1443-1471.

[7]Tax D M J, Duin R P W. Support vector data description [J]. Pattern Recognition Letters, 1999, 20(11/13): 1191-1199.

[8]Chandola V, Banerjee A, Kumar V. Anomaly detection:a survey[J]. ACM Computing Surveys,2009, 41(3):1-58.

[9]Schökopf B,Williamson R, Smola A, et al.Support vector method for novelty detection[C]. Advances in Neural Information Processing Systems 12[A]. Solla S A, Leen T K, Müller K R.MIT Press, 2000:582-588.

[10]王涛,李艾华,姚良,等. 采用多层核学习机的柴油机气阀机构故障诊断[J]. 振动、测试与诊断,2010, 30(4): 462-464.

WANG Tao, LI Ai-hua, YAO Liang, et al. Fault diagnosis of diesel valve train based on multi-layer kernel learning machine[J]. Journal of Vibration, Measurement & Diagnosis, 2010, 30(4):462-464.

[11]缪志敏,胡谷雨,丁力,等. SVDD在类别不平衡学习中的应用[J]. 应用科学学报,2008, 26(1):79-84.

MIAO Zhi-min, HU Gu-yu, DING Li,et al. Support vector date description implemented in class-imbalance learning[J]. Journal of Applied Sciences, 2008, 26(1): 79-84.