隔板贯通式全螺栓节点抗连续性倒塌性能数值模拟分析

第一作者秦希女，硕士生，1990年生

通信作者王伟男，博士，研究员，博士生导师,1977年生

邮箱: weiwang@tongji.edu.cn

隔板贯通式全螺栓节点抗连续性倒塌性能数值模拟分析

秦希2，王伟1,2(1.同济大学土木工程防灾国家重点实验室, 上海200092； 2.同济大学建筑工程系, 上海200092)

摘要：对不同构造的矩形钢管柱-H形钢梁隔板贯通式全螺栓连接节点进行数值模拟分析，考察窄盖板、较宽梯形盖板及较宽梯形盖板、梁下翼缘局部增大三种连接节点在连续性倒塌工况下的受力机理及破坏模式。结果表明，通过增大盖板尺寸，使初始断裂破坏位置外移至弯矩较小的外排螺栓处，可提高节点的承载能力。同时增大连接区域梁下翼缘宽度、盖板宽度，可使梁下翼缘连接处螺栓孔优先发生孔壁承压型破坏，延缓板件开裂，利于悬链线作用发展，大幅提高节点的承载能力。

关键词：连续性倒塌；隔板贯通式节点；螺栓连接

收稿日期：2014-03-03修改稿收到日期：2014-04-25

中图分类号:TU391文献标志码：A

Numerical simulation for progressive collapse behavior of through diaphragm bolted beam-column joints

QINXi2,WANGWei1,2(1. State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China；2. Department of Building Engineering, Tongji University, Shanghai 200092, China)

Abstract:Numerical simulation results of bolted I-beam-to-RHS column joints with through diaphragm against progressive collapse were presented. Three types of joints including narrow cover plate joints, wide cover plate joints and wide cover plate equipped with local strengthened bottom flange joints were investigated. Their load transfer mechanisms were clarified and their load-carrying capacities were evaluated. The results indicated that moving the initial position of fracture failure beyond the column by increasing the size of the cover plate can enhance the load-carrying capacity of the joints; at the same time, increasing the width of flange and cover plate in connection areas simultaneously may lead to bolt hole bearing failure, thus delaying the occurrence of cracking in plate is beneficial to the development of catenary action and obviously improving the load-carrying capacity of joints.

Key words:progressive collapse; through diaphragm joint; bolted connection

建筑结构因突发事件作用造成初始局部破坏可能导致相邻构件或部分结构的渐进失效，发生连续性倒塌现象。结构连续性倒塌研究历经发展，已从最初对结构体系的抗连续性倒塌分析、设计扩展至对节点或构件连接在抗结构连续性倒塌过程的性能研究[1]。建筑结构局部竖向承重构件失效后，剩余各部分的有效拉结可促成传力路径转变实现不平衡荷载重新分布为阻止结构连续性倒塌最有效方法。此时，梁柱连接节点性能对结构拉结作用的发挥具有重要影响。

将节点性能作为主要参数研究，考察剩余结构发挥悬链线效应能力。文献[2]对半刚性平端板连接梁柱节点进行两组试验，第一组比较螺栓直径与端板厚度之比及螺栓排列对节点延性影响，第二组比较钢材强度、端板与柱翼缘强弱关系对节点受力性能影响；Yang等[3-6]对7种不同构造节点(腹板连接、翼缘角钢连接、鳍板连接、TSWA连接、平端板连接、外伸端板连接)进行试验与数值模拟分析，并对比连接构造、角钢厚度等参数表明，梁柱节点子结构内力发展过程及破坏形态与节点刚度相关；Lee等[7]对有翼缘加劲板的栓焊节点进行平面拟静力加载试验，研究梁的跨高比对模型受力性态影响；Sadek等[8-11]对“三柱二梁”普通栓焊节点(WUF-B)及梁截面削弱型栓焊节点(RBS)进行平面内拟静力加载试验及数值模拟，考察其在中柱失效时不同破坏模式及承载能力；王伟等[12-14]选取含闭合截面柱-H形梁刚性节点的平面B-J-B子结构进行柱顶施加竖向集中荷载的静力试验研究，对比不同连接构造、不同梁跨高比的梁柱节点在连续性倒塌工况下性能。

以上研究表明，钢框架结构发生局部破坏后，由于节点承载力及变形能力限制，后续反应过程中节点性能往往起决定性作用，而节点的破坏模式及抗连续性倒塌性能主要依赖于节点的构造形式。本文利用ABAQUS有限元软件，对3个不同构造的矩形钢管柱-H形钢梁隔板贯通式盖板全螺栓连接节点进行数值模拟分析，考察在中柱失效情况下节点的受力机理、破坏模式及承载能力。

1节点构造设计

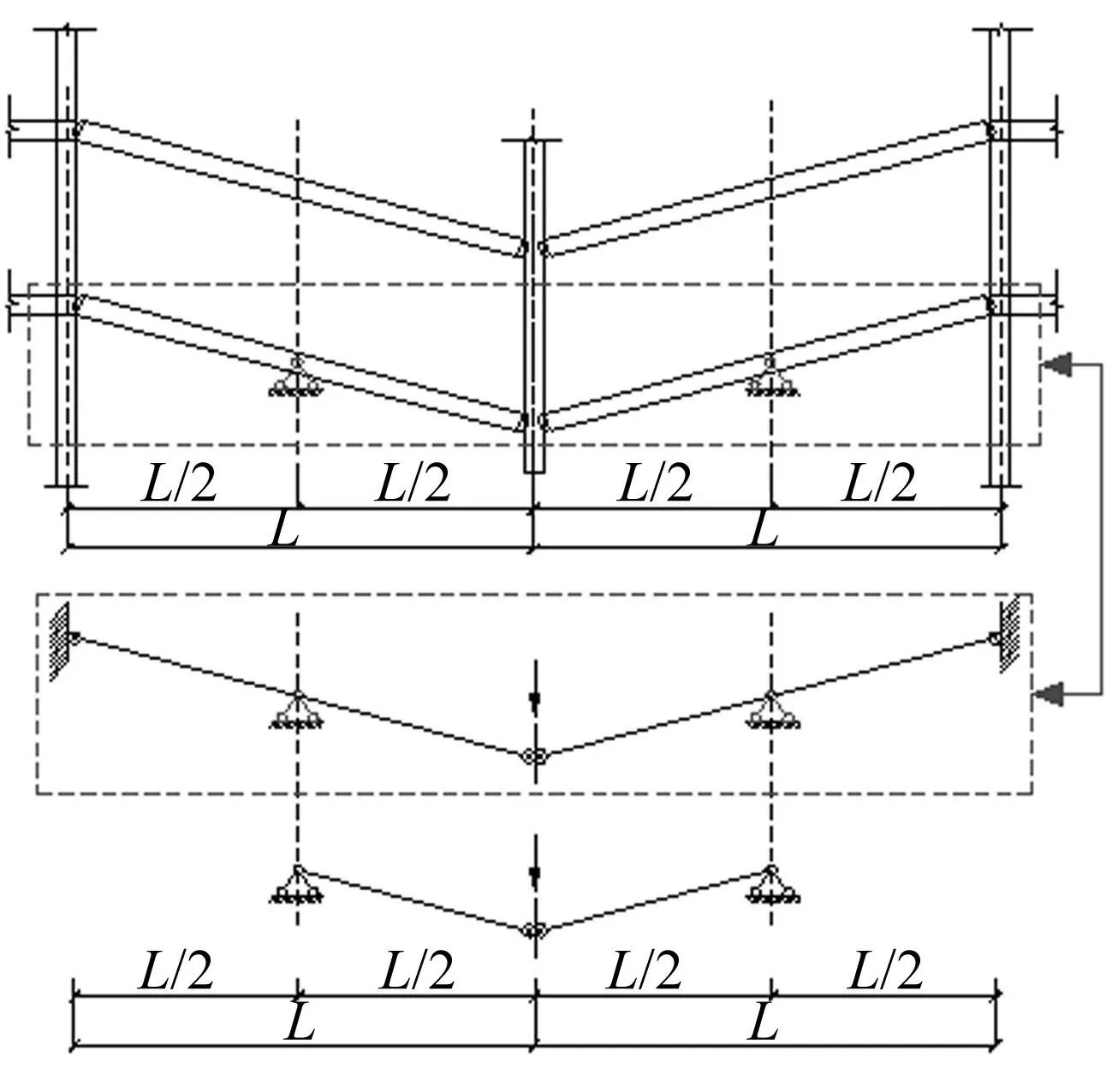
图1　梁柱节点原型 Fig.1 Prototype beam-column joint

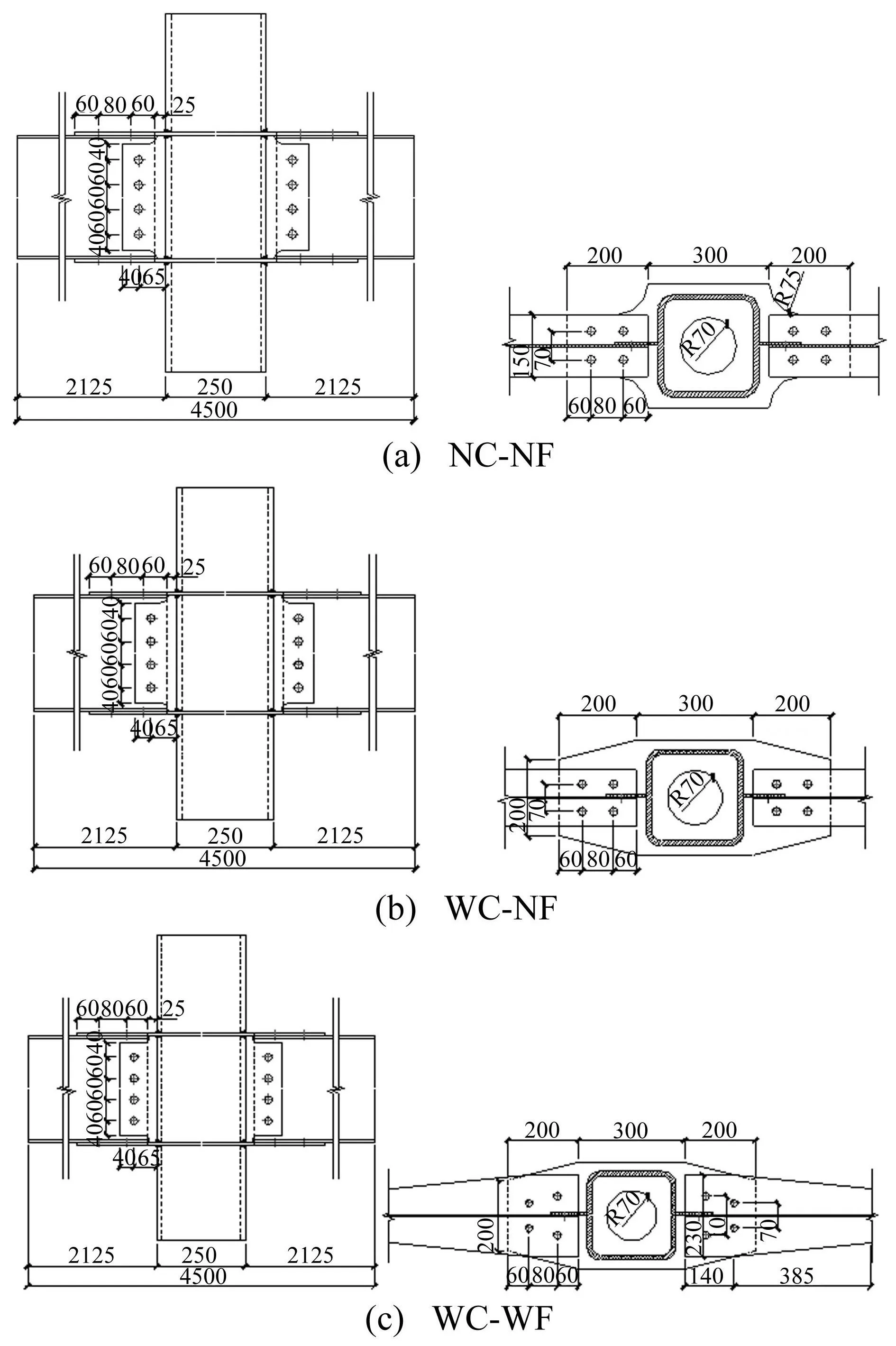
图2　模型构造详图(单位：mm) Fig.2 Model construction details(dimensions in mm)

备用荷载路径法指使主要承重构件失效后剩余结构通过冗余性能抵抗连续性倒塌的方法。文献[15-16]通过备用荷载路径法考察结构发生局部构件失效后性能，从而有效揭示出结构发生连续性倒塌过程及控制连续性倒塌发展的关键环节。典型工况见图1。框架内柱失效后，剩余结构通过荷载重分布抵抗原由失效柱承担的荷载。为简化分析，设反弯点位于梁跨中L/2处，在梁跨中插入铰，可得 “双半跨中柱节点”模型。

本文设计3个不同构造的“双半跨中柱”矩形钢管柱-H形钢梁隔板贯通式全螺栓连接节点。模型材料均用Q345钢，铰接点间跨度4 500 mm，柱高1 000 mm，柱截面尺寸□250×14，梁截面尺寸h100×150×6×8。方钢管柱与隔板(厚8 mm)采用开坡口全熔透焊接连接，梁腹板用4颗10.9级M20摩擦型高强螺栓通过剪切板(厚6 mm)与柱连接，螺栓孔直径22 mm。贯通的隔板作为盖板通过4颗10.9级M24摩擦型高强螺栓与梁翼缘连接，螺栓孔直径26 mm。连接处构件接触面喷砂后涂无机富锌漆，摩擦面抗滑移系数0.45。隔板中间开半径70 mm圆孔。其余参数见图2。

2数值模拟方法

利用ABAQUS软件建立有限元模型，材料弹性模量2.06×105MPa，泊松比0.3。材料应力-应变关系源于材性单调拉伸试验所得工程应力-应变曲线。

(1)

(2)

στ=σeng(1+εeng)

(3)

ετ=ln(1+εeng)

(4)

式中：Ffracture，Afracture分别为断裂时刻对应的荷载与试件的断后面积。

试验中材性试件断裂位置产生明显颈缩现象，据文献[8]方法，由式(1)、(2)计算断裂点断裂应力σfracture与断裂应变εfracture。有限元模型中材料属性应为其真实的应力-应变关系，因此需将工程应力-应变曲线由式(3)、式(4)换算成真实应力-应变曲线，将其由摘引伸计前的试验曲线线性延伸到由σfracture、εfracture确定的断裂点(σ=1 200 MPa)，并将以多折线拟合的真实应力-应变曲线输入有限元材性中。设置梁、剪切板、隔板及柱平直段的材料属性为M1，柱弯角段为M2，见表1。

大变形过程中，模型会出现材料断裂现象，并对承载力产生明显影响。“单元删除法”为常用模拟材料断裂方法，本文借助ABAQUS内置的延性金属损伤准则，通过定义材料的断裂应变、应力三轴性、应变率等参数实现单元删除。模型的梁、剪切板、隔板等部件均可能出现断裂现象，因此，亦为板件材料设置断裂属性。建立螺栓、梁、剪切板、隔板间接触关系时，由于板件接触处可能出现断裂现象，若采用“接触对”算法易造成计算结果不收敛，因此选“通用接触”算法定义部件的接触关系。设切向接触属性为“库伦摩擦”，摩擦系数取0.45，与摩擦面的抗滑移系数一致；设法向接触属性为“硬接触”。

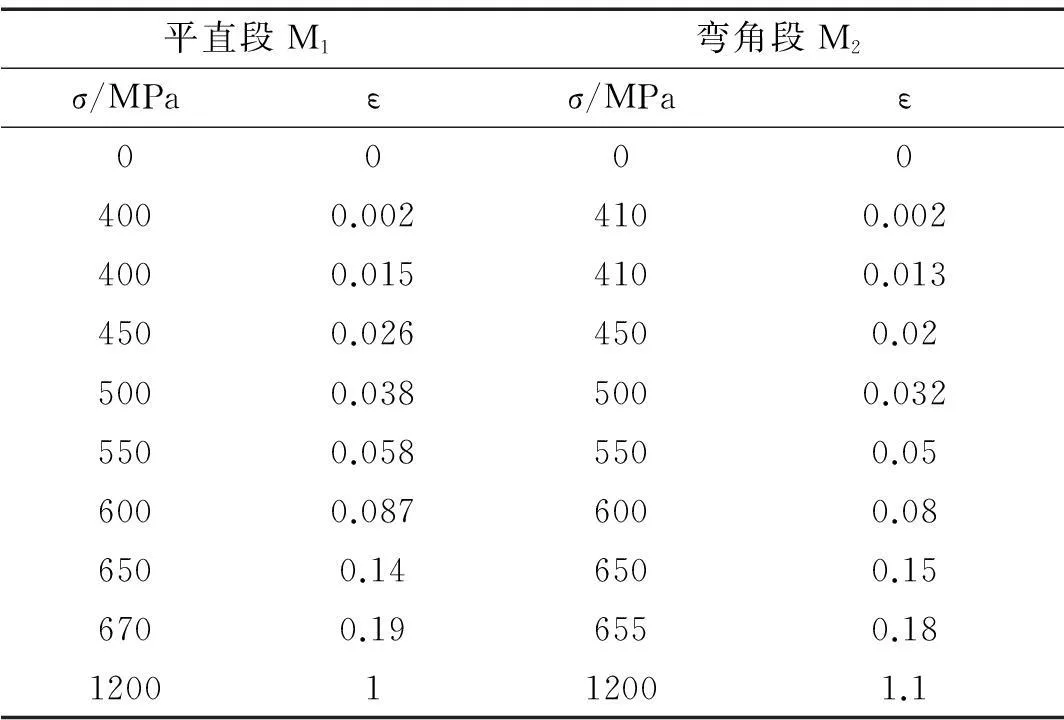
表1　材料应力-应变关系

有限元模型中存在的大变形、材料不连续及复杂接触问题易致刚度矩阵奇异，而用隐式积分算法则难以收敛。因此用显式动态分析克服接触对数量多、材料断裂模拟所致不收敛问题。分析步中设置合理的加载速率、较小增量步，以减小加载过程中产生的惯性力。柱顶竖向位移加载时，采用平滑的“smooth step”加载曲线，使接触能平稳建立。该措施可保证分析过程中的动能不超过内能的5%～10%(准静态分析)，认为此时分析结果与静态分析结果相近。

利用ABAQUS软件对3种节点形式据其真实尺寸建立有限元模型，所有部件均采用C3D8R实体单元，并对应力集中及断裂处划分1 mm的较密网格。模型WC-NF全局坐标、边界条件及网格划分见图3，其余模型类似。“双半跨中柱节点”模型两侧梁端为固定铰支座，柱顶与柱底仅发生竖向位移。因此，有限元模型中设梁端边界条件为铰接，铰支座可提供竖向反力及横向拉结力，柱顶、柱底设为Z向滑动约束，在柱顶实行Z向位移加载。

图3　网格划分及边界条件 Fig.3 FE modeling and boundary condition

选文献[13]中SI-WB试件为模拟对象，据数值模拟方法建立有限元模型，有限元分析与试验的柱顶竖向荷载-位移曲线及破坏对比见图 4、图5。由两图看出，有限元分析结果与试验结果存在一定差异，可能有限元模型所设材料应力-应变本构关系未考虑试件材料的各种缺陷所致，但有限元分析结果仍能反映梁柱子结构在竖向大变形下的主要受力特征。因此，数值模拟方法对节点的抗连续性倒塌性能模拟分析具有良好的适用性。

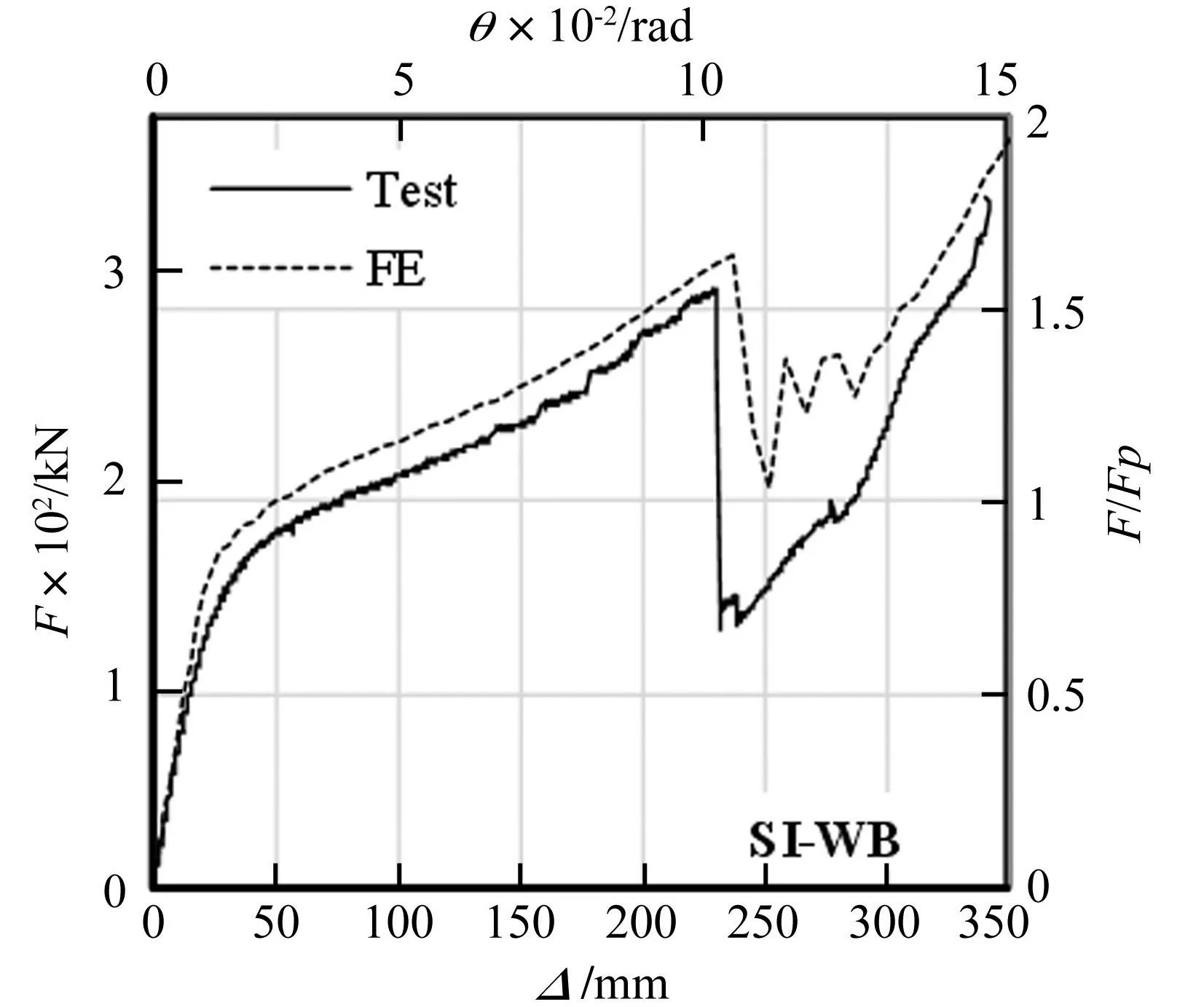
图4　SI-WB柱顶荷载位移曲线 Fig.4 Load-displacement curves of SI-WB

图5　SI-WB破坏现象 Fig.5 Failure mode of SI-WB

3数值模拟结果与讨论

3.1竖向荷载-位移曲线与破坏模式

数值模拟结果对比分析以NC-NF模型为基准，由于该模型梁端上下翼缘螺栓孔削弱了梁截面面积(图2)，因此，以偏离中轴线210 mm处截面作为该荷载工况下最不利截面，该截面达到全截面塑性受弯承载力(Mp=188 kN·m)时，对应的梁柱子结构柱顶荷载理论值为Fp=184 kN(Fp将用于荷载的无量纲化计算)。3模型中柱竖向荷载-位移曲线见图6，其中位移、荷载分别除以半跨长L/2(2 250 mm)及Fp获得θ(梁弦转角)以及F/Fp获得无量纲表述，曲线展示了模型在柱顶竖向位移逐渐增大过程中的受力全过程。各模型在梁弦转角θ达到0.2 rad时的破坏模式见图7。

由两图看出，NC-NF模型在初始阶段，竖向荷载随柱顶竖向位移线性增长，与WC-NF、WC-WF模型受力状态一致；柱顶竖向位移达到23 mm(θ=0.01 rad)时刚度明显降低，3模型的荷载-位移曲线出现分叉；柱顶竖向位移达到141 mm(A点，θ=0.063 rad)时梁下翼缘连接处盖板开裂，荷载由192 kN(1.04Fp)迅速下降89%；此后节点子结构依靠梁上翼缘及腹板处连接抵抗柱顶荷载，荷载逐渐回升并超过断裂前峰值, 剪切板螺栓孔由下至上逐次开裂；柱顶竖向位移达到428 mm(B点，θ=0.19 rad)时荷载达到最大值268 kN(1.46 Fp)并开始下降；柱顶竖向位移增大至459 mm(θ=0.2 rad)后开裂发展至上部盖板，荷载迅速下降，模型破坏丧失承载力。

WC-NF模型在初始阶段，竖向荷载随柱顶竖向位移线性增长；柱顶竖向位移达到23 mm(θ=0.01 rad)时刚度明显降低，与梁上翼缘连接的盖板局部明显屈曲；柱顶竖向位移达到206 mm(C点，θ=0.091 rad)时梁下翼缘在外排螺栓孔处断裂，荷载由291 kN(1.58 Fp)迅速下降47%；随柱顶竖向位移增大，破坏向上发展，梁腹板由下向上开裂，盖板的屈曲现象逐渐消失，荷载回升并超过断裂前峰值；柱顶竖向位移增大至397 mm(D点，θ=0.176 rad)时荷载达最大值348 kN(1.89Fp)，之后梁腹板裂缝向内延伸至螺栓孔，荷载迅速降低。WC-NF模型初始断裂破坏对应柱顶竖向位移、荷载较NC-NF模型分别提高36%、34%，后期荷载最大值高23%。

WC-WF模型在初始阶段，竖向荷载随位移线性增长；柱顶竖向位移达到26 mm(θ=0.012 rad)时刚度明显降低；之后荷载稳步上升，梁下翼缘与盖板连接处螺栓孔因承压破坏而不断伸长；柱顶竖向位移达到352 mm(θ=0.156 rad)时梁下翼缘外排螺栓孔开裂，荷载达最大值627 kN(3.41Fp)，之后开裂由下翼缘迅速扩展至梁腹板螺栓孔，荷载迅速降低。WC-NF模型发生初始断裂破坏对应的柱顶竖向位移、荷载较NC-NF 模型分别提高69%、63%，荷载最大值高57%，WC-WF模型柱顶荷载-位移曲线只有一个峰值。

加载过程中模型弯矩与轴力共同作用，梁下翼缘及盖板主要传递拉力，而连接二者的螺栓受剪力作用，梁下翼缘、盖板分别在内、外排螺栓处受力最大，模型破坏模式主要取决于各部件的承载力及受力大小，3模型均在最不利位置发生初始破坏：NC-NF模型用150 mm宽盖板，内排螺栓处内力较大而净截面面积较小，与梁下翼缘连接的盖板在此截面受拉开裂；WC-NF模型用较宽的梯形盖板，截面承载能力相应提高，使危险截面外移至梁净截面面积最小的外排螺栓处；WC-WF模型用较宽的梯形盖板，并局部增大梁下翼缘宽度，梁下翼缘外排螺栓处成为薄弱部位。

结果表明，NC-NF及WC-NF模型在梁下翼缘与盖板连接处失效后可通过剩余截面传力，使节点子结构承载力恢复，并超过前期荷载峰值。通过增大盖板尺寸，使初始断裂破坏位置外移，可提高模型的承载能力；同时增大盖板尺寸及连接区域梁下翼缘宽度，可显著提高模型承载能力。

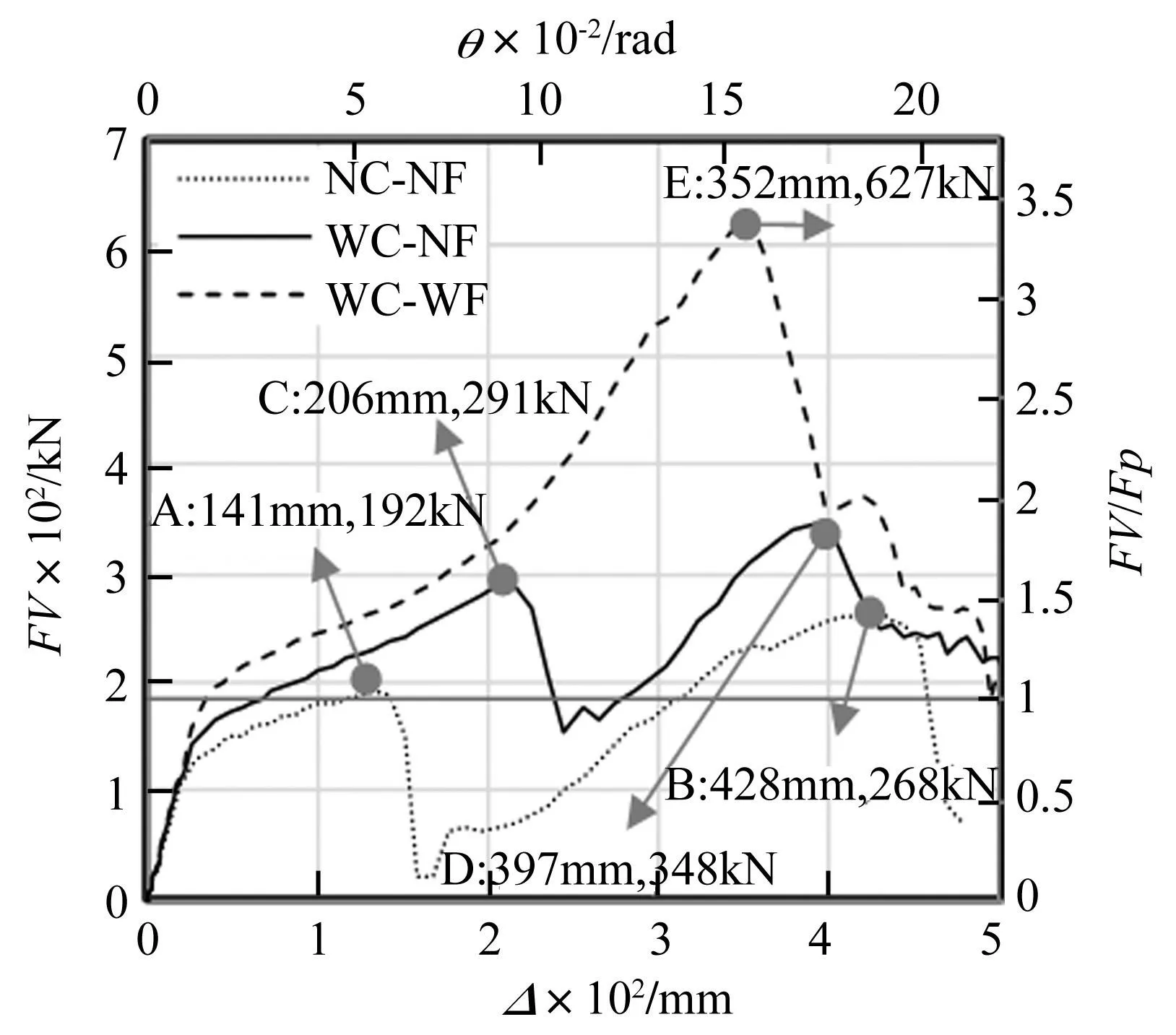
图6　柱顶竖向荷载-位移曲线 Fig.6 Vetical load-displacement curve

图7　破坏模式(θ=0.2 rad) Fig.7 Failure modes

3模型变形形态类似， WC-NF模型变形形态见图8，图中曲线展现了中柱竖向位移作用下模型变形全过程：柱顶竖向位移较小时形状呈二次抛物线，以弯曲变形为主；随柱顶竖向位移增大，铰支座与中柱间梁段逐渐呈直线，此时梁段以受轴向拉力为主，可见，竖向抗力机制已由抗弯作用转为悬链线作用。

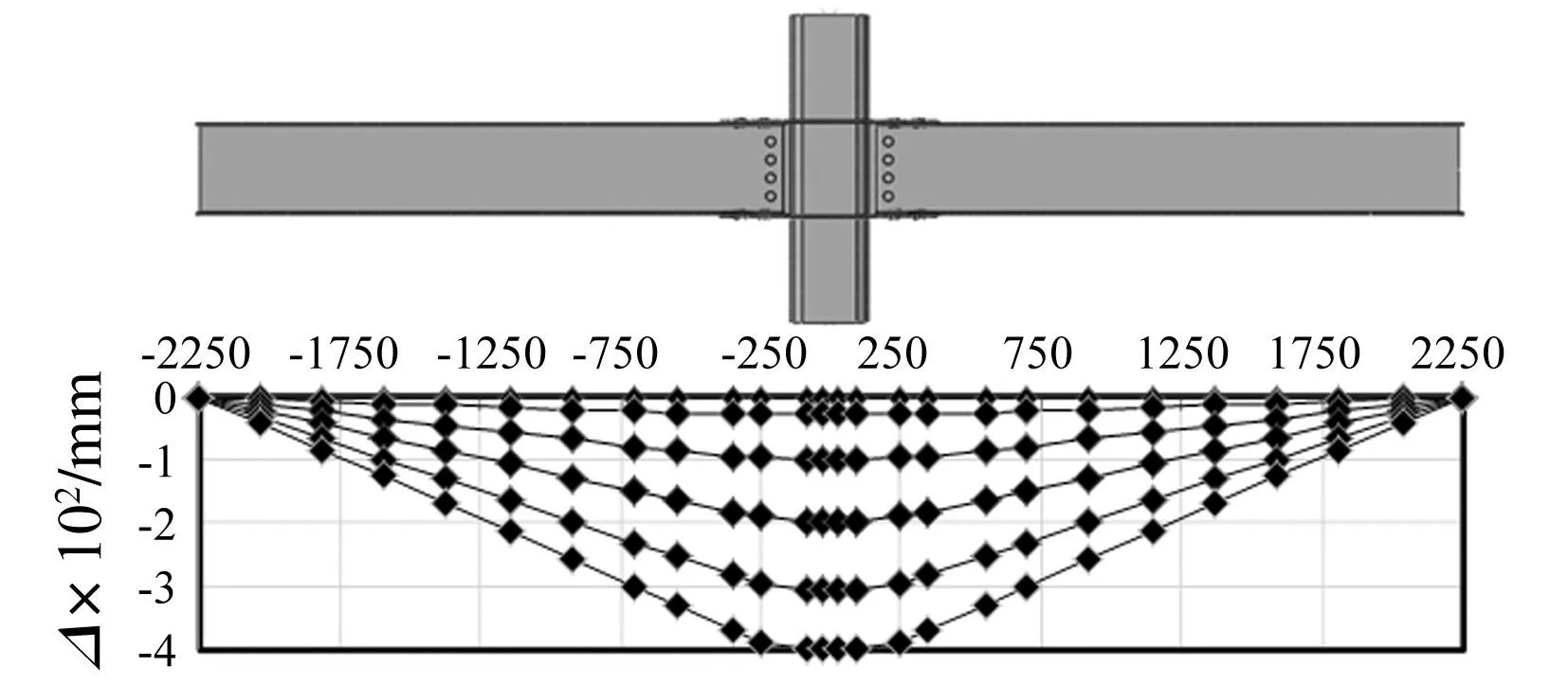
图8　模型WC-NF变形形态 Fig.8 Deflection profiles of WC-NF

3.2梁截面应力发展与分布

螺栓连接区域外侧梁截面(距中轴线350 mm)即截面1见图9。其中图9(b)为NC-NF、WC-NF模型截面，图9(c)为WC-WF模型截面。

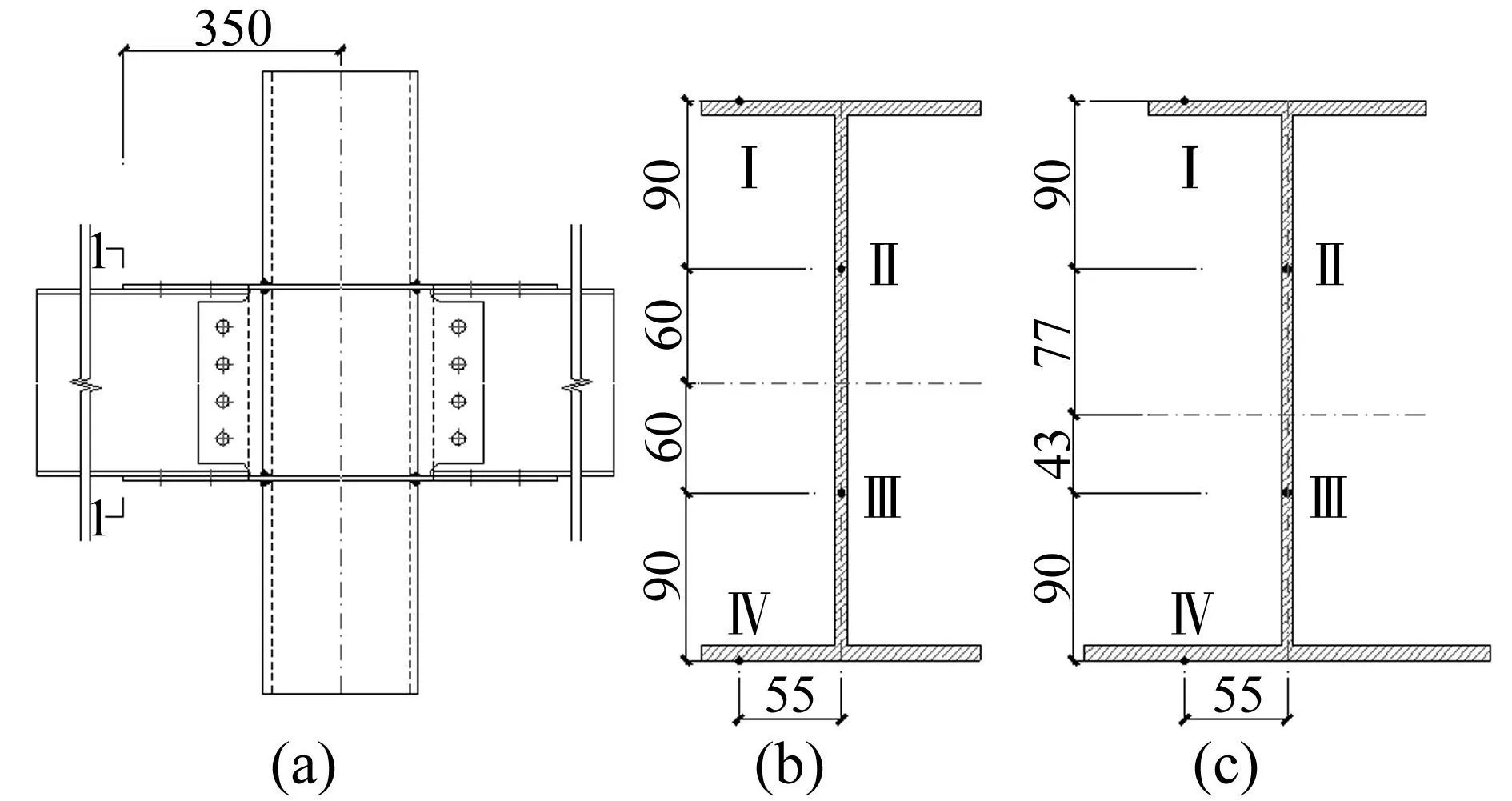
图9　截面1示意图 Fig.9 Schematic view of cross-section 1

各模型在该截面的应力随梁柱顶竖向位移发展曲线及对应不同弦转角的应力分布见图10(θ=0.01 rad、

θ=0.05 rad、θ=0.1 rad、θ=0.15 rad、θ=0.2 rad)。由图10看出，模型在初始受力阶段(0～0.01 rad)，梁上翼缘受压下翼缘受拉，中和轴与形心轴基本重合，截面拉压应力线性、对称发展，此阶段模型主要通过抗弯作用提供抗力。随柱顶竖向位移增大中和轴由形心轴向上偏移，截面受力由纯弯状态转为拉弯状态。梁下翼缘与盖板传力失效后，位于梁下翼缘的Ⅳ点拉应力迅速降低，位于腹板下部的Ⅲ点拉应力随梁下翼缘回缩也有所降低。变形较大时，分别位于梁上翼缘及腹板上部Ⅰ、Ⅱ点压应力随梁伸长不断减小，并逐渐转为拉应力，截面1转为受拉状态。

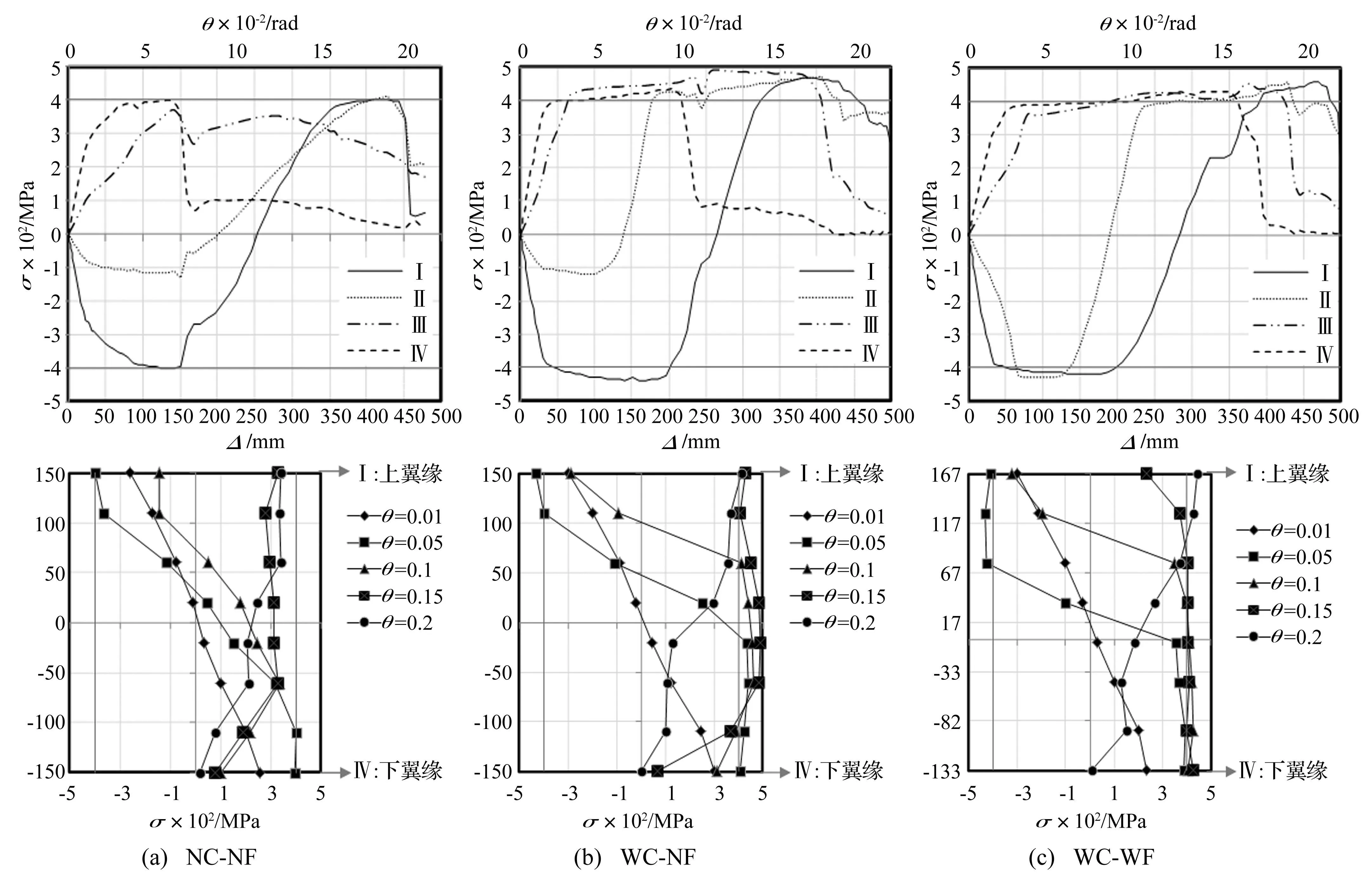
图10　截面1应力发展与分布 Fig.10 Stress development and distribution at cross-section 1

对比3模型可知，断裂前NC-NF模型只有梁翼缘能达屈服强度，WC-NF模型梁翼缘及腹板下方部分区域能达屈服强度，WC-WF模型只有位于形心轴上方的小部分腹板区域未达屈服强度。可见，断裂前WC-WF模型截面1应力值达较高水平，截面各点材料强度得到充分发挥，抗弯承载力最大。从梁翼缘(Ⅰ点、Ⅳ点)屈服到模型断裂，NC-NF模型柱只向下移动41 mm，WC-NF模型柱向下移动171 mm，WC-WF模型柱向下移动312 mm，说明WC-WF模型可在较大变形范围内保持截面完整性，有利于截面塑性发展。另外，NC-NF及WC-NF模型Ⅰ点压应力均因断裂而转为拉应力，而WC-WF模型Ⅰ点压应力在断裂发生前已转为拉应力。

3.3内力发展路径分析

3模型截面1的弯矩及轴力随柱顶竖向位移发展曲线见图11，其中Mp与Np分别为梁全截面塑性抗弯承载力及轴拉屈服承载力，分别取为188 kN·m及1 641 kN，用于弯矩及轴力的无量纲化。由图11看出，初始阶段(0～0.01 rad)截面1弯矩线性增长而轴力增长缓慢，截面以受弯矩作用为主；之后弯矩缓慢增长后基本维持不变，此时NC-NF及WC-NF模型弯矩值近似于0.82 Mp，WC-WF模型弯矩值约为1.15 Mp，轴力在此阶段呈稳定增长趋势。NC-NF及WC-NF模型发生局部断裂后(A点、C点)，承受拉力的梁下翼缘传力路径失效，截面主要依靠上部残余截面受拉提供抗力，由图10(a)(b)可知，截面拉应力呈上大下小分布形态，故其合力矩(即截面1弯矩)持续下降并转为负值，而轴力在有所降低后加速增长，并超过前峰值，在分别达到0.52Fp及0.7Fp后保持稳定；由图10(c)可知，WC-WF模型截面1随轴力迅速发展，梁上翼缘及上方腹板压应力逐渐转为拉应力，因此断裂前其弯矩值已开始缓慢下降，在梁下翼缘断裂后E点)迅速下降转为负值。断裂产生时截面1轴力达最大值1.0 Fp，但由于断裂迅速扩展至腹板螺栓孔，有效传力截面急剧减小，轴力下降后不再回升。

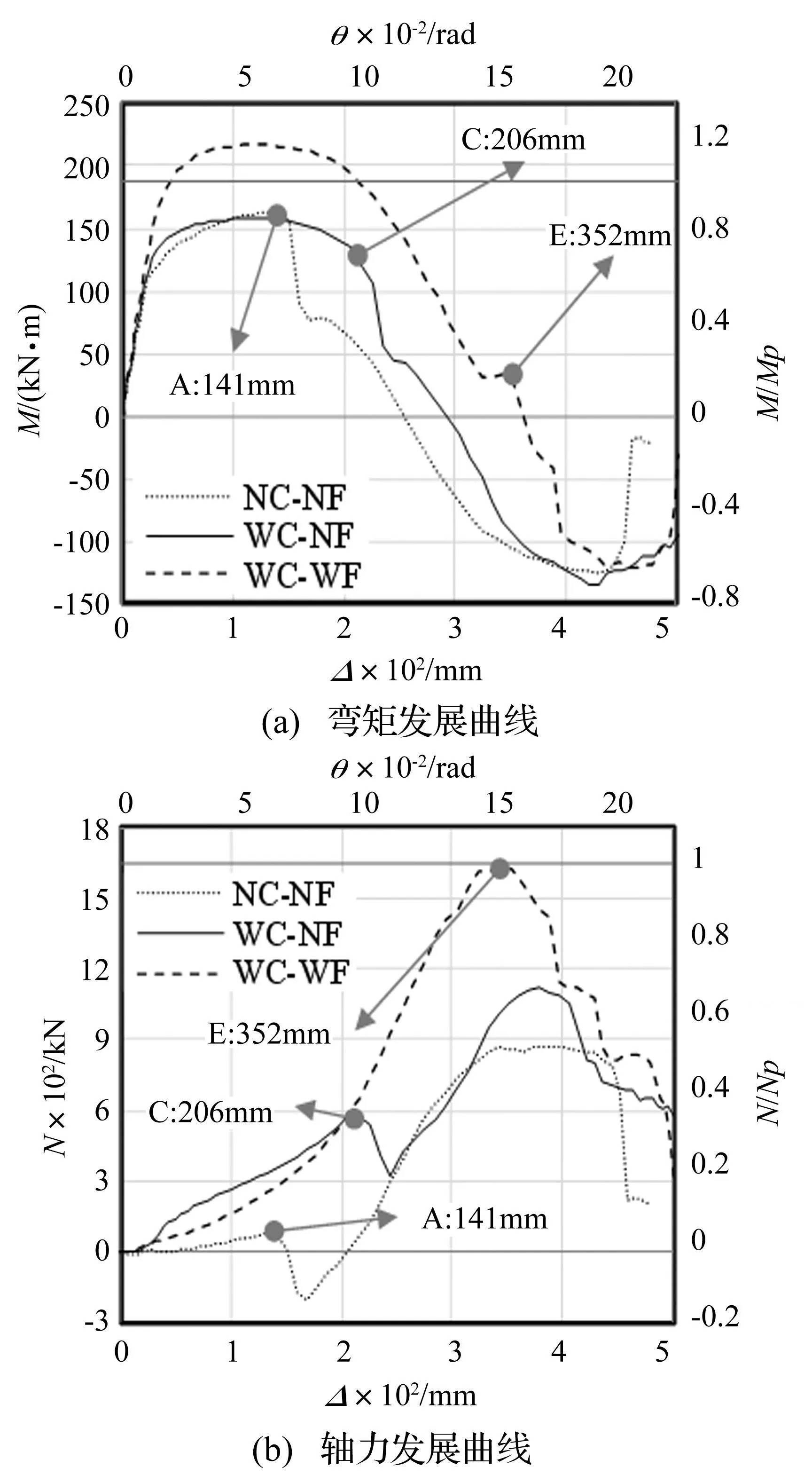
图11　截面1弯矩及轴力发展曲线 Fig.11 Bending moment and axial force development at cross section 1

对比3模型知，WC-WF模型截面1可发展更大的弯矩、轴力。弯矩最大值约为NC-NF及WC-NF模型的1.22倍。WC-WF模型在较大变形下发生断裂，此时截面1已由受弯为主状态转为受拉为主，基本达到全截面受拉屈服，截面承载力得到充分发挥。NC-NF及WC-NF模型截面1弯矩因断裂产而下降，抗弯承载力严重削弱，截面通过发展轴力提供抗力，但由于有效传力截面被削弱，轴力最大值远小于WC-WF模型， NC-NF及WC-NF模型截面过早断裂限制了截面内力的发展。

3.4竖向抗力机制分析

中柱失效后，梁柱节点提供的承载力可抵抗原由失效柱承担的重力荷载。如图12所示，节点中柱竖向荷载FV由截面轴力及剪力的竖向分量共同承担，其中，轴力竖向分量之和FC源于节点子结构悬链线作用，截面剪力竖向分量之和FF源于抗弯作用。本文提取铰支座处A、B截面轴力，并评估两种抗力机制提供的承载力大小，即

FC=NAsinθ+NBsinθ

(5)

FF=FV-FC

(6)

式中：FV为模型柱顶竖向荷载；FC为悬链线作用提供的竖向承载力；FF为抗弯作用提供的竖向承载力；NA，NB为铰支座处梁截面轴力。

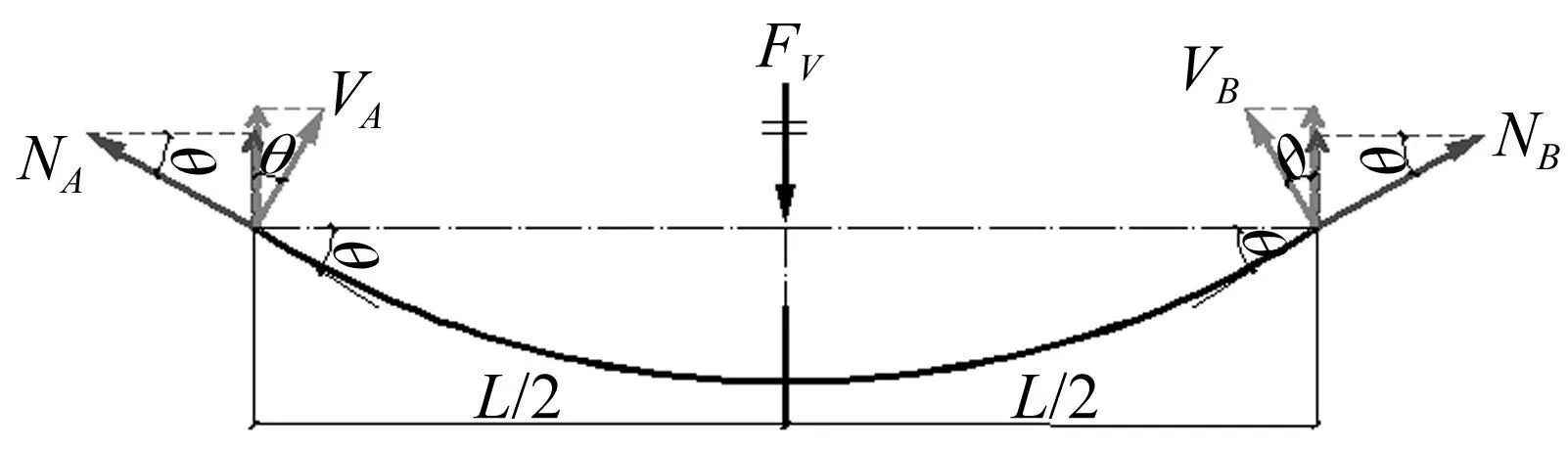
图12　节点子结构受力模型 Fig.12 Mechanical model of beam-to-column assembly

各模型弯矩作用及悬链线作用提供的竖向承载力随柱顶竖向位移发展曲线见图13，图中展示了随施加于柱顶竖向位移增大，主要抗力机制由抗弯作用逐渐转为悬链线作用全过程。与图10、图11对比知，抗弯作用FF发展与截面1弯矩发展一致；悬链线作用FC发挥由梁截面轴力与梁弦转角两因素决定。加载前期，梁弦转角值较小，FC发展滞后于截面1轴力发展；加载后期，梁弦转角增大，FC较轴力增长快，且在轴力维持不变时仍可增长。

NC-NF模型开裂较早(θ=0.063 rad)，因此开裂前，其竖向承载力几乎全由抗弯作用提供。WC-NF模型开裂前FC虽有所发展，但大部分抗力仍由FF提供。NC-NF与WC-NF模型开裂后(A点、C点)，FF大幅降低；随后FC迅速增长，抗力机制由抗弯作用向悬链线作用转化；随截面不断开裂， FF持续下降并转为负值，而FC仍可增长，除抵抗柱顶施加荷载外，需消解FF产生的负承载力，在柱顶竖向荷载分别达到428 mm(B点：0.19 rad)及397 mm(D点：0.176 rad)时，FC分别达最大值1.75Fp及2.12Fp。WC-WF模型开裂前FF已逐渐降低，而FC加速增长，抗力机制由抗弯作用向悬链线作用转化；开裂时(E点：0.156 rad)FC达最大值3.4Fp，之后FF与FC均降低。

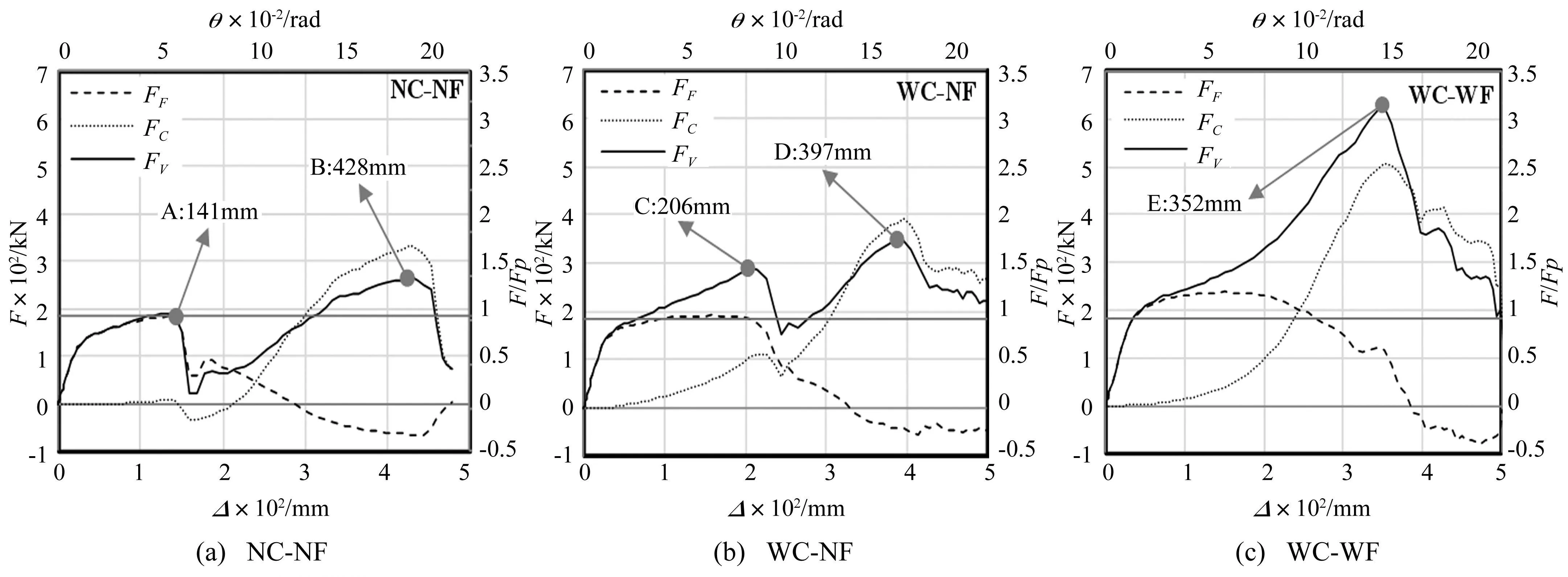
图13　弯矩作用及悬链线作用发展曲线 Fig.13 Resistance provided by flexural or catenary mechanism.

变形较大时模型抗力主要由悬链线作用提供。丧失承载力前，3模型均能达到较大变形(B点、D点、E点)，但较NC-NF及WC-NF模型，WC-WF模型可发展更大轴力，通过悬链线作用提供更大竖向承载力，可见，模型承载力不仅依赖于其最终变形能力，亦依赖于截面完整状态的变形能力。

3.5螺栓传力及螺栓孔变形分析

NC-NF、WC-NF及WC-WF三种不同构造的节点，在后续竖向大变形过程中利用悬索机制提供竖向抗力。模拟结果显示，盖板及梁下翼缘连接区域尺寸影响模型断裂时的变形大小，并使节点子结构承载能力产生分化。在此通过对断裂位置螺栓传力及螺栓孔变形形状分析，探究盖板及梁下翼缘构造影响。3模型断裂均从螺栓孔处开展，断裂位置螺栓孔均产生椭圆化变形，见图14。由图14看出，螺栓孔椭圆化由两种变形成分合成：①梁下翼缘与盖板在加载过程中传递拉力，在拉力作用下部件整体被拉长，螺栓孔被拉成椭圆形。若拉力持续增长，净截面面积最小截面将产生收

缩现象并发生断裂，即受拉破坏；②部件与螺栓间通过螺栓孔承担螺杆压力传力，螺杆挤压螺栓孔会使螺栓孔伸长，若变形较大，螺栓孔壁会开裂，即发生孔壁承压型破坏。

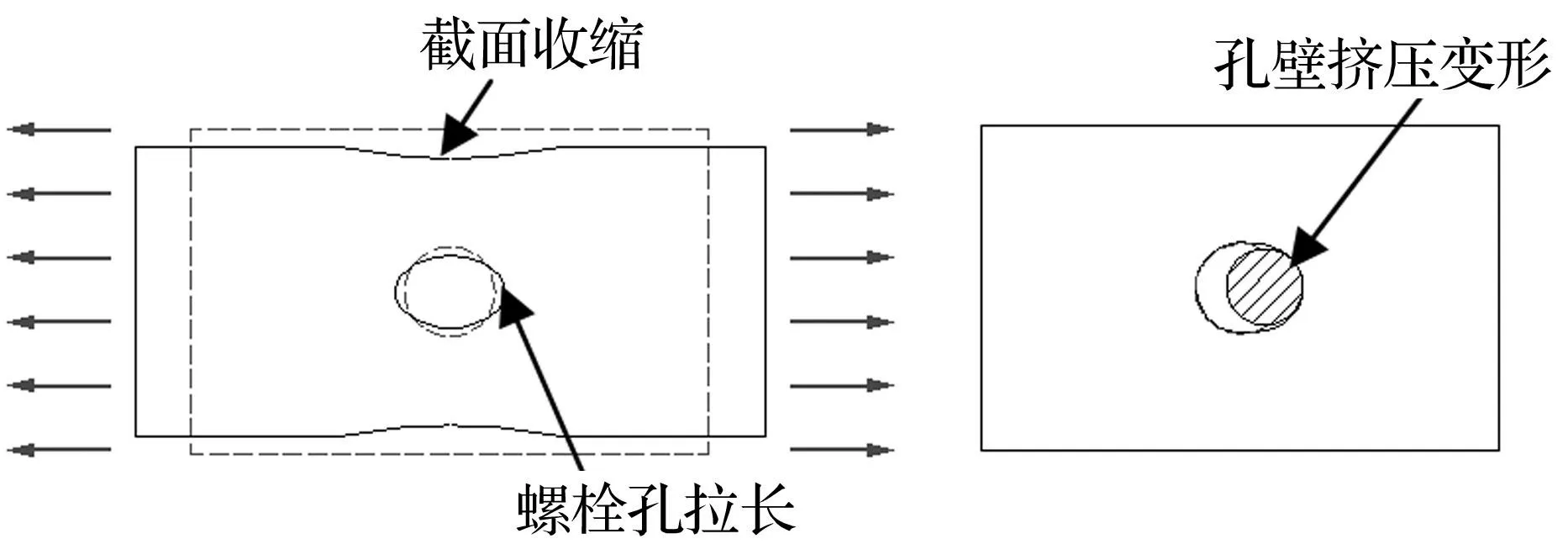
图14　螺栓孔变形示意图 Fig.14 Schematic view of bolt hole deformation

螺栓剪力(即螺栓孔承担的压力)随柱顶竖向位移发展曲线及盖板或梁下翼缘开裂前螺栓孔变形形状见图15，图中(d)为螺栓孔开始发展塑性至传力失效柱向下移动的距离。由图15看出，NC-NF及WC-NF模型螺栓孔处截面均出现收缩现象，表明螺栓孔断裂主

图15　螺栓剪力发展曲线 Fig.15 Shear force development in the bolts

要由板件受拉引起。WC-WF模型开裂前相应截面未发生明显收缩，表明净截面抗拉承载力大于螺栓孔抗压承载力，螺杆挤压为导致螺栓孔开裂的主要原因。因螺栓剪力与梁下翼缘(Ⅳ点)拉应力发展相符(图10)，均在开裂前保持稳定、开裂后迅速降低，稳定阶段即为塑性发展阶段。d值可反映螺栓孔的塑性变形能力，对比知，WC-WF模型d值远大于NC-NF及WC-NF。通过调整盖板尺寸、局部增大连接处梁下翼缘宽度，使螺栓孔发生孔壁承压型破坏，可提高螺栓孔的变形能力，进而大幅提高节点承载力。

4结论

通过数值模拟分析3个不同构造的矩形钢管柱-H形钢梁隔板贯通式全螺栓连接节点在连续性倒塌工况下性能，结论如下：

(1)节点子结构梁下翼缘与盖板在螺栓传力过程中，分别在内、外排螺栓处受力最大；增大盖板尺寸，使初始断裂破坏位置移至弯矩较小的外排螺栓处，可提高节点的承载力。

(2)同时增大连接区域梁下翼缘宽度及盖板宽度，使梁下翼缘连接处螺栓孔发生孔壁承压型破坏，可提高螺栓孔变形能力、延缓模型开裂，使截面受拉承载力充分发挥，利于悬链线作用发展，能大幅提高节点承载力。

(3)建议采用宽盖板、梁下翼缘局部增大的节点形式，以提高其抗连续性倒塌能力。

参考文献

[1]李玲,王伟,陈以一,等. 结构连续性倒塌工况下的梁柱节点研究现状[C].上海:第二届建筑结构抗倒塌学术交流会, 2012:155-161.

[2]Rölle L U K. Partial-strength and highly ductile steel and composite joints as robustness measure[C]. Proceeding of the Nordic Steel Conference,2009.

[3]Yang B, Tan K H. Different type of steel joint under catenary action part1: experimental test[C]. 6th Conference on Steel and Composite Structures, Budapest, Hungary, European Convention for Constructional Steelwork, 2011.

[4]Yang B, Tan K H. Different types of steel joints under catenary action part 2: numerical simulations[C]. 6th Conference on Steel and Composite Structures, Budapest, Hungary, European Convention for Constructional Steelwork, 2011.

[5]Yang B, Tan K H. Experimental tests of different types of bolted steel beam-column joints under a central-column-removal scenario[J].Engineering Structures,2013,54:112-130.

[6]Yang B, Tan K H. Robustness ofbolted-angle connections against progressive collapse: experimental tests of beam-column joints and development of component-based models [J]. Journal of Structural Engineering, 2013,139(9): 1498-1514.

[7]Lee C H, Kim S, Lee K. Parallel axial-flexural hinge model for nonlinear dynamic progressive collapse analysis of welded steel momentframes[J]. Journal of Structural Engineering, 2009, 136(2): 165-173.

[8]Main J A, Lew H S, Robert S D, et al. An experimental and computational study of steel moment connections under a column removalscenario [M]. US Department of Commerce, National Institute of Standards and Technology, 2010.

[9]Sadek F, Main J A, Lew H S, et al. Testing and analysis of steel and concrete beam-column assemblies under a column removal scenario[J]. Journal of Structural Engineering, 2011, 137(9): 881-892.

[10]Lew H S, Main J A, Robert S D, et al. Performance of steel moment connections under a column removal scenario. I:experiments[J]. Journal of Structural Engineering,2012, 139(1): 98-107.

[11]Sadek F, El-Tawil S, Lew H S. Robustness of composite floor systems with shear connections: modeling, simulation, andevaluation [J]. Journal of Structural Engineering, 2008, 134(11): 1717-1725.

[12]Li L, Wang W, Chen Y, et al. Experimental investigation of beam-to-tubular column moment connections under column removal scenario[J]. Journal of Constructional Steel Research, 2013, 88: 244-255.

[13]王伟,李玲,陈以一. 方钢管柱-H形梁栓焊混合连接节点抗连续性倒塌性能试验研究[J].建筑结构学报,2014, 35(4): 57-64.

WANG Wei, LI Ling, CHEN Yi-yi. Experimental investigation on progressive collapse behavior of WUF-B connections between SHS column and H beam [J].Journal of Building Structures, 2014, 35(4):57-64.

[14]王伟,李玲,陈以一,等. 圆钢管柱-H形梁外环板式节点抗连续性倒塌性能试验研究[J].建筑结构学报,2014,35(7):26-33.

WANG Wei, LI Ling, CHEN Yi-yi,et al. Experimental study on progressive collapse behavior of CHS column-to-H beam connections with outer-diaphragm[J]. Journal of Building Structures, 2014, 35,35(7):26-33.

[15]General services administration (GSA). Progressive collapse analysis and design guidelines for new federal office buildings and major modernization projects[S]. 2003.

[16]Department ofdefense (DoD). Design of buildings to resist progressive collapse, unified facilities criteria (UFC) 4-02303 [S]. 2009.