基于多重调谐质量阻尼器的滚珠丝杠副横向振动控制

2015-12-30王民,李凤蛟,昝涛等

振动与冲击 2015年10期

第一作者王民男，博士，教授，1972年生

王民，李凤蛟，昝涛，高相胜(北京工业大学机械工程与应用电子技术学院先进制造技术北京市重点实验室,北京100124)

摘要：为克服滚珠丝杠副动态特性随螺母沿丝杠运动不断变化，导致丝杠振动难以控制问题，提出采用多重调谐质量阻尼器对滚珠丝杠副横向振动进行控制。建立含多重调谐质量阻尼器的滚珠丝杠副在螺母及两端轴承处弹性支撑条件的动力学模型，获得不同螺母运动、受动态工作负载激励时丝杠横向振动频率响应函数。以不同螺母位置丝杠横向振动频率响应函数幅值最大值最小化为优化目标，获得多重调谐质量阻尼器最佳动力参数。仿真计算结果表明，采用多重调谐质量阻尼器进行丝杠横向振动控制，其效果及鲁棒性显著。

关键词：滚珠丝杠；振动控制；多重调谐质量阻尼器；参数优化

基金项目：国家重大科技专项(2012ZX04010-021-04)

收稿日期：2014-03-19修改稿收到日期：2014-04-24

中图分类号:TH113.1文献标志码：A

基金项目：国家自然科学

Bending vibration control of a ball screw via multi-tuned mass dampers

WANGMin,LIFeng-jiao,ZANTao,GAOXiang-sheng(Beijing Municipal Key Lab of Advanced Manufacturing Technology, College of Mechanical Engineering and Applied Electronic Technology, Beijing University of Technology, Beijing 100124, China)

Abstract:A ball screw system is widely used as a mechanical transmission unit. As the structure of the ball screw is long and narrow, the high speed performance of the screw is affected by its bending vibration. In addition, the resonance frequencies of the screw exist in a big range due to the movement of its nut. To overcome this problem, multi-tuned mass dampers were used to control the bending vibration of the ball screw here. After establishing the dynamic model of the screw with multi-tuned mass dampers, the frequency response function for the bending vibration of the screw was calculated. To control the bending vibration of the screw with the variation of its nut position, a numerical optimization algorithm was used to obtain the optimal design parameters of the multi-tuned dampers. The simulation results showed that the multi-tuned mass dampers have a good performance to control the bending vibration of the screw.

Key words:vibration control; ball screw; multi-tuned mass damper; parametric optimization

作为数控机床伺服进给系统中应用最广的机械传动部件—滚珠丝杠副由丝杠、螺母组成，可实现丝杠旋转运动到螺母直线运动转换。由于丝杠结构为细长轴，尤其在大型数控机床中，工作台行程较长，丝杠长径比很大，导致丝杠进给系统刚性及抗振性能下降，丝杠副临界速度受横向固有频率限制难以提高。随数控机床进给、切削速度不断提高，对滚珠丝杠副的临界转速及抗振特性提出更高要求。为此，本文提出采用多重调谐质量阻尼器(Multiple Tuned Mass Damper, MTMD)设计抗振滚珠丝杠，在空心丝杠中设置多重调谐质量阻尼器进行横向振动控制，以提高滚珠丝杠副的抗振性能及临界转速。

多重调谐质量阻尼器最早由Xu等[1]提出，与单个调谐质量阻尼器(TMD)相比，具有抗振频带宽、抑振效果及控制鲁棒性好等优点[2]，已成功用于桥梁等大型结构振动控制及机床切削颤振控制[3-4]。滚珠丝杠副因丝杠螺母随机床进给在整个行程上连续移动，导致丝杠固有频率、振型均有较大改变。较单阻尼器，多重调谐质量阻尼器因具有更好的控制频带宽、控制效果与鲁棒性，非常适合于滚珠丝杠副的横向振动控制。

多重调谐质量阻尼器动力学参数较多，得到最佳控制效果需进行多参数优化设计。已有研究对不同控制对象提出多重调谐质量阻尼器参数优化方法及优化目标函数[5-9]。本文为获得滚珠丝杠副横向振动最佳控制效果，建立符合实际工况的滚珠丝杠副在螺母及两端轴承处弹性支撑条件的动力学模型，获得螺母位置受动态工作负载激励时丝杠横向振动频率响应函数。并考虑螺母位置移动对丝杠横向振动影响，获得螺母位置沿丝杠轴向变动时的频率响应函数最大值。以该最大值的最小化为优化目标采用Minimax优化方法[10]进行优化，获取考虑螺母位置变动下丝杠横向振动频率响应幅值最小化的多重调谐质量阻尼器的最佳动力参数。

1丝杠横向振动振型函数

滚珠丝杠传动系统中，丝杠与螺母及两端轴承间均会产生接触变形。本文将丝杠等效成欧拉伯努利梁，丝杠两端轴承及螺母与丝杠间接触刚度均用径向支撑刚度表示，两端轴承支撑刚度分别用kv1、kv2表示，螺母与丝杠的径向支撑刚度用kv表示。以丝杠左端点为坐标原点，丝杠长度为L，螺母位置为L1,横截面积为A，则丝杠模型简化见图1。

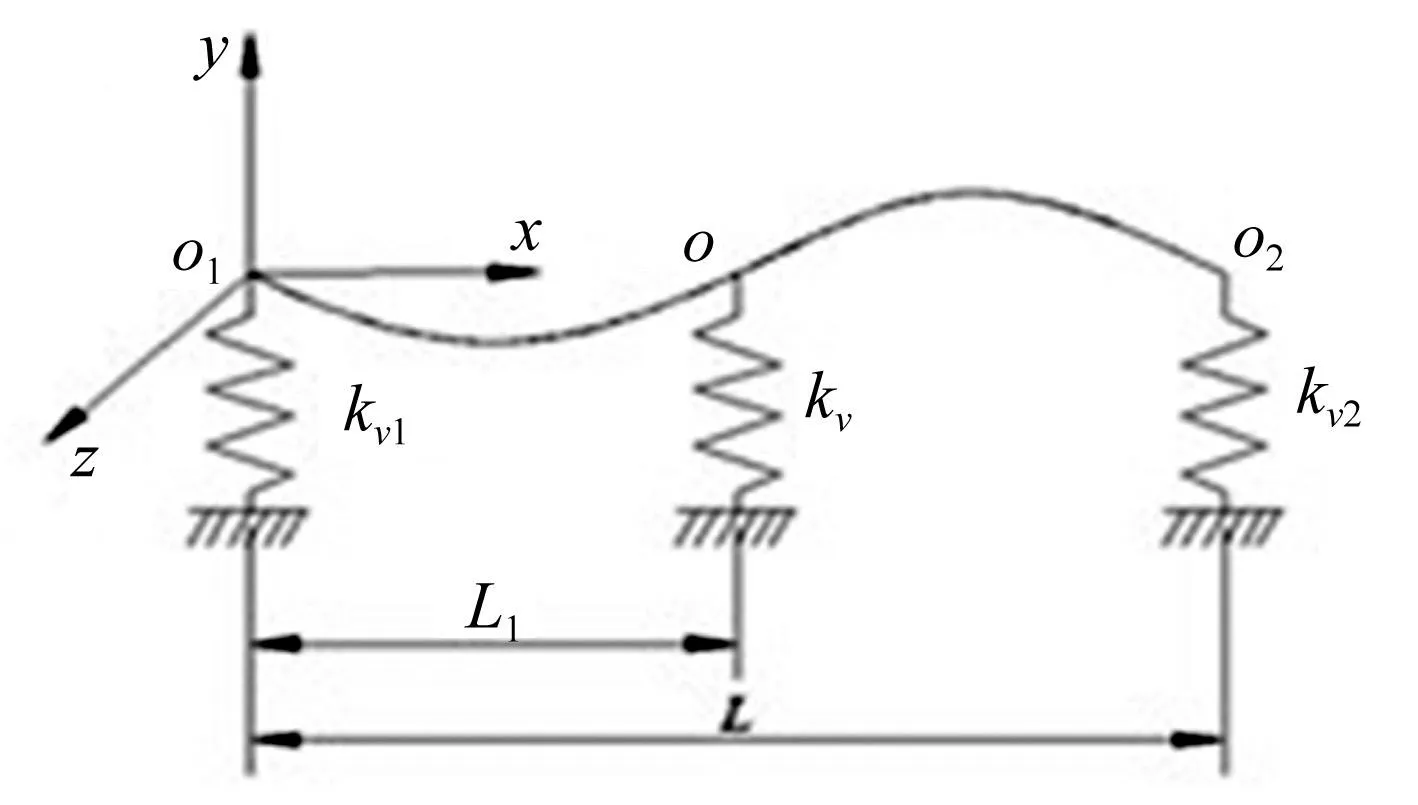
图1　丝杠横向振动支撑模型 Fig.1 Supporting model of transverse vibration of screw

梁横向弯曲振动振型函数为

Y(x)=D1ch(λx)+D2sh(λx)+

D3cos(λx)+D4sin(λx)

(1)

式中：λ4=Αω2ρ/(ΕΙ)，ω为丝杠横向振动固有频率，ρ为丝杠密度，EI为弯曲刚度；D1～D4为模态振型系数。

据式(1)，O1O段振型函数为

Y1(x)=C1ch(λx)+C2sh(λx)+

C3cos(λx)+C4sin(λx)

(2)

OO2段振型函数为

Y2(x)=C5ch(λx)+C6sh(λx)+

C7cos(λx)+C8sin(λx)

(3)

据O1，O2点的支撑条件有

(4)

(5)

(6)

(7)

丝杠左右两部分在O点连续，位移、弯矩、转角相等，有

Y1(L1)=Y2(L1)

(8)

(9)

(10)

据O点剪力关系有

(11)

由式(1)～式(8)可推导出振型系数C1～C8，从而求出丝杠横向振动振型函数。为便于分析计算，对丝杠振型函数进行质量归一化，丝杠k阶模态质量为

(12)

丝杠各阶归一化振型函数为

(13)

式中：φk,1，φk,2为丝杠O1O，OO2段k阶振型函数；Ck,n(n=1,2…,8)为丝杠k阶振型函数系数。

为表达简单，用φk代替φk,1，φk,2。实际计算中通过判断丝杠某点位置x与螺母位置L1的关系决定φk代表哪段的振型函数。

2丝杠横向振动幅频响应函数

含MTMD的滚珠丝杠副系统简化模型见图2。考虑实际中滚珠丝杠副外力为螺母处所受负载，设工作台施加给螺母的横向负载为简谐力F(t)=F0eiωt，F0为幅值，ω为频率。

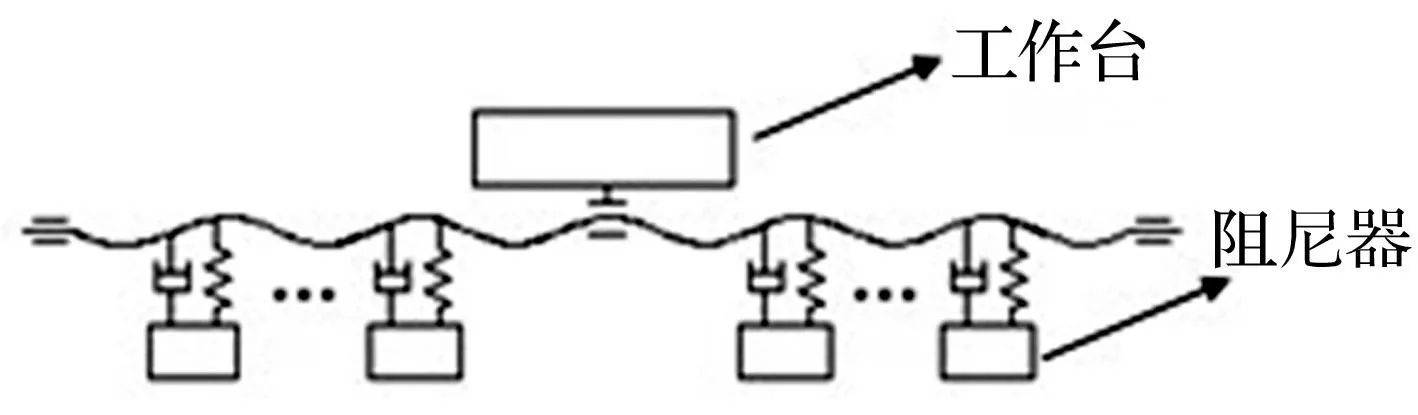
图2　含MTMD滚珠丝杠示意图 Fig.2 Diagram of ball screw with MTMD

工作台及螺母位置的移动会导致丝杠各阶固有频率、模态振型不断变化。某螺母位置L1处、丝杠第k阶模态动力学模型见图3。

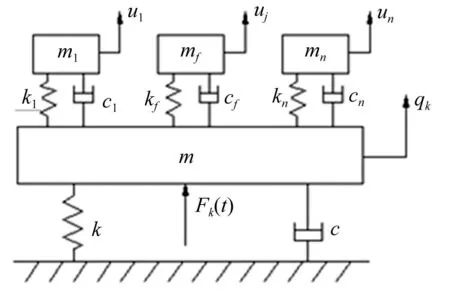
图3　含MTMD滚珠丝杠系统第k阶模态动力学模型 Fig.3 The dynamic model ofthe k th mode of the ball screw system with MTMD

则丝杠k阶模态外力为

Fk(t)=F(t)φk(L1)

(14)

式中：φk(L1)为k阶模态螺母处振型值。

含MTMD滚珠丝杠系统动力学方程为

F0φk(L1)eiωt

(15)

(16)

uj=yk,j+qkφ(aj)

(17)

式中：qk，uj，yk,j分别为丝杠k阶模态位移、第j个阻尼器自身位移及与丝杠k阶模态相对位移，j=1,…,n，n为阻尼器个数；ωk，ξk分别为丝杠k阶模态固有频率、阻尼比；mj，kj，cj分别为第j个阻尼器质量、刚度及阻尼；φk(aj)为k阶模态第j个阻尼器安装处振型值。

(18)

(19)

考虑简谐模态力Fk(t)=Fφk(L1)eiωt，k阶模态响应位移及阻尼器与k阶模态间相对位移表示为

qk(t)=Hqk(ω)eiωt

(20)

(21)

将式(20)、(21)代入式(18)、(19)，整理得滚珠丝杠第k阶模态频响函数为

(22)

螺母在L1处、丝杠轴向x处，含各阶模态的横向振动频率响应函数为

H(ω,L1,x,mj,ωj,ξj)=

(23)

式中：mn为模态数量。

为分析方便，引入无量纲变量及频响函数

vk=ω/ωk

(24)

γk,j=ωj/ωk

(25)

(26)

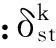
(27)

将无量纲变量代入式(22)得k阶模态无量纲频响函数为

(28)

为求出丝杠轴向不同处考虑前mn阶模态的横向振动频响函数，引入无量纲变量为

v=ω/ω1

(29)

γj=ωj/ω1

(30)

βk=ωk/ω1

(31)

(32)

Hg=H/δst

(33)

为分析方便，与频率相关的两无量纲优化参数ν，γj分别为频率变量及各TMD固有频率与所有L1取值时丝杠各阶模态固有频率中最低值之比。将无量纲变量代入式(23)，可得螺母在L1出、丝杠轴向x处横向振动无量纲频率响应函数为

Hg(v,L1,x,mj,γj,ξj)=

(34)

3MTMD优化方法

丝杠副传动时丝杠做旋转运动，螺母带动工作台做直线运动。为保证机床加工过程的平稳性，抑制工作台振动，以螺母处丝杠横向振动频响函数最大幅值最小化为优化目标。为尽量保证在工作台整个行程中振动始终得到有效控制，需对螺母运动不同位置的频响函数进行优化。优化目标为丝杠各阶模态引起的螺母位置丝杠频响函数最大幅值最小。

设计MTMD减振丝杠时，每个TMD沿轴向均布在中空丝杠内，在MTMD总质量一定前提下，调整各TMD参数，即mj，γj，ξj，使其在前两阶丝杠模态频率范围内，螺母在不同位置时丝杠无量纲频响函数最大幅值尽量最小。因此优化目标函数可定义为

(35)

MTMD参数优化算法为

(36)

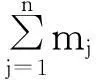
(37)

据式(36)、(37)，用MATLAB软件的Minimax算法进行优化，以获取MTMD最优化参数。

4仿真分析及结果

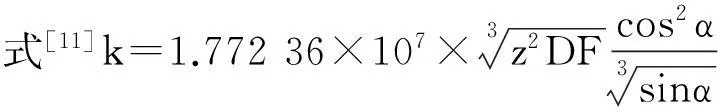
本文采用MTMD各阻尼器等质量等间隔分布，以各TMD频率比、阻尼比为优化参数。为考察TMD个数对优化效果影响，采用两种MTMD阻尼器布置方案，两种方案阻尼器总质量相等。方案一为5个TMD均布于空心丝杠中，每个TMD质量0.09 kg。方案二为9个TMD均布于空心丝杠中，各TMD质量为0.05 kg。考虑螺母位置相对于丝杠中心点对称时其频率响应幅频特性相同，因此阻尼器对称等间隔分布。为提高优化计算效率，令阻尼器优化参数、阻尼比相等。

无阻尼器、方案一、二优化后所得螺母位置丝杠横向振动幅频特性见图4～图6。方案一优化后各TMD频率比分别为3.10，0.82，1.09，0.82及3.10，各阻尼器位置分别为1L/6，2L/6，3L/6，4L/6及5L/6，各阻尼器阻尼比均0.155。方案二优化后各TMD频率比分别为2.91，3.34，0.98，0.83，1.44，0.83，0.98，3.34及2.91，各阻尼器位置为1L/10，2L/10，3L/10，4L/10，5L/10，6L/10，7L/10，8L/10及9L/10，各阻尼器阻尼比均为0.098。

对比两种优化结果与不加阻尼器看出，用MTMD控制丝杠螺母处横向振动效果显著。方案一与无阻尼器时相比，所有螺母处频响函数最大振幅减小89.8%，方案二与无阻尼器时相比，所有螺母处频响函数最大振幅减小90.3%。因此在MTMD总质量相同情况下，阻尼器个数越多抑制振动效果越明显。在空心丝杠中加入阻尼器且在结构尺寸允许条件下，阻尼器个数尽量多些，以达到更好的抑振效果。

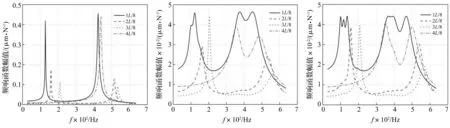
图4 无阻尼器时螺母位置丝杠频响函数Fig.4Frequencyresponseofthescrewwithoutdampers图5 方案一螺母位置处丝杠频响函数Fig.5Optimalresultsforcase1图6 方案二螺母位置处丝杠频响函数Fig.6Optimalresultsforcase2

图7　方案二非优化用螺母位置丝杠频响函数 Fig.7 Frequency response prediction for case 2

为考察MTMD抑制丝杠横向振动的鲁棒性，选2L/10、3L/10及4L/10三个非优化用螺母位置，采用方案二优化所得的MTMD参数进行频响函数仿真计算，结果见图7。

由图7看出，三个非优化用螺母位置，丝杠横向振动频响函数最大幅值得到有效控制，表明本文所用MTMD优化算法可保证丝杠整个行程上螺母处横向振动能有效控制。

5结论

本文针对丝杠副横向振动控制问题，采用MTMD方法实现全行程螺母位置丝杠横向振动的有效控制。通过仿真实验结论如下：

(1)MTMD方法控制丝杠横向振动效果显著。通过优化设计MTMD参数，螺母处横向振动幅值可减少约90%。

(2)所用MTMD优化方法能保证全行程螺母在不同位置，丝杠横向振动均能得到有效控制。

(3)MTMD阻尼器总质量一定时，丝杠中加入的阻尼器个数越多，抑振效果越好。

参考文献

[1]Xu K，Igusa T．Dynamic characteristics of multiple substructures with closely spaced frequencies[J]. Earthquake Engineering and Structural Dynamics,1992，21:1059-1070．

[2]李春祥,熊学玉,王肇民．结构-MTMD系统的动力特性研究[J]．振动与冲击,1999,18(4)：52-54．

LI Chun-xiang,XIONG Xue-yu,WANG Zhao-min．Research on dynamic characteristics of structure MTMD system[J]．Journal Vibration and Shock，1999，18(4)：52-54．春祥,熊学玉,王肇民．结构-MTMD系统的动力特性研究[J]．振动与冲击,1999,18(4)：52-54．

LI Chun-xiang,XIONG Xue-yu,WANG Zhao-min．Research on dynamic characteristics of structure MTMD system[J]．Journal Vibration and Shock，1999，18(4)：52-54．

[3]汪正兴,任文敏,苏继宏,等．多重调谐质量阻尼器参数优化的一种改进算法及其应用[J]．工程学力,2005, 22(5)：26-30．

WANG Zheng-xing,REN Wen-min,SU Ji-hong,et al. An improved optimization algorithm for MTMD system and its application[J]，Engineering Mechanics，2005,22(5):26-30．

[4]杨毅青,刘强,王民．面向车削颤振抑制的多重阻尼器优化设计[J].振动工程学报,2010,23(4):468-474．

YANG Yi-qing，LIU Qiang，WANG Min．Optimization of multiple tuned mass dampers for chatter suppression in turing[J]，Journal of Vibration Engineering，2010，23(4):468-474．

[5]李春祥,熊学玉．结构被动和主动多重调谐质量阻尼器控制策略的发展[J].四川建筑科学研究,2003， 29(2): 88-91．

LI Chun-xiang,XIONG Xue-yu．Development of control strategies of passive and active multiple tuned mass dampers for structures[J].Sichuan Building Science,2003,29(2):88-91．

[6]刘耀宗,郁殿龙,赵宏刚,等．被动式动力吸振技术研究进展[J].机械工程学报,2007,43(3):14-21．

LIU Yao-zong,YU Dian-long,ZHAO Hong-gang,et al. Review of passive dynamic vibration absorbers[J]. Journal of Mechanical Engineering,2007,43(3):14-21.

[7]Hoang N， Warnitchai P．Design of multiple tuned mass dampers by using a numerical optimizer[J]. Earthquake Engineering and Structural Dynamics，2005 (34):125-144．

[8]LI Hong-nan，NI Xiang-lei．Optimization of nonuni-formly distributed multiple tuned mass damper[J]. Journal of Sound and Vibration,2007 (308):80-97．

[9]Zuo L,Nayfeh S A．The multi-degree-of-freedom tuned-mass damper for suppression of single-mode vibration under random and harmonic excitation [J]. ASME Conference Proccdings,2003,37(33):2051-2061．

[10]Dem’yanov V F.Introduction to minimax[M]. New York:Wiley,1974．

[11]戴曙．机床滚动轴承应用手册[M] ．北京：机械工业出版社,1993:163-166． K，Igusa T．Dynamic characteristics of multiple substructures with closely spaced frequencies[J]. Earthquake Engineering and Structural Dynamics,1992，21:1059-1070．