含区间参数的齿轮系统扭振固有特性研究

第一作者魏莎女，博士生，1988年2月生

通信作者褚福磊男，博士，教授，博士生导师，1959年9月生

邮箱：chufl@mail.dtinghua.edu.cn

含区间参数的齿轮系统扭振固有特性研究

魏莎，韩勤锴，褚福磊(清华大学摩擦学国家重点实验室，北京100084)

摘要：为研究啮合刚度等动力学参数的波动性对齿轮传动系统固有特性影响，以四自由度扭转振动齿轮传动系统模型为例，利用区间模态分析方法对含区间动力学参数齿轮系统模态特性进行分析。通过算例给出齿轮系统固有频率波动区间，并通过上下边界相对不确定量与曲线凹凸性分析区间参数对系统固有频率影响。结果表明，参数波动导致的区间固有频率并非关于确定性模型下固有频率中心对称，而存在上下偏差，导致该偏差的主要原因为曲线凹凸性；通过上下边界相对不确定量及凹凸性可判断固有频率随系统参数的波动规律，上下边界相对不确定量间差异越大曲线凹凸性越明显。在单区间参数分析中，不同区间动力学参数对系统固有频率影响不同。当所有参数区间波动均考虑时系统区间固有频率范围最大，超过工程能接受结果，因此设计分析时参数的区间波动性不可忽略。

关键词：齿轮；固有频率；模态；区间分析

收稿日期：2014-03-10修改稿收到日期：2014-04-30

中图分类号:TH132.41；TH113.1文献标志码：A

Natural characteristics analysis for torsional vibration of a geared transmission system with uncertainties

WEISha,HANQin-kai,CHUFu-lei(State Key Laboratory of Tribology, Tsinghua University, Beijing 100084, China)

Abstract:The torsional vibration model of a geared transmission system with 4-DOF was developed to study the natural characteristics of a gear system considering fluctuations of tooth mesh stiffness and other dynamic parameters. The interval modal analysis method, relative uncertainties and the curve concavity and convexity analysis were used to investigate the modal characteristics of the gear system with interval varying dynamic parameters. The fluctuation intervals of its natural frequencies were obtained with a numerical example. The results showed that the natural frequencies of the deterministic model are not the central values of the interval varying natural frequencies caused by parameter fluctuations, there are upper and lower deviations caused by the curve concavity and convexity; the fluctuating laws of the natural frequencies with fluctuating parameters can be determined with the relative uncertainties of the upper and lower bounds and the curve concavity and convexity; the greater the differences between the relative uncertainties of the upper and lower bounds, the more obvious the corresponding curve concavity and convexity; the effects of different interval dynamic parameters on the natural frequencies are different in a single interval parametric analysis; the interval natural frequencies are largest and exceed the acceptable results of engineering when the fluctuations of all the corresponding parameters are taken into account; therefore, the effects of the interval fluctuations of system parameters on the natural frequencies of the gear system can not be ignored.

Key words:gear; natural frequencies; modal; interval analysis

齿轮传动系统广泛用于风力发电机组、直升机、汽车等机械设备。对其进行深入的动力学研究可为设备的安全、优化设计及可靠性评估奠定基础。目前齿轮系统动力学研究大多处理为确定性问题[1-3]，但制造、装配、润滑、冲击及温度等因素会导致齿轮系统参数具有不确定性，且理论分析的动力学模型往往进行一定简化，与实际模型存在误差，因此须进行不确定参数下的特性分析。齿轮系统动态特性不确定分析主要采用基于统计模型的分析方法[4-6]，而不确定性不等同于随机性，统计分析方法并非研究齿轮不确定问题的唯一方法。实际上，不确定分析的相关数学模型有统计模型、区间模型及模糊模型等，需针对具体问题据已知相关信息程度选择相应数学模型进行不确定性分析。其中区间模型无需大量样本实验或参数分布假设，在已知参数边界信息情况下，用相关区间算法给出结果所在区间及结果误差估计。区间分析方法在土木结构的模态特性分析中已有研究成果，如陈塑寰[7]提出的矩阵摄动法给出在小扰动下区间特征值的近似计算方法。Sim等[8]给出的计算结构系统模态区间分析方法，将n个区间特征值问题转化为2n个确定性特征值求解。而区间分析方法用于齿轮传动系统固有特性分析的相关研究较少。本文针对贫信息、小样本下已知参数信息，利用区间分析方法对具有区间参数的齿轮系统固有特性进行研究，并给出固有频率所在区间，分析区间参数对系统固有频率影响。

1系统模型及固有特性分析

图1为单对齿轮传动系统示意图，输入原动机、主被动齿轮及输出负载均等效为圆柱体，其中主被动齿轮等效圆柱厚度相同。图中Im、I1、I2、IL分别表示输入原动机、主动齿轮、从动齿轮、负载的转动惯量，km为齿轮副啮合刚度，ks1、ks2分别为主、被动连接轴扭转刚度，θm、θ1、θ2、θL为输入原动机、主动齿轮、从动齿轮、负载的扭转角位移，Tm、TL分别为作用于原动机、负载的外力矩。

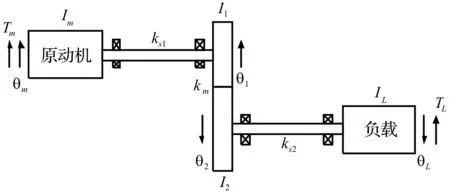
图1　齿轮传动系统纯扭转振动模型 Fig.1 Schematic diagram of torsional vibration model

本文仅研究齿轮传动系统的固有特性，其自由振动方程[9]为

(1)

式中：θ为振动位移向量；m，k分别为质量、刚度矩阵。具体表达式为

θ=[θmθ1θ2θL]T

(2)

(3)

(4)

主被动齿轮基圆半径R1、R2及转动惯量I1、I2以及主被动连接轴扭转刚度ks1、ks2计算式为

R1=mz1cos(α0/2),R2=mz2cos(α0/2)

(5)

(6)

(7)

式中：ρ为质量密度；b为有效齿宽；G为剪切模量，可由式(8)求得；m为齿轮模数；α0为压力角；z1，z2为主、被动轮齿数；Ra1，Ra2为主、被动连接轴半径；la1，la2为主、被动连接轴长。

G=E/(2(1+υ))

(8)

式中：E为弹性模量；υ为泊松比。

确定性参数下的第i阶特征值λi满足

kΦi=λimΦi

(9)

式中：Φi为λi对应的主振型(质量正则化)。

取齿轮传动系统基本参数[10]见表1，计算得确定参数下固有频率为0 Hz、266 Hz、524 Hz、3362 Hz，振型见图2。图2中点划线表示模态参考位置，实线表示由确定性参数计算所得模态阵型。由图2看出，二阶模态在负载处振动最大，其次为原动机，而主被动齿轮处振动不明显。

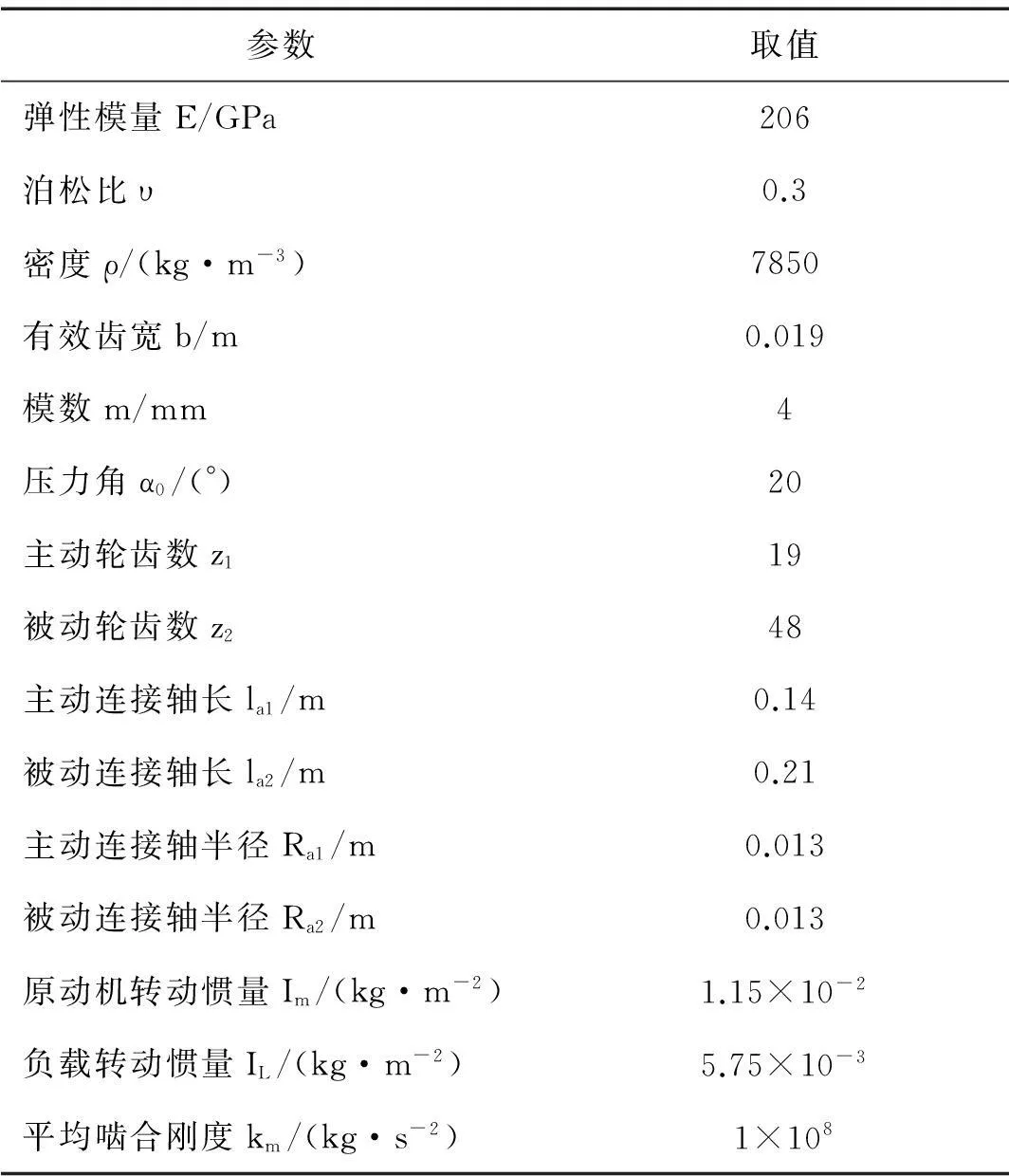
表1　基本计算参数

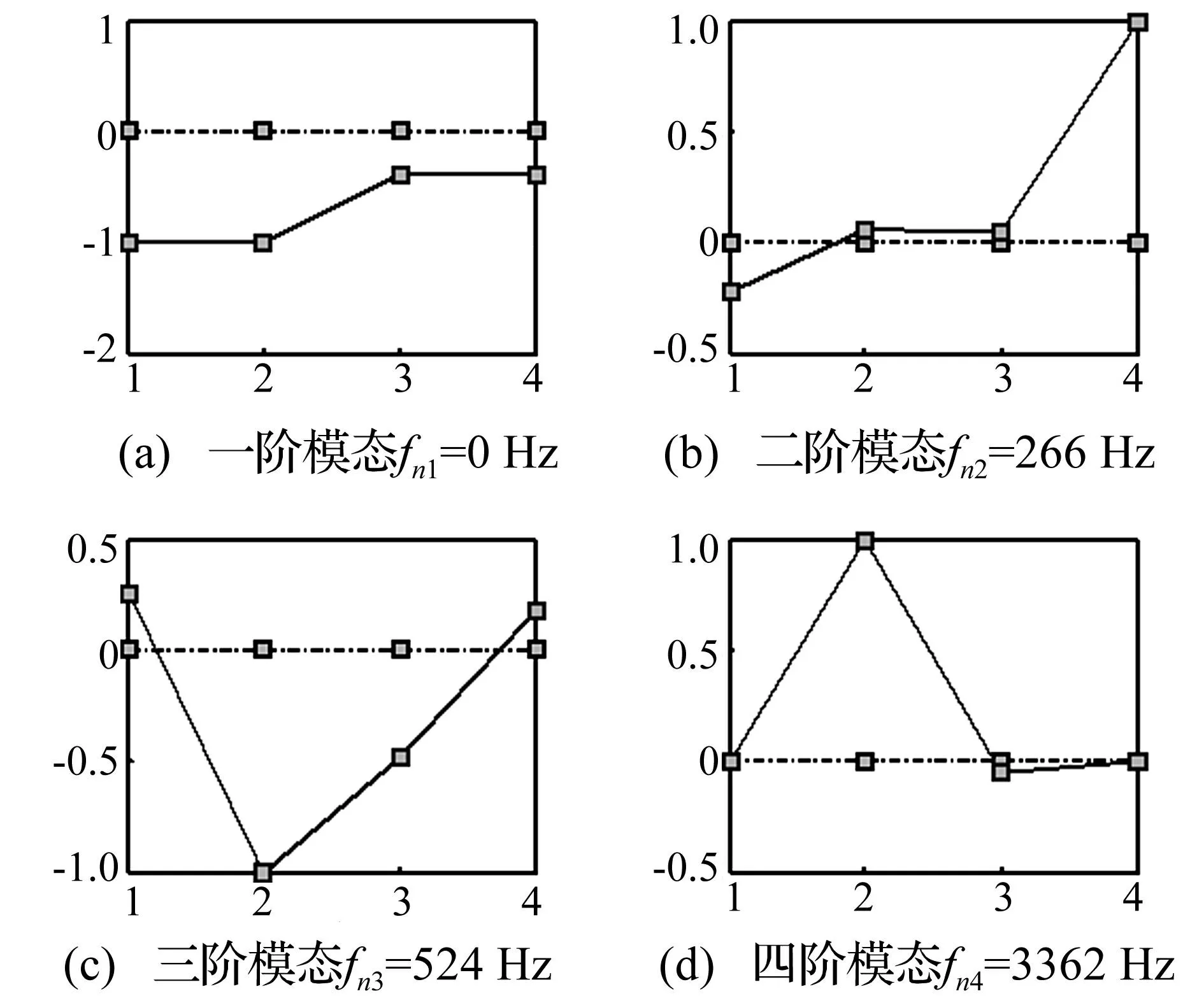
图2　齿轮系统振型图 Fig.2 Mode shapes of the gear system

2区间模态分析

以上为齿轮传动系统扭转振动的确定性模态分析。而材料不均匀性、制造误差、测量误差及润滑等因素会导致系统的刚度、质量参数只能给出其近似值及绝对误差界限。本文中用区间参数表示为

aI=[ac-βac,ac+βac]

(10)

式中：aI为区间参数；ac为区间参数近似值；β为区间参数波动误差。

考虑参数的区间波动，原自由振动方程(1)转化为区间约束下振动方程为

(11)

式中：m，k为质量、刚度矩阵，满足

(12)

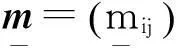
(13)

Chen等[11]基于Rayleigh商给出用于计算区间特征值问题的非迭代方法，其中第i阶特征值上下边界值可直接由计算式获得，即

(14)

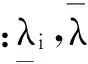
为考察各系统参数存在区间波动时系统固有频率变化，取相应参数为区间参数。区间原动机转动惯量可表示为

(15)

为分析方便，定义上、下边界相对不确定量μupper，μlower分别为

(16)

式中：

(17)

(18)

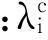
为验证本文齿轮系统动力学模型的正确性及区间分析方法精度及效率，考虑Im、I1、I2、IL均为区间参数，采用Monte Carlo分析方法对该算例固有频率模拟计算。其中区间参数近似值由表1取得。波动误差均为5%，统计分析样本数分别取1000、10000、100000，计算效率比较结果见表 2。由表2看出，区间分析方法耗时最短，而Monte Carlo分析方法计算时间随样本数增加而增加。较Monte Carlo分析方法，区间分析方法大大节省计算时间。Monte Carlo仿真取样100000次与区间分析方法对比结果见图3。由图3看出，区间分析方法结果较好包络Monte Carlo仿真分析结果。

表2　两种不确定分析方法计算效率比较

考虑Im、I1、I2、IL、km、ks1、ks2均为区间参数时，波动误差均取5%，利用各矩阵对区间参数的单调性可得对应区间质量、刚度矩阵分别为

图3 区间分析方法与蒙特卡洛仿真方法结果对比Fig.3ComparisonbetweentheintervalmethodandtheMonteCarlomethodwithfluctuationsofmomentsofinertia图4 齿轮系统区间固有频率及不确定量随β变化规律Fig.4Curvesofnaturalfrequenciesandrelativeuncertaintieswithfluctuationerrors

由式(14)所得第二阶固有频率见表 3。由表3看出，固有频率并非确定值，而是一个区间，且当相关动力学参数均考虑为区间参数，β取5%时，计算所得fn2的相对不确定量已达6%，超出工程能接受限值。图4为fn2随β及μlower、μupper随β的变化规律。由图4看出，随β增大齿轮系统固有频率区间宽度线性增大。当β达到15%时fn2的相对不确定量达18%，远超工程接受范围。因此在设计阶段，参数的区间波动性分析不可忽略。

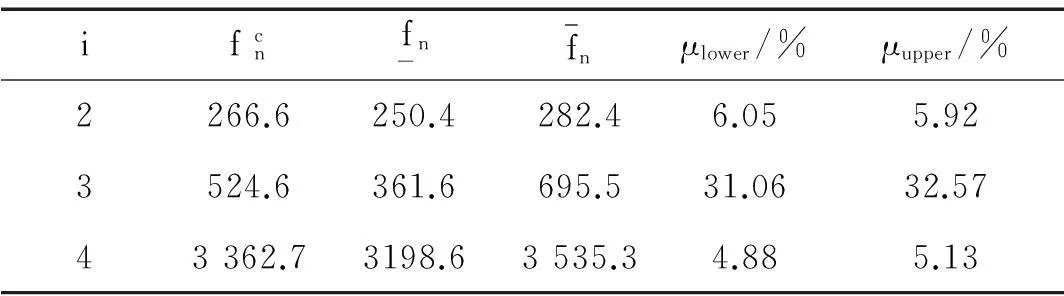
表3　齿轮系统区间固有频率

2.1区间质量参数对固有频率影响

Im、I1、I2、IL分别为区间参数时所得fn2及μlower、μupper随β变化规律见图 5～图8。由4图看出，不同区间动力学参数对系统固有频率影响亦不同。其中区间参数波动误差对齿轮系统区间固有频率影响明显，随β增大fn2线性增大；在Im、IL对fn2影响中，μlower、μupper不相等。该差异主要由参数的凹凸性所致，具体分析见图9。由图9看出，当函数曲线为凹弧时，对称参数区间对应的函数结果并非关于确定性模型下结果对称，而是上边界相对不确定量大于下边界；当函数曲线为凸弧时，对称参数区间对应的函数结果亦非关于确定性模型下结果对称，而是下边界相对不确定量大于上边界；且凹凸性越明显对应上下边界相对不确定量间差异越大。因此图5中μupper> μlower现象主要因Im与fn2间曲线关系为凹弧导致。由图5(c)看出，Im与fn2间曲线关系为凹弧，验证了通过上下边界相对不确定量得

图5　各种变化规律 Fig.5 Curves of natural frequencies

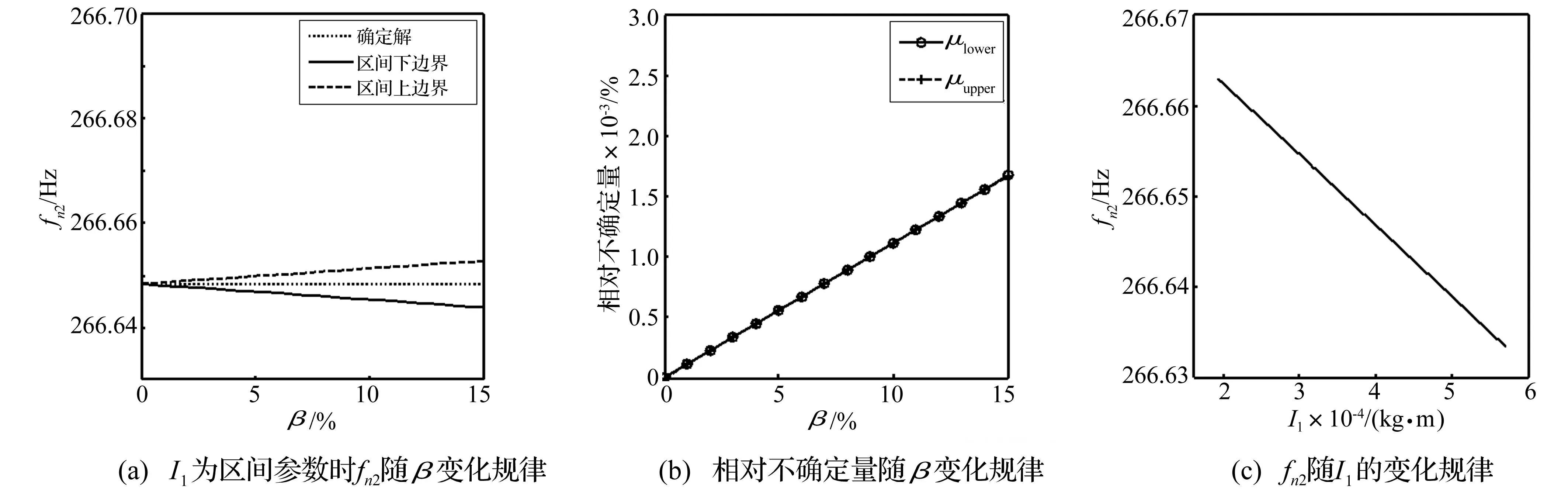
图6　各种变化规律 Fig.6 Curves of natural frequencies

图7　各种变化规律 Fig.7 Curves of natural frequencies

图8　各种变化规律 Fig.8 Curves of natural frequencies

到的推断。图8现象原因相同，不再赘述。图6(b)中当I1为区间参数时，fn2的相对不确定量随β线性增加；在相同波动误差下，上下边界相对不确定量相等。主要因I1与fn2间为线性关系，见图6(c)。图7(b)中，当I2为区间参数时fn2的相对不确定量随β线性增加；在相同波动误差下，上下边界相对不确定量近似相等，主要因I2与fn2间曲线关系近似线性，见图7(c)。

图9　曲线凹凸性分析 Fig.9 Concavity and convexity analysis

2.2区间刚度参数对固有频率影响

由于误差、碰撞及润滑等原因导致啮合刚度在齿轮啮合转动过程中存在不确定性波动，且在啮合刚度解析计算中所得结果与实测值误差一般在20%内[12]。考虑km、ks1、ks2为区间参数时，可得相应的fn2随β变化规律及μlower、μupper随β变化规律见图10～图12。由图10(a)、(b)看出，随β增大fn2非线性增大；在相同波动误差下μlower与μupper间差异较大，且μlower明显大于μupper，主要由啮合刚度与固有频率间曲线关系为凸弧引起，见图10(c)。由此表明齿轮啮合刚度对系统固有特性影响显著，应予以考虑。而ks2对fn2影响最明显，且为线性，见图12(c)。当β < 5%时km、ks1对fn2影响较小，而β继续增加时fn2的区间上下界差异明显。图11(b)中表现为μlower> μupper，主要因ks1与fn2的曲线关系为凸弧，见图11(c)。

图10　各种变化规律 Fig.10 Curves of natural frequencies

图11　各种变化规律 Fig.11 Curves of natural frequencies

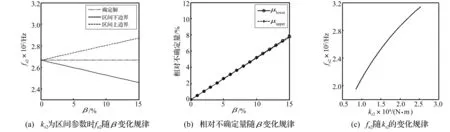
图12　各种变化规律 Fig.12 Curves of natural frequencies

3结论

(1)较Monte Carlo仿真等统计分析方法，区间模型无需大量样本实验及概率假设，结果可靠，节省计算成本。对具有不确定参数的动力学系统特性，据已知系统信息程度选择不同分析方法。系统参数信息无法获得或只能进行有限实验时，区间分析方法可直观给出计算结果的区间范围及相应误差估计。

(2)考虑系统动力学参数存在区间波动时所得固有频率也在一个区域内波动。且参数波动导致的区间固有频率并非关于确定性模型下固有频率中心对称，而存在上下偏差，主要原因为参数的凹凸性。通过凹凸性、上下边界相对不确定量可判断系统参数波动规律，进而推断区间固有频率受参数波动应注意的地方。

(3)当考虑所有参数区间波动时，系统区间固有频率范围最大。虽各动力学参数波动误差均较小，但累加后对固有频率影响较显著。设计时参数的区间波动性分析不可忽略。

(4)不同区间动力学参数对系统固有频率影响不同。区间参数的波动误差对齿轮系统区间固有频率影响明显。第二阶固有频率主要受负载转动惯量及被动连接轴扭转刚度影响。

(5)分别在原动机转动惯量、负载转动惯量、主动连接轴的扭转、啮合刚度对固有频率影响分析中，上下边界相对不确定量不相等，由凹凸性可判断其与固有频率间关系。主被动齿轮的转动惯量、被动连接轴扭转刚度与第二阶固有频率变化规律均为线性关系。

参考文献

[1]Han Q, Zhao J, Chu F. Dynamic analysis of a geared rotor system considering a slant crack on the shaft [J]. Journal of Sound and Vibration, 2012, 331(26): 5803-5823.

[2]Parker R G, Wu X. Vibration modes of planetary gears with unequally spaced planets and an elastic ring gear [J]. Journal of Sound and Vibration, 2010, 329(11): 2265-2275.

[3]杨通强，宋轶民，张策，等. 斜齿行星齿轮系统自由振动特性分析[J]. 机械工程学报, 2005, 41(7): 50-55.

YANG Tong-qiang, SONG Yi-min, ZHANG Ce,et.al. Property analysis of free vibration of helical planetary gear trains [J]. Chinese Journal of Mechanical Engineering, 2005, 41(7): 50-55.

[4]李润方，王建军. 国外齿轮系统动态特性的统计分析[J]. 机械传动, 1995, 19(4): 45-47.

LI Run-fang, WANG Jian-jun. Statistical analysis of characteristics for gear system at overseas[J]. Journal of Mechanical Transmission, 1995, 19(4): 45-47.

[5]Driot N, Perret-Liaudet J. Variability of modal behavior in terms of critical speeds of a gear pair due to manufacturing errors and shaft misalignments[J]. Journal ofSound and Vibration, 2006, 292(3): 824-843.

[6]魏永祥，陈建军，王敏娟. 随机参数齿轮-转子系统扭转振动固有频率分析[J]. 工程力学, 2011, 28(4): 172-177.

WEI Yong-xiang, CHEN Jian-jun, WANG Min-juan. Natural frequency analysis for torsional vibration of a gear-rotor system with random parameters [J]. Engineering Mechanics, 2011, 28(4): 172-177.

[7]陈塑寰. 结构动态设计的矩阵摄动理论[M]. 北京: 科学出版社, 1999.

[8]Sim J, Qiu Z, Wang X. Modal analysis of structures with uncertain-but-bounded parameters via interval analysis[J]. Journal of Sound and Vibration, 2007, 303(1/2): 29-45.

[9]李润方，王建军. 齿轮系统动力学-振动、冲击、噪声[M]. 北京: 科学出版社, 1997.

[10]Kahraman A, Ozguven H N, Houser D R, et al. Dynamic analysis of geared rotors by finite elements[R]. DTIC Document, 1990.

[11]Chen S, Qiu Z, Song D. A new method for computing the upper and lower bounds on frequencies of structures with interval parameters [J]. Mechanics Research Communications, 1994, 21(6): 583-592.

[12]李明，孙涛，胡海岩. 齿轮传动转子-轴承系统动力学的研究进展[J]. 振动工程学报, 2002, 15(3): 5-12.

LI Ming, SUN Tao, HU Hai-yan. Review on dynamics of geared rotor-bearing systems[J]. Journal of Vibration Engineering, 2002, 15(3): 5-12.