轮胎附着特性的胎面纵向振动建模与分析

第一作者左曙光男，博士，教授，博士生导师，1968年6月生

轮胎附着特性的胎面纵向振动建模与分析

左曙光，冯朝阳，吴旭东，段向雷(同济大学新能源汽车工程中心，上海201804)

摘要：通过对接地区域的胎面离散化处理，建立胎面纵向振动模型，引入动态摩擦模型-分布式LuGre模型，实现对滚动轮胎接地区域动态附着特性描述。针对某轮胎滚动工况，在Matlab/Simulink中进行数值模拟，通过调整模型参数，获得车速、胎压等对轮胎附着影响，验证模型的正确性、合理性；分析胎面接地区域摩擦力及位移的分布规律，为滚动轮胎纵向振动研究提供理论依据。

关键词：附着特性；胎面；动态摩擦模型；LuGre摩擦模型

基金项目：国家自然

收稿日期：2014-09-02修改稿收到日期：2014-11-11

中图分类号:U463.341文献标志码：A

基金项目：国家自然科学基金重点项目(51335006)，北京市自然科学基金重点项目(3131002)，清华大学摩擦学国家重点实验室自主研究课题(SKLT11A02)

Tread’s longitudinal vibration modeling and analysis for attachment characteristics of tire

ZUOShu-guang,FENGZhao-yang,WUXu-dong,DUANXiang-lei(Clean Energy Automotive Engineering Center, Tongji University, Shanghai 201804, China)

Abstract:In order to model the dynamic attachment characteristics of a rolling tire’s tread, a dynamic model of tread in its longitudinal direction was proposed. Considering the dynamic characteristics of friction on the tread’s contract area, LuGre dynamic friction distribution model was employed to describe the attachment features of the tread in the proposed model. Then a series of numerical simulations under various conditions were implemented using Matlab/Simulink. The model was verified and the influences of factors including vehicle speed and tire pressure on the tire’s attachment characteristics were obtained through adjusting the model’s parameters. Furthermore, the distribution laws of friction and displacement on the tread’s contract area were analyzed. The results provided a theoretical basis for studying rolling tire’s longitudinal vibration.

Key words:attachment characteristic; tread; dynamic friction model; LuGre friction model

轮胎通过与路面接触作用为汽车在水平方向提供制动、驱动及侧向稳定所需的力。轮胎作为弹性体，受到载荷与路面接触时会形成接触面，即胎面接地区域。由于轮胎的弹性迟滞及大变形等特性使接地区域的附着特性非常复杂。因此该特性的描述成为汽车轮胎学的重点、难点。对胎面橡胶摩擦已有不少研究，如Savkoor[1]通过试验得出橡胶的摩擦系数受滑移速度及温度影响较大，研究轮胎力学特性时应考虑路面附着系数变化；李勇等[2-3]考虑轮胎-路面摩擦的非线性，利用集中式LuGre模型分析轮胎胎面的自激振动，获得多边形磨损规律。刘昭度[4]提出轮胎-路面侧向动力学数学模型，描述侧向附着系数与车轮滑动率关系，建立纵向附着的动力学数学模型，考虑路况、车速、法向载荷影响，完善了Pacejka模型，使该模型适用于轿车的各种制动工况；庄晔[5]利用半经验模型分析动摩擦对轮胎侧偏特性影响；吴广政[6]通过一系列轮胎试验数据，用数学拟合方法获得轮胎纵向附着特性的数学模型。然而诸多研究一部分为由试验数据出发用数学拟合方法获得纵向模型，但模型参数并无具体物理意义；另一部分利用有限元建模方法获得仿真模型，可获得较直观结果，但在仿真过程中的参数多采用半经验方法，较多参数并不能与实际物理意义进行对应。

本文针对轮胎胎面纵向受力进行分析，建立轮胎胎面在纵向离散化动力学模型；再据实际行驶工况及所研究对象，对模型中所需重要参数进行识别与等效；利用Matlab/Simulink对理论模型进行数值仿真，对比分析车速、胎压等因素对轮胎附着影响，证明模型的正确性及合理性。

1胎面-路面附着特性分析

1.1胎面橡胶摩擦特性分析

轮胎胎面部分由分割成块的橡胶构成，且紧靠带束，带束层刚度较橡胶刚度大，因此可用橡胶块模型[7]，见图1。汽车轮胎与路面属典型的干摩擦系统，其摩擦力大小与摩擦副的相对滑动速度有复杂的非线性关系[8]，见图2。

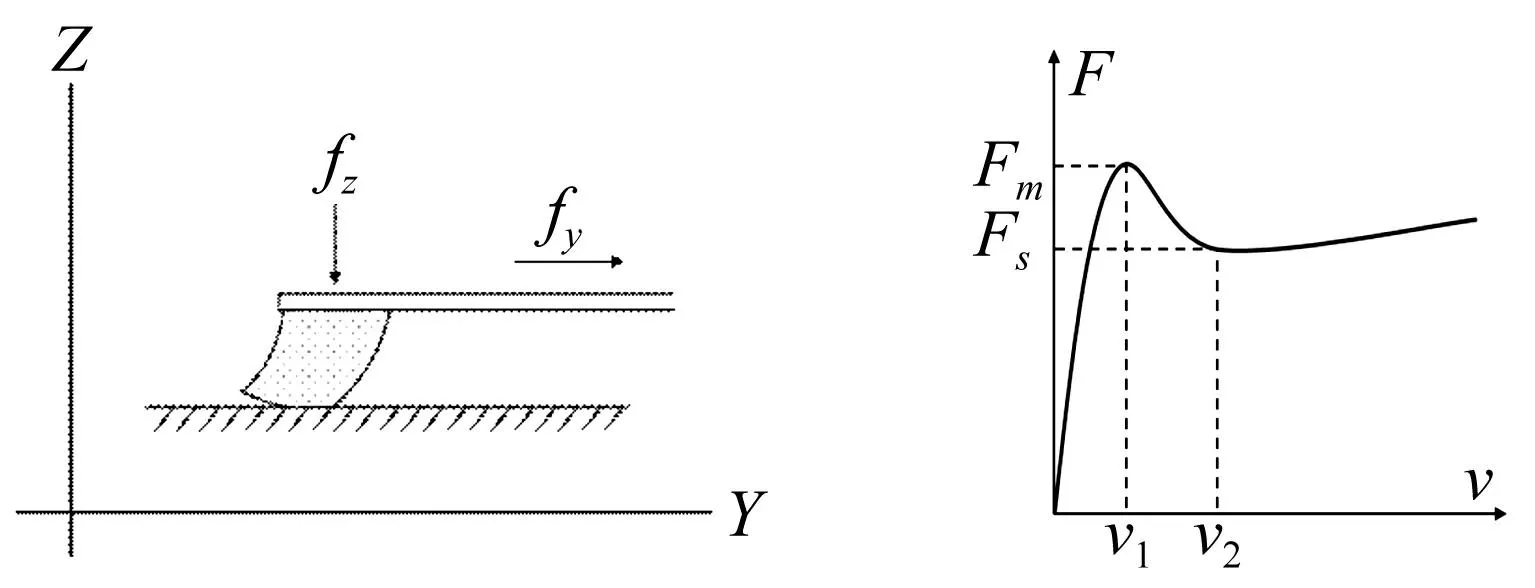
图1 胎面橡胶变形Fig.1Deformationoftreadrubber图2 胎面橡胶摩擦力与相对滑动速度关系Fig.2Relationshipbetweentreadrubberfrictionandslidingvelocity

当v∈[0,v1]时，胎面与路面处于粘滞状态，摩擦力属于静摩擦，摩擦力大小与滑动速度基本呈线性关系且斜率较大。在v=v1处F达到最大值Fm，即为最大静摩擦力。当v∈[v1,v2]时，胎面部分质量开始出现滑动，胎面与路面处于部分粘滞状态，摩擦力逐渐从静摩擦过渡到动摩擦。由于动摩擦力小于最大静摩擦力，因此该部分的曲线斜率为负值。当v>v2时，胎面与地面间完全滑动，摩擦力为动摩擦力。由于相对粘滞阻尼的存在，随着Vr的进一步增大，动摩擦力也会有增大趋势。因此，当轮胎在路面上滚动时，其接地区域时常处于滚、滑状态，即存在弹性滑转现象[7]。

1.2分布式动态摩擦模型选用

经分析，轮胎面-路面构成一个动态的摩擦系统，用静态摩擦模型无法描述摩擦力变化滞后于速度变化。因此引入动态摩擦模型[9-11]，即分布式LuGre摩擦模型。该模型将摩擦的接触面视为微观下具有随机行为的一系列弹性鬃毛，摩擦力由鬃毛弯曲变形产生，一般用中间变量z表示鬃毛的平均变形，模型表达为

(1)

式中：f为LuGre摩擦力；fz为接地压力分布；σ1为鬃毛阻尼系数，可理解为胎面橡胶等效剪切刚度；σ2为相对黏滞阻尼系数，可理解为胎面橡胶阻尼；v为两表面相对滑动速度，即胎面接地区域橡胶与路面的相对滑移速度；fc为库伦摩擦力；fs为最大静摩擦力；vs为Stribeck速度；δ为Stribeck指数(一般取0.5～2)。

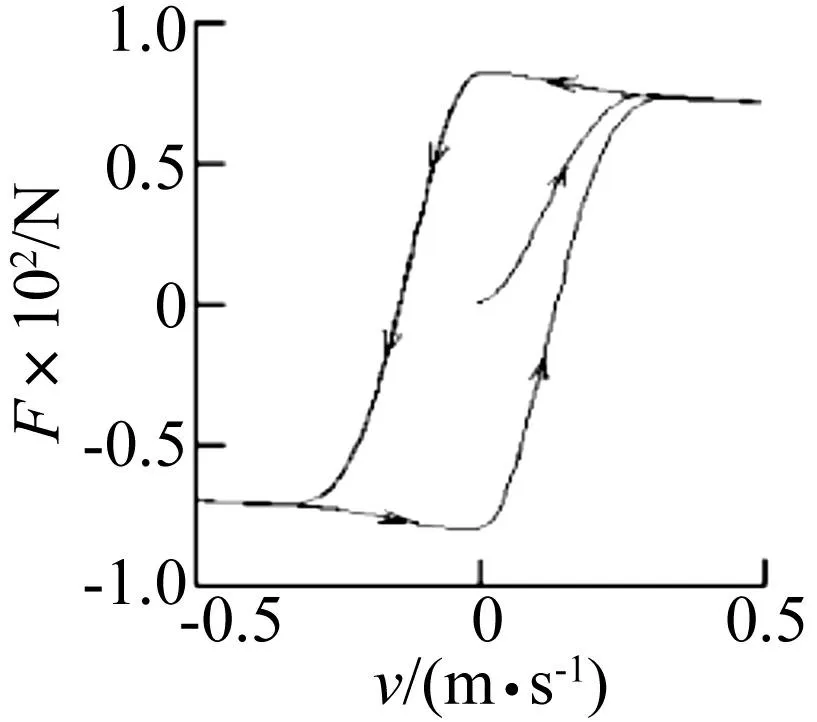
图3　摩擦力“迟滞”现象 Fig.3 “Hysteresis” phenomenon of friction

黄铧等[8]对LuGre模型进行数值仿真发现，相对速度v以一定频率变化时，其摩擦力会表现出明显的“迟滞”现象，且v的变化频率越快，“迟滞”现象越明显，说明LuGre摩擦模型能反映轮胎与路面摩擦的瞬态特性，见图3。

分布式LuGre摩擦模型具有数学形式简洁、参数物理意义明确等优点，便于数值仿真；亦可反映轮胎摩擦力接地印迹纵向的分布规律。因此，本文选该模型描述离散的胎面橡胶摩擦特性。

2胎面纵向振动模型建立

汽车直线行驶时车轮主要沿纵向受力，因此本文仅考虑轮胎面与路面接地区域的橡胶块纵向受力，建立离散化的纵向振动模型。

2.1基本假设提出

(1)研究对象简化。由于只研究轮胎面在纵向的振动特性，因此不考虑沿胎宽的变形；胎基因有钢丝层及帘布层，刚度较胎面橡胶大，故设胎基为刚性。

(2)接地印迹简化。轮胎面具有一定弧度，当受到一定垂载压变形后，轮胎面接地印迹呈现近似矩形的椭圆，因此本文用矩形进行拟合接地印迹。

简化所致误差分析：①以算例所用轮胎为例，估算发现胎基的拉伸刚度远大于胎面橡胶，因此认为不会对计算结果产生明显影响。②胎面接地矩形计算公式据实际试验数据拟合而得，计算所得接地面积、接地长宽误差控制在5%以内，认为该简化对模型准确性影响不大。

2.2理论模型建立

汽车轮胎受到一定载荷后，胎面与路面属于面接触，考虑胎面橡胶具有一定质量及弹性，本文采用弹簧质量系统模拟胎面接地区域的运动情况，见图4。振动模型主要由轮胎与地面组成，轮胎只画出研究目标，即胎基、胎面；胎面橡胶被离散成n个质量块，且沿胎面接地区域均匀分布；质量块间弹簧用于模拟胎面胶之间的挤压效果，ki为挤压刚度；质量块与胎基之间的弹簧用于模拟胎面胶与胎基之间的剪切作用，kie为剪切刚度，ci为橡胶阻尼。

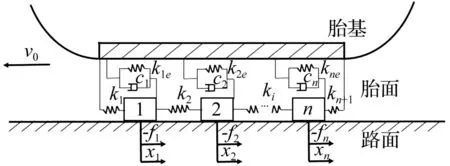
图4　胎面纵向振动模型 Fig.4 Longitudinal vibration model of tread

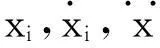
(2)

式中：i=2,3,…,n-1；mi为第i个质量块质量；fi为第i个质量块所受LuGre摩擦力大小。

考虑转矩平衡，车轮整体受力分析见图5，其中Md为制动力矩(也可为驱动力矩，反向)，Ff为胎基所受纵向力之和，FZ为胎面接地压力之和，由于轮胎的迟滞特性，使分布压力有一前移a而产生滚动力矩。建立转矩平衡微分方程为

式中：J为轮胎绕轮心的转动惯量；FZi为第i个质量块所受垂向力；Re为轮胎有效半径。

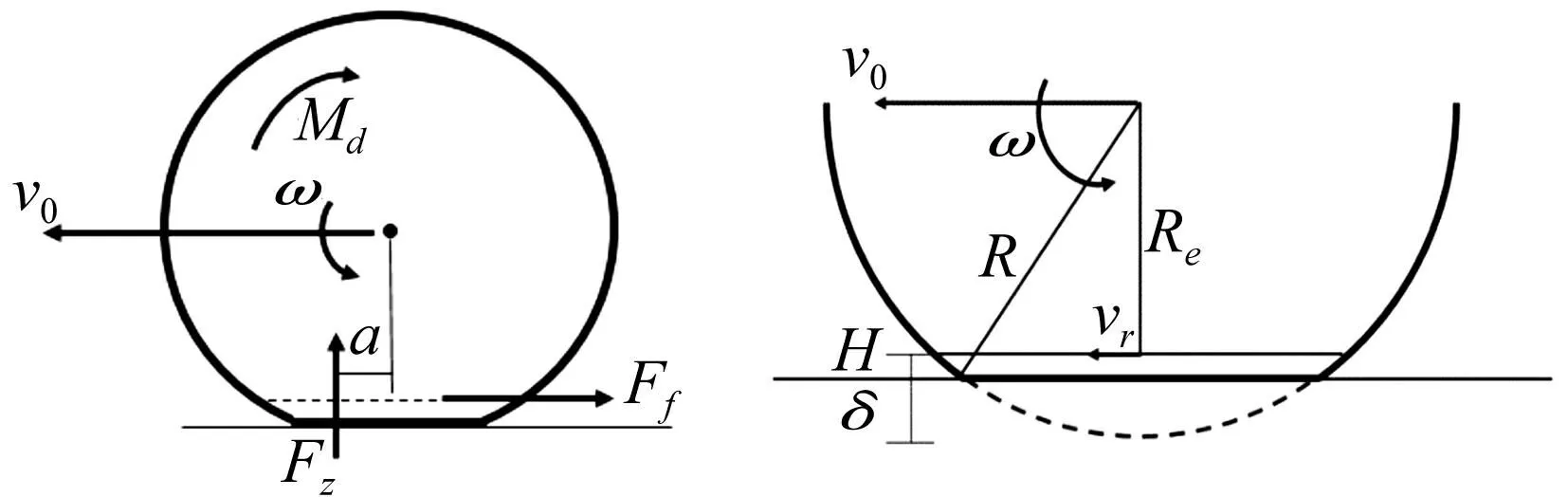
图5 车轮整体受力分析Fig.5Overallforceanalysisofwheel图6 胎基速度示意图Fig.6Schematicoftirebasevelocity

LuGre摩擦力输入速度v为质量块与地面之间的相对速度，即

(4)

式中：vr为胎基相对地面速度，其计算示意图见图6，故有

vr=v0-ωRe

(5)

式中：H为胎面橡胶厚度；δ为轮胎最大下沉量。

联立式(3)、(4)得关于胎面纵向振动的力学模型为

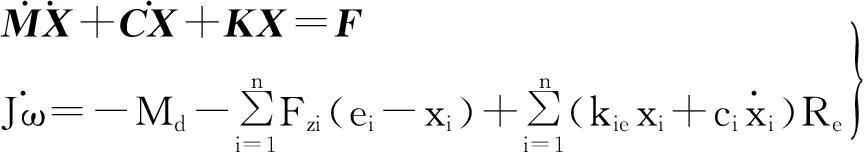
式中：M，C，K为质量、阻尼、刚度矩阵；X，F为水平位移向量及力向量。

2.3参数等效及辨识

2.3.1接地印迹计算

轮胎的接地印迹常采用近似拟合公式计算接地区域等效长宽及面积，即

(7)

式中：s,t为经验系数；B0为胎冠宽度；δ为轮胎最大下沉量，经验公式[7]为

(8)

式中：C1为轮胎设计参数，子午线轮胎取1.5；W为轮胎载荷(10 N)；k0=15×10-3S0+0.42；D为轮胎外径(cm)；S0为轮胎宽度(cm)；p为轮胎内气压(100 kPa)。

然而在实际使用过程中发现该公式误差较大，吴旭东[12]将其与实际测试数据对比进行参数拟合修正，获得适用于轿车轮胎的接地长宽拟合公式，即

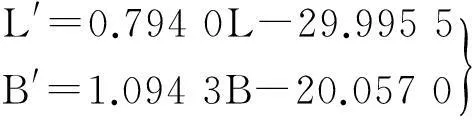
(9)

2.3.2接地压力计算

轮胎在垂直载荷作用下印迹的垂向载荷分布可表示为

(10)

式中：a为接地印迹半长；η(u)为载荷分布函数，u为接地分布系数，为接地区域分布坐标x与接地半长a的比值，即u=x/a，且0≤u≤2。

为保证数值拟合的准确性，本文用四次多项式拟合静态载荷分布函数，即设η(u)=C1u+C2u2+C3u3+C4u4。通过对接地压力数据拟合，获得当前使用工况对应的4个常数C1、C2、C3、C4。

2.3.3表观压缩、剪切刚度计算

王吉忠等[13]据轮胎面单元在典型工况的变形特点，用能量法确定胎面单元变形的位移函数，导出轮胎面单元表观压缩刚度、剪切刚度理论计算式为

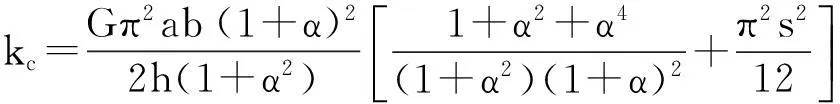
(12)

式中：G为剪切模量；α为长宽比；β为长高比。

3数值模拟

对理论模型阶数n，需针对不同工况下接地花纹块数目确定。本文选165/60 R14的轿车轮胎，据实验，在正常胎压、垂载下，接地区域纵向花纹块数约8块，因此取n=8；对常微分方程(5)的求解，采用状态空间法，利用Matlab/Simulink的State-space模块；再利用Simulink平台搭建仿真模型，对影响胎面附着的各因素进行单因素分析，得到一系列结论。

3.1理论模型状态空间描述

由以上知，可选择状态变量z及输入u，即

(13)

状态方程为

(14)

因此，对应的状态空间系统矩阵A及输入矩阵B分别为

(15)

(16)

如果输出前8个速度项，则对应的输出矩阵为

(17)

如果输出最后1个角速度项，对应的输出矩阵为

(18)

此例中，由于只需输出相关的速度、角速度，故直接矩阵为零矩阵。

3.2Simulink模型搭建

图7为仿真模型流程框图。由图7看出，输入参数后利用两个状态空间模块State-Space1及State-Space2计算获得状态变量及力(矩)，可反馈给状态空间模块影响状态变量输出，形成闭环自平衡体系，获得问题的解。

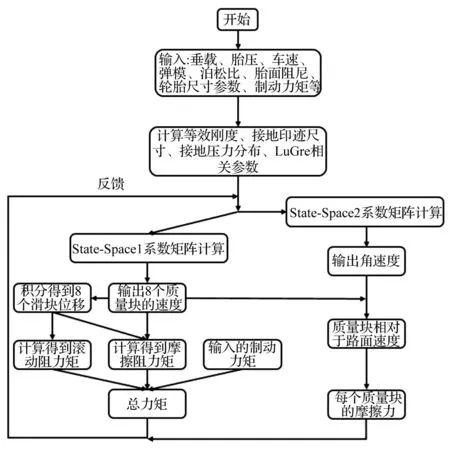
图7　仿真模型流程框图 Fig.7 Flowcharts of simulation model

3.3仿真结果分析

考虑各参数及结构参数变化对轮胎整体附着特性影响，对比已有结论验证模型的正确性；通过分析获得胎面接地区域摩擦力、附着力等分布情况。仿真分析针对的系统均为之前的理论模型，且每次仅对单一因素进行影响分析。

3.3.1结构、使用参数对胎面附着特性影响分析

完全刚性轮胎在刚性路面上滚动时不会产生滚动阻力；一般情况下，由于普通轮胎自身材料特性引起的弹性迟滞损失及软路面变形沉陷，对轮胎的垂向反力总向前产生偏移距a，而产生一定滚阻力矩[14]，并通过轮胎纵向摩擦力产生的力矩进行平衡。因此滚阻系数可作为反映胎面附着特性的重要指标，大小受轮胎结构参数影响。

据图5，滚阻系数μr的计算式为

(19)

3.3.1.1车轮直径影响分析

图8为轮辋半径对滚阻系数影响。由图8看出，随轮胎半径从27.68 cm增加到35.03 cm(图中从17.8 cm增加到25.4 cm)时，轮胎的滚动阻力系数随之下降，并呈一定线性下降趋势。

3.3.1.2胎面材料参数影响分析

对常见的轮胎面弹性模量变化范围(3～10 MPa)，选15个点进行仿真计算，所得结果见图9。由图9看出，等效弹模对滚阻系数影响呈一定规律，当胎面橡胶弹性模量从3～10 MPa变化时，滚动阻力系数逐渐下降，但并不明显，处在0.025～0.026范围内。表明胎面橡胶越硬，接地区域产生的滚动阻力矩越小，但对滚阻系数影响不明显。

3.3.1.3胎压变化影响分析

轮胎胎压影响轮胎的弹性及缓冲性能，胎压对滚阻系数影响见图10。由图10看出，当胎压适当提高(小于0.3 MPa)时，轮胎的滚动阻力系数下降较快；胎压继续增加时滚阻系数减小缓慢。

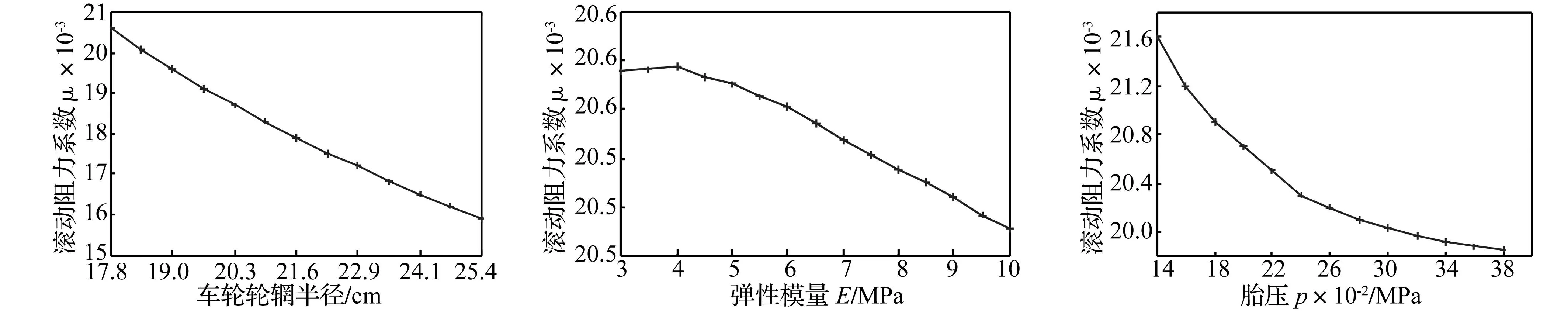
图8 轮辋半径对滚阻系数影响Fig.8Theeffectofrimradiusonrollingresistancecoefficient图9 胎面胶等效弹模对滚阻系数影响Fig.9Theeffectofequivalentelasticmodulusonrollingresistancecoefficient图10 胎压对滚阻系数影响Fig.10Theeffectoftirepressureonrollingresistancecoefficient

3.3.1.4轮胎制动力矩影响分析

制动力矩增加，会使与之平衡的纵向摩擦力矩相应增加，见图11。由图11看出，增加制动力矩，滚阻系数呈线性增加趋势。为使力矩平衡，轮胎纵向抵消制动力矩的摩擦力增大，致滚阻系数不断增大。

通过对模型参数调整，对比分析获得车轮结构参数(车轮半径、胎面材料特性)及使用参数(胎压、垂载)对轮胎滚阻系数影响，所得规律与文献[14]吻合。

3.3.2胎面接地区域附着特性分布规律分析

轮胎因自身变形与路面为面接触，接地区域的附着特性具有一定分布规律，传统的点接触模型由于假设缺陷不能反映此规律。而本模型针对胎面接地区域的离散化，可反映车轮滚动时的摩擦分布规律。

由于轮胎的弹性迟滞，地面对其垂向反力并非前后对称分布，即总向前偏移一定距离a，因此峰值附着力的分布也类似，见图12，可见附着力分布呈中间大两头小趋势，而峰值向前偏移出现于第三滑块处。由摩擦力分布也发现分布在前3/4区域的摩擦力明显大于后1/4区域，说明接地胎面的纵向摩擦力并非均匀分布，3/4区域与地面接触产生80%以上的摩擦力，而后部分因位移较大，胎面橡胶与地面已产生相对滑动，因此摩擦力相对较小。第1、8两滑块所受摩擦力较小，此因分布于首尾两区域的垂向力较小所致。

对模型施加较大转矩时该工况下各质量块相对胎基振动稳定时位移见图13。由图13看出，自前向后(车轮前进方向为前)质量块滑移位移呈现较明显的上升趋势，说明胎面接地区域后部位移大于前部，即接地区域胎面橡胶变形从前往后趋于明显。然而因变形过大突破最大摩擦力时，大位移会变成相对滑动。结合图12看出，最后两滑块产生的摩擦力较小，即为胎面橡胶在接地区域后端由于变形过大产生相对滑动引起的。滑块1的位移较滑块2大的原因为模型接地前端刚度约束偏小，使滑块1的位移偏大，但对结果影响不明显。

图11 制动力矩对滚阻系数的影响Fig.11Theeffectofbrakingtorqueonrollingresistancecoefficient图12 胎面附着力及摩擦力分布图Fig.12Distributionoftreadadhesionandfriction图13 各质量块稳定位移分布图Fig.13Stabledistributionofeachmass’sdisplacement

4结论

本文针对某轮胎在突加(制动或驱动)转矩情况，建立离散化纵向振动模型，并进行数值计算。通过对模型参数调整，分析获得车轮结构、使用参数对胎面附着特性的影响规律及胎面纵向摩擦力与位移的分布规律。结论如下：

(1)车轮滚动时，胎面-路面摩擦力在接地区域呈一定分布规律，前部大后部小；随摩擦力增加在接地区后端率先突破附着而产生相对滑移。

(2)沿纵向接地区，轮胎面位移自前向后逐渐增加，胎面橡胶变形亦越明显。从胎面块纵向振动角度解释了轮胎滚动状态下胎面橡胶的变形规律，并验证模型的正确性。

(3)将胎面的离散化与分布式LuGre摩擦模型结合用于胎面纵向振动分析，可通过输入不同工况参数实现胎面接地区域的附着力分布特点及动态变化描述。

参考文献

[1]Savkoor A R. On the friction of rubber[J]. Wear, 1965, 8(3): 222-237.

[2]李勇,左曙光,雷镭,等.基于LuGre摩擦模型的轮胎多边形磨损机理分析[J]. 振动与冲击, 2010,29(9):108-112.

LI Yong, ZUO Shu-guang, LEI Lei, et al.Analysis on polygonal wear of automotive tire based on LuGre friction model[J]. Journal of Vibration and Shock, 2010,29(9): 108-112.

[3]李勇,左曙光,雷镭,等.基于胎面侧向振动的轮胎多边形磨损机理分析[J]. 同济大学学报(自然科学版), 2011, 39(1): 100-104.

LI Yong, ZUO Shu-guang, LEI Lei, et al. Analysis onpolygonal wear of automotive tire based on lateral vibration of tire tread[J]. Journal of Tongji University(Natural Science), 2011, 39(1): 100-104.

[4]刘昭度. 轮胎-路面纵向附着动力学数学模型[J]. 北京理工大学学报(英文版), 1996(2): 193-204.

LIU Zhao-du. Mathematical models of tire-longitudinal road adhesion and their use in the study of road vehicle dynamics[J]. Journal of Beijing Institute of Technology (English Edition), 1996(2): 193-204.

[5]庄晔. 轮胎动摩擦特性研究及其对车辆操纵稳定性的影响[D]. 长春: 吉林大学, 2004.

[6]吴广政. 轮胎纵向附着特性数学模型[J]. 北京汽车, 2000(6): 1-4.

WU Guang-zheng. Mathematical model of tire longitudinal adhesion properties[J]. Beijing Automotive Engineering, 2000(6): 1-4.

[7]庄继德.汽车轮胎学[M]. 北京:北京理工大学出版社, 1996.

[8]黄铧,左曙光,杨宪武,等.基于LuGre摩擦模型的轮胎自振系统数值分析[J]. 计算机辅助工程, 2009,18(4):19-23.

HUANG Hua, ZUO Shu-guang, YANG Xian-wu, et al. Numerical analysis on self-excited vibration system of tire based on LuGre friction model[J]. Computer Aided Engineering, 2009,18(4):19-23.

[9]Canudas-de-Wit C, Olsson H, Astrom K J, et al. A new model for control of systems with friction[J]. Automatic Control, IEEE Transactions on, 1995, 40(3): 419-425.

[10]Canudas-de-Wit C, Tsiotras P. Dynamic friction models for road-tire longitudinal interaction[J]. Vehicle System Dynamics: International Journal of Vehicle Mechanics and Mobility, 2003, 39(3):189-226.

[11]张鹏,张明,夏群生,等.基于LuGre摩擦模型的轮胎稳态模型参数识别[J]. 农业机械学报, 2008,39(5):204-207.

ZHANG Peng, ZHANG Ming, XIA Qun-sheng, et al. Parameter identification of tire steady-state model tire based on LuGre friction model[J]. Transactions of the Chinese Society for Agricultural Machinery, 2008, 39(5):204-207.

[12]吴旭东. 基于悬架-轮胎系统的轮胎多边形磨损研究[D]. 上海: 同济大学, 2011.

[13]王吉忠, 庄继德. 轮胎胎面单元表观刚度计算[J]. 农业工程学报, 2000, 16(2): 28-31.

WANG Ji-zhong, ZHUANG Ji-de. Calculation of the apparent stiffness of tyre tread element[J]. Transactions of the Chinese Society of Agricultural Engineering, 2000, 16(2): 28-31.

[14]吴光强. 汽车理论[M]. 北京: 人民交通出版社, 2007: 3-14.