Banach空间中混合均衡问题和相对拟非扩张半群公共解的一种逼近方法
2015-12-29李秀仁王晶海
李秀仁,王晶海
(福州大学数学与计算机科学学院,福建福州 350116)
0 引言
混合均衡问题是一类十分广泛的均衡问题,它在非线性分析领域有着重要理论和应用价值.非线性分析领域中的许多问题都可以纳入混合均衡问题的框架中加以研究,例如一般均衡问题、变分不等式问题、最优化问题和Nash均衡问题都是其特殊的情形.
设E为Banach空间,C为E的非空闭凸子集.设θ:C×C→R是一个均衡二元函数,即对任意的u∈C,θ(u,u)=0,φ:C→R是一个实值函数,混合均衡问题是求x∈C,使得MEP:θ(x,y)+φ(y)-φ(x)≥0,∀y∈C.记Ω为混合均衡问题MEP(θ,φ)的解集.
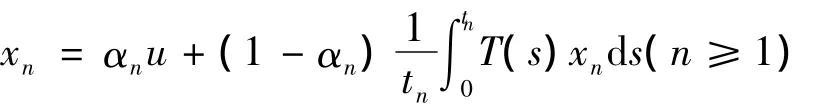
由于混合均衡问题具有广泛的应用,因而备受学者们的青睐.Fan L Y[1]在Hilbert空间中研究了混合均衡问题的解的存在性;Ceng等[2]通过使用KKM技术,得到混合均衡辅助问题的解的存在性和唯一性;文献[3-5]分别用不同迭代方法讨论并得到解的强收敛定理;Shioji等[6]在Hilbert空间中利用隐迭代,证明了在适当条件下序列{xn}强收敛于非扩张半群的不动点集中的一点;Suzuki[7]在Hilbert空间非扩张半群上利用隐迭代xn=αnu+(1-αn)T(tn)(xn)(n≥1),证明了在适当条件下序列{xn}的强收敛性;2005年,Xu[8]将文献[7]的结论推广到具有弱连续的对偶映射的一致凸的Banach空间上;之后,Aleyner等[9]首次在一致光滑的Banach空间上利用显迭代xn+1=αnu+(1-αn)T(tn)(xn),n≥0,x0∈C,证明了在适当条件下序列{xn}的强收敛性;2007年,张石生等[10]在Banach空间上引入了一种新的非扩张半群的显式复合迭代方法,并证明了其在适当条件下的强收敛性;2010年,唐金芳[11]在Hilbert空间中引进并研究了一种新的迭代算法,借以寻求混合均衡问题解集与非扩张半群不动点集的公共元;2011年,Ceng和Guu[12]在一致光滑和一致凸的Banach空间上建立一种求解广义均衡问题和一族可数的相对非扩张映射不动点问题及极大单调算子的公共解的混合收缩投影算法;2012年,马乐荣等[13]在Hilbert空间中,设计了两种新的关于Meir-Keeler压缩映像的粘滞型迭代算法,用以逼近非扩张半群的公共不动点,在适当的条件下,利用所提出的算法证明了非扩张半群公共不动点的强收敛定理;同年,Chang等[14]在Banach空间的框架下,借助修正的Halpern-Mann迭代算法,求解全局渐进拟φ非扩张半群的解集,并在适当的条件下,证明了该迭代序列的强收敛性;近来,Wattanawitoon[15]在Banach空间中通过一种混合投影算法寻求均衡问题和两个相对拟非扩张映射的不动点,使研究的范畴更广泛;2011年,Cholamjiak和Suantai[16]在Banach空间中,建立了逼近混合均衡问题和一可数族非扩张映射的公共解的迭代算法,并证明了算法的强收敛和弱收敛定理.
本文在Banach空间中,通过建立一种新的迭代算法,研究混合均衡和相对拟非扩张半群的不动点的公共解问题,得到该算法所产生的迭代序列的强收敛定理.
1 预备知识
为解出混合均衡问题,假设二元函数θ满足下列条件:
(A1)θ(x,x)=0(∀x∈ C);
(A2)θ为单调的,即θ(x,y)+θ(y,x)≤0(∀x,y∈C);
(A3)θ(x,y)关于第一变量x为弱上半连续;
(A4)θ(x,y)关于第二变量y为凸和下半连续.
设U={x∈E:x=1}为E的单位球.称Banach空间E为严格凸的如果对所有x,y∈U,x≠y有
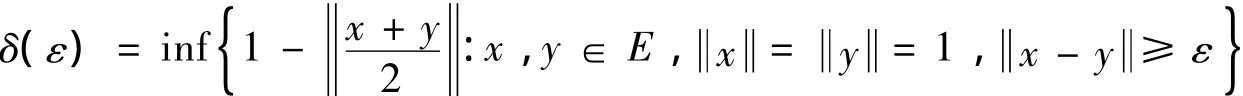
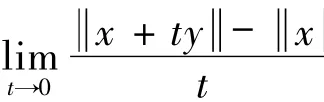
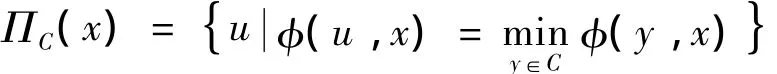
易见,若E为Hilbert空间,则φ(x,y)= x-y2,∀x,y∈H,且广义投影算子ΠC就是通常的投影算子.广义投影算子ΠC的存在性和唯一性可参考文献[16-19].同时从函数φ(x,y)的定义可得
1)(y - x)2≤ φ(y,x)≤(y+x)2,∀x,y∈E;
2)φ(x,y)= φ(x,z)+ φ(z,y)+2〈x - z,Jz- Jy〉,∀x,y,z∈E;
3)若E为一致凸和光滑的Banach空间,对所有x,y∈E有φ(x,y)=0当且仅当x=y;
4)φ(x,y)=〈x,Jx-Jy〉+〈y-x,Jy〉≤ x Jx-Jy+ y-x y,∀x,y∈E.
设E*为E的对偶空间,C⊂E,T:C→C,若 Tx-Ty≤ x-y,∀x,y∈C则称映射T为非扩张.点x∈C使得Tx=x则称x为T的不动点.用F(T)表示T的不动点集,即F(T)={x∈C:Tx=x}.若C中有一序列{xn}且该序列弱收敛于点ω∈C使得极限xn-Txn=0,则称点ω是T的渐近不动点.用(T)表示T的渐近不动点集.称T为相对非扩张的,若(T)=F(T)且对所有点x∈C及ω∈F(T)有φ(ω,Tx)≤φ(ω,x).称T为φ-非扩张的,若对任意x,y∈C有φ(Tx,Ty)≤φ(x,y).称T为相对拟非扩张的,如果F(T)≠Φ且对任意的x∈C,ω∈F(T)有φ(ω,Tx)≤φ(ω,x).称T为稳定非扩张(firmly-nonexpansive),若对所有的x,y∈E有

设C为E的非空闭凸子集,一族映射{T(t):C→C,t≥0},称该族映射为C上的相对拟非扩张半群.如果以下条件满足:
1)对任意的t1,t2∈R+,x∈C有T(t1+t2)x=T(t1)T(t2)x;
2)对任意的x∈C有T(0)x=x;
3)对任意的x∈C有t|→T(t)x是连续的;
4)F≠Φ,且对任意的t∈R+,x∈C,ω∈F有φ(ω,T(t)x)≤φ(ω,x).其中:F:={x∈E:T(t)x=x,t≥0}=∩t≥0F(T(t))为映射族{T(t):C→C,t≥0}的公共不动点集.
引理1[16]设C为光滑的一致凸的Banach空间的非空有界闭凸子集,θ:C×C→R是一个均衡二元函数且满足上述(A1)-(A4)条件,φ:C→R是一个实值函数且为凸下半连续.对任意r>0,x∈E,定义映射Sr:E→2C:
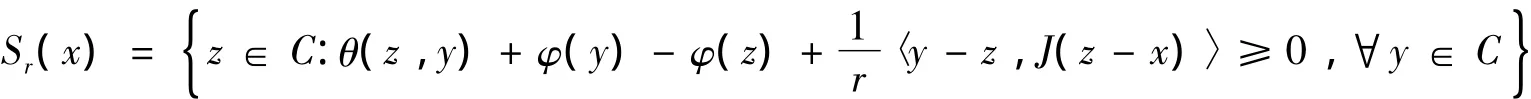
则下述情况都成立:
1)对每个x∈E,Sr(x)≠Φ;
2)Sr是单值的;
3)〈Srx-Sry,J(Srx-x)〉≤〈Srx-Sry,J(Sry-y)〉,对任意x,y∈E;
4)F(Sr)=MEP(θ,φ);
5)MEP(θ,φ)是非空闭凸的.
引理2[20]设C为光滑的一致凸的Banach空间的闭凸子集,θ:C×C→R是一个均衡二元函数且满足上述(A1)-(A4)条件,φ:C→R是一个实值函数,r>0.如果Sr为稳定非扩张,则对x∈E,ω∈F(Sr)有
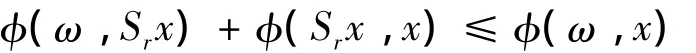
引理3[21]设C为光滑的Banach空间的非空闭凸子集,x∈E,则x0=ΠCx当且仅当〈x0-y,Jx-Jx0〉≥0,∀y∈ C.
引理4[21]设E为自反,严格凸和光滑的Banach空间,C为E的非空闭凸子集,x∈E,则φ(y,ΠCx)+φ(ΠCx,x)≤ φ(y,x),∀y∈C.
引理5[22]设E为一致凸和光滑的Banach空间,{xn},{yn}为E中两个序列,若φ(xn,yn)→0,且{xn}有界或{yn}有界,则xn-yn→0.
引理6[23]设E为一致凸和光滑的Banach空间,C为E的闭凸子集,T:C→C为闭的相对拟非扩张映射,则F(T)为C的闭凸子集.
引理7[24]设E为一致凸的Banach空间,Br(0)为E的闭球,则存在一个连续严格递增凸的泛函g:[0,∞)→[0,∞),g(0)=0,使得对任意x,y∈Br(0)有
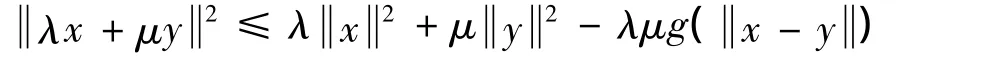
其中:λ,μ∈[0,1]且 λ+μ =1.
引理8[22]设E为光滑一致凸的Banach空间,r>0,则存在一个严格递增连续且凸的泛函g:[0,2r]→R,使得g(0)=0,且对任意x,y∈Br(0)有g(x-y)≤φ(x,y).
引理9[25]设E*为一致凸的Banach空间,J为E的对偶映射,则J为单值的且在E的有界子集上一致连续,即B为E的有界子集,ε>0,存在δ>0,使得对任意x,y∈B, x-y <δ,有 J(x)-J(y) <ε.
2 主要结果
定理1 设E为一致光滑和一致凸的Banach空间,C为E的非空闭凸子集,θ:C×C→R是一个均衡二元函数且满足上述(A1)-(A4)条件,φ:C→R为凸下半连续实值函数,W ={T(t):t≥0}为E中相对拟非扩张半群.设{xn},{yn},{zn},{un}四个序列如下定义:
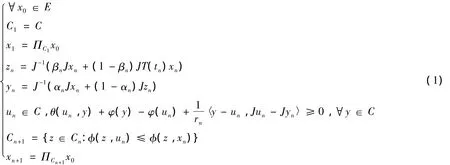
其中:J为E的正规对偶映射,un=Srnyn,序列{αn},{βn}⊂(0,1),对某个a>0,有{rn}⊂[a,∞),{tn}⊂[0,∞)为递增且tn=∞.如果对rn>0,Srn为稳定非扩张,且Γ:=F()∩MEP(θ,φ)=F(T(t))∩Ω≠Φ,那么序列{xn},{un}强收敛于ω∈Γ,其中ω =ΠΓx0.
证明 分以下六步骤完成定理的证明.
第一步,证明对任意的n≥0,Cn是闭凸集.显然C1=C是闭凸的,假设对某个k∈N,Ck是闭凸的,对于z∈ Ck使得φ(z,uk)≤φ(z,xk),其等价于2(〈z,Jxk〉-〈z,Juk〉)≤ xk2- uk2,可得 Ck+1是闭凸的.因此对所有的n≥0,Cn是闭凸集,这表明ΠCn+1x0是有定义的.
第二步,证明对任意的n≥0,Γ⊂Cn.显见Γ⊂C1=C,假设对某个k∈N,Γ⊂Ck,则对任意的p∈Γ⊂Ck有:
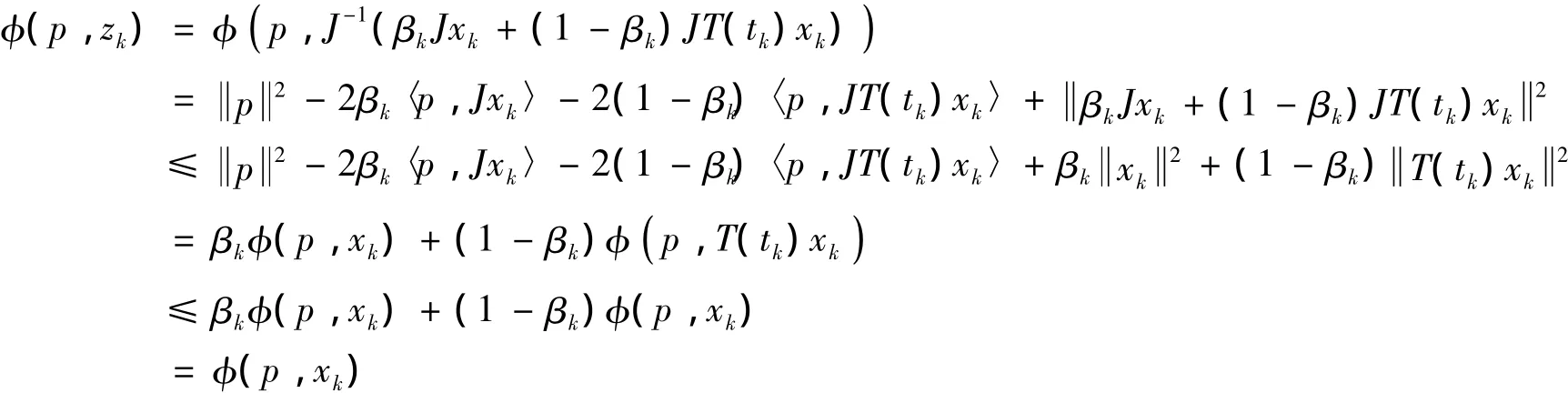
及
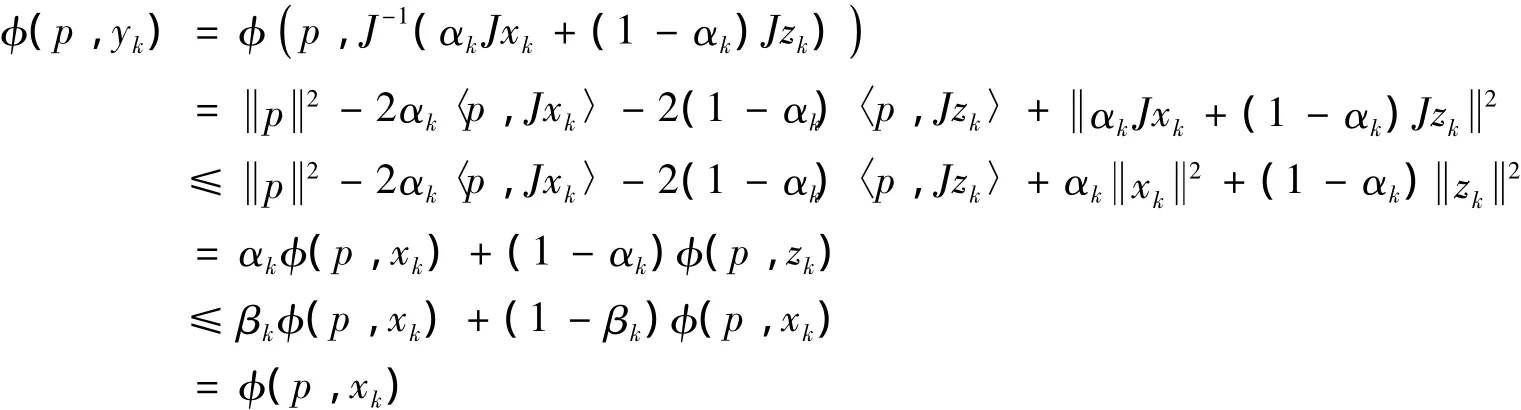
由引理2可知,若Srn为稳定非扩张,则Srn为相对拟非扩张,考虑un=Srnyn,有φ(p,uk)=φ(p,Srkyk)≤φ(p,yk)≤ φ(p,xk),即 p∈ Ck+1.因此,Γ ⊂Cnn=0,1,2,….
第三步,证明{xn}为Cauchy列.由xn=ΠCnx0,则对任意z∈Cn,p∈Γ,有〈xn-z,Jx0-Jxn〉≥0及〈xn-p,Jx0-Jxn〉≥0.由引理4,当n≥1有 φ(xn,x0)= φ(ΠCnx0,x0)≤φ(p,x0)-φ(p,xn)≤φ(p,x0),因此序列{φ(xn,x0)}有界.由xn= ΠCnx0,有φ(xn,x0)≤φ(xn+1,x0),则序列{φ(xn,x0)}非递减数列,从而φ(xn,x0)存在.由Cn的结构知,对任意正整数m≥n,有Cm⊂Cn,xm=ΠCmx0∈Cn,则 φ(xm,xn)= φ(xm,ΠCnx0)≤φ(xm,x0)-φ(ΠCnx0,x0)= φ(xm,x0)-φ(xn,x0),令m,n→0有φ(xm,xn)→0.根据引理5可得,当m,n→0有xm-xn→0.由此可见,{xn}为Cauchy列.设xn→ω∈C.

移项可得(1-αn)βn(1-βn)g(JT(tn)xn-Jxn)≤φ(p,xn)-φ(p,un).另一方面有:
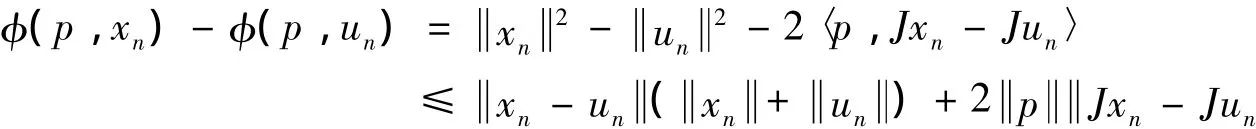
第五步,证明ω∈MEP(θ,φ)=Ω =F(Sr).由Cn的结构可知φ(z,un)≤φ(z,xn),又因un=Srnyn和引理2可得:
φ(un,yn)= φ(Srnyn,yn)≤φ(p,yn)- φ(p,Srnyn)≤φ(p,xn)- φ(p,Srnyn)= φ(p,xn)- φ(p,un)当n→∞ 时φ(p,xn)-φ(p,un)→0,所以当n→∞ 时φ(un,yn)→0.由引理5得yn- un=0,所以Jyn-Jun=0,从而,.另外,u=Sy有 θ(u,y)+φ(y)- φ(u)+
nrnnnn〈y-un,Jun-Jyn〉≥0,∀y∈C,由于θ的单调性和φ的下半连续性,注意到
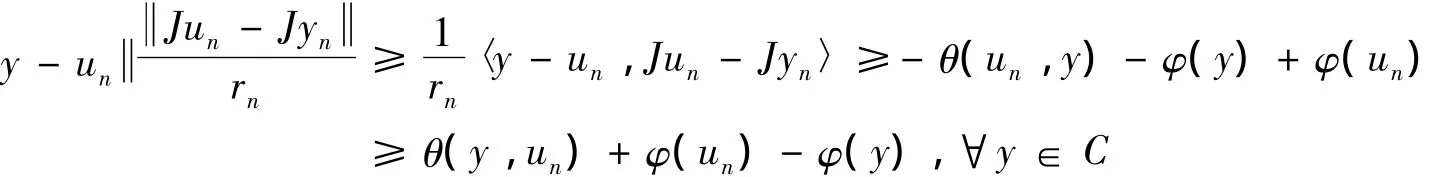
当n→∞ 时,un→ω,θ(x,y)关于第二变量凸下半连续性,所以θ(y,ω)+φ(ω)-φ(y)≤0,即θ(ω,y)+φ(y)≥φ(ω),∀y∈C,则可得ω∈MEP(θ,φ)=Ω =F(Sr).综上可知ω∈Γ.
第六步,证明ω =ΠΓx0.因xn=ΠCnx0,对所有的z∈Cn,有〈xn-z,Jx0-Jxn〉≥0且对任意的p∈ Γ,有〈xn-p,Jx0-Jxn〉≥0,则可知〈ω -p,Jx0-Jω〉≥0,∀p∈Γ,再根据引理3可得ω =ΠΓx0.
综上所述,定理1证明完毕.
