基于数据挖掘的大学生心理问题分析
2015-12-29郭晶晶
基于数据挖掘的大学生心理问题分析
郭晶晶
(淮北职业技术学院 计算机科学技术系,安徽 淮北235000)
摘要:大学生群体面对的来自学习、社会环境、人际关系等方面的压力很大,容易产生多种心理问题。本文在大学生心理健康综合模糊判定系统基础上,利用最大隶属度原则,为有心理问题的压力很大的学生寻找影响其心理健康的因素,为大学生心理健康工作提供技术支持。
关键词:大学生;心理健康;模糊综合判定;最大隶属度原则
收稿日期:2015-03-27
作者简介:郭晶晶(1984-)女,安徽淮北人,淮北职业技术学院计算机科学技术系助教,研究方向为计算机应用技术。
中图分类号:G446
各高校都越来越关注大学生心理健康教育的问题。大部分专家学者是采用量表对心理健康问题进行研究。[1]为满足高校需求,应开发一个心理健康评价系统,按该测评系统指导高校心理健康决策者,对学生进行个性化的人才培养。同时这也有利于各企业客观、可靠地识别、选拔和聘用人才。笔者采用模糊综合评判方法,以期为我国大学生心理健康测评体系的构建提供技术支持。
1相关技术
1.1数据挖掘技术
随着数据库技术的成熟和信息化数据的普及应用,社会心理学研究所能利用的数据也随之积累并迅速扩大,这使得在心理健康领域使用数据挖掘技术有了可能。当前使用的心理学领域的数据挖掘算法有两个,一个是决策树:该算法可以分析数据,预测心理问题和行为。二是关联规则:可以通过其找出原因及其对造成某种心理现象的影响程度,确定属性之间的关系为进一步的研究提供参考。[2]
1.2模糊综合评判技术
美国自动控制专家扎德(L.A.Zadeh)于1965年发表了题为《Fuzzy Sets》的论文,宣告模糊数学的诞生。[3]模糊数学原理就是试图用数学工具解决模糊事物方面的问题。而模糊综合评价就是以此为基础,将一些模糊、难以确定的因素定量化,多方面多角度综合性地对被评价事物隶属等级进行评价的一种方法。鉴于心理健康是一个模糊的概念,模糊综合评价方法可以用来建立一个心理健康的模糊综合评价模型,并给出一系列心理健康评估。
1.3最大隶属度原则
1965年,美国控制论教授扎德(L.A Zadeh)发表了名为《模糊集》的论文。他在里面详细阐述了模糊评价函数里的隶属度概念。与此相关的,被评价事物对各等级模糊子集的隶属度构成的评判向量所遵循的原则即为最大隶属度原则。
2心理测评体系构建
2.1数据准备
笔者向本人所在学校的10个专业学生发放匿名调查问卷。问卷的第一部分为选择填空题,大学生对自身心理健康状况作出评价。第二部分为开放式问题,由大学生自由回答这部分提出的心理健康问题,不做限制。然后采用分层抽样的方法抽取学生问卷,共收集到有效问卷410份。
2.2数据分析
通过分析问卷结果得出,大学生认为影响心理健康的因素分别是:压力大(27.2%)、是否受挫折(15%)、人际关系好坏(12%)、家庭条件(9.5%)、恋情 (8.7%)、学习态度(8.2%)、顺利程度(8.2%)、恋爱失败(6.3%)、遭遇挫折(5.3%)、考试(5.1%)、成绩优异(5.1%)、做事是否成功(4%)、朋友多少 (4.0%)、睡眠状况(2.7%)、学习氛围(2.1%)等,这15个影响因素词频总数为587次。
心理健康所涉及的范畴包括学业问题(36%)、生活条件(27.%)、人际关系问题(21.%)、家庭情况(10.2%)以及身体状况(4.%),大学生们选择的这5个范畴词频总数为431次。
2.3模型定义
鉴于上述的调查结果以及心理学专家给出的数据采用加权平均的方法进行处理,我们定义模型如下:
(1) 它们构成的因素集为:U={人际关系,自我评价,社会适应,情绪,人格,意志}。
记为:={u1,u2,u3,u4,u5,u6}
评定论域为:V={ 社会环境,心理健康教育,学业,家庭经济情况,恋爱,就业}。
记为:V={v1,v2,v3,v4,v5,v6}
(1)用ai(i=1…6)表示ui(i=1…6)在大学生心理健康中的模糊权重,得到其模糊权向量为:A=ai=(0.17,0.16,0.17, 0.15,0.17,0.18).
公式①
(2)r1i(i=1,…,6)用来表示vi(i=1,…,6)对u1的影响量,其模糊权向量用R/u1表示;
(3)R/u1=(r11,r12,r13,r14,r15,r16)=(0.17,0.14,0.18,0.15,0.18,0.18)
公式②
(4)rij(i=2,…,6;j=1,…,6)用来表示vj(j=1,…,6)对ui(i=2,…,6)的影响量,其模糊权向量分别用R/u2,R/u3,R/u4,R/u5,R/u6表示,即:
R/u2=(r21,r22,r23,r24,r25,r26)=(0.16,0.13,0.19,0.19,0.15,0.18),
R/u3=(r31,r32,r33,r34,r35,r36)=(0.17,0.17,0.18,0.17,0.14,0.17),
R/u4=(r41,r42,r43,r44,r45,r46)=(0.17,0.16,0.19,0.15,0.16,0.17),
R/u5=(r51,r52,r53,r54,r55,r56)=(0.19,0.16,0.16,0.15,0.16,0.18),
R/u6=(r61,r62,r63,r64,r65,r66)=(0.18,0.16,0.16,0.17,0.14,0.19)。
进而得到其模糊关系矩阵为:
采用M(·,+)算子得到大学生心理健康的模糊综合评价结果向量为:
b=(b1,b2,b3,b4,b5,b6)=A·R=(0.120,0.106,0.115,0.101,0.103,0.125 )。
其中(b1,b2,b3,b4,b5,b6)代表评定论域对大学生心理健康影响的大小,

j=1,2,3,4,5,6
(1)
然而,对于大学生心理健康的评判,直接应用以上得到的模糊综合评价结果向量是不科学的。为了在此基础上更方便的测试每位大学生的心理健康状况,不妨用“1~6”依次表示)(v1,v2,v3,v4,v5,v6)的秩。利用加权平均原则,即
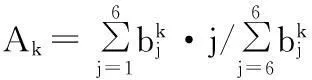
(2)
可得:Ak=2=(1×0.1202+2×0.1062+3×0.1152+4×0.1012+5×0.1032+6×0.1252)/(0.1202+0.1062+0.1152+0.1012+0.1032+0.1052)=3.50。
(3)
式(3)表明: 填写此调查表的心理健康的大学生,按照本文的计算方法算出的最后得分应该是3.50附近的数值。
2.4模型精化
虽然通过计算已得到了心理健康的大学生填写此调查表后得分的参考值点,但我们需要找到一个合理的评定区间,使此评判方法更为科学实用。为此,我们再次随机从调查表中抽出200份,把它们平均分成20组,每组都按照上面的方法算出每一份调查表的最后得分,利用公式再求出每组调查表的最后得分的数学期望,结果分别是:
3.40,3.42,3.54,3.30,3.49,3.56,3.66,3.41,3.26,3.52,3.56,3.67,3.53,3.49,3.52,3.47,3.56,3.60,3.46,3.50.
可见,以上20个数学期望中有17个即85%,落入区间Q1=(3.50×0.97,3.50×1.03)=(3.325,3.605);有2个即10%,落入区间Q2=(3.56×0.95,3.56×1.05)=(3.325,3.675)。还有1个即5%落入区间Q3。因此,我们则可把Q1,Q2,Q3分别认为是心理健康、心理亚健康和心理不健康区间。
2.5预测模型定义
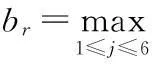
由于使用最大隶属度原则是需要有一定条件的,所以对于其的有效性问题,则要再探讨一下。
首先记:
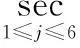
再由β和γ定义β′和γ′,
则β′∈[0,1],γ′∈[0,1]
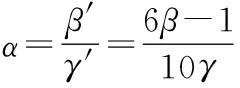
由上式知道,α越大,最大隶属度原则有效性就越高。因此,就用α来度量最大隶属度原则的有效性。结合探讨结果,下面给出了用α对应最大隶属度原则的有效性情况。
当α≥0.2时,我们就可以用最大隶属度原则来寻找导致某同学心理健康处于该区间的原因。反之,若α<0.2时,最大隶属度原则就不适用了。
3结语
笔者针对当前大学生心理健康状况,以期为构建以模糊综合评判为核心思想的大学生心理健康评价体系提供了更好的技术支持,同时也使高校开展心理健康教育工作测量结果更加科学化、客观化。
参考文献:
[1]兰宏勇,化存才,杨俊.贫困大学生心理问题的模糊综合评判模型[D].云南:云南大学,2008.
[2]刘同明,等.数据挖掘技术及其应用[M].北京:国防大学出版社,2001.
[3]张修文,王国俊,刘旺金,模糊数学引论[M].西安:西安交通大学出版社,1991.
责任编辑:万方
