低功耗振荡器设计

华中科技大学 杨 景 曾 强 高一凡

低功耗振荡器设计

华中科技大学 杨 景 曾 强 高一凡

在小型化可穿戴电子产品中，晶体振荡器作为SOC参考时钟占有很大的空间体积，如果设计高精度VCO,可以省去晶体空间体积，降低成本及晶体参考时钟部分电路功耗。本设计用改进的补偿模块降低频率稳定性受PVT变化的影响，采用华润上华0．35umCMOS工艺，在华大九天Aether平台上实现了一个中心频率为433．92MHz的低功耗高精度振荡器。

环形振荡器；低功耗；频率补偿

根据设计目标，我们使用带隙基准电路提供PTAT偏置电流，通过补偿模块提供控制电压给VCO模块，使得振荡器达到较为稳定的工作频率。

图1 整体结构图

带隙模块负责提供PTAT的电流基准，从而利用电流镜镜像的方式提供各支路的偏置电流，同时该电流与绝对温度成正比，当温度升高时，VCO模块的偏置电流增大，使得振荡频率升高，当温度降低时，则使得振荡频率降低，因此，可以起到一定程度上的频率补偿作用。而电路的核心VCO模块要有较好的线性度，适当的中心频率以及宽的频率调节范围。根据巴克豪森准则，要使电路起振，整个电路的环路增益H(jw)必须满足：

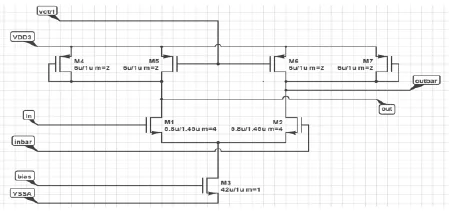
图2 VCO中的单级放大器

以下是经过推导的该VCO的频率和低频增益的表达式：差分延时单元每级延时：

振荡频率：

每级VCO的低频增益Av满足：

差分延时单元与单端输入输出的缓冲级比，差分缓冲级输出对环境噪声具有更强的抗干扰能力。振荡频率随着Vctrl的增加而减小，随着bias即偏置电压的增大而增大。

然而，我们需要有补偿电路来生成控制VCO振荡频率的控制电压Vctrl，同时能够补偿电源电压，温度和工艺角变化对振荡频率的影响。

图3 补偿模块的等效电路图

环形振荡器的频率受到温度和工艺参数漂移的影响，这主要是源于MOS管的性能随温度和工艺参数的漂移而改变。例如：当温度和工艺参数变化时，载流子迁移率和阈值电压将会随之变化，从而影响了环形振荡器的频率。当温度和工艺变化时，载流子的迁移率以及阈值电压会随着温度的改变而改变，具体变化的函数关系可用以下公式来表示：

其中α表示负温度系数，即阈值电压的绝对值随温度升高而减小。

当温度升高时，载流子迁移率减小，阈值电压绝对值减小，综合起来频率会降低，相反，温度降低时频率升高。

工艺模拟仿真分为五种情况，分别为：

ff,ss,tt,fs,sf。

其中，前者表示NMOS管的工艺情况，后者PMOS管的工艺情况，将两者组合即为系统的工艺情况。工艺中的最快和最慢指的是在工艺制造过程中，由于栅氧化层的厚度与掺杂浓度的不均匀所导致的MOS管阈值电压的值和载流子迁移率的不确定性，f表示阈值电压的绝对值最小，s表示阈值电压的绝对值最大，t表示中等。

当从快工艺角过渡到慢工艺角时，频率降低。

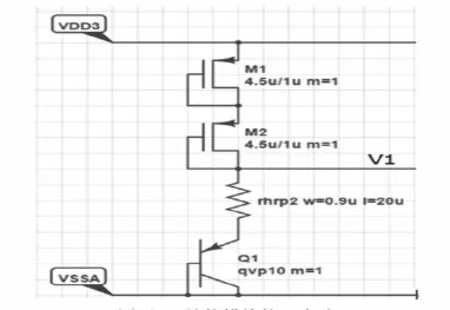
图4 补偿模块核心电路

补偿机理：

（1）温度补偿，由于三极管的VBE随着温度的升高而降低，所以V1具有负温度系数，也就补偿了温度对频率的影响；

（2）工艺补偿，在此次的华润上华工艺中，主要是PMOS的工艺角的变化对频率有较大影响。当从快工艺角到慢工艺角时，此支路上面的两个二极管连接的PMOS的阈值电压绝对值增大，所以等效电阻变大，导致V1（即M2管的漏极电压）减小，当从慢工艺角到快工艺角时，V1增大，从而可以补偿工艺角的变化对频率的影响；

（3）电源电压补偿：

Vctrl随着VDD呈直线上升，斜率近似为1，即（VDD -Vctrl）的值是一个定值，根据振荡频率f的表达式，Vctrl随VDD的变化有效的补偿了频率随VDD的变化。当然，VDD还通过影响工作电流，输出节点的电阻，对地电容来影响频率。

生成V1之后，再连接一个运算放大器，对补偿斜率进行调节，也就加大了补偿程度，以实现更加精确的补偿，由于电阻负反馈将V1增大到原来的2.25倍（即运放的输出V2=2.25*V1），此时输出太大，必须将其减去一个定值，即将运放的输出V2再接源一个跟随器(由M3和M4管组成)，减去一个Vgs的值，得到最终的Vctrl，来控制VCO的频率。

电路优点总结：

（1）带隙基准源输出的PTAT电流随电源电压，工艺角的变化非常小，与绝对温度成严格的正比例关系，为电路其他部分提供了稳定的偏置；

（2）VCO模块采用差分结构，相对于单端输入输出的延时单元来说,差分延时单元对环境噪声具有更强的抗干扰能力；

（3）整形模块达到了比较大的增益，将具有一定相位噪声的正弦波变成了数字方波；

（4）VCO模块中，Vctrl和偏置bias分开，这样就为我们补偿振荡频率随PVT的变化提供了两条途径，使得补偿的余地更大。（如果一个端口既作为偏置端口，又作为Vctrl,则频率稳定度肯定不如现在的效果好，因为一个端口同时“干了两件事情”。）

[1]原著Behzad Razavi,陈贵灿,程军,张瑞智,等译．模拟CMOS集成电路设计[M]．西安交通大学出版社．

[2] 李学军．带温度和工艺补偿的环形振荡器的设计,湖南大学,2012年7月．