考虑风险偏好的Stackelberg博弈模型及其在PPP项目中的数值求解

杜杨，丰景春.河海大学商学院，江苏南京200；2.金陵科技学院建筑工程学院，江苏南京269）



考虑风险偏好的Stackelberg博弈模型及其在PPP项目中的数值求解

杜杨1，2，丰景春1
1.河海大学商学院，江苏南京211100；
2.金陵科技学院建筑工程学院，江苏南京211169）

摘要：研究考虑风险偏好的Stackelberg博弈模型和均衡策略，针对公私合作制（PPP）项目补偿决策问题，根据前后补偿的特点，建立相应的补偿策略数学模型.分别进行集中决策和分散决策分析，得出PPP项目的最优补偿方案.通过数值分析比较和分析私人风险厌恶对于PPP补偿机制的影响.研究表明：私人投资者风险厌恶会导致政府方补偿成本增加，期望收益减少；私人投资者风险厌恶程度会影响补偿的配置方式，厌恶程度越低越倾向单一补偿，厌恶程度越高越倾向混合补偿.

关键词：Stackelberg博弈模型；风险偏好；公私合作制项目；政府补偿；决策分析

Stackelberg博弈模型的主要特点是针对主从决策问题，即从决策者地位不同，将博弈双方分成主动方和从属方.在公私合作制（public－private partnerships，PPP）项目中，两大主体政府与私人投资者明显地位不平等，而双方的决策过程为政府确定投资方案，私人投资者进行策略跟随，完全适合采用Stackelberg博弈模型进行分析.为了提高模型的实际适用性，博弈主体风险偏好等行为认知因素不能忽略.而现有PPP项目补偿研究中，要么将政府补偿当做实物期权［1－4］，要么专注于补偿调节、补偿政策等［5－10］，少数关注博弈互动研究又忽视了主体认知的影响［11］.因此，本文构建考虑风险偏好的Stackelberg博弈模型，并结合PPP项目情境设定参数进行求解分析.

1　基本博弈模型

考虑主体风险偏好差异的Stackelberg博弈模型为

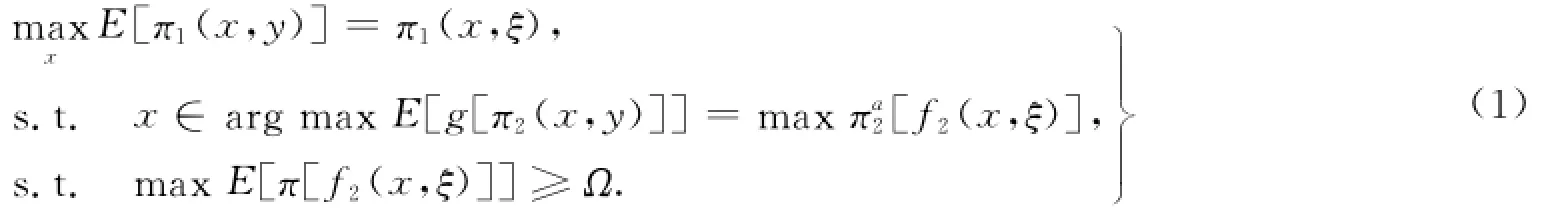
式（1）中：π［f1（.）］，π［f2（.）］分别为主动方和从属方的收益函数；Ω为从属方的保留效用；ξ为主动方对从属方的鼓励或惩罚条件；g［π2（x，ξ）］为从属方的效用函数；πa2［f1（x，ξ）］为效用函数g［π2（x，ξ）］的确定性等价收益.假定Arrow－Pratt绝对风险规避系数为ρ，则g［π2（x，ξ）］可表达为

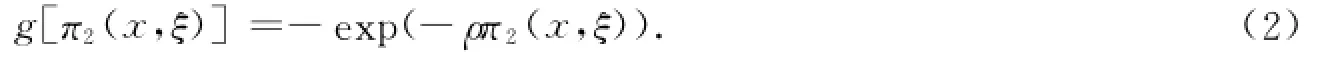
πa2（x，ξ）可以通过下式求出，即

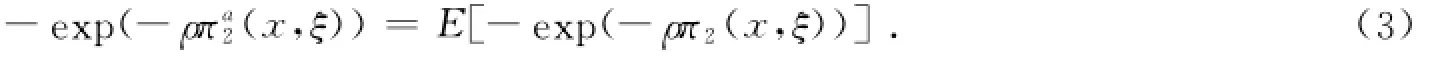
2　主要假设

假定项目需要的总投资为IP，其社会价值为V（IP），项目价值的系数为m，则V（IP）＝mIP，m＞0.PPP补偿主要包括前补偿（建设期）和后补偿（运营期）.假定公益性部分占项目总投资额比例为∮（0＜∮＜1），T为特许经营期，则单期前补偿为S＝∮IP.政府许诺给私人投资者R的基准运营收益，表达为Re＝nIP，n＞1.其中：n为基准运营收益率，可由资本资产定价模型（CAPM）进行测算.后补偿So由投资的实际收益与政府许诺的基准收益的差值决定，则单期后补偿为So＝θ（nIp－raIp）.其中：θ为运营期补偿系数；r为基于项目投资额的实际运营收益率，其为随机变量无法T∮a确定.假定ε为外界不确定因素决定的随机扰动量，ra为收益率的期望值，则Var（ε）＝σ2.

运营期维护成本为C（Ip），项目规模越大维护成本越大，且边际成本递增，则可设C（Ip）＝kIαP.其中：k，α为投资转换为维护成本的参数，且k＞0，α＞1.

3　PPP博弈模型构建

3.1 支付函数

根据以上假设，不考虑资金的时间价值，私人投资者P的单期支付函数为

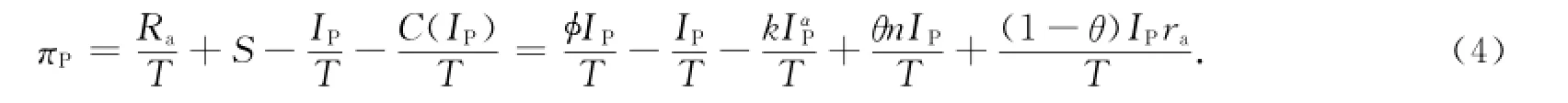
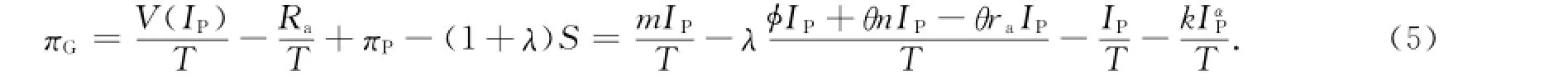
公共资金有影子价格［12］，设影子价格系数为（1＋λ）S，且λ＞0，则政府G的单期支函数为式（5）中：V（IP）－Ra为项目消费者剩余；π为生产者剩余；（1＋λ）S/T为政府支付的公共资金成本.TTP

3.2 Stackelberg博弈决策模型

政府方效用函数即为收益函数g（πG），而私人投资者需要考虑其风险偏好，其效用函数为p（πP）＝－exp（－ρπP）.（6）

式（6）中：ρ为绝对风险规避系数.易证，p′（πP）＞0，p″（πP）＜0.

由式（3），（6）和效用函数的递增性易证，私人投资者最大化期望效用等价于最大化等价收益πAP，即

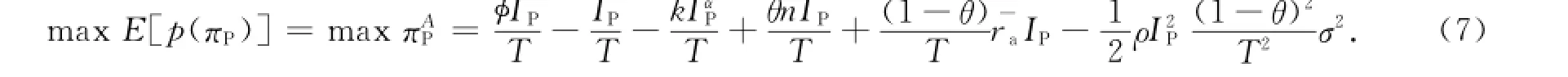
假定私人投资者的保留效用为ω，则其投资意愿需满足参与约束条件，即

政府为风险中性，其期望效用函数与期望收益等价，即

4　博弈决策分析

4.1 集中决策博弈分析

集中决策是指在PPP项目中政府完全掌握主导权，占有更多信息，能够代替私人投资者确定项目投资额以及补偿方案，并达成社会效益最大化.

根据式（8），（9），并令

则集中补偿决策模型可表达为

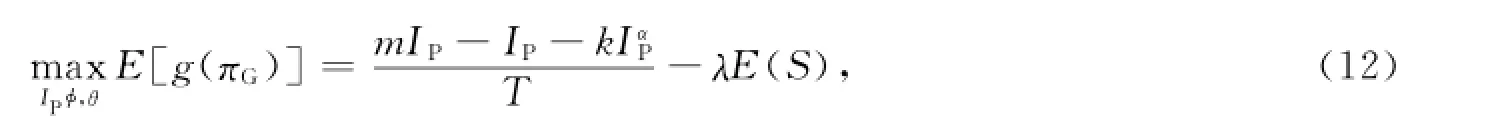
结合式（10），（11），（13），有

式（14）代入式（12），可得

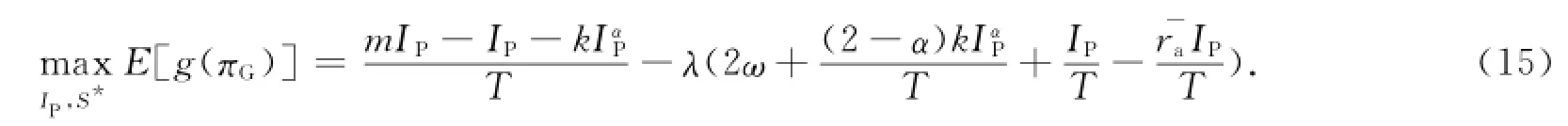
当式（15）一阶条件等于0时，有最优投资规模策略I＊P，可得

最优单期补偿为

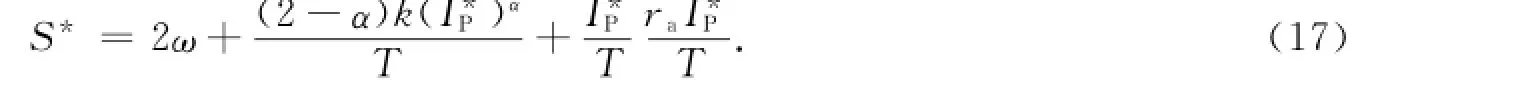
其中，单期运营期望补偿和单期建设期补偿分别为

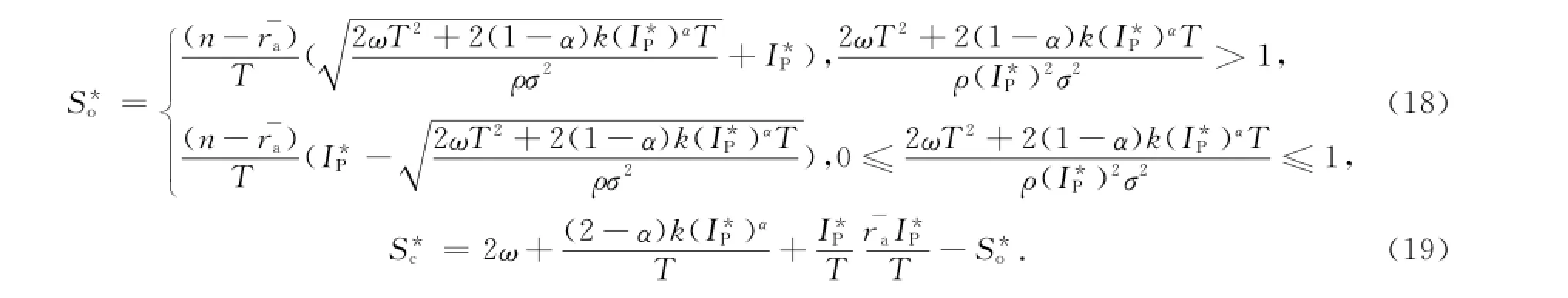
命题1 在集中决策时，项目存在最优投资规模I＊P如式（16），并有最优补偿方案如式（17）.其中：最优运营期补偿如式（18）；最优建设期补偿如式（19）.

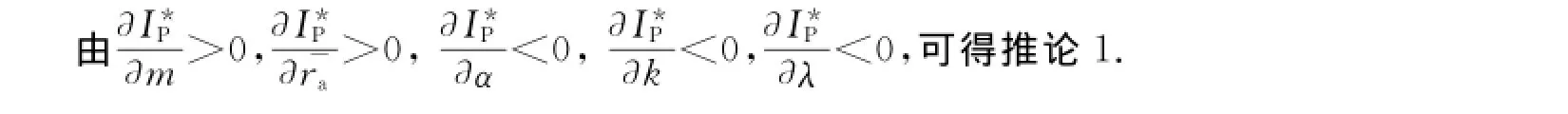
推论1 在集中决策模式下，PPP项目的最优投资规模与项目的社会价值、运营收益期望值呈正相关，与公共资金成本、项目维护成本呈负相关.PPP项目的最优期望补偿大小与建设期投资、维护成本、私人风险成本以及私人投资者风险厌恶程度呈正相关关系，与期望运营收益呈负相关.

由式（17）可知：当S＊≠0时，综上分析，可得推论2.

推论2 在集中决策模式下，当PPP模式适用，即单期补偿S＊不为0的前提下，单期补偿S＊与期望运营收益、特许运营期呈负相关，与私人投资者保留效用、维护成本、建设投资呈正相关.4.2 分散决策博弈分析

由于政府并不掌握私人投资者的全部信息，要想达到双方利益协调，还必须从分散决策的角度做博弈分析.可以采用逆向归纳法求解，首先考虑私人投资者的策略选择，其一阶条件和二阶条件为

分散决策第一阶段下，私人投资者的最优策略IP＊＊由下式给出

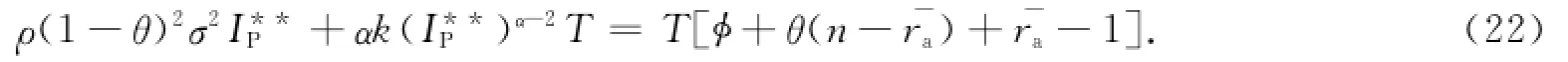
命题2 私人投资者存在最优投资策略IP＊＊满足式（22），且私人投资者的投资水平与建设期补偿系数，项目特许运营期、运营期补偿系数、基准运营收益率、运营期实际收益率期望值、运营风险和私人投资者风险态度等影响因素有关.各影响因素之间的相关性，如表1所示.表1中：“0”表示不相关；“＋”表示正相关；“－”表示负相关.

表1　私人投资者最优策略各影响因素的相关性Tab.1　Correlation of influencing factors of private investor optimal strategy

4.3 政府博弈分析

分散决策的第二阶段，政府掌握博弈主导权预测到私人投资的最优投资策略I＊＊P，则政府的优化问题转变为

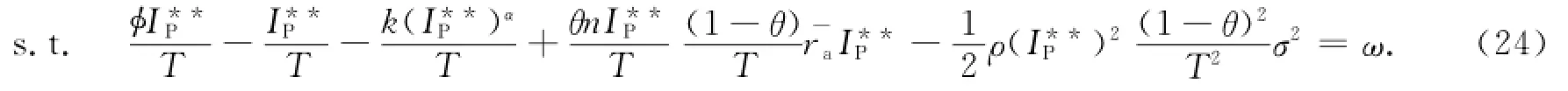
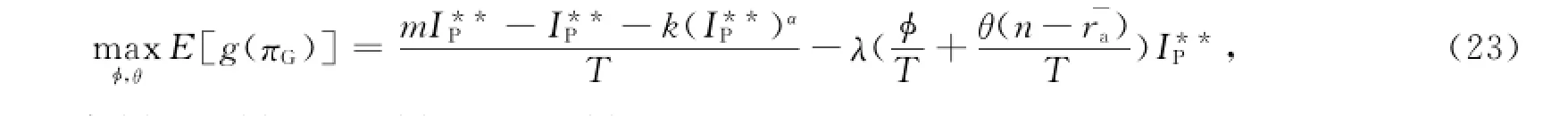
将式24代回式23可得

令式（25）的一阶条件等于0，可得

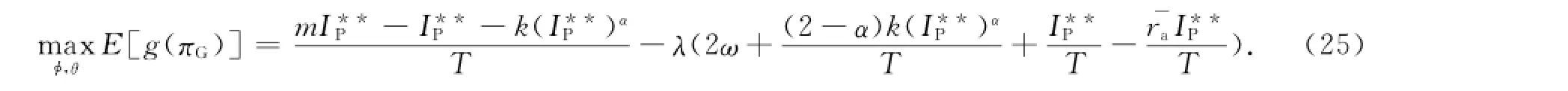
式（26）中：上标＊＊＊表示政府在分散决策第二阶段的最优策略.易知，I＊＊＊P满足式（22），即I＊＊＊P＝I＊＊P.分散决策下政府方最优补偿设计为

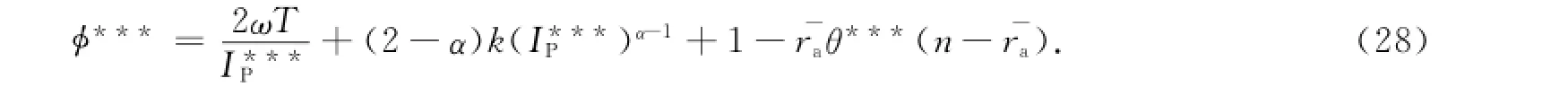
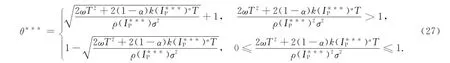
归纳上述分析可得命题3和推论3.

命题3 在分散决策下，私人投资者的最优投资策略为IP＊＊满足式（22），政府方通过提供参数为（θ＊＊，φ＊＊）的补偿方案，可诱导出项目的最优投资规模IP＊＊＊如式（26），θ＊＊，φ＊＊＊可分别由式（27），（28）给出.

推论3 补贴方案（θ＊＊＊，φ＊＊＊）可以使PPP项目私人投资者和政府的利益达到协调，在满足私人投资者最优策略的条件下，达到项目的最优投资规模.此时，私人投资者的效用达到其自身的保留效用，（θ＊＊＊，φ＊＊＊）补贴方案下的社会最大净效益也达到最大，形成有效补偿机制.

5　数值分析

5.1 风险偏好对激励效能和补偿方式的影响

项目各参数赋值如下：m＝2.7；λ＝0.5；k＝0.1；α＝1.1；ra＝1.01；ω＝1×108.

根据式（27），（28），使用Mathematica 9.0软件作数值分析结果，如图1，2所示.图1，2中：ρ为绝对风险规避系数；θ为运营期补偿系数.由图1（a）可知：当私人投资者风险厌恶程度较低时，可以选择采取完全后补偿（运营期补偿）方式（φ＝0）；但随着私人投资者厌恶程度加深，必须提高建设期补偿的比例.

当政府财政资金充足或项目预期收益不足时，只要私人投资者厌恶程度合适，政府有可能采取完全建设期补偿的方式诱导出最优投资规模.由图2可知：随着私人投资者厌恶程度的加深，前补偿降低而后补偿增加.

图1　θ＞1时，ρ对θ和∮的影响Fig.1　Whenθ＞1，influence ofρchanges onθandφ

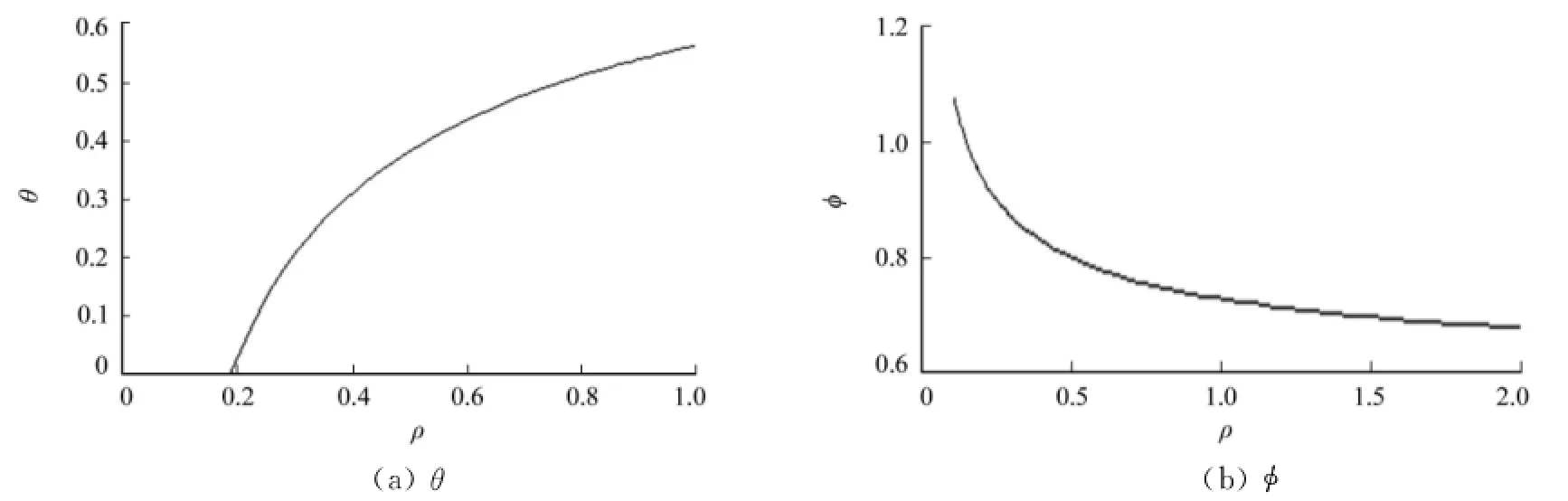
图2　0≤θ＜1时，ρ对θ和∮的影响Fig.2　When 0≤θ＜1，influence ofρchanges onθandφ

5.2 私方风险偏好政府效用的影响

由于私人投资者的效用始终为ω，因此，只讨论风险厌恶程度对政府收益的影响.沿用节5.1其他赋值，令ρ1＝0，ρ2＝1，可分别得到风险厌恶和风险中性政府期望效益曲线，如图3所示.图3中：πG为政府期望收益；i为投资规模.

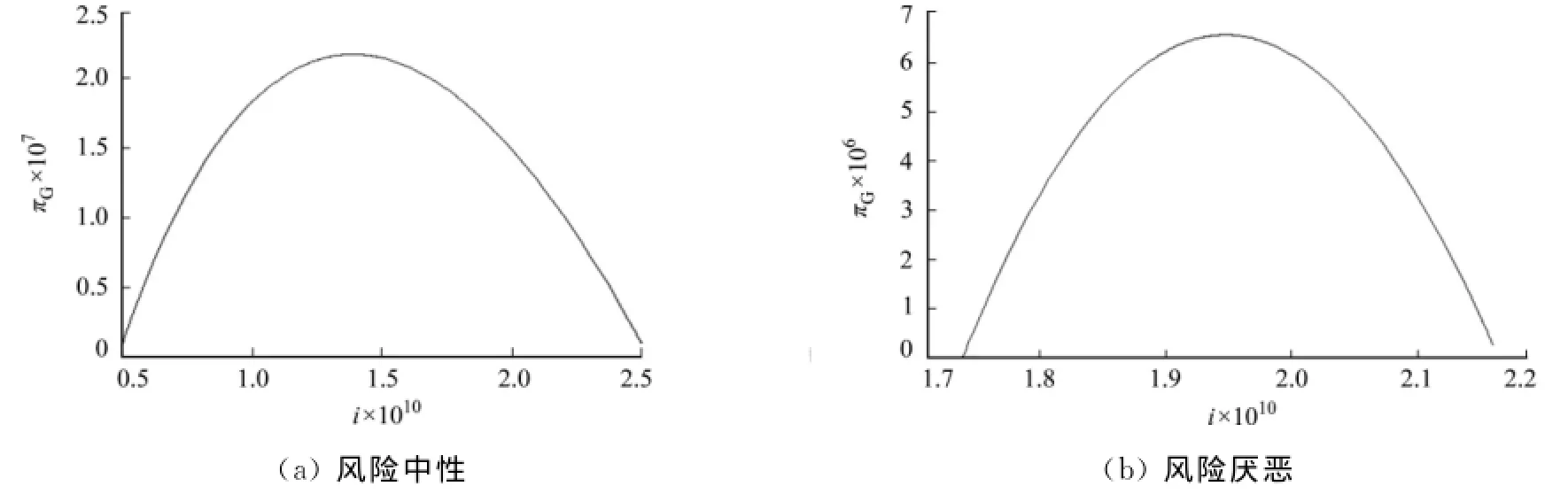
图3　私人投资者风险中性和风险厌恶假设下的政府收益曲线Fig.3　Curves of government utility in risk－neutral and risk－aversion respectively

由图3（a），（b）可知：在设定的参数下，考虑私方风险厌恶在最优投资规模处的政府期望收益要小于风险中性假设下的政府期望收益.当私人投资者保留效用很大或期望运营收益很小时，可能造成无论给出何种补偿方案都无法避免政府效用出现负值的情况，此时，PPP模式就不再适用.

6　结束语

在考虑公私双方风险偏好差异的基础上，针对PPP项目补偿问题，构建公私双方的Stackelberg博弈模型，探讨了协调公私利益的有效机制，并得出了补偿方案的最优形式，通过数值分析研究了私人风险厌恶对社会净效益和补偿方式的影响.结果表明：考虑私人风险厌恶会导致政府期望效用小于风险中性情形；私人投资者风险厌恶的变化会影响补偿的最优配置方式.当运营补偿优先（θ＞1）时，私人风险厌恶程度的增加会降低运营补偿的比例，提高建设期补偿的比例；相反，私人风险厌恶程度的增加会加大最优补偿方案中运营补偿的比例，减少建设期补偿的比例.

参考文献：

［1］MASON S P，BALDWIN C Y.Evaluation of government subsidies to large－scale energy projects：A contingent claims approach［J］.Advances in Futures and Options Research，1988，33（1）：169－181.

［2］HO S P，LIU L Y.An option pricing－based model for evaluating the financial viability of privatized infrastructure projects［J］.Construction Management and Economics，2002，20（2）：143－156.

［3］李明顺，陈涛，滕敏.交通基础设施PPP项目实物期权定价及敏感性分析［J］.系统工程，2011，29（3）：67－73.

［4］郭健.公路基础设施PPP项目交通量风险分担策略研究［J］.管理评论，2013，25（7）：11－19，37.

［5］CHEAH C，LIU Ji－cai.Valuing governmental support in infrastructure projects as real options using Monte Carlo simulation［J］.Construction Management and Economics，2006，24（5）：545－554.

［6］JUN J.Appraisal of combined agreements in BOT project finance：Focused on minimum revenue guarantee and revenue capagreements［J］.International Journal of Strategic Property Management，2010，14（2）：139－155.

［7］WIBOWO A.Valuing guarantees in a BOT infrastructure project［J］.Engineering，Construction and Architectural Management，2004，11（6）：395－403.

［8］FEARNLEY N，BEKKEN J T，NORHEIM B.Optimal performance－based subsidies in Norwegian intercity rail transport［J］.International Journal of Transport Management，2004，2（1）：29－38.

［9］邓小鹏，熊伟，袁竞峰，等.基于各方满意的PPP项目动态调价与补贴模型及实证研究［J］.东南大学学报：自然科学版，2009，39（6）：1252－1257.

［10］CHOWDHRURY A N，CHAROENNGAM C.Factors influencing finance on PPP projects in Asia：A legal framework to reach the goal［J］.International Journal of Project Management，2009，27（1）：51－58.

［11］吴孝灵，周晶，彭以忱，等.基于公私博弈的PPP项目政府补偿机制研究［J］.中国管理科学，2013，21（增刊1）：198－204.

［12］刘明.中国公共资金边际成本估量与分析［J］.财经论丛，2009（6）：31－38.

（责任编辑：黄晓楠 英文审校：黄心中）

Stackelberg Game Model with Risk Preference and Numerical Solving in the PPP Project Problem

DU Yang1，2，FENG Jing－chun1
（1.Business School，Hehai University，Nanjing 211100，China；
2.Architectural Engineering Institute，Jinling Institute of Technology，Nanjing 210098，China）

Abstract：Based on the game theory and risk preference，the Stackelberg game model and equilibrium strategy are established on decision－making problem for government compensation in public－private partnerships（PPP）project.After centralization and decentralization decision analysis，the optimal plan is obtained.Research results show that the compensation cost and the optimal scale of investment considering the risk preference are more than the risk－neutral hypothesis and the effects on the government′s expected revenue are contrary.The research results also show the degree of the private′s risk－aversion will affect the configuration mode of the government compensation.

Keywords：stackelberg game model；risk preference；public－private partnerships project；government compensation；decision analysis

通信作者：丰景春（1963－），男，教授，博士，主要从事工程管理和项目管理及其信息化方面的研究.E－mail：feng.jingchun＠163.com.

中图分类号：C 931；O 29

文献标志码：A

文章编号：1000－5013（2015）04－0472－06

doi：10.11830/ISSN.1000－5013.2015.04.0472

收稿日期：2015－06－16

基金项目：国家社科基金重点资助项目（14AZD024）；中央高校基本科研业务费专项资金资助项目（2014B09014）；中国博士后科学基金资助项目（2014M551498）