基于地理加权回归的区域森林碳储量估计
2015-12-29郭含茹张茂震徐丽华袁振花陈田阁
郭含茹,张茂震,徐丽华,袁振花,陈田阁
(1.浙江农林大学 浙江省森林生态系统碳循环与固碳减排重点实验室,浙江 临安 311300;2.浙江农林大学 环境与资源学院,浙江 临安311300;3.河南省濮阳市华龙区科学技术局,河南濮阳457001)
基于地理加权回归的区域森林碳储量估计
郭含茹1,2,张茂震1,2,徐丽华1,2,袁振花1,2,陈田阁3
(1.浙江农林大学 浙江省森林生态系统碳循环与固碳减排重点实验室,浙江 临安 311300;2.浙江农林大学 环境与资源学院,浙江 临安311300;3.河南省濮阳市华龙区科学技术局,河南濮阳457001)
森林碳储量与其调查因子之间的关系及其空间相关性特征是区域森林碳储量及其分布估计模型建立的基础,然而某一调查因子在不同空间位置对森林碳储量估计的影响程度存在差异。地理加权回归方法考虑了调查因子作用的空间异质性,进行局部回归估计。以浙江省台州市仙居县森林资源二类调查样地实测数据为数据源,利用地理加权回归方法结合陆地探测卫星系统Landsat TM影像数据进行森林碳储量及其密度的分布估计,并检验地理和海拔加权回归在地势平缓的区域是否可用。结果表明:①仙居县森林地上部分总碳储量3.132×106Mg,与样地实测统计得到的全县碳储量3.192×106Mg相差1.880%;地理加权回归模型估计结果与实际碳密度分布情况相一致,研究区内碳密度的取值范围为0~89.964 Mg·hm-2,保留了70%以上的空间异质性特征;基于地理加权回归的森林地上部分碳储量估计方法是有效的,地理加权回归在区域碳储量方面估计结果合理且精度较高。②在地势较为平缓的地区,海拔对植被的影响不显著,地理和海拔加权回归并不适用;若将海拔作为解释变量加入建模,能够提高估计精度,但存在多重共线性问题。图6表9参26
森林生态学;森林碳储量;空间异质性;地理加权回归;地理和海拔加权回归
森林是陆地生态系统中最大的碳库,在全球碳循环过程中占据重要地位。Phillips等[1]对热带森林生物量的研究表明:热带森林生物量的较小波动即可引起全球碳循环的显著变化。可见,森林生态系统碳储量和动态的研究直接关系到降低大气中二氧化碳浓度、减缓全球气候变暖的重大议题。中国作为一个发展中国家,能源的消耗和二氧化碳的排放量相对较大,且中国在全球固碳减排行动中充当着重要的角色。精准地估算中国森林植被碳储量,是进行碳收支和碳交易评估的前提[2]。区域森林碳储量的估测普遍采用的方法是由直接或间接测定森林植被的生产量与生物现存量再乘以生物量中碳元素的含量,推算得到[3]。森林植被的含碳率一般为0.45~0.50[4]。本研究采用政府间气候变化专门委员会(IPCC)提供的默认参数0.50计[5]。目前,国内外应用最为广泛的生物量估测方法有3种:样地清查法、涡度相关法、应用遥感等新技术的模型模拟法[6]。近年来,随着遥感、地理信息系统(GIS)等新技术在森林生物量估测方面的应用,第3种方法在森林生物量估算研究中应用最为广泛。基于GIS的地统计学分析为研究森林调查因子的空间相关性和依赖性现象提供了科学方法[7]。李明诗等[8]的研究表明:利用光谱、地形及纹理特征对森林生物量进行建模可以提高森林生物量的估测精度,且不同树种与不同的特征具有强相关性,特征贡献为0.044~0.205。常规基于普通最小二乘法(OLS)的生物量模型估测,忽略了调查因子作用的空间异质性。而实际上,某一调查因子在不同空间位置对生物量估测的影响程度是有差异的。在空间建模领域,一些统计技术已经发展到模拟空间变量之间的空间关系。在探索空间关系的异质性方面,最有力的工具之一就是地理加权回归(GWR)[9]。地理加权回归方法是传统回归分析方法的扩展,进行局部而非全局的参数估计,GWR方法在数据集的所有位置点的参数进行估计时考虑了非平稳性的关系,针对每一个坐标位置点都有相对应的参数。GWR方法被广泛地运用到各领域研究中,且均得到较好的研究结果。邵一希等[10]将地理加权回归方法应用在区域土地利用格局模拟建模中,与OLS的Logistic回归模型进行比较,得出GWR模型可以得到更加精确的拟合优度和拟合准确率。郭龙等[11]的研究表明:在土壤属性空间预测领域,GWR方法比协同克里格方法具有更高的预测精度。然而,林业遥感应用领域,GWR建模是一个相对未开发的区域[9]。Propastin[12]针对多山的热带雨林地区地上生物量的估测进行了地理加权模型的改进研究,考虑到海拔对森林生物量的分布影响,将高度影响作为第三维度加入到GWR加权矩阵来扩展GWR模型,得到地理和海拔加权回归(GAWR)模型。结果表明:针对海拔高度影响较大的数据集,GAWR模型比GWR模型效果更好[9]。但对于不同于多山的热带雨林的其他地形地貌植被类型等来说,在地上生物量的估测研究中,尚未有明确的结论证明地理加权回归方法是否也可以获得较高的估测精度;如果应用数据来自于不太明显的海拔梯度的区域,第三维度的加入是否会有更好的效果?或者使用不同模型与GWR模型的比较研究,也是值得深入研究的。本研究以浙江省台州市仙居县为研究区,尝试地理加权回归方法估计区域森林碳储量,利用实测地上部分碳储量数据和美国陆地探测卫星系统专题绘图仪(Landsat TM)数据建立局部回归模型,并检验在海拔较为平缓的地区,地理和海拔加权回归模型是否可用,以期提高森林碳储量的估计精度,对进一步量化区域森林碳汇能力具有重要现实意义。
1 材料和数据
1.1 研究区概况
仙居县位于台州市西部(28°28′~28°59′N,120°17′~120°55′E)(图1),总面积为20.131 8×104hm2。全县地形从外向内倾斜,略向东倾,其间有大小不等、错落相间的谷地和盆地。属于亚热带季风气候,雨水充沛。仙居县是浙江省重点林区县之一,2011年全县森林覆盖率为77.9%,最高海拔1 384.4 m。研究区中部狭长地带为平缓地带和城镇聚居区,西南部是国家级森林公园。研究区内杉木Cunninghamia lanceolata,马尾松Pinus massonania和阔叶树占主要地位。
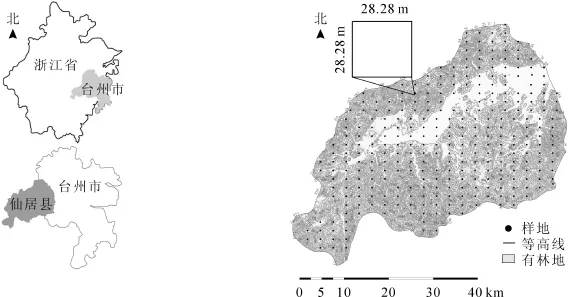
图1 研究区位置和样地分布示意图Figure 1 Location of the study area and the plots distribution
1.2 数据准备
1.2.1 地面调查数据 研究所使用的森林资源数据来源于仙居县2008年森林资源二类清查中的抽样调查数据。按等距抽样方法进行抽样调查,抽样总体为仙居县行政区范围。样地间距2.0 km×3.0 km,共有样地307个,均为28.28 m×28.28 m的正方形,面积0.08 hm2(图1)。野外样地测设由全球定位系统(GPS)定位,水平位置误差±(5~8)m。样地调查内容包括树种、平均年龄、平均胸径、平均树高、地类、地貌、海拔、坡向、坡位、坡度等。样木起测胸径为5 cm。调查样木分为杉木、马尾松、硬阔、软阔等4个树种(组)。根据利用浙江省2009年森林资源连续清查体系(简称CFI体系)样地数据建立的单株立木生物量模型计算地上部分生物量(表1)[13-15];求和得到各样地总的地上部分生物量,并根据生物量/碳储量转换系数和样地面积将地上部分生物量换算成碳密度(Mg·hm-2);其中生物量/碳储量转换系数选用采用政府间气候变化专门委员会(IPCC)提供的默认参数0.50计[5]。通过每木检尺数据计算出每个样地的地上部分生物量,其碳密度值为0~87.005 Mg·hm-2,平均值为15.854 Mg·hm-2,标准差为16.747 Mg·hm-2,变异系数达到1.056,属于强变异类型。中位数为10.208 Mg·hm-2,呈现出明显的负偏(表2)。对碳密度及相关地形因子进行描述性统计的结果如表2,其相关性分析如表3。这几种统计量均存在一定的空间变异性,其中碳密度、坡度属于强变异类型,其他均属于中等变异类型。在0.01显著水平下,森林碳密度与坡位、海拔等的相关系数为-0.337~0.294。

表1 研究区碳密度计算Table 1 Carbon density calculated in the study area

表2 样本碳密度统计特征Table 2 Statistical description of the plot carbon density

表3 地形因子与碳密度的相关性分析Table 3 Correlation between carbon density and the inventory factors
1.2.2 遥感数据 研究使用2007年10月仙居县全境Landsat TM影像数据,空间分辨率为30 m×30 m,与样地大小基本吻合。图像的预处理包括常见的卫星数据处理步骤,如几何校正和辐射校正等处理,总误差小于1个像元。利用软件Erdas 9.2提取307个样地所对应的遥感图像6个波段灰度值,即band1,band2,band3,band4,band5和band7。通过波段/波段组合与碳密度相关性分析选择建模变量。如表4,其中Band3与碳密度呈负相关,在0.01显著水平下达到-0.436,为最高;植被指数NDVI,SAVI与碳密度的相关性在0.01显著性水平下达到0.35以上,呈正相关。

表4 遥感波段及其组合与碳密度相关性分析Table 4 Correlation between carbon density and the band combination of the remote sensed data
1.2.3 变量筛选 通过相关分析发现,坡位,Landsat TM band1,band2,band3,band7,NDVI,SAVI与森林碳密度均在0.01显著水平下显著相关。考虑到其中band3是叶绿素的主要吸收波段,NDVI在森林碳估测中被普遍使用,SAVI为土壤调整植被指数,所以将坡位,band3,NDVI,SAVI作为建模的备选因子。由于参与模拟建模的解释变量不仅要与因变量显著相关,而且解释变量间要求相互独立,所以对以上4个备选因子和碳密度进行相关分析(表5)。结果表明:解释变量之间同样具有显著相关性,甚至更高,不适合联合建模,若联合建模解释变量之间存在共线性,最终确定选用band3与碳密度进行独立建模。为了与地理和海拔加权回归模型进行对比,分别尝试band3独立建模、band3和海拔联合建模、地理和海拔加权回归建模。

表5 解释变量与因变量的相关性分析Table 5 Correlation between the explanatory variables and the dependent variable
2 研究方法
2.1 地理加权回归
地理加权回归(GWR)方法是传统回归方法的扩展,可以进行局部参数估计。其本质思想是为数据集中各要素建立独立的方程[18]。研究区内任何位置的参数估计,由1个因变量和1个或多个自变量结合已知样本信息的空间关系构成的空间权重实现。根据地理学第一定律,相互接近的观测点数据贡献更多的影响,GWR模型以一个关于距离的函数进行加权,函数的回归系数是观测点地理位置的位置函数。全局空间回归假定回归参数在整个研究区域内是一致的,GWR模型的参数不再保持不变,而是随着地理位置的变化而变化。研究区内抽样得到若干观测点,可视为将整个研究区分为这若干区域,针对各观测点分别建立模型,作为该观测点所在区域的局部回归方程来进行区域化变量的估计。GWR的模型结构可表达为:
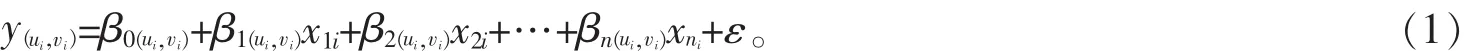
式(1)中:(ui,vi)表示点处的坐标,表示i点处的因变量,本研究中为i点处碳密度值;n表示变量的数目,则x1i~xni表示第n个变量在i点的值;β0表示截距,β0~βn表示第n个变量的估计回归系数。ε是误差项。对于传统全局回归模型,通过矩阵方程对参数进行估计:



式(4)中:wij表示附近点j相对于位置i的空间权重。在空间权重函数的选择上,最常被作为距离的连续函数来计算各点权重的是Gaussian函数:

然而由LeSage编写的GWR程序中的Gaussian函数表达式为:

另外,LeSage编写的GWR程序中还提供了一种Tricube权重函数:

本研究将分别尝试这3种权重函数。3个函数中,dij表示附近点j相对于位置i的距离,距离通常被定义为欧氏距离:

式(5~7)3个函数式中b是一个非负参数,表示带宽,是GWR模型中最重要的参数,模型参数的估计和模型预测的准确度很大程度上取决于带宽的选择,因为参数的估计只与带宽范围内的样本数据有关,带宽范围决定。带宽通常有2种表现方式:一种是最佳固定距离,另一种是最佳相邻点数。就Gaussian函数而言,不同的权重函数表达式又呈现出不同的带宽表示形式,式(5)中带宽b为某一固定距离,式(6)中带宽b与距离标准差的乘积代表某固定距离,所以,式(6)中的带宽b应是一个数值。下文将详细对带宽选择的结果进行展示;Tricube函数带宽则以邻近点个数表示,式(7)中d(b)表示带宽为b时,即包含b个邻近点,沿横坐标方向到点i最远的距离。带宽的选择通过Cleveland[19]和Bowman[20]提出的交叉验证(CV)方法[21-22]实现:

式(9)中:y^≠i(b)表示带宽为b时yi的模型预测值,其中≠i表示在对yi进行模拟的过程中,把yi视为未知,用带宽b范围内不包括样本i的其他已知样本信息对yi模拟建模。最终找到一个最优的带宽b值,使得函数CV(b)降到最低。根据Fotheringham等[20]提出的方法作为准则:Akaike信息准则(AAICc)值最小时,带宽b为最佳带宽。
2.2 地理和海拔加权回归
地理和海拔加权回归(GAWR)与地理加权回归(GWR)仅存在一点区别:如何定义空间关系。GWR模型通过二维地理空间坐标u,v来定义,而GAWR则通过三维地理空间坐标来定义[9]:

式(10)中:z代表点i处的海拔,作为第三维度参与计算空间距离。但多数情况下,海拔的差异性远远没有横纵坐标的差异性明显。就本研究来说,2个采样点间横坐标最小间距为3.0 km,纵坐标最小间距为2.0 km,而整个研究区的海拔差异最大只有1.0 km左右,此时式(10)中海拔只提供极小的贡献。为了改善这种情况,将海拔乘以一个扩大系数α以强调垂直方向上的影响因素:

最优扩大系数的选择与带宽的选择类似,同样采用交叉验证的方法,即变异系数(CV)值最小时,α的取值为最优。在本研究中扩大系数选用α=5。
2.3 回归参数的非平稳性测试
地理加权回归模型是局部回归模型,不同地理位置上模型的参数是变化的,于是需要判断参数是否在整个研究区内有显著变化,即参数的非平稳性测试。本研究采用Fotheringham等[23]提出的方法,将GWR模型的局部参数与普通最小二乘法回归的全局固定参数作对比,若局部估计的参数4分位值波动大于全局估计参数的一倍标准差范围,则认为模型的参数是显著非平稳的。
2.4 模型性能指标
为了检验GWR模型估计地上部分生物量的精度,本研究通过决定系数(R2),残差平方和(RRSS),均方根误差(RRMSE)等标准对不同试验结果进行统计描述。每一预测点的估计值与实际值的差的平方之和,即残差平方和,用来度量回归方程和数据组之间的总误差,此测量值越小,模型拟合度越高。均方根误差为估计值与实测值之差的平方的算术平均值再开方,也称为标准偏差。它反映了估计值偏离实测值的程度,在0.01或0.05显著性水平下,标准偏差越小,表示估计精度越高。式(13)和式(14)中,y^i,yi分别是因变量的估计值和实测值;总体平方和(RTSS)由回归平方和、残差平方和构成。

3 结果与分析
3.1 模型拟合
本研究借助GWR 4.0和Matlab软件平台,采用Gaussian和Tricube权重函数,对307个样地碳密度进行评估,以估计值相对于实测值的RRSS和RRMAE,来检验GWR模型的估计精度。软件GWR 4.0的估计结果为GWR(G)′和GWRa(G)′;由Matlab实现的GWR程序估计结果为GWR(G),GWR(T),GWRa(G),GWRa(T),GAWR(G)和GAWR(T),其中下标(G)表示Gaussian权函数,下标(T)表示Tricube权函数,下标a表示海拔作为解释变量之一的双变量GWR模型。
GWR模型参数的估计和模型预测的准确度很大程度上取决于带宽的选择,因为参数的估计只与带宽范围内的样本数据有关,所以需对带宽进行优化选择(图2)。GWR(G)的带宽默认为最小0.1,最大20.0,通过非线性优化进行交叉验证计算得分确定最优带宽(图2A)。GWR(G)′的带宽为某一固定距离,根据Akaike信息准则(AAICc),交叉验证(CV)准则确定最佳固定距离(图2B),随着带宽的增大,AAICc值和CV值有大幅度的减小,在带宽为2 000 m左右时,AAICc值和CV值的变化趋势趋于平缓,变化幅度减小。对于模型GWR(T),带宽为待测位置邻近点的个数q,程序默认邻近点个数最少应为变量数加2,即CVmin= nvar+2;qmax缺省设置为4倍的变量数,可根据实际情况改变。

图2 GWR模型的最优带宽确定Figure 2 Selection of the optimal bandwidth for the GWR model
各模型的结果均在表6中有所呈现。结果表明:研究区内碳密度可以通过地理加权回归建模得出;单一波段能够反映森林地上部分碳储量,适当增加解释变量的个数可以得到更好的估计结果,GWRa(G)′和GWRa(T)模型给出最小的残差平方和、均方根误差以及最高的R2,但由于存在多重共线性问题,海拔系数的t检验结果不显著;其次,GWR(G)′模型、GWR(T)模型给出较好的估计结果,决定系数可达到0.65以上,且估计结果在0.01显著水平下显著。
对于所有GWR模型和GAWR模型而言,选用的权重函数不同,带宽的表述形式也不同,建模的结果也不尽相同。GWR(G)′模型的估计结果与GWR(T)的估计结果较为相近。基于Tricube权重函数的模型总能模拟出最大的碳密度范围,GWR(T)估计结果的变异系数达到0.779,相较实测碳密度保留了原数据70%以上的变异特征。值得注意的是:GWR(G)模型估计结果与另外2个估计结果相差甚远。GWRa(G)模型比相对应的单变量模型估计精度不增反减,加入海拔作为解释变量之后,模型的估计精度降低了2.2%。另外2种模型精度略有提升,GWRa(T)模型比相对应的单变量模型提升了14.0%,GWRa(G)′模型提升9.0%。
将海拔信息加入到待测点的空间权重计算中,可以避免多元回归建模中的多重共线性;并且针对海拔因素贡献较小的问题,可通过加入一个扩大系数进行改善,即GWRS(G)和GAWRS(T)模型。然而针对本研究区,扩大系数的加入并没有起到明显的作用,对于GAWR(T)模型来说也只有微弱的改善,扩大系数的贡献仅有0.046。再对比GAWR与GWR的建模,结果表明:空间权重计算中海拔信息的加入,一定程度上降低了GWR回归模型的预测精度。GAWR5(T)模型比GWR(G)模型降低了0.6%;GAWR5(T)模型比GWR(T)模型降低10.4%,比GWRa(T)模型降低24.4%。对于本研究区来说海拔影响不明显,GAWR模型不适用。

表6 GWR模型、GAWR模型森林碳密度估计统计Table 6 Descriptive statistics of the predictive forest carbon density models by GWR and GAWR
3.2 回归系数的非平稳性
GWR模型参数波动范围的剧烈程度是评判模型参数在整个研究区内是否有显著变化的标准。若模型参数非平稳性显著,则表明该模型能反映更多的空间变异信息。如图3,以 GWR(G)和GWR(T)模型的参数范围为例,GWR(G)模型截距和自变量系数曲线是平稳的,2个参数的变化范围分别为16.430~35.320和-0.195~0.026;说明此GWR模型的系数局部差异不明显,几乎与全局回归模型无异。这也就解释了GWR(G)模型在估计研究区森林碳密度时精度较低的原因。
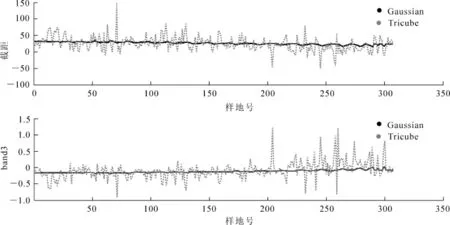
图3 GWR(G)和GWR(T)回归参数曲线Figure 3 Local regression parameter curve for GWR(G)and GER(T)
相对来说GWR(T)模型参数变化幅度明显优于GWR(G)模型(图3)。由表7可知:该模型截距的取值范围为-50.595~147.780,而不是全局回归模型中的恒定值26.718;band3的系数取值范围是-0.912~1.224,全局回归模型中为恒定值-0.124。对比表7和表8得出结论:GWR(T)截距的第1四分位与第3四分位的间距27.177小于全局回归截距的1倍标准差间距54.169;band3系数的第1四分位与第3四分位的间距0.225小于全局回归Band3系数的1倍标准差间距0.514。所以针对本研究区,GWR(T)模型参数存在一定的空间非平稳特征,但不显著,相对于全局回归能反映更多的空间变异信息。

表7 GWR(T)回归参数描述Table 7 Descriptive statistics of the local regression parameters from GWR(T)

表8 全局回归参数描述Table 8 Descriptive statistics of the global regression parameters
3.3 仙居县全县总碳储量及其分布估计
按照样地数据统计,仙居全县森林地上部分碳储量为3.192×106Mg,平均碳密度为15.854 Mg·hm-2。以GWR(T)模型为例估计仙居县全县森林地上部分碳储量及其分布(图4),由于地上部分森林碳密度值≥0,而由GWR(T)模型估计结果中出现极少数负值现象,估计结果为负的样地主要集中于仙居县城镇聚居区(图1),实测碳密度接近0,于是将估计结果中负值替换为0。还原0值后研究区碳密度为0~89.964 Mg·hm-2,分布趋势与实际情况相符:全县碳密度整体偏低,低值区域以城镇聚居区为中心向周边扩散,高值区域出现在研究区东北、西北及西南部;碳密度平均值为 15.555 Mg·hm-2,标准差为11.332 Mg·hm-2。研究区内森林地上部分总碳储量估计值为3.132×106Mg。总碳储量估计结果低于样地数据统计结果1.880%,吻合度较高。
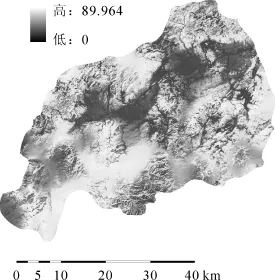
图4 碳密度分布估计图Figure 4 Carbon density estimation
以307个样地碳密度估计值与实测值的残差平方和(RRSS)和均方根误差(RRMSE),来检验地理加权回归模型的估计精度(图5,表9)。图5为样地碳储量实测值与相对应估计结果的对比,可以看出拟合程度好,估计结果与实际情况相一致,碳密度分布差异大,且大部分地区碳密度较低;碳密度估计值相对于实测值的RRSS为29 497.265 4 Mg·hm-2,RRMSE为9.802 Mg· hm-2。由图6估计偏差曲线可以看出:GWR模型单个点的残差波动范围较大,为-32.812~32.280 Mg· hm-2。对比图5和图6可以发现:当实测值较大时,更容易得到较大的估计误差,是由于在局部建模回归过程中,带宽范围内的样本数据对预测点的局部平滑作用,研究区内碳储量普遍偏低,个别具有较大碳密度的样地被低估。同理,具有较小碳密度的样地也在一定程度上被高估,但程度较低。
3.4 与其他方法的对比
为了验证地理加权回归方法在估计区域森林碳储量时的优势,我们用相同样本数据分别进行传统全局回归估计、协同克里格插值,将样地的预测结果对比分析见表9。传统的全局回归在反映遥感数据与生物量的关系中会丢失部分局部信息,通过全局统计导致较差的生物量估计。表9中全局回归、地理加权回归估计结果均值与实测碳密度值相一致,但变异系数差异明显,表明全局回归反映了研究区内区域化变量的平均状态;相对而言地理加权回归在保证平均水平的同时,更能反映空间数据变化规律的真实特征,保留了70%以上的空间异质性。在空间异质性分析方面,空间插值方法应用较广泛,主要依赖量化区域化变量的自相关性,通过相似的变异函数特征利用变程范围内的数据对未知位置进行预测。协同克里格插值结果虽保留了近70%的空间异质性特征,但从碳密度取值范围、标准差、误差分析等来看,预测精度较低。地理加权回归的预测结果误差小,取值范围跨度大,更适合与对森林碳储量空间变异性的分析和预测。地理加权回归模型具有较高的空间模拟预测精度。
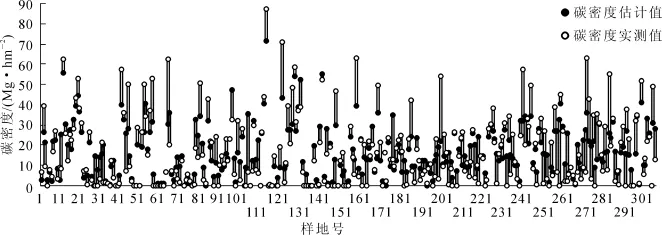
图5 样地碳密度估计值与实测值比较Figure 5 Carbon densities from GWR estimation and forest inventory

图6 样地碳密度估计偏差曲线Figure 6 Deviation curves of the forest carbon density estimate

表9 不同方法估计样地碳密度的对比Table 9 Comparison of carbon density estimation in the study area by different methods
4 结论与讨论
基于GWR(T)的2008年仙居县森林碳储量估计值为3.132×106Mg,平均碳密度为15.555 Mg·hm-2,比实测碳密度低1.880%,总量及其分布与实际一致;研究区内碳密度的取值范围为0~89.964 Mg·hm-2,保留了实测碳密度70%以上的空间异质性特征;决定系数0.65以上,且估计结果在0.01显著水平下显著。基于地理加权回归的森林地上部分碳储量估计方法是有效的,其估计结果精度高于传统回归和协同克里格插值方法。
本研究对地理与海拔加权回归模型(GAWR)在地势平缓地区的应用进行检测;作为与GAWR模型的对比,尝试了波段、海拔双变量的GWR模型建模。结果表明:GAWR模型的应用具有地域的特殊性,并不是针对所有地形地貌的区域GAWR模型都存在优势。这与海拔对植被的生长、分布的影响密切相关。在海拔对植被的影响不显著的平缓地区,GAWR并不适用;将海拔作为解释变量加入建模,能够提高碳储量估计精度,但存在多重共线性问题,使得双变量模型t检验不显著。
地理加权回归模型在估计区域森林碳储量时仍有一些值得注意和思考的问题:①在GWR估计中,带宽是影响估计结果精度的主要因素之一。尽管有Akaike信息准则和交叉验证准则在理论上指导寻找最优带宽,但实际操作中仍需结合具体情况综合考虑。空间权重计算方法的差异也会导致带宽的差异,GWR模型对带宽的变化非常敏感,所以针对不同研究区、研究数据选择合适的权重函数以确定最佳带宽是保证GWR模型精度的根本。②森林碳储量的大小与空间分布特征直接影响森林的碳汇潜力。目前,面临的一个挑战是,怎样从点测量尺度上推到更大的国家、区域和全球尺度上[24]。已有研究表明,地理加权回归分析对粒度变化呈现出一定的稳健性[25],因此,将其用于有明显地理差异的大尺度区域森林碳储量及其分布估计中,能取得更显著的效果。③目前。基于GWR模型的扩展模型还有:半参数地理加权回归(semiparametric GWR)模型,一部分自变量的参数为局部回归,另一部分自变量的参数为全局回归;地理加权泊松回归(GWPR)模型、地理加权Logistic回归(GWLR)模型等[26]。这些模型是否也适用于林业遥感领域,用以估计森林碳储量,是否能得到更好的估计精度,都值得进一步探索。
[1] PHILIPS O L,MALHI Y,HIGUCHI N,et al.Changes in the carbon balance of tropical forests:evidence from longterm plots[J].Science,1998,282(5388):439-442.
[2] 李海奎,雷渊才,曾伟生.基于森林清查资料的中国森林植被碳储量[J].林业科学,2011,47(7):7-12.
LI Haikui,LEI Yuancai,ZENG Weisheng.Forest carbon storage in china estimated using forestry inventory data[J]. Sci Silv Sin,2011,47(7):7-12.
[3] 王宏钰,沈欢.国内外森林碳储量估测研究现状[J].科技信息,2012(18):77.
WANG Hongyu,SHEN Huan.Estimation of forest carbon stocks both at home and abroad[J].Sci Technol Inf,2012(18):77.
[4] BROOK E J,SOWERS T,ORCHARDO J.Rapid variations in atmospheric methane concentration during the past 110 000 years[J].Science,1996,273(5278):1087-1091
[5] WATSON R T,NOBLE I R,BOLIN B,et al.Land Use,Land-Use Change and Forestry:Special Report of the IPCC[R].Cambridge:Cambridge University Press,2000:30-31.
[6] 曹吉鑫,田赟,王小平,等.森林碳汇的估算方法及其发展趋势[J].生态环境学报,2009,18(5):2001-2005.
CAO Jixin,TIAN Yun,WANG Xiaoping,et al.Estimation methods of forest sequestration and their prospects[J]. Ecol Environ Sci,2009,18(5):2001-2005.
[7] 李明阳,刘敏,刘米兰.基于GIS的森林调查因子地统计学分析 [J].南京林业大学学报:自然科学版,2010,34(6):66-70.
LI Mingyang,LIU Min,LIU Milan.GIS-based geostatistical analysis of forest inventory factors[J].J Nanjing For Univ Nat Sci Ed,2010,34(6):66-70.
[8] 李明诗,谭莹,潘洁,等.结合光谱、纹理及地形特征的森林生物量建模研究[J].遥感信息,2006(6):6-9.
LI Mingshi,TAN Ying,PAN Jie,et al.Modeling forest aboveground biomass by combining the spectrum,textures with topographic features[J].Rem Sens Inf,2006(6):6-9.
[9] PROPASTIN P.Modifying geographically weighted regression for estimating aboveground biomass in tropical rainforests by multispectral remote sensing data[J].Int J Appl Earth Observ Geoinform,2012,18:82-90.
[10] 邵一希,李满春,陈振杰,等.地理加权回归在区域土地利用格局模拟中的应用:以常州市孟河镇为例[J].地理科学,2010,30(1):92-97.
SHAO Yixi,LI Manchun,CHEN Zhenjie,et al.Simulation on regional spatial land use patterns using geographically weighted regression:a case study of Menghe Town,Changzhou[J].Sci Geogr Sin,2010,30(1):92-97.
[11] 郭龙,张海涛,陈家赢,等.基于协同克里格插值和地理加权回归模型的土壤属性空间预测比较[J].土壤学报,2012,49(5):1037-1042.
GUO Long,ZHANG Haitao,CHEN Jiaying,et al.Comparison between co-kriging model and geographocally weighted regression model in spatial arediction of soil attributes[J].Acta Pedol Sin,2012,49(5):1037-1042.
[12] PROPASTIN P.Modifying geographically weighted regression for estimating aboveground biomass in tropical rainforests by multispectral remote sensing data[J].Int J Appl Earth Observ Geoinf,2012,18(1):82-90.
[13] 朱汤军,沈楚楚,季碧勇,等.基于LULUCF温室气体清单编制的浙江省杉木林生物量换算因子[J].生态学报,2013,33(13):3925-3932.
ZHU Tangjun,SHEN Chuchu,JI Biyong,et al.Research on biomass expansion factor of Chinese fir forest in Zhejiang Province based on LULUCF greenhouse gas inventory[J].Acta Ecol Sin,2013,33(13):3925-3932.
[14] 沈楚楚,朱汤军,季碧勇,等.浙江省马尾松林生物量换算因子研究[J].浙江林业科技,2013,33(3):39-42.
SHEN Chuchu,ZHU Tangjun,JI Biyong,et al.Research on biomass expansion factor of Pinus massoniana forest in Zhejiang[J].J Zhejiang For Sci Technol,2013,33(3):39-42.
[15] 沈楚楚.浙江省主要树种(组)生物量转换因子研究[D].临安:浙江农林大学,2013.
SHEN Chuchu.The Research on Biomass Expansion Factors of the Dominant Tree Species in Zhejiang Province[D].Lin’an:Zhejiang A&F University,2013.
[16] WEISTER R L,ASRAR G,MILLER G P,et al.Assessing grassland biophysical characteristics from spectral measurements[J].Rem Sens Environ,1986,20(2):141-152.
[17] JOHN G L,DING Y,ROSS S L,et al.A change detection experiment using vegetation indices[J].Photogr Eng Rem Sens,1998,64(2):143-150.
[18] CHARLTON M,FOTHERINGHAM S.Geographically Weighted Regression:White Paper[M].Maynooth:National Centre for Geocomputation,National University of Ireland Maynooth,2009:5-11.
[19] CLEVELAND W S.Robust locally weighted regression and smoothing scatterplots[J].J Amer Stat Assoc,1979,74(368):829-836.
[20] BOWMAN A W.An alternative method of cross-validation for the smoothing of density estimates[J].Biometrika, 1984,71(2):353-360.
[21] SALVATI N,TZAVIDIS N,PRATESI M,et al.Small area estimation via M-quantile geographically weighted regression[J/OL].TEST,2012,21(1):1-28.
[22] 艾福利,庞西磊,汤庆园,等.基于地理加权回归模型的浙江省台风经济损失影响因子分布规律研究[J].北京师范大学学报:自然科学版,2013,49(1):61-67.
AI Fuli,PANG Xilei,TANG Qingyuan,et al.Impact factor distribution for economic losses due to Typhoon in Zhejiang province by geographical weighted regression[J].J Beijing Norm Univ Nat Sci,2013,49(1):61-67.
[23] FOTHERINGHAM A S,BRUNSDON C,CHARLTON M.Geographically Weighted Regression:The Analysis of Spatially Varying Relationship[M].West Sussex:Wiley,2002.
[24] WANG Guangxing,OYANA T,ZHANG Maozhen,et al.Mapping and spatial uncertainty analysis of forest vegetation carbon by combining national forest inventory data and satellite images[J].For Ecol Manage,2009,258(7):1275-1283.
[25] 覃文忠.地理加权回归基本理论与应用研究[D].上海:同济大学,2007.
TAN Wenzhong.The Basic Theoretics and Application Research on Geographically Weighted Regression[D]. Shanghai:Tongji University,2007.
[26] NAKAYA T.GWR4:Windows Application for Geographically Weighted Regression Modeling[R].Liverpool:GWR 4 Development Team,2012.
Geographically weighted regression based on estimation of regional forest carbon storage
GUO Hanru1,2,ZHANG Maozhen1,2,XU Lihua1,2,YUAN Zhenhua1,2,CHEN Tiange3
(1.Zhejiang Provincial Key Laboratory of Carbon Cycling in Forest Ecosystems and Carbon Sequestration, Zhejiang A&F University,Lin’an 311300,Zhejiang,China;2.School of Environmental&Resource Sciences, Zhejiang A&F University,Lin’an 311300,Zhejiang,China;3.Hualong District Science&Technology Bureau of Puyang City,Puyang 457001,Henan,China)
Global climate issues have confirmed the irreplaceable role forest carbon stocks play in the global carbon cycle.To research whether the geographically weighted regression(GWR)model method which considers the role of survey factors’spatial heterogeneity and establish the local regression model,can improve the estimation accuracy of forest carbon stocks,instead of the more commonly used methods of global regression model such as ordinary least squares analysis(OLS),we used forest management inventory data in Xianju County,Zhejiang Province,combined with Landsat TM image data developing local models using GWR to estimate forest carbon stock and its density.Available of geographically and altitudinal weighted regression(GAWR)model was then tested in smooth terrain.Analysis is included comparison to traditional regression and co-kriging interpolation.Results showed that the total forest aboveground carbon stocks estimated by the GWR(T)model for Xianju County were 3.132×106Mg,and carbon density ranged from 0 to 89.964 Mg·hm-2with a mean value of 15.555 Mg·hm-2.Meanwhile,the total forest aboveground carbon stocks calculated from diameter measurements were 3.192×106Mg with a mean value of 15.854 Mg·hm-2.The overall result from GWR(T)model was lower than diameter measured by 1.880%,R2=0.654(P<0.01),and carbon density distribution was consistent with the actual situation.The estimated results also had a higher accuracy with the RRMSE=9.802(P<0.01)than traditional regression method with the RRMSE=15.033(P<0.01)and co-kriging interpolation method with the RRMSE=16.427(P<0.01).GWR method can effectively estimate the regional forest aboveground carbon stocks reasonably and accurately,however,the GAWR model is not applicable for the areas with smooth terrain.Adding altitude as an explanatory variable in the modeling could improve estimation accuracy but would in turn create a multi-collinearity problem.[Ch,6 fig.9 tab.26 ref.]
forest ecology;forest carbon storage;spatial heterogeneity;geographically weighted regression(GWR);geographically and altitudinal weighted regression(GAWR)
S718.55,S757.2
A
2095-0756(2015)04-0497-12
10.11833/j.issn.2095-0756.2015.04.002
2014-09-19;
2014-11-01
国家自然科学基金资助项目(30972360,41201563);浙江省林业碳汇与计量创新团队资助项目(2012R10030-01)
郭含茹,从事森林碳汇计量和监测技术研究。E-mail:15869132363@163.com。通信作者:张茂震,教授,博士,从事森林碳汇计量和监测技术研究。E-mail:zhangmaozhen@163.com
