环境约束下长三角经济效率及全要素生产率增长—基于Luenberger指数的实证分析

■ 段海啸（1、河海大学商学院 2、河海大学产业经济研究所 南京210098

问题的提出

近年来，长三角地区社会经济高速发展，已经名副其实的成为强力推动我国经济发展的三大增长极之一（张慧文，2010）。2013年长三角地区生产总值（GRP）占全国GDP的23%，GRP增速12.2%，高于全国GDP平均增速。除此之外，长三角经济圈对我国内陆地区尤其是中部省份的区域经济也具有较强的带动作用和外溢效应（潘文卿，2008）。然而随着经济快速发展，长三角的环境问题也日益显现。长三角地区单位面积污染物排放强度已经达到了全国平均水平的5倍，挥之不去的雾霾以及水体污染问题已迫在眉睫。因此，如果不考虑环境承载力，仅将生产总值作为唯一指标考察长三角的发展绩效，则既缺乏全面性，也不符合我国近年来提倡的科学发展观。究竟长三角在考虑环境因素后的经济效率情况如何？经济增长的来源更多的是“量”的增加还是“质”的提升？本文试图从环境约束下的全要素生产率视角对以上问题进行探索。

目前，国内外学者将环境因素纳入分析框架对经济增长绩效进行研究的成果已较为丰富。国外研究主要围绕国家层面的环境全要素生产率测算比较展开。Kaneko et al（2004）对中国1987-2001年间基于省域数据的全要素生产率研究中发现，中国的环境管理出现恶化，全要素生产率增长中的环境产出下降了27%；Tzouvelekas et al（2007）基于面板数据研究了23个经合组织成员国（OECD）在环境约束下的全要素生产率增长，认为不考虑环境因素的传统估计方法会低估全要素生产率增长；国内研究按研究对象不同主要分为省级层面的比较研究和行业内的比较研究。如陈诗一（2009）、王兵（2010）、李玲（2011）和潘丹（2013）等分别以我国工业、火电行业、污染密集型产业以及农业为研究对象，测度了以上产业在环境约束下的全要素生产率以及技术进步和效率改善，并进行了省际比较，从中观经济层面将我国和谐社会构建中的产业发展、资源节约以及环境保护联系在一起。尽管如此，现有研究大部分仍过于宏观，从市域数据着手研究我国长三角环境全要素生产率的文献仍然凤毛麟角。因此，本文的研究目的即在考虑环境因素影响下从市域数据角度出发，测算长三角的环境效率和环境全要素生产率增长并进行分析，并对现有文献进行扩展。

研究方法

（一）环境技术的线性规划形式

..

本文首先根据Fare（2007）的方法构造包含长三角所有样本城市（DMU）的生产可能性集合。假设每一个DMU的投入向量为期望产出向量非期望产出向量在某一时点的投入产出值为(xn，ym，bp)。

为解决资源环境条件约束下的联合生产问题，环境技术在生产可能性集合满足闭集和有界集，投入和期望产出要素具有强可处置性，各种环境污染物作为非期望产出具有弱可处置性，以及期望和非期望产出符合零结合公理等假设条件下可模型化为如下的线性规划形式：

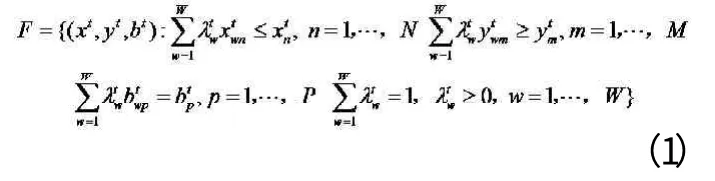
图1 长三角环境效率及分解

图2 2005-2012年长三角样本城市平均环境无效率及其分解

上式中λtw是每个投入产出要素的权重变量。约束条件表示此时所有样本城市构成的生产前沿面是处在规模报酬可变（VRS）下的前沿面。如无此限制，假设所有经济体都在最优规模下经营，则生产前沿面为在规模报酬不变（CRS）下的前沿面。

（二）方向性距离函数

资源环境约束下的全要素生产率增长要求在保证经济增长的同时尽可能实现能源消耗的降低和污染物排放的减少，传统的Shephard距离函数因为具有产出同比例增减的特性，从而不利于问题的研究。因此本文引入方向性距离函数，一则可以对环境效率做出评价，二则可以将其分解，找出导致环境无效的原因。根据Fukuyama&Weber（2009）和王兵（2010），本文定义资源和环境约束下的基于松弛向量的方向性距离函数（SBM）为：

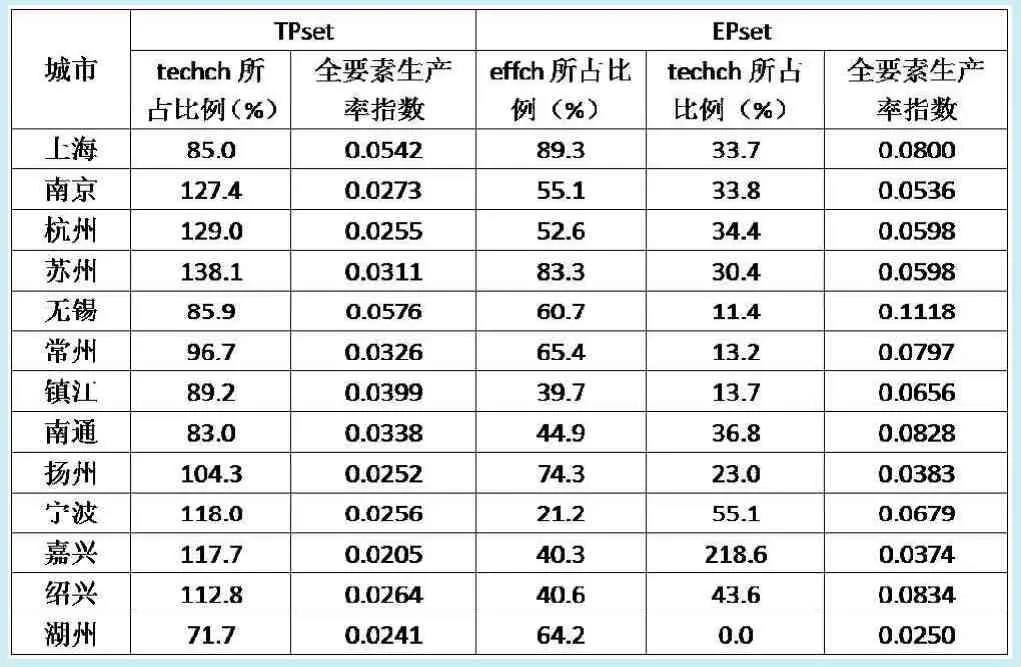
表1 样本城市环境全要素生产率指数及其分解

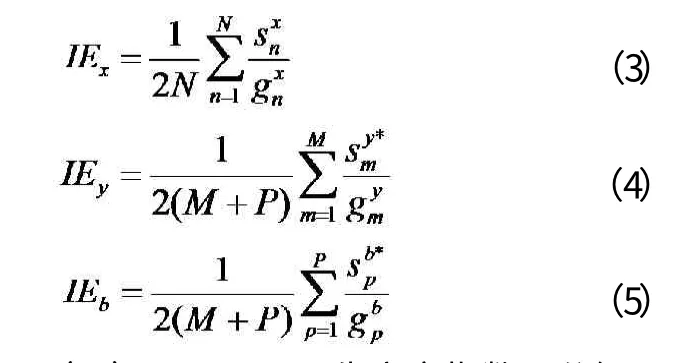
（三）Luenberger生产率指数及分解

本文采用差分形式的Luenberger指数对全要素生产率增长进行测度。1996年Chambers等在计算亚太经合组织（APEC）成员国生产率增长时定义了跨期的Luenberger生产率指数。本文根据Grosskopf（2003）的分解框架进行多项式分解后得到t期到t+1期的Luenberger生产率指数的公式为：

公式中①式为effch，表示纯效率变化；②式为techch，代表纯技术变化；③式为pech，表示规模效率变化；④式为sech，代表技术规模变化。通过对Luenberger生产率指数做如上分解，可以通过在八个条件下解方向性距离函数，得出环境全要素生产率增长及其来源。

样本和指标选取

本文分别选取江苏、浙江和上海三个省市的上海、南京、杭州、苏州、无锡、常州、镇江、南通、扬州、宁波、嘉兴、绍兴和湖州等城市为研究样本。具体指标选取如下：

劳动。作为投入要素之一的劳动应该用每个决策单元一定时期的全社会劳动工时来计算，但是《中国统计年鉴》并未将各省劳动工时数据给出，为研究带来一定困难。因此，本文用全社会从业人员数代替劳动工时作为劳动要素投入。

资本。测算全要素生产率所用的资本应该是各决策单元在一定时期资本总额的平均值。本文采用永续盘存法，运用估算资本存量时被广泛采用的公式（7）来估算各年资本存量：

上式中Kt-1代表t-1期决策单元的资本存量，δ代表每年存量资本的折旧率，It代表t年的全社会固定资本投资。可知，要得到Kt的值需要已知基年资本存量，折旧率δ以及每年固定资本投资额I。目前文献中对上述未知量的取值以及对资本存量的估算各不相同，测算出的资本存量K也差距较大。本文选择张军（2004）的方法来确定上述变量。即基期资本存量K等于当年投资额I除以10%，折旧率δ取9.16%。每年的投资总额经过固定资产投资指数调整变为可比价后带入公式计算，即可得到每年的资本存量。本文在测算城市生产率时所选择基期为2005年。

资源。本文将各种能源消耗折算成标准煤后的数量作为资源投入指标。

期望产出。本文选择决策单元当年的地区生产总值作为期望产出。地区生产总值为按基期的可比价格持续计算得到的相对数值。

非期望产出。要测算经济发展中的环境全要素生产率增长，环境污染物排放指标应能较好反映出在经济发展中各行各业排放入环境的污染物总和。但受制于数据的可获得性，本文将最能综合反映空气污染的二氧化硫（SO2）排放量和最能综合反映水体污染的化学需氧量（COD）排放量作为非期望产出指标纳入模型。

数据处理及实证分析

（一）环境效率及其分解

本文采取由全部样本城市的投入产出数据构建生产技术前沿面的方法。经过实证验算后发现，在“过去掌握的技术不被遗忘”假定条件下（Henderson，2001；林毅夫，2003），通过序列DEA的方法能够将不可行解降低至10%左右，并且出现不可行解的决策单元随着年份的不同而有所差异。因此，本文用序列DEA的方法对样本城市的投入产出数据进行处理（本文数据处理采用matlab2012软件）。

长三角地区环境效率。从2005年到2012年间，长三角环境非效率值逐年降低（见图1），说明长三角地区整体环境效率处于持续改善的过程中。从指标分解来看，长三角环境无效率的主要原因是其具有较高的SO2排放非效率值以及资本投入非效率值。如果按传统的变量同比变化来解释，长三角城市圈要达到环境有效需要减少5.4%的人员投入，6.6%的资本投入，5.8%的能源消耗以及8.3%的SO2排放和5%的COD排放。长三角在资本投入和COD排放方面的无效率值最高，揭示出区域内资本过度深化已成为环境无效率的重要因素。因此，淘汰落后产能，提高资本使用效率，控制污染物排放等措施的执行会在很大程度上提高长三角的环境效率。

在样本城市层面，环境效率最高的3个城市依次为常州、湖州和无锡，而环境效率最低的3个城市依次为南京、杭州和苏州（见图2）。环境效率高的城市均具有较低的污染排放非效率值和较低的单位能耗，而环境效率低的城市均呈现出高能耗和高排放的特点。能源的消耗和对环境的透支具有消费理论中的“棘轮效应”，即增长容易，下降困难，并且能源过量消耗和环境破坏会对经济的可持续发展留下较大隐患。正如近年来笼罩在我国长三角地区上空的雾霾，即是多年来粗放型经济发展方式所导致的恶果。目前花费在治理污染方面的投入可认为是以前年份为支撑经济快速增长而对环境的透支。但是本文的研究也显示出一个乐观的结果，即所有城市的污染物排放非效率和能源投入非效率值都呈现逐年下降趋势。

（二）全要素生产率指数及其分解

t期到t+1期的Luenberger指数的含义为从t期到t+1期全要素生产率的增长。本文分别在如下两种条件下构建生产可能性集合进行测算：

TPset为只投入资本K、劳动力L，产出生产总值Y的生产可能性集合，其计算出的全要素生产率指数，本文称为传统全要素生产率指数；EPset为投入资本K、劳动力L和资源E，产出生产总值Y、SO2和COD的生产可能性集合，其计算出的全要素生产率指数为加入资源环境约束下的全要素生产率指数，本文称为环境全要素生产率指数。

两种条件下所有样本城市全要素生产率均出现幅度不等的提高。传统全要素生产率的提升主要来自于技术进步，而在资源环境约束下则变为技术进步或效率进步混合驱动（见表1）。传统全要素生产率增长最快的3个城市依次为无锡、上海和镇江，无锡在2005年到2012年间，累积技术进步达到34.6%，上海为32.2%，镇江为28.9%。全要素生产率增长最慢的3个城市为扬州、嘉兴和杭州。三个城市的累积技术进步率分别为18.3%、16.9%和22%。可见，技术进步是推动全要素生产率增长的主要力量。

在加入环境因素进行分析后，从2005年到2012年环境全要素生产率增长率最高的3个城市为无锡、绍兴和南通。在EPset下大多数城市环境全要素生产率情况发生了变化，并且推动环境全要素生产率增长的主要因素也发生了改变，由单纯的技术进步推动变为技术进步和效率进步双重驱动。其中，上海、苏州、无锡等为效率改善推动型，嘉兴为技术进步推动型，其他城市环境全要素生产率增长则为技术进步和效率改善混合推动。

另外，所有样本城市在TPset下的全要素生产率指数均小于在EPset下测算出的值，这和王兵（2010）以及白雪洁（2009）得出的结论相同，即支持波特关于“环境管制促进生产率提升”的假说。但是从分解指标来看，却存在一些差异。在加入资源环境约束后，样本城市纯技术变化均出现下降而纯效率变化出现较大增加。纯效率进步和规模效率增加的一个可能解释是在约束条件增强后，即资源环境等管制增强时，企业成本增大，导致一些规模小，效率低的中小企业和小作坊退出市场，从而提升了纯效率和规模效率。在加入约束条件后纯技术变化出现降低的情况，可能是由于在环境管制与技术效率存在的“U”型关系中，本文所选样本目前仍处于U型曲线的下降阶段，即随着环境管制变严，技术效率降低。在达到最低点后，技术效率将会随着环境管制继续变严格而出现上升。

结论

本文在2005年到2012年长三角市域数据的基础上，分析了长三角地区环境效率以及环境全要素生产率增长情况。首先，从环境效率值看，长三角城市环境效率由高到低依次为常州、湖州和无锡。导致长三角环境无效的两个主要因素是SO2排放非效率以及资本投入非效率值偏高，说明长三角除面临SO2排放过多的问题外，还出现了较为突出的资本投入无效率，应注意控制资本的过度深化，提高资本的利用效率。另外，从2005年到2012年间，长三角各样本城市单位生产总值能耗以及单位生产总值污染物排放均实现了较大幅度的下降，这与国家近年来加大对经济发展质量的重视程度有关。

其次，从Luenberger生产率指数看，在TPset下，长三角全要素生产率年均增长率最高的城市分别为无锡、上海和镇江。所有样本城市全要素生产率增长都由技术进步作为主要推动因素。在EPset下，全要素生产率增长最快的为无锡、绍兴和南通。样本城市全要素生产率增长变为由效率改善和技术进步双重驱动，且效率改善的贡献大于技术进步。环境全要素生产率指数比起无约束时出现上升，也主要来自于生产效率改善而不是技术进步。因此结论支持“波特假说”中环境管制可能提高生产效率的论断，但不支持“波特假说”中关于环境管制刺激技术进步的论断，说明长三角地区现阶段环境管制并没有促进技术进步，仍应继续加大环保产业投入，鼓励环保技术研发以及推广应用，持续深化集约型经济转型实践。

1.白雪洁，宋莹.环境规制、技术创新与中国火电行业的效率提升[J].中国工业经济，2009（8）

2.陈诗一.能源消耗、二氧化碳排放与中国工业的可持续发展[J].经济研究，2009（4）

3.李玲，陶锋.污染密集型产业的绿色全要素生产率及影响因素— 基于SBM方向性距离函数的实证分析[J].经济学家，2012（12）

4.林毅夫，刘培林.经济发展战略对劳均资本积累和技术进步的影响[J].中国社会科学，2003（4）

5.潘丹，应瑞瑶.资源环境约束下的中国农业全要素生产率增长研究[J].资源科学，2013，35（7）

6.潘文卿，李子奈.三大增长极对中国内陆地区经济的外溢性影响研究[J].经济研究，2008（6）

7.张慧文.我国三大经济圈金融服务业集群竞争力研究[J].管理世界，2010（6）

8.张军，吴桂英，张吉鹏.中国省际物质资本存量估算：1952-2000[J].经济研究，2004（10）