微弱信号混沌检测系统的噪声分离研究

叶群辉

（福建船政交通职业学院信息工程系，福建福州350007）

微弱信号混沌检测系统的噪声分离研究

叶群辉

（福建船政交通职业学院信息工程系，福建福州350007）

混沌学是目前非线性科学研究中的热点之一.传统的微弱信号混沌检测技术在信号存在噪声的情况下暴露出许多不足之处，如去噪能力较差、检测精度不高等，本文基于前人的研究基础，提出了一种改进小波变换算法的微弱信号混沌检测系统的方法，通过仿真实验可知能够将该方法运用到微弱信号检测.具体方法是对传统小波变换算法的变换域变量进行离散化，目的是消除变换中的冗余，之后采用阈值折衷策略对小波系数进行阈值优化，处理后的小波算法将应用于微弱信号混沌检测系统中，周期策动力为有限离散处理后的含噪信号并入混沌系统，从而实现含噪情况下的微弱信号检测.一系列仿真实验表明，提出和改进的小波变换算法的去噪效果要优于传统小波变换算法，同时在微弱信号混沌检测系统的应用中，改进算法的检测精度和鲁棒性更好.

微弱信号检测；混沌系统；含噪信号；改进小波变换算法；离散优化；阈值折衷策略

0 引言

微弱信号检测是随着工程应用发展而兴起的一门学科，是一种包含了多门综合技术的前沿课题之一.其中微弱信号的意思是信号的强度非常有限，很多信号已经被噪声所淹没.微弱信号检测技术不同于传统的信号检测技术，在传统技术面临了一系列的技术问题的情况下，例如图像信息处理过程中的相位同步问题、传感器的相应信号转换电路和仪表实现方法等[1-3]，它侧重的是如何抑制噪声和提高信噪比，换句换说，微弱信号检测技术是一门专门抑制噪声的技术[4，5].

随着混沌理论的研究逐步深入到临床医学研究、电子保密通讯、电子设备故障检测等领域，许多学者开始致力于把混沌理论应用于微弱信号检测，并且已经取得了一定的成果.至今已报道的关于混沌理论用于检测微弱信号的方法，大多都是利用混沌对具有一定周期的信号产生的敏感性及其对噪声系统的有效免疫力等特点，构造出一种处于混沌状态的非线性系统，从而实现一种对微弱信号的高精度测量[6].混沌理论的微弱信号检测主要有以下3种方法：1）利用已知背景信号，将其作为混沌信号，根据接受信号构建出背景信号的相空间，从而建立预测模型，去掉预测模型中的混沌信号，将淹没在背景信号中的微弱的待测信号检测出来；2）利用混沌理论构建出混沌测量系统，实现对微弱信号的高精度测量.3）在建立一定的混沌系统模型下，将混沌动力学行为处在一种特定的形态下，将待测信号的信息作为补充，利用混沌系统特有的敏感性，通过相空间的变化实现对于噪声比较强的情况的一种微弱信号检测.

随着混沌理论的不断完善以及实践的不断深入，近些年的研究和实践中已经有了比较瞩目的阶段性成果.Lorenz第一次提出在非线性系统中发现混沌现象[7-9]，这之后众多学者经过研究和计算，又在Duffing系统、Chen系统、ADVP系统中发现了混沌现象[10]，充分说明了混沌现象具有普遍性和无穷性.

笔者设计了一种基于改进小波变换的混沌检测系统，主要优势为采用离散优化和阈值折衷策略，以提高其在微弱信号混沌检测系统中的去噪能力.从数值分析角度对在噪声中微弱信号的检测、频率、相位的测量进行讨论.

1 含噪情况下的微弱信号混沌检测系统

混沌系统中的Holmes型的Duffing振子，因具有方程结构简单、阶数低的特点而被广泛应用于微弱信号的检测.Duffing方程为：

在公式中，k为阻尼比，α代表周期策动力幅值，-x+x3代表着非线性弹性力.公式（1）经过一阶微分方程组转化后可以得到以下方程：

对于Duffing混沌系统方程

令t=ωλ，则有x（t）=x（ωλ），并且

将式（4）、（5）代入Duffing方程，得式（7）中的状态方程可以变换为：

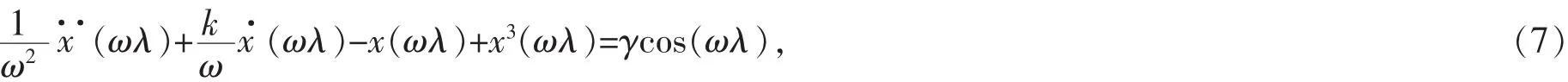
从方程的推导结果可以看出Duffing混沌系统的阈值只与ω有关，但和其他的参数并无关系，如此，若是待测信号进行了变化，只需要改变ω的值即可.

由Melnikov方法求解，其存在混沌的阈值为：

当ω=1 rad/s，k=0.5时，可知r大于0.376 6时，系统处于混沌状态.

用△x（t）表示噪声对x（t）的小扰动，从而得出在噪声存在的情况下系统的微分方程，式（3）变为

采用SPSS 20.0统计学软件对数据进行处理，计数资料以例数（n）、百分数（%）表示，采用x2检验；计量资料以“±s”表示，采用t检验；以P＜0.05为差异有统计学意义。

其中n（t）为噪声，E{n（t）}=0，式（9）减去式（3），由于△x很小，对于△x的高阶项可忽略不计，得

并令c（t）=5x4-3x2，得

将式（12）写成矢量微分方程的形式

其中

其中Φ是系统状态转移矩阵.第1项为暂态解，短时间内衰减为零，所以只需考虑第2项，可得到

由此可见，从统计学的理论上来讲，任何零均值的噪声都不能改变系统原有的运行轨迹，只是会使系统的运动轨迹变粗糙，在理想轨迹上下浮动.

2 微弱信号混沌检测系统的优化

其中：要使逆变换存在，其Fourier变换Ψ（t）要满足允许性条件：

由于Ψ在小波变换中对于其处理信号有观测窗口的作用，即Ψ是1个窗函数，那么Ψ必须属于L1（R），即

从式（20）、（21）可以发现小波函数必然具有振荡性，且当频率为0时，其时域均值亦为0.

由于连续小波变换存在冗余，为了重构信号，有必要针对变换域的变量a，b进行离散化，以消除冗余，其

常简写为：Ψj，k（t）.变换形式为：

WTf（1，k）=〈f，Ψjk〉.

2j2j，

为了能重构信号f（t）保持稳定，要求基小波函数的傅立叶变换满足

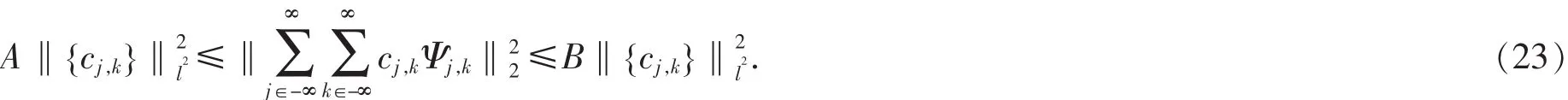
若是对所有二重双无限平方可和序列{cj，k}成立，即对于成立.中，时间尺度a越大，函数的时间分配率越小；在实际中，常取这时假定Ψ是一个R函数，那么存在L2（R）的一个唯一的Riesz基{Ψj，k}j，k∈z，它在意义

上与{Ψj，k}对偶.这时，每个f（t）∈L2（R）有如式（21）的唯一级数表示：

另外，若{Ψj，k}j，k∈z构成L2（R）的规范正交基时，有Ψj，k=Ψj，k，重构公式为：

3 算法性能仿真

对提出的改进算法进行仿真实验以验证效果.本次仿真实验试验在CPU为Pentium（R）Dual-Core T4200 1.2 GHZ，内存为2 GB的PC机上进行.

首先对一般信号分别采用小波变换算法和改进小波变换算法进行去噪处理，结果如图1.

然后将改进的小波变换算法应用于微弱信号混沌检测系统中，图2所示为不含噪的微弱信号，图3所示为含噪的微弱信号，图4所示为基于小波变换的混沌检测系统去噪结果，图5所示为基于改进小波变换的混沌检测系统去噪结果，统计结果如表2所示.

从仿真结果中可以看出，笔者提出的离散优化及阈值折衷的小波变换算法的去噪效果要好于原算法，将其应用于微弱信号混沌检测系统中后，其去噪效果得到很大的提升.

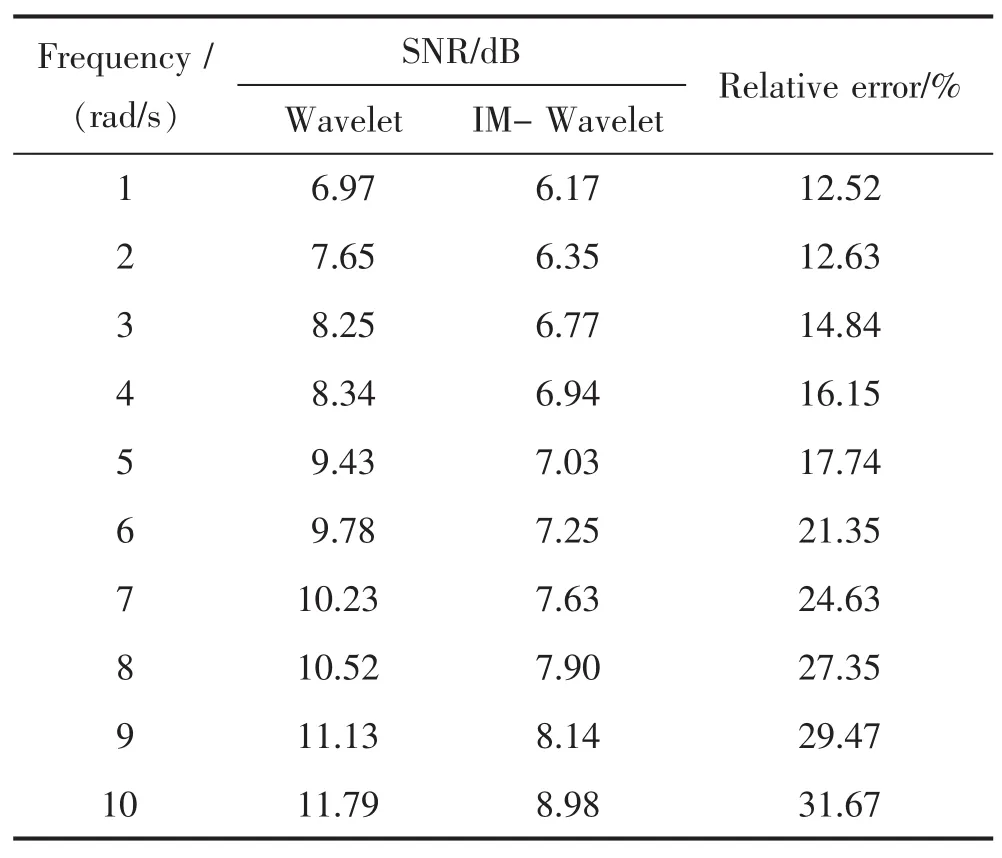
表1 小波变换算法和改进小波变换算法的对比

图1 两种算法的去噪误差对比

表2 微弱信号去噪的误差分析

4 结论

微弱信号检测是一个新兴的领域，它克服了传统意义上基于线性的信号检测技术输入信噪比门限高的缺点.笔者通过对小波变换降噪进行分析，提出基于改进小波变换算法的微弱信号混沌检测系统，进行了仿真实验，通过与传统的降噪方法进行对比，说明了改进后的小波降噪方法的强大优势，其改进策略提高了含噪声微弱信号的检测精度，去噪效果要远远优于原算法.小波变换是一种根据信号和噪声不同特点而进行非线性滤波的一种算法，在改善信噪比的前提下，具有很高的时间分辨率，同时对信号形式不敏感，这是它的一大优势，所以小波变换方法尤其适合微弱信号的检测.随着未来小波理论的不断发展和完善，这一理论在微弱信号检测上的应用也会变得更加广泛.

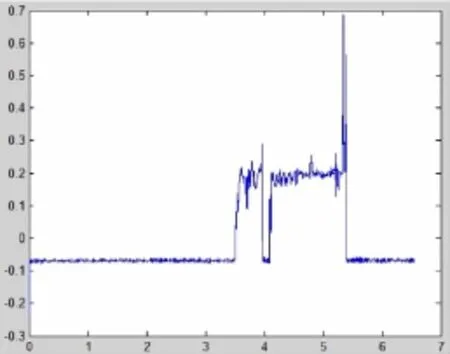
图2 不含噪的微弱信号

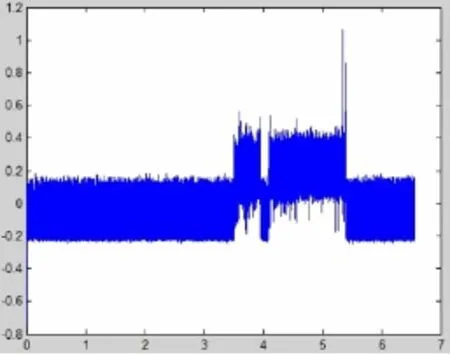
图3 含噪的微弱信号

图4 基于小波变换的混沌检测系统去噪结果

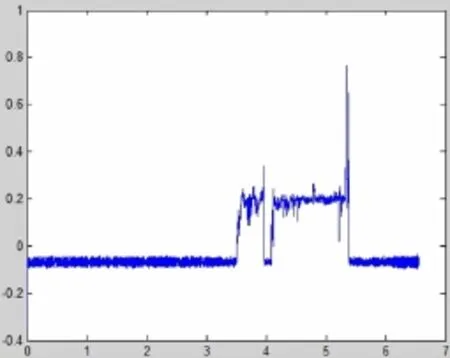
图5 基于改进小波变换的混沌检测系统去噪结果

[1]行鸿彦.消散型同步的微弱周期信号检测及噪声影响分析[J].吉林大学学报：工学版，2014，（4）：1182-1190.

[2]FanJian.NonlinearDynamicsofStochasticResonanceanditsApplicationintheMethodofWeakSignalDetection[J].ActaPhysicaSinica，2014，（11）：111-121.

[3]Pang lili.Research and Development of the Data Collector for Time Domain Aeronautical Electromagnetic Weak Signal[J].Process AutomationInstrumentation，2014，35（4）：83-86.

[4]刘雯.一种用于低频微弱信号采集的通用放大器设计[J].电子科技大学学报，2014，43（2）：222-225.

[5]张弛.基于高速微弱光电探测相关技术的浅析研究[J].科学技术与工程，2014，（8）：182-185.

[6]ZhangGang.ResearchonWeakSignalDetectioninTimeDomainBasedonPhaseLocked Loop and Duffing Oscillator[J].Science TechnologyandEngineering，2014，（6）：13-19.

[7]陈鹏.基于GPU的混沌弱信号检测临界阈值确定[J].计算机应用研究，2014，31（4）：1051-1054.

[8]ZhaoLi.ResearchonChaoticCharacteristicsofaDeformableRosslerSystems anditsUsageforWeakSignalDetection[J].ComputerMeasurement＆Control，2014，22（2）：339-341.

[9]ZongRongfang.WeakSignalDetectionSystemforMarineEnvironmentBasedonLabVIEW[J].InstrumentTechniqueandSensor，2013，（11）：35-37.

[10]高振斌.混沌算法和子空间算法应用在微弱信号检测中的比较[J].科学技术与工程，2014，（1）：235-238.

（责任编辑 李建飞）

Noise Separation From the Weak Signal Detection Chaotic System

YE Qun-hui
（Department of Information Engineering，Fujian Vocational College of Chuanzheng Communications，Fuzhou，Fujian 350007，China）

The traditional weak signal chaos detection system has some technique problems when the signal is with noise，such as poor denoising ability and low detection precision.This paper proposes a novel weak signal chaos detection system based on an improved wavelet transform algorithm.First，the traditional wavelet transform algorithm domain variables are transformed and discretized to eliminate the redundant transform.Then，based on the discrete optimization，the wavelet coefficients are optimized by threshold compromise strategy.The improved wavelet transform algorithm is applied in the weak signal chaos detection system.The noise signal after finite discrete processing is treated as a perturbation of cycle power and put into a chaotic system for detecting weak signal under the noise conditions.The simulation experiments show that the proposed improved wavelet transform algorithm has a better denoising effect than traditional wavelet transform algorithm.Moreover，the improved algorithm shows better accuracy and higher robustness in the weak signal chaos detection system.

weak signal chaos detection system；noisy signal；improved wavelet transform algorithm；discrete optimization

TP393；TN915.02

：A

：1673-1972（2015）06-0047-05

2015-06-16

叶群辉（1971-），女，福建闽侯人，实验师，主要从事网络管理与维护研究.