基于“类比体验”的教学设计

苏建强

一、背景分析

浙教版《数学》七上“一元一次方程的应用（1）”既是对解一元一次方程学习的自然延伸和拓展，也是建构方程、函数模型解决实际问题的起始课，因而该内容的教学设计倍受教师的关注.但通过对大量相关教参、课件及设计的研究发现：一部分设计中，由于教师漠视了对方程建模基本思想方法的归纳和提炼，教学过程成了小学阶段学生学习相应内容的翻版和重复；而绝大部分设计中，因为缺失了学生对“为什么列方程”“怎么列方程”“怎么审题”“为什么要检验”等问题释疑的设计，致使整个教学过程脱离了学生学习的最近发展区.

二、目标定位

（1）在实践探究中通过“类比”理解方程建模的必要性和一般方法，体会模型、类比思想在实际生活中的应用，发展学生的数学概括能力；

（2）通过对不同问题解决的类比、归纳，获得并完善列方程解应用题的初步经验，发展学生综合应用所学知识的能力.

三、教学片段的设计与实践

（一）类比算理悟优劣

设计中通过播放一段有关2014年仁川亚运会的视频，并由嘉嘉和善善的对话引入正题.

活动背景1 中国队在此次亚运会上共获得金牌151枚，银牌108枚，铜牌83枚.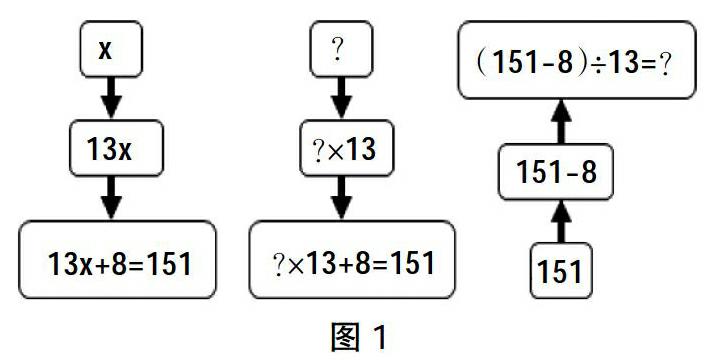

问题1 中国代表队获得的金牌数是印度代表队获得的金牌数的13倍还多8枚，求印度队在本届亚运会上共获得了几枚金牌.

学生很快得到了以下两种列式的方法：

算式法：（151-8）÷13.

方程法：设印度队获得x枚金牌数，由题意可得13x+8=151.

问题2 这两种方法在思考问题的方向上有什么区别？

生：列算式是逆向的，列方程是正向的.

师：让我们一起回忆一下小学里列算式解应用题的一般思路：理清数量关系（如图1，教师结合课件，一边播放一边引导学生分析）.

再倒过来列算式，这时是逆流而上（教师故意放慢语速，并配以自下而上的手势）.而列方程呢，只要用字母表示未知量，顺流而下，省时又省力（教师加快语速，同样配以自上而下的手势）.（略停顿）既然这样，今天我们就选择顺流而下，看看列方程解应用题在初中又会是怎样的呢？（至此新课的导入已是水到渠成）

点评：设计中教师以仁川亚运会中，中国代表队和印度代表队所获奖牌数为背景引入新课，符合七年级学生对新鲜事物充满好奇的心理特点，从而有利于调动学生学习、探究的兴趣.再通过类比两种列式的方法在思维上的异同，辅之以媒体、语速和手势的变化，使学生较直观地感受到列方程的优势所在，既能激起学生自觉选择列方程解应用题的热情，又能促使学生获得方程建模的先行组织者.

（二）类比三量悟分工

活动背景2 嘉嘉、善善两人分别从相距49千米的“新闻中心”和“华城体育场”骑自行车相向而行，嘉嘉比善善提前半小时出发，且每小时比善善少行2千米，当善善出发后2小时两人相遇.

问题3 根据已知条件，我们还可以得到哪些信息呢？

生：（几乎异口同声）可以求嘉嘉和善善的速度；（零星的几个声音）那也可以求他们相遇时所走的路程.

师：那就求一求嘉嘉和善善的速度分别是多少吧！

教师要求学生独立完成，之后引导学生针对解题过程中的问题分析原因，并归纳得列方程解应用题的一般步骤.在此过程之中，学生还展示了不同的设元方法及所列方程.

方法1：设嘉嘉的速度为x千米/小时，可得2.5x+2（x+2）=49；

方法2：设善善的速度为x千米/小时，可得2.5（x-2）+2x=49；

方法3：设嘉嘉相遇时所走的路程为x千米，可得+2=；

方法4：设善善相遇时所走的路程为x千米，可得+2=.

问题4 在行程问题所涉及的三个基本量（速度、时间、路程）中，针对嘉嘉、善善来说哪些是已知量，哪些是未知量？

问题5 这两个未知量在设元和列方程时，分别扮演了哪个角色？

通过对已知条件的分析可知嘉嘉和善善两人相遇时所用的时间是已知量，速度及所走路程是未知量.进而在对上述4种典型解法的类比分析后，不难归纳得到解决行程问题时三个基本量扮演着不同角色，即“一量知，一量设，还有一量列等量”.

点评：在教学设计中，教师没有采用师生共同“分析题意—列方程解题—归纳一般步骤”的常规思路.而是基于学生已有发展水平，采用了学生“体验列方程解题—交流解题思路—归纳一般步骤”的教学策略，充分关注了学生“主体”地位的发挥.在引导学生分析三量间的分工时，教师更以一句“难道，这三量之间还真有分工？”燃起了学生通过“类比”的方法寻求不同方法中所隐含的规律的热情.

（三）类比方程悟本质

正当学生沉浸于发现三量分工的窃喜之中时，教师给出了第6问.

问题6 审题分析有章可循了，列方程有规律吗？有怎样的规律呢？

教师通过引导学生类比上述的方法1、方法3所列方程两边的代数式进行分析，归纳得到列方程的实质是“用不同的代数式表示同一个量，并用等号连结”，列方程的基本方法是“直接列，间接列，两式等号两边立”.

师：（教师指着板书中的4种典型解法）请按照大组序号分别选择对应的设元方法，再列出一个不同形式的方程，并说说方程两边的代数式都表示什么？

片刻之后，学生所列的方程就五花八门地呈现在黑板上了.

方法1：根据相遇时嘉嘉所走路程得2.5x=49-2（x+2）；方法2：根据相遇时善善所走路程得2（x+2）=49-2.5x；方法3：根据嘉嘉的速度得=-2；方法4：根据两人速度差为2得-=2；…endprint

点评：一波未平又起一浪，随着问题6的解决，让原本“眼前一亮”的学生更体会到了数学的“神奇”.随着学生所列的新方程在黑板上令人眼花缭乱地呈现之时，听课教师眼中的“列方程解应用题，会者自会，不会者学也学不会”的“魔咒”不攻自破，学生心中的“数学不难，数学问题的解决是有规律的”之感油然而生.

（四）类比冲突显地位

活动背景3 某天，游泳中心共卖出门票1601张，折合人民币的收入为61639元，全价票为每张40元，折扣票每张为全价票的九折.

问题7 请求出这天游泳中心共卖出全价票几张？

由“活动背景2”的铺垫，大部分学生很快就完成了设元、列方程两个步骤.不一会儿，几个解题速度较快的同学面露“难”色，口中念叨着“老师，怎么票子的张数不是整数？”与此同时，在教室里听课的几个老师也窃窃私语起来.

师：不会吧！票子的张数肯定是正整数，同桌之间互相检查一下，是不是方程列错了，要么是方程解错了，照理不可能有其他原因了.

生：老师，我的做法应该没有问题（声音显得有些不自信）.

师：让我们一起看看这位同学的解法，问题到底出在哪里？

通过师生共同分析发现这位同学的解法的确没有问题，且75%的同学采用了类似的做法.此时教师话锋一转，道明缘由“原来是在网上搜索数据时把总收入的个位数抄错了”，并引出下问.

问题8 请把总收入的个位数改一改，使这天卖出的票数为整数.

随着教室后排的一个声音响起（老师，只要把“9”改成“6”就可以了），教师有意安排的“思维冲突”逐渐进入了收尾小结阶段.

点评：问题解决后的反思向来是学生的一个“弱项”，教师再三强调的“检验”在关键时刻学生还是会“忘了”.在“活动背景2”的解决中，教师只点到为止说明了列方程解应用题要求检验，并没有做过多强调.而在“活动背景3”的解决中，教师却有意安排了一个“错误”营造检验必要性的“氛围”，这样的类比也是本环节设计中独具匠心之处.随着从“6错抄成9”到“9还原成6”（当然，9也可还原成2）的“思维冲突”的形成与“数据修复”的完成，验根反思的必要性也深深映入学生的记忆之中.

（五）类比情境悟通法

问题9 “活动2”“活动3”中问题的解决都用了列方程的方法，类比两活动的背景你能找出它们之间的联系吗（教师在“背景”两字上略加重语气）？

“如果把票子的单价看作是速度，那么票子的张数就是时间……”，学生七嘴八舌地互相补充后，教师如图2点明了这类问题的实质都是a×b=c型的问题.接着教师又如此引导道：“其中三量间的分工，一量知，一量…… ”

点评：数学学习没有一定解题的量的积累就不可能有学生对数学本源的质的感悟，但只有解题而缺少类比、反思的学习将留下的是“入得宝山而空手归”的遗憾.“问题9”的设计不仅给人以在整个教学设计中有“长江后浪推前浪”之感，还让人看到了“轻负高质”“走出题海”的一线曙光.

四、思考

（一）基于学生疑问明确教学重难点

在教学设计中，很多教师都苦于找不到“过人之处”，抱怨自己的课“很难上”.其实，这样的课往往是努力方向最明确、潜在亮点最多的课，学生学习中的疑问就是教学设计中的亮点所在之处.本课设计中，教学始终围绕“为什么要列方程而不用算式”“怎么分析题意、审题”“列方程的一般方法是怎样的”“为什么一定要检验”等问题展开，一环紧扣一环，每一活动的开展都基于之前学生已有的学习经验，自然又不流于形式.

（二）着眼学生能力提升开展类比体验

郑毓信教授曾指出数学就是要让学生“数学地思考问题，用数学的眼睛看世界”.而用数学的思维思考问题，用数学的眼睛看世界的基本方法之一就是“类比”.比较才知事物之间的相同点——联系，比较了才明事物之间的不同点——区别，只有知“联系”明“区别”，才能真正认识事物的本质.本课设计中，从“选择列方程的方法解应用题”到“问题解决中检验必要性的体验”，都以学生亲身经历为切入点，通过营造适合学生实际的教学情境实现“类比”；从“三量之间的分工”“列方程的基本方法”到“不同题型的通解通法”的归纳，无不在学生一次次的观察、类比、猜想与验证中完成. 在一次次的“类比”中，学生的思维得到了发展，能力得到了提升.endprint