科学话《三体》

2015年8月23日，被誉为“中国科幻第一人”的刘慈欣凭借科幻小说《三体》获得“雨果奖”最佳长篇小说奖，这是亚洲人首次获得该奖，也是中国科幻第一次获得世界级的认可。

在小说里，三体叛军通过“三体”游戏向社会传播三体文化，游戏玩家们则通过建立各种模型来躲避乱纪元、预测恒纪元的到来。

游戏第一关，一个文明在“三日凌空”中毁灭，玩家哥白尼成功揭示出宇宙的基本结构；游戏第二关，另一个文明毁灭，它最终证明了三体问题无解，人们放弃了徒劳的努力，并确定全新的走向。至此，游戏的终极目标发生变化，调整为飞向宇宙，寻找新的家园。

《三体》三部曲中有无数让人脑洞大开的经典创意，它们的创作基础就是天体力学中基本的三体模型。那么，究竟什么是三体？

1900年，数学家希尔伯特在一次演讲中提出了23个困难的数学问题以及两个典型例子，第一个是费尔马猜想，第二个就是N体问题的特例——三体问题。对于20世纪数学的整体发展，这两个例子所起的作用远远大于23个问题中的任何一个。最终，费尔马猜想在1994年被美国的怀尔斯解决，而三体问题却一直没有找到答案。

三体问题是天体力学中的基本模型，即探究三个质量、初始位置和初始速度都为任意的可视为质点的天体，在相互之间万有引力的作用下的运动规律。

如图1所示，它们有无数种可能的运动轨迹。最简单的例子就是太阳系中太阳、地球和月球的运动。

在一般的三体问题中，每一个天体在其他两个天体的万有引力作用下，其运动方程都可以表示成6个一阶的常微分方程。因此，一般三体问题的运动方程为十八阶方程，必须获得18个积分才能得到完全解。然而，现阶段还只能得到三体问题的10个初积分，远远不足以解决问题。

我们常说的“三体问题无解”，准确地说是无解析解，即三体问题没有规律性答案，不能用解析式表达，只能算数值解，因此无法得出精确值。然而对于三体问题的数值解，时间会无限放大初始的微小误差，因此数值法几乎无法预测当时间趋于无穷时，三体轨道的最终命运。而这种对于轨道长时间行为的不确定性，就被称为“混沌”现象。

三个物体在空间中的分布有无穷多种情况，由于混沌现象的存在，通常情况下三体问题的解是非周期性的。

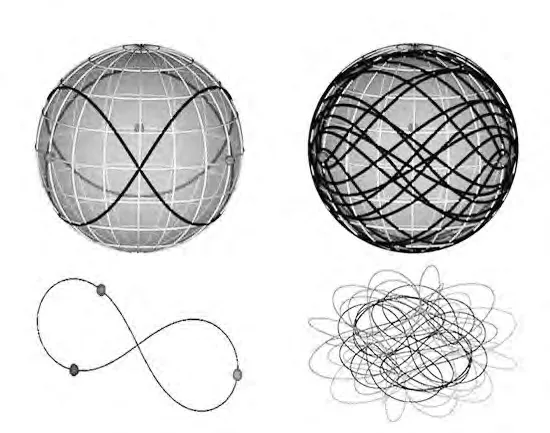
图1

寻找三体问题的通解是枉费力气，但在特殊条件下，一些特解是存在的。然而，必须找到合适的初始条件（位置、速度等），才能使系统在运动一段时间后回到初始状态，即进行周期性的运动。

要发现三体问题的周期性特解绝非易事——自该问题被确认至2013年的300多年中，人们只找到了3族周期性特解。

法国数学家、物理学家约瑟夫·拉格朗日和瑞士数学家、物理学家莱昂哈德·欧拉在18世纪得到了一些结果；20世纪70年代，美国数学家罗杰·布鲁克和法国天文学家米歇尔·赫农借助计算机又得到了更多的结果；1993年，美国数学家、物理学家克里斯·摩尔发现一种奇特现象——特解中3个天体的运动似在一条“8”字形的轨道上互相追逐。

上述所有这些被发现的特解可被归结为下面3族：拉格朗日-欧拉族、布鲁克-赫农族和“8”字形族。

此图为艺术家描绘的从“三星系统”中一颗行星的卫星上看到的情景，这种恒星系统处于极不稳定的混沌运动状态

1772年，拉格朗日在“平面限制性三体问题”条件下找到了5个特解，也就是著名的拉格朗日点。在该点上，小天体在两个大天体的引力作用下能基本保持静止。

比如上面这张图中，地球和太阳的连线上有L1、L2、L3三个拉格朗日点，而在地球轨道上则有L4、L5两个点，它们和太阳、地球构成等边三角形。

L1、L2、L3是不稳定的，如果小天体离开这三个点，就会越跑越远，无法在稳定的轨道上运行，而L4、L5是稳定的。L4、L5的稳定解在太阳系里确实存在实例，如木星的L4和L5点上各有一群小行星，就是著名的特洛伊群和希腊群小行星。

特洛伊群和希腊群小行星

拉格朗日点在深空探测中具有很高的科研价值，主要体现在两个方面：科学观测的极佳位置和深空探测的中转站。

位于L4和L5的航天器能与两个天体保持相对静止，有利于一些长期的科学观测。而共线拉格朗日点存在稳定流形与不稳定流形，使得航天器在其上运动时，可不需耗费任何能量地趋近或远离周期轨道，这一点能为设计行星间的转移轨道提供巨大帮助。

布鲁克-赫农族的解比较复杂，两个天体在里面横冲直撞，第三个天体在它们外围作环绕运动。

目前三体问题的研究主要集中在“限制性三体问题”上

直到2013年，塞尔维亚物理学家米洛万·舒瓦科夫和迪米特拉·什诺维奇发现了新的13族特解。他们在著名学术期刊《物理评论快报》上发表论文，描述寻找特解的方法：用计算机模拟，先从一个已知的特解开始，然后不断对它的初始条件进行微小调整，直到新的运动模式被发现。这13族特解非常复杂，在抽象空间“形状球”中，就像一个松散的线团。

三体问题特解的族数扩充到了16族，这一新发现令科学界欢欣鼓舞，其成果加深了人们对天体运动的了解，促进了天体力学和数学物理的进一步发展，尤其是对人们研究太空火箭轨道和双星演化很有帮助。