基于Bayes估计的离散Kalman滤波相关观测融合*
2015-12-26钱志龙许百如
杨 红 彭 军 钱志龙 许百如
(广州大学物理与电子工程学院,广州,510006)
基于Bayes估计的离散Kalman滤波相关观测融合*
杨 红 彭 军 钱志龙 许百如
(广州大学物理与电子工程学院,广州,510006)
针对带相关观测噪声和带不同未知观测函数的多传感器离散系统,在已有的融合算法基础上提出了基于Bayes估计的加权最小二乘(Bayes estimation weighted least squares,BYEWLS)分布式融合Kalman滤波算法。该方法充分利用未知参数的验前信息,以风险函数为评价指标,证明了BYEWLS融合算法优于WLS融合算法,针对BYEWLS融合算法是有偏估计,提出了在线消除偏差的方法。分布式融合算法减少了计算负担,提高了融合精度,便于实时应用。最后通过仿真例子验证了该方法的有效性和理论分析的正确性。
离散系统;Kalman滤波;分布式观测融合;Bayes估计
引 言
信息融合是对来自多个信息源的数据进行检测、相关、组合和估计处理,从而得到比任何单一信息源所获得数据更多的有用信息,它一般用于对目标的检测、定位、跟踪和识别。对于基于Kalman滤波的多传感器观测数据融合,主要有状态融合和测量融合,测量融合可分为集中式融合和分布式融合[1-10]。通常,用集中融合方法得到的观测方程的观测向量维数远大于用加权观测融合方法得到的融合观测方程的观测向量维数,因此计算负担增大,不便于实时应用,而采用加权观测融合方法可明显减少计算负担,便于实时应用。文献[2]对带相同观测阵和带不相关噪声的多传感器系统证明了加权观测融合Kalman滤波算法功能等价于集中式融合Kalman滤波算法;文献[4]对带相关观测噪声的多传感器系统用Lagrange法[11]提出了一种加权观测融合Kalman滤波算法,并用信息滤波器证明了它功能等价于集中式融合Kalman滤波算法,但其局限性是仍假设所有传感器具有相同的观测阵;文献[8]对带不同观测阵和带相关观测噪声的多传感器系统用不同于文献[4]的加权最小二乘(Weighted least squares,WLS)[11]法提出了两种新的加权观测融合稳态Kalman滤波算法,并用稳态信息滤波器证明了它们功能等价于集中式稳态Kalman滤波算法。本文研究了观测矩阵未知的情况下,具有不同观测函数和带相关观测噪声的多传感器离散系统的相关观测融合问题:(1)利用未知参数的验前信息,对观测方程中未知的观测矩阵进行估计,并在此基础上提出新的分布式融合时变Kalman滤波算法(Bayes estimation weighted least square,BYEWLS);(2)分析了BYEWLS融合算法的性质,基于观测方程矩阵估计的有偏性,提出在线纠正偏差的方法,该方法简单实用;(3)应用风险函数为评价指标证明了BYEWLS融合算法优于WLS融合算法。
1 问题描述
带多传感器的带不同观测阵的离散多传感器系统模型可以描述为

(1)
(2)
式中:t为离散时间,x(t)∈Rn为状态,yi(t+1)∈Rmi为第i个传感器在t+1时刻的观测值,vi(t)∈Rmi为第i个传感器在t时刻的观测噪声,w(t)∈Rr为输入白噪声;F为状态转移矩阵;Hi为观测矩阵;G为干扰输入矩阵。
假设1w(t)∈Rr和vi(t)∈Rmi(i=1,…,L)为零均值不相关高斯白噪声,且vi(t)和x(t)不相关,vi(t)和vj(t)(i≠j)是相关观测高斯白噪声,有
(3)
式中:E为均值符号,δtt=1,δth=0(t≠h),Q>0。
假设2 存在非奇异的矩阵,HT(t)R-1(t)H(t),定义
(4)
(5)

2 基于Bayes估计的不同观测阵加权最小二乘分布式算法
贝叶斯理论提供了一种计算假设概率的方法,基于假设的先验概率,给定假设下观察到不同数据的概率以及观察到的数据本身来计算后验概率,一般地,设θ为未知参数(可以为向量),它的验前密度记为π(θ),Y为观测量,于是在获得观测量之后,θ的验后密度由Bayes公式给出[12]
(6)
式中:f(Y/θ)为θ给定时Y的概率密度函数,Θ为θ的参数空间。在进行Kalman滤波融合时,考虑模型参数本身的先验信息条件,应用贝叶斯估计可以提高融合精度。

(7)
(8)
(9)

3 基于Bayes估计的带不同观测阵的分布式观测融合Kalman滤波算法
可对式(2)的L个观测方程进行观测融合,本文采用基于Bayes估计方法对观测方程进行观测融合。合并式(2)的L个观测方程可以得到集中式观测融合方程
(10)
其中
(11)
(12)
且有
(13)
故有白噪声v(1)(t)的方差阵为
(14)
式(14)也可以写成融合观测方程
(15)
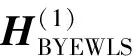
4 基于BYEWLS估计的分布式观测融合Kalman滤波算法
首先讨论样本的极限特性,注意到
而
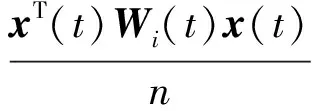
(16)

为了纠正偏差,本文针对多传感器系统偏差的动态补偿问题,提出了一种偏差的在线补偿算法,即在计算E(Hi,BAYES(t+1))时取
(17)
将式(17)代入式(16),用式(16)来消除Hi,BAYES(t+1)估计值的偏差。但从统计决策的观点来看,对于无偏的要求并不总是必要的,而可以用下列的概念来评价融合算法。
定义1 设Z为随机向量,分布依赖与未知参数向量θ,记d(Y)为θ的一个估计,这里Y表示Z的样本。记L[θ,d(Y)]为非负函数,它表示真实参数为θ,而以d(Y)作为它估计时引起的损失,称为损失函数。令
(18)
它表示真实参数为θ时,关于Y的分布所取的期望值,称R(θ,d)为风险函数。如果对所有θ满足
(19)
则称估计d1至少和d2一样好。如果∀θ,则
(20)
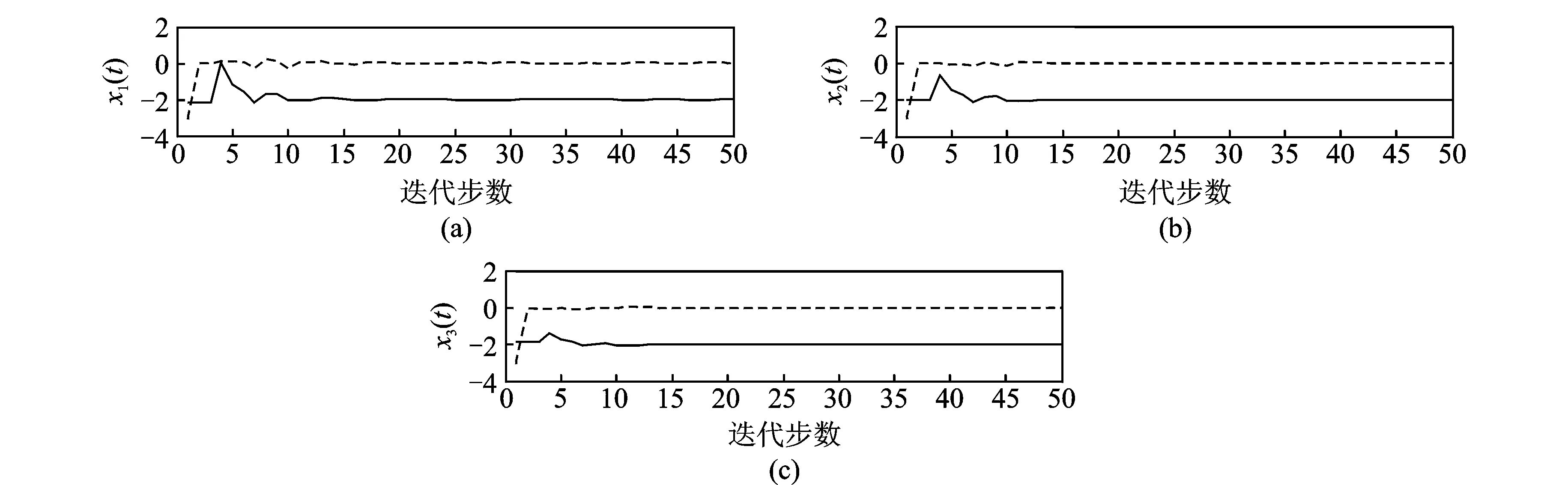
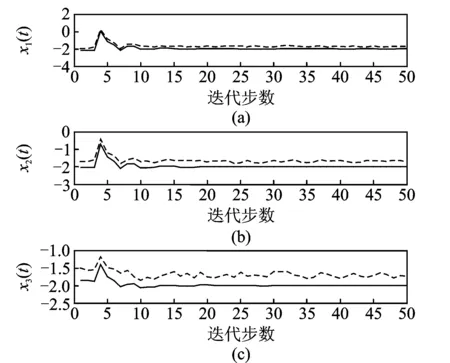
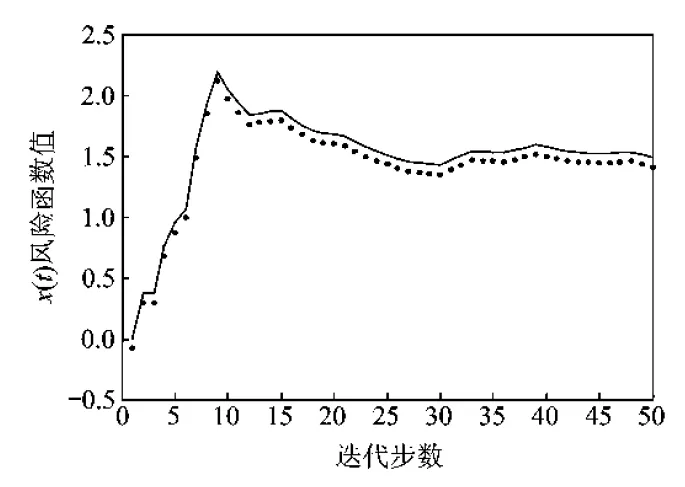
以及R(θ,d1) (21) 此时 (22) 本文将风险函数作为评估估值好坏的标准。 因此用式(7)估计出来的Hi,BAYES值方差阵小于用WLS方法估计出来的Hi,WLS值的方差阵,根据定义1,即为Hi,BAYES值优Hi,WLS值。 定理2 离散多传感器系统式(1)和(2),用BYEWLS法所得到的分布式观测融合时变Kalman滤波器优于用WLS法所得到的分布式观测融合时变Kalman滤波器(证明见附录)。 5.1 三状态系统仿真 例1 考虑带相关观测噪声的三传感器跟踪系统 (23) (24) BYEWLS融合算法有偏差,这种偏差是系统偏差,需要校正。本文依据多传感器提供的测量和跟踪信息,形成测量数据对,当采样周期到时,利用已测量数据纠正系统偏差,补偿和修正数据,实现多传感器的融合跟踪。图1是用Bayes估计计算出的3个观测方程中的观测矩阵与实际的观测矩阵相减,再将差值矩阵求迹得到的结果,图1(a,b,c)分别是第1,2,3个观测方程。图中实线是未纠偏时的差值矩阵的迹,虚线是纠偏后的差值矩阵的迹,可以看出用式(17)来在线消除偏差,可以得到比较好的效果,纠偏后估计的观测矩阵和实际的观测矩阵误差非常小。 为了进一步验证BYEWLS的优点,表1列出了真实的状态值以及利用观测方程估计出来的状态值,估计值分别用BYEWLS和WLS算法估计,并且BYEWLS算法又分纠偏和未纠偏两种。根据定义1,计算3种算法的风险函数值如图2所示,图中虚线是根据WLS算法计算出来的,实线是未纠偏的BYEWLS算法计算的,点线由纠偏后的BYEWLS算法计算,从中可以得出BYEWLS算法要优于WLS算法,而BYEWLS算法进过纠偏后其估计值更接近实际值。 图1 基于Bayes估计计算的观测矩阵与实际的观测矩阵之差的迹Fig.1 Matrix trace of difference based on Bayes estimation matrix and actual observation 时间t真实值应用BYEWLS计算(纠偏)应用BYEWLS计算(未纠偏)应用WLS计算x1(t)x2(t)x3(t)x1(t)x2(t)x3(t)x1(t)x2(t)x3(t)x1(t)x2(t)x3(t)10.00.01.0-0.34168-0.341680.64302-0.34372-0.343720.62281-0.54050-0.41908-06.203920.0273270.402330.90233-0.286750.197650.84352-0.223420.131840.60552-0.226490.128040.6315930.402330.902330.902330.216530.924090.924090.110050.556650.556650.109080.578350.6133640.122310.49731-0.002680.219730.325230.184570.811641.28050.655350.922641.54020.8908850.997310.99731-0.002690.924260.924260.366143.09693.09690.652152.87352.65970.65409︙︙︙︙︙︙︙︙︙︙︙︙︙47263.121.599-0.40088263.0122.6460.74994263.0122.6520.75538264.3122.760.7533248274.7222.099-0.40088274.6323.1480.75009274.6423.1540.7553275.9323.260.7533349288.6524.6491.6494288.6924.21.1573288.6924.2011.158329024.3061.156450300.7725.1491.6494300.8124.6991.1572300.8124.71.1581300.2624.6521.1549 图2 根据估计的观测矩阵计算出来的x(t)风险函数值Fig.2 Risk function values of x(t) calculated by estimated observation matrix 5.2 九状态系统仿真 例2 将例1中状态方程的状态数目由3个增加到9个,观测方程数目不变 (25) (26) 图3是例1和例2估计结果的比较,都是用Bayes估计计算出来的3个观测方程中的观测矩阵与实际的观测矩阵相减,再将差值矩阵求迹而得。图3(a,b,c)分别是第1,2,3个观测方程,图中实线是例1未纠偏时的差值矩阵的迹,虚线是例2未纠偏时的差值矩阵的迹,比较可以得出例2的偏差比例1的要小。图4是用例1和例2估计出来的状态值计算出的风险函数值,图中实线属于例1,点线属于例2,也可以得出例2要优于例1。 图3 例1和例2计算3个观测矩阵与实际的观测矩阵之差的迹 Fig.3 Matrix trace of difference between three calculated observations matrix and actual observation matrix with Case 1 and Case 2 图4 根据例1和例2估计的观测矩阵计算出来的x(t)风险函数值 Fig.4 Risk function values ofx(t) calculated by estimated observation matrix with Case 1 and Case 2 数据融合的目的是要提高数据估计精度和可靠性。具有不同观测函数和带相关观测噪声的多传感器离散系统通过多种融合方式,能提高Kalman滤波器的精度。对于不同的观测融合方式,从风险函数的角度考虑,BYEWLS分布式融合方式要优于WLS分布式融合方式。虽然BYEWLS融合算法是有偏估计,但可以通过在线消除偏差的方式来克服。 [1] 李鹏飞,黄建军,黄敬雄,等.一种模糊Kalman滤波机动目标跟踪的新算法[J].数据采集与处理,2009,24(4):483-486. Li Pengfei, Huang Jianjun, Huang Jingxiong, et al. Fuzzy Kalman filter for maneuvering target tracking [J]. Journal of Data Acquisition and Processing, 2009, 24(4): 483-486. [2] 徐琦,蔡聪,王熠钊.一种基于数据融合的机动目标跟踪预测算法[J].系统仿真学,2011,23(11):2444-2448. Xu Qi, Cai Cong, Wang Yizhao. Forecast algorithm for tracking moving targets based on data fusion [J]. Journal of System Simulation, 2011, 23(11): 2444-2448. [3] 陶贵丽,邓自立.含未知参数的自校正融合Kalman 滤波器及其收敛性[J].自动化学报,2012,38(1):109-119. Tao Guili, Deng Zili. Self-tuning fusion Kalman filter with unknown parameters and its convergence [J]. ACTA Automatica Sinica, 2012, 38(1): 109-119. [4] 欧连军,丘红专,张洪钺.多个相关测量的融合算法及其最优性[J].信息与控制,2005,34(6):690-695. Ou Lianjun, Qiu Hongzhuan, Zhang Hongyue. Multiple correlated measurements fusion algorithm and its optimality [J]. Information and Control, 2005, 34(6): 690-695. [5] Schopp P, Klingbeil L, Peters C, et al. Design, geometry evaluation, and calibration of a gyroscope-free inertial measurement unit[J]. Sensors and Actuators A: Physical, 2010,162(2): 379-387. [6] Murshed A M, Huang B, Nandakumar K. Estimation and control of solid oxide fuel cell system[J]. Computers and Chemical Engineering, 2010, 34(1): 96-111. [7] 王宏建,王晶,刘振业.基于迭代扩展 Kalman 滤波建议分布和线性优化重采样的快速同步定位与构图自校正加权观测融合Kalman估值器[J].电子与信息学报,2014,36(2):318-324. Wang Hongjian, Wang Jing, Liu Zhenye. Fast simultaneous localization and mapping based on iterative extended Kalman filter proposal distribution and linear optimization resampling [J]. Journal of Electronics & Information Technology, 2014, 36(2): 318-324. [8] 王小旭,梁艳,潘泉,等.带有色量测噪声的非线性系统Unscented卡尔曼滤波器[J].自动化学报,2012,38(6):986-997. Wang Xiaoxu, Liang Yan, Pan Quan, et al. Unscented Kalman filter for nonlinear systems with colored measurement noise [J]. ACTA Automatica Sinica, 2012, 38(6): 986-997. [9] 杨柳庆,肖前贵,牛妍,等.基于渐消卡尔曼滤波器的定位系统设计[J].南京航空航天大学学报,2012,44(1):134-138. Yang Liuqing, Xiao Qiangui, Niu Yan, et al. Design of localization system based on reducing Kalman filter[J]. Journal of Nanjing University of Aeronautics &Astronautics, 2012, 44(1): 134-138. [10]耿剑,张玲华.一种基于修正卡尔曼滤波的蜂窝定位算法[J].数据采集与处理,2013,28(2):201-206. Geng Jian, Zhang Linghua. Cellular location method based on modified Kalman filter [J]. Journal of Data Acquisition and Processing, 2013, 28(2): 201-206. [11]Kailath T,Sayed A H,Hassibi B. Linear estimation[M].New Jersey:Prentice-Hall,2000:44-99. [12]张金槐.线性模型参数估计及其改进[M].长沙:国防科技大学出版社,1999:11-23. Zhang Jinhuai. Parameter estimation of linear model and improvement[M]. Changsha: National University of Defense Technology Press, 1999: 11-23. [13]赵树杰,赵建勋.信号检测与估计理论[M].北京:清华大学出版社,2004:425-440. Zhao Shujie, Zhao Jianxun. Signal detection and estimation theory[M]. Beijing: Tsinghua University Press, 2004: 425-440. 附录: 证明: 记Δ=Var(Hi,WLS(t))-Var(Hi,BEWLS(t)),要证明Δ≥0,为此只要证明对∀η≠0,有 (A1) 或者对∀η≠0,有 (A2) (A3) 由于 (A4) 而且 (A5) 因此ηTΔη≥0,对所有η≠0成立。于是有 (A6) 这说明用式(7)估计出来的Hi,BAYES值方差阵小于用WLS方法估计出来的Hi,WLS值的方差阵,根据定义1,即为Hi,BAYES值优Hi,WLS值。 定理2 离散多传感器系统式(1)和(2),用BYEWLS法所得到的分布式观测融合时变Kalman滤波器优于用WLS法所得到的分布式观测融合时变Kalman滤波器。 证明:由于在t时刻,x(t)已知,故应用文献[12]的方法,有 (A7) 应用定理(1),有 (A8) 由于(x(t)xT(t))>0,可得 (A9) Correlated Measurement Fusion of Discrete Kalman Filtering Based on Bayes Estimation Yang Hong, Peng Jun, Qian Zhilong, Xu Bairu (School of Physics and Electronic Engineering, Guangzhou University, Guangzhou, 510006, China) Under the multi-sensor discrete system with correlated measurement noises and different unknown measurement functions, the distributed fusion Kalman filtering algorithm is proposed according to the existing fusion algorithms based on Bayes estimation weighted least squares (BYEWLS). The algorithm makes full use of the prior information for the unknown parameters. BYEWLS algorithm gains an advantage over WLS algorithm according to risk function. Meanwhile, the on-line method is proposed to eliminate the bias emerged with BYEWLS fusion algorithm. The distributed fusion algorithms can reduce the computational burden and improve the fusion accuracy, therefore they are suitable for real-time applications. As a result, the simulation example indicates the validity of the theory analysis. discrete system; Kalman filtering; distributed measurement fusion; Bayes estimation 国家自然科学基金(51078093)资助项目;广东省科技计划(2011B010300026)资助项目。 2013-06-21; 2014-06-09 O211.64 A 杨红(1967-),男,博士,副教授,研究方向:非线性控制、信息处理,E-mail: yhenryh@sina.com。 许百如(1971-),女,实验师,研究方向:信息处理。 彭军(1973-),女,高级实验师,研究方向:光信息处理。 钱志龙(1975-),男,实验师,研究方向:光信息处理。
5 仿真分析与结果
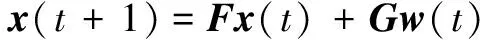

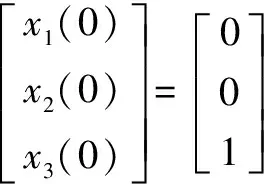



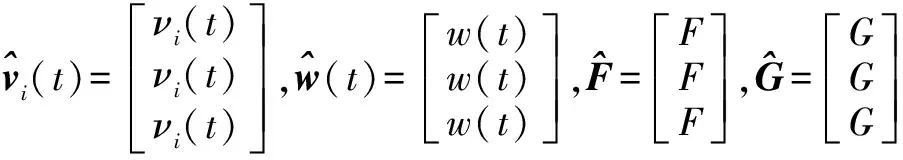
6 结束语