大数据关联关系度量研究综述*

2015-12-26钱宇华成红红梁新彦王建新

数据采集与处理 2015年6期

关键词：度量数据挖掘关联

钱宇华成红红梁新彦王建新

(1.山西大学计算智能与中文信息处理教育部重点实验室,太原，030006; 2.山西大学计算机与信息技术学院，太原，030006)

大数据关联关系度量研究综述*

钱宇华1,2成红红1,2梁新彦1,2王建新1,2

(1.山西大学计算智能与中文信息处理教育部重点实验室,太原，030006; 2.山西大学计算机与信息技术学院，太原，030006)

大数据关联性分析是大数据挖掘的基础，一个好的关联性度量是实施关联分析的关键。本文首先指出大数据时代关联度量面临的挑战和研究现状，从关联关系度量的构造角度出发，对现有的关联关系度量进行整理，归纳总结了这些关联关系的性质和适用条件。在回顾关联度量发展历程的基础上，结合大数据时代关联关系的特点，提出构造关联度量可能满足的条件。最后针对多模态数据关联关系度量的若干问题进行探讨和梳理，从3个角度出发，提出应对多模态数据空间转换的挑战，以引起对该领域更深入的思考与研究工作，从而促进大数据挖掘工作的进展。

大数据；关联性分析；关联度量；多模态数据

引言

信息技术的飞速发展，尤其是社交网络、云计算和物联网等信息获取技术的进步，全球数据量以每两年翻倍的速度增长和积累，大数据愈来愈得到人们的关注，已是具有国家战略意义的新兴产业[1]。从各种各样巨量数据中快速提取有价值的信息和获得潜在的事物规律是大数据挖掘的主要任务之一[2]。正如美国加州大学伯克利分校Speed 教授在《Science》杂志上发表论文所述，从庞大数据集中发现数据之间潜在的重要有趣的关系变得十分重要，21世纪将是关联性学习的时代[3]。所谓关联性学习就是发现存在于大量数据集中的关联关系或相关关系，从而描述一个事物中某些属性同现的规律和模式。这种同现关系可能表现为具有严格确定性的函数显示表达形式，也可能是客观对象之间确实存在，但在数量上不是严格对应的依存关系，也可能是完全不存在内在联系的虚假相关关系[4]。关联分析渗透到机器学习、生物信息学、神经科学、经济与金融、社会网络、多媒体以及大气学数据挖掘等科学研究的各个领域[5-7]。在网络查询中，搜索引擎根据用户搜索内容与互联网中内容的相关性进行推荐[6]；在遗传学中，研究物种与物种之间有相关性的基因、功能及其变异、传递和表达规律[8]；在气象学中，通过分析场与场之间的相关性短期预测未来气候[9]。但是在大数据时代，数据量的大量积累使得数据关联形式多种多样，不同领域需要挖掘更重要和更符合实际的关联关系形式，因此清晰刻画所研究对象的关联关系及关联强度是大数据挖掘和应用的重要研究方向之一[10]。

数据的大量产生为数据挖掘提供了丰富的资源，尤其是给描述对象提供了新的见解。如何从TB级及以上的数据集中成功探索数据的意义是大数据时代中重要的问题。要探索大型数据集中的科学问题，为解释新问题和给出建议方式，必须找到意想不到的模式和解释证据。大数据表现出的大规模性、多模态性和混杂性等特征是大数据挖掘与知识发现面临的主要挑战。Liang和Qian等提出用粒计算的理论和方法解决大数据挖掘所面临的问题，并指出多粒度模式发现和融合是处理大数据大规模性、多模态性、混合性特征的自然要求，局部数据粒上的模式发现和多粒度关系发现是支撑大数据应用的重要方面之一，也即信息的合理粒化将是实现这一目标的重要手段，而关联分析是实施这一手段的首要基础[11]。聚类分析是数据挖掘中重要的技术手段之一，用于探测数据的抱团性。聚类的核心是找到刻画数据对象(可以看作向量)之间远近的距离，构造相似性矩阵。聚类分析是一种启发式的探索数据结构的方法，因此相似关系可以通过关联关系的度量来刻画，信息粒化实施的核心也是对象间关联关系的度量[12]。分类也是机器学习和数据挖掘中重要的学习问题，发现特征空间与决策空间的依赖性是关键。在特征选择、特征约简与多标签学习等研究中，通常需要找到合理的判断冗余性和相关性的指标，这些指标也可以通过关联关系的度量来刻画[13]。关联关系的发现是支撑大数据应用的重要方面之一。在大数据关联关系挖掘中，关联关系不再仅限于线性关系和常用的特殊函数形式，还有可能是特征间不确定性、分布相似性、或者是特征某些取值的同现性[11]。例如在基因表达中蛋白质的形成受多个基因控制形成，希望找到这些基因之间的联合作用关系，但预先不知道数据分布的先验分布需要采用探测性的分析方法，需要先找到一种刻画这些关系的度量，根据这个度量取值的大小判断关系的重要性进行下一步研究。

因此在大数据挖掘中，关联关系的度量经常是各个研究的基础。大数据中多种复杂关系并存，而且非线性关系与线性关系同等重要，传统的偏向识别线性关系的Pearson相关系数、偏向识别单调函数的Spearman相关系数和Kendall相关系数已经不能很好地适用于大数据时代关联分析的研究[14-15]。因而从大规模数据中探索复杂关系变成热点研究课题，关联关系的发现和关联关系测度的刻画及选择显得尤为重要，新的适应于大数据要求的关联关系度量新范式亟待提出。本文首先梳理了大数据关联分析面临的挑战及研究现状，再回顾已有相关关系的构造方法和适用条件，以期对大数据关联关系度量新范式提供启示，并指明应对大数据变量间关联度量挑战，度量新范式可能满足的条件。最后进行总结与展望。

1 大数据关联关系度量的挑战与现状

1.1 大规模性

数据规模的急剧膨胀给数据挖掘尤其是互联网数据挖掘带来巨大的挑战。大数据时代获得的数据量呈现大规模性，大规模性不仅表现在样本量大，还表现在数据的维度高，变量间的关联模式也会增多从而表现出关联关系多样性。除了传统的线性关系，常见的单调变化函数之外，需要刻画层出不穷的数据关联形式。在经济金融研究中，时间序列数据的分布相比正态分布往往呈现厚尾尖峰现象，这种分布形式的数据关联用传统的Pearson相关系数已不适用[16]；在信号处理系统中，脉冲信号呈现正弦波或余弦波，甚至是混合波形式，这种非线性关联关系的刻画使得传统相关系无能为力[17]。而在大数据集中，多种关联关系经常会同时出现，需要关心的是从众多关联关系中挖掘出具有强关联的变量对，从而在该关联度量下选择排序靠前变量对进行分析。因此，如何准确刻画不同形式的关联关系，并从多种复杂关联中选取关联强度大的变量对研究变得至关重要[10]。基于随机变量特征函数的性质，Székely于2007年提出用距离相关系数(Distance correlation,dCor)考察两个任意维随机向量之间的关联系数，且能有效识别各种关联模式[18-19]；Lopez-Paz等对数据进行非线性映射然后再求最大典型相关系数，不仅能识别线性关系还能识别非线性关系[20]；因为中心极限定理中多个独立变量的和具有高斯性所以提出基于非高斯性的依赖性度量以能识别数据中多种关联形式[21]。

1.2 多模态性

通过不同的方法或角度描述同一个事物，将这个方法或视觉称为一个模态。如视频数据挖掘中，视频可以分成字幕、音频和图像，它们从不同视觉描述了视频所要表达的信息。大数据往往由大量源头产生，而且常包含图像、视频、音频、数据流、文本和网页等不同的数据格式，因此其模态是多种多样的，每个模态都为别的模态提供一定的信息，模态之间具有一定的相关性，利用模态之间的共有信息探求它们之间的潜在规律是多模态数据挖掘的关键。已经有关于定矩变量、定序变量和定类变量等同模态变量之间的相关性度量公式，也有基于小样本情况下在混合变量之间的相关性度量研究[22]，但是在大数据背景下不同模态变量间关联性分析仍是个值得研究的问题。不同模态之间的信息互为差异、互相补充。典型相关分析(Canonical correlation analysis, CCA)是传统分析多元变量组间线性相关关系的方法，为了探索变量组间的非线性关联关系，文献[23]将变量数据进行核变换之后再利用线性分析方法度量变量组间的相关关系(Kernel canonical correlation analysis, KCCA)。2011年，Reshef等在《Science》提出了挖掘大数据新颖关联的方法，认为如果两个变量之间存在关联，则在变量的散点图上施加一个网格可以将关联关系压缩出来，并称该度量具有普适性和均衡性，而且适用于混合数据分布[10]。

1.3 动态性

大数据的另一显著的特点就是数据随着时间快速积累，迅速增长，变量间关联关系表现出一定的动态性。比如在社会网络中，大量节点上的状态不断发生变化，节点之间的链接情况不断发生变化，节点之间的关联关系也随时间发生关系，给面向社会网络数据挖掘的实时性要求带来挑战[6]。在股票交易市场中，数据在交易期内每一秒都在发生变换，如何及时有效地做出组合优化决策降低投资风险至关重要[24]。Bandt提出一种分析大数据时间序列的自相关函数形式，能够识别关系变化中的噪声从而进行有效预测[25]。

1.4 价值密度低

张钹院士说：大数据是矿石，需要经过提炼才能使用[26]。巨大的变量不一定都要使用，以视频数据为例，连续不断监控过程中，有用的数据可能只有一两秒。如何从大量的数据中选择有价值的数据成为重中之重。因此变量约简或选取有价值变量变得尤为重要，变量间关联度量是实施这一目标的核心。

数据的价值密度低也表现在数据的噪声量多，噪声的产生可能与产生数据的主体有关，也可能与数据采集手段和存储方式有关。噪声量积累过多，噪声关系可能掩盖真实变量的关系。如果噪声呈现一定的规律，会导致变量间存在伪相关关系，如果噪声比较混乱，原本关联性较强的变量可能会被噪声抵冲。前者就像在一个大城市里，有两个长得特别像的人但他们实际没有基因关系；后者就像在偌大的城市里遇到了一个熟人[4]。因此，大数据挖掘中构造的关联强度度量还需对噪声有一定的识别作用。Reshef等提出最大信息系数(Maximal information coefficient, MIC)的同时指出关联度量应该具有均衡性。均衡性的提出“可谓一石激起千层浪”。Kinney和Atwal 给出了Reshef文章中提到的R2均衡性的严格数学定义，进一步提出自均衡性定义，称MIC不满足自均衡定义，基于信息论的基本互信息度量满足自均衡性[27]。Ding 等认为基于互信息的关联度量都不满足均衡性，因为互信息不能准确估计，认为一个均衡性的关联度量应该反映背景噪声中由数据决定的信号强度，利用copula连接函数的性质并从数学上给出混合copula均衡性的定义，据此提出能够深入挖掘变量间关联信息的copula相关系数[28]。

综合上述分析可知，大数据大规模性、多模态性、动态性和价值密度低等特性给大数据变量间关联关系的度量带来的挑战是多方面、多层次的。这些挑战需要在已有的研究基础上，以全新的视角发展大数据的关联关系度量，推动大数据学科的发展和应用。

2 现有关联关系度量的构造及适用条件

关联和相关是解释两个统计变量之间关系的方法，都是相对于独立性而言的。关联关系是一个更通用的术语，相关可以看作是关联的一种特殊情况，主要度量实际上是线性关系的变量对。本文讨论包括线性关系的所有关联关系度量系数，因此全文统称关联关系度量。本节回顾关联关系度量的构造思路，一种是基于消减误差比例(Proportional reduction of error, PRE)原理：运用变量的集中趋势和离散趋势构造；另一种是基于独立性检验构造。前者趋向去发现变量间的线性关系，后者旨在识别除独立之外的其他关系。

2.1 基于PRE原理的关联关系度量

19世纪80年代，Galton在研究人类身高遗传问题时首次提出了相关的概念[29],1990年Karl Pearson在Galton的相关研究基础上提出Pearson相关系数，它是最简单的线性相关系数，用于衡量定矩变量间线性相关程度。此后经过一个多世纪的发展，相关系数有了较为完整的理论基础和广泛的应用领域[30]。协方差是衡量两个变量间线性关联程度的特征数，为了消除量纲的影响，对协方差除以相同量纲的量就得到了相关系数，也称Pearson积矩相关关系。

(1)对称性：ρ(X,Y)=ρ(Y,X)，r(x,y)=r(y,x)。

(2)正仿射不变性：ρ(X,Y)=ρ(aX+b,cY+d)，其中a,b>0,a,b,c,d∈R。即两个变量分别经过位移和尺度的变化，相关系数保持不变。

但是Pearson相关系数的准确度量易受奇异值的影响，为了剔除影响数据整体关系的干扰因素，将主体相关性比较客观地计算出来，心理学家Spearman提出的Spearman秩序相关系数[15]。可用于评估两个连续变量或次序变量之间的单调关系。在单调关系中，变量变化具有同步性，但是不一定按不变的比率变化。Spearman相关系数与Pearson相关系数不同，是基于每个变量对的秩序值而非原始数据。

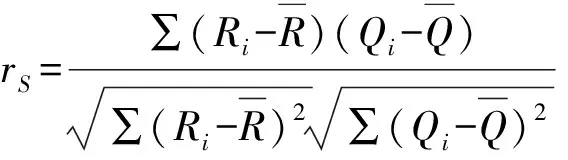
(1)对称性：rS(x,y)=rS(y,x)，τ(x,y)=τ(y,x)。

(2)单调增变换不变性：数据点在进行增变化时，不管是线性的还是非线性增变化，只要满足数据点的相对秩不变，相关系数就不变。单调减变换不会改变关联强度但会改变关联的方向。

(3)稳健性：异常数据点对线性相关系数的影响比较大，而秩相关系数的抗干扰能力较强。当样本中存在轻微单调非线性畸变或存在严重的单调非线性畸变时，秩相关系数比较合适。

在Pearson 相关系数的基础上，发展了多变量间的相关系数度量：复相关系数(全相关系数)用于衡量一个随机变量Y与多个变量X1,…,Xn之间的相关系数；偏相关系数用于衡量一组随机变量X1,…,Xn中两个变量(Xi,Xj)之间的相关程度；典型相关系数衡量两组变量X1,…,Xn和Y1,…,Ym之间的相关程度，将变量在一定的约束条件下进行线性变换，获得具有代表性的两个综合变量，再根据综合变量之间的相关系数反映两组指标之间的整体相关性。关于两变量组之间的线性关联系数的研究，通常有很多不同的策略。本节主要介绍两种经典的方法。

2.1.1 典型相关系数

历史上第一个变量组间的关联系数是由Hotelling于1936年提出的典型相关分析(Canonical correlation analysis，CCA)中得到的典型相关系数(Canonical correlation coefficient，CCC)[31]。它寻找第一个变量组的线性组合使得与第二个变量组的线性组合关联性最大，由此获得的关联系数称为是典型的，线性组合称为是典型变量。其余的典型变量也可以递归地找到，但是变量与之前找到的典型变量对正交。

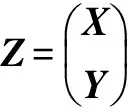
CCA提供了一系列的典型相关系数，因此由典型相关系数刻画的两个变量组之间的关联不是一个全局度量。因为关系的强度是由部分变量组成的。CCA的发展中也有基于全局变量的相关系数但核心依赖于典型相关系数[23]。典型相关系数是带约束的Pearson相关系数，具有Pearson相关系数的性质。将CCA与别的统计方法结合也取得一些很好的效果[32]。

2.1.2 RV系数

若将随机向量X和Y看作两个变量簇，可以通过比较两个点簇间协方差结构的相似性确定两个随机向量间的关联系数。因此，RV系数(RV coefficient)提供了一个变量对间样本关联系数的全局度量[33]。

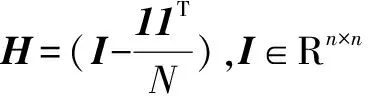
(1)

RV系数的性质：

(1)当p=q=1，时，RV=r2，r2是样本相关系数的平方。

(2)0≤RV≤1，RV=0表明随机向量X和Y之间不相关，X′Y=0；RV=1表面由两个数据集诱导的结构相似。如果Y=XB+1C，其中B是p×q的矩阵，1∈Rn×1是取值为1的向量，C是1×q的常数向量，则RV=1。

2.1.3 最大相关系数

2.2 基于独立性检验的关联关系度量

独立性分析是概率论与统计学中重要的研究内容。比如在假设检验中，构造一个统计度量γ，如果γ(X,Y)=0,则称随机变量X和Y在γ度量下是统计独立。如果γ(X,Y)≠0，称随机变量X和Y在γ度量下是统计不独立的。在实际应用中更感兴趣的是如果两随机变量不独立，它们之间存在什么依赖关系。

2.2.1 基于分布函数的关联度量

由Sklar定理知，存在一个d维连接函数C对所有(x1,x2,…,xd)∈Rd，使得联合分布函数与边际分布函数存在关系：F(x1,x2,…,xd)=C(F1(x1),F2(x2),…,Fd(xd))[35]。在此基础上，Schweizer Wolff等人研究了关于Lp距离的相关系数，分别得到L1,L2,L∞范数的关联度量系数Wolf′sσ，Hoeffding′sΦ2和Wolf′s κ，即

(2)

(3)

(4)

式中：(u,v)∈I2=[0,1]×[0,1]，C(u,v)为I2上的概率分布函数，∏(u,v)=uv为I2上的独立copula函数[36]。

copula函数具有只需研究随机向量X和Y之间的依赖程度而不关心X和Y内部的依赖等一些良好的性质，因此受到广泛关注，Nelsen建立了copula函数与传统相关系数之间的关系[37]，Ding等提出不同维随机向量之间的关联系数，该度量不仅能刻画变量之间的线性关系，还能发现非线性关系，对噪声具有鲁棒性[28]。

2.2.2 基于概率密度函数的关联度量

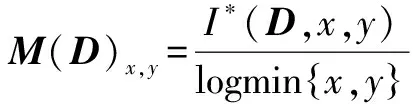
2.2.3 基于特征函数的关联度量

(5)

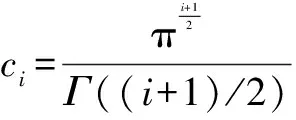
(6)

式中：ν2(X,X)=ν2(X),ν2(X,Y)=ν2(Y)为距离方差。

(2)如果随机向量X和Y是一维标准正态分布，则R2(X,Y)是ρ(X,Y)的非减函数,并且有

(7)

(3)具有线性仿射不变性：对向量X和Y进行如下变换X→a1+b1C1X，Y→a2+b2C2Y，其中a1,a2是任意向量，b1,b2是任意非零实数;C1,C2是任意正交矩阵;则变换后的距离相关系数不变。

(4)由ν2(X,Y)的表达式可知dCor是基于加权L2距离构造的，改变权重函数ω和距离范式Lp都可以得到不同的距离度量公式。

(8)

(9)

对变量间欧式距离进行核变化，给小距离变量对更多的重要性，使得变换后的距离能更好地抓住函数关系的局部性质，相比欧式距离能更好地捕捉各种关联关系。该系数与RV系数的构造思想相同，只是样本矩阵进行了三次中心化处理，最大相似系数的最大值依赖于参数，但是不局限于识别线性关系。

关于关联关系的度量方法还有很多，本文不做赘述，只从经典关联系数的基本构造角度出发进行总结，以期对大数据关联关系新范式的构造提供启发。

3 大数据变量间关联关系度量可能满足的条件

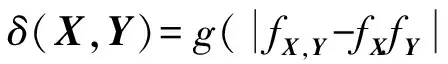
大数据的特征使得变量间关联关系测度比传统相关关系度量的要求更高。面对大数据时代关联关系度量带来的挑战，构造新的能够刻画这些挑战的关联度量势在必行。本文结合文献[28,34,36]给出的度量公理化标准与大数据表现出的特点，试给出大数据关联度量可能需满足的一些性质，δ(X,Y)表示两随机变量之间的关联度量。

(1)δ(X,Y)可以度量任意两个随机变量(向量)X和Y，只要X和Y不处处为常数；要求δ不仅能分别识别连续型和离散型随机变量，还能识别混合型变量形式。

(2)δ(X,Y)=δ(Y,X)。要求δ具有对称性，随机变量X和Y在度量中的位置不影响度量值的大小。

(3)0≤δ(X,Y)≤1。这个实数值仅仅为了比较，它的范围可以是任意的。把范围控制在[0,1]之间也便于不同方法之间的比较，1表示严格的依赖关系，0表示相互独立。

(4)δ(X,Y)=0当且仅当X和Y统计独立。独立一定不相关(线性)，不相关(线性)不一定独立(正态分布除外)。例如随机变量X～N(0,1)，Y=X2,变量X和Y之间有很强的关联关系(二次函数形式)，但是E(X-EX)(Y-EY)=E(XY)-(EX)(EY)=EX3-(EX)(EX2)=0,因为标准正态分布的任何奇数阶矩都是零。因此ρX,Y=0不能说明变量X和Y是独立的,即皮尔逊相关系数ρX,Y不能识别非线性关系，因此要求度量δ具有普适性，能检测到任何关联形式。

(5)δ(X,Y)=1当随机向量X和Y满足X=f(Y)或Y=g(X)，其中f,g是Borel可测函数。所谓Borel可测函数就是Borel集(可测集E[δ>a],∀a∈R称为Borel集)上的实函数，f,g不一定是严格单调连续函数。

(6)如果Borel可测函数f(x),g(y)与Range(x),Range(y)一一映射，则δ(f(X),g(Y))=δ(X,Y)即随机变量经过一些单调或可逆变换，变量间关联强度保持不变，Range(·)是变量的定义域。

(7)如果X和Y的联合分布正态分布，则δ(X,Y)=f(|ρ(X,Y)|)，其中ρ(X,Y)是X和Y的Pearson相关系数。在正态分布情况下，δ是ρ的严格增函数。

(8)若随机变量Y=f(X)+η，Z=g(X)+η，η为噪声项且噪声量相同，则δ(Y,X)=δ(Z,X)。即度量δ不受噪声影响，只与变量的关联强度有关，具有一定的鲁棒性。关联度量的主要目的是用来排序变量对的关联强度得分，因此度量δ与具体关联形式无关。度量δ能够正确地反映隐藏在噪声背后的判别关系(线性或者非线性)强度。

由于大数据中关联关系的多样性、多模态性以及价值密度低等特性，新的度量需具有普适性，对任何关联形式没有偏向。由于数据噪声的影响，希望关联关系能够识别噪声背后真正的关联关系，防止出现伪相关或者忽略了一些重要的变量关联关系，因此一个稳健的关联关系度量在大数据时代十分重要。

4 多模态数据中的关联关系度量展望

多模态是大数据时代数据的显著特点之一，关于多模态数据的研究已引起广泛关注[45-48]。在多模态数据中，每个模态之间的信息互为差异，又互为补充，每个模态之间有一定的关联性，挖掘不同模态之间潜在关系是十分值得研究的问题。现有的多模态数据分析主要采用分治融合的思想，主要有3种融合方式：基于数据融合、基于特征融合和基于决策融合[49]。基于数据的融合是直接在原始数据上处理，信息损失少，将融合后的数据看作同一特征空间的数据，可以采用现有的关联度量方法分析。基于特征的融合是先在每个特征空间下进行数据压缩，再将特征合并到一个大空间中，然后在大的特征空间下进行数据挖掘与分析。基于决策级的融合是最高级的数据融合，先从各传感器中获得特征向量，对此空间下的特征进行决策，然后将各个传感器中的决策进行融合得到最终想要的结果。它们的共同之处在于这些特征分析都基于先验知识，结果的有效性难以推广到先验知识匮乏的前言探索领域。

多模态数据多是非结构性的数据，同一模态中的数据表现出高度非线性性，可以改进现有方法进行研究[50-52]。不同模态间结构关联关系研究鲜有报道，不同模态间潜在的特征关联性度量是大数据关联关系度量的重要问题。传统的方法根据先验事先标注多模态数据之间的关联关系，但是人为标注复杂关联关系几乎不可能。或者在不同模态特征上学习一组权重进行融合，但是变量之间在语义上可能不一致。本文的观点是把不同模态的数据在同一语义空间下进行重新表示。观察一个多模态数据集，变量不在同一个语义空间，很难确定对象的准确空间位置，但是可以学习到每个变量的概率分布，那么是否可以将变量映射到一个概率空间来学习；如果可以学习到每个变量下的邻域或整个特征集上的邻域，是否可以将变量映射到一个邻域空间学习；对象间的差异性不好度量，可以用其他对象作为参照物来刻画，那么是否可以将变量映射到一个由参照物构造的空间中学习。本文尝试利用联合概率解决异构变量造成的挑战，将异构变量组成的属性集转换到同一概率空间下，在新的空间中进行数据挖掘工作并取得良好的效果[53]。同时，如果找到一个度量能够刻画不同模态间的关联关系，但是度量得分高不一定就说明模态间关联关系密切，如何设计统计检验方法检验度量的合理性也是值得注意的问题。

5 结束语

本文从推动大数据挖掘角度出发，结合粒计算的思想，认为关联分析是应对大数据挑战的基础。针对大数据大规模性导致关联关系多样性、多模态性导致异构变量关联关系难刻画、混合性导致噪声量影响关联关系度量的鲁棒性等特点，从构造关联关系度量新范式的角度出发，指出新范式应该具有普适性、均衡性和鲁棒性等特点。大数据关联关系度量的研究还很年轻，尚有诸多问题亟待解决，本文仅对大数据背景下关联关系度量遇到的挑战进行了一些思考，希望能起到抛砖引玉的作用，促进大数据挖掘工作的进展。

[1] Manyika J, Chui M, Brown B, et al. Big data: The next frontier for innovation, competition and productivity[R]. USA, Mckinsey Global Institute, 2011.

[2] 李国杰, 程学旗. 大数据研究:未来科技及经济社会发展的重大战略领域——大数据的研究现状与科学思考[J].中国科学院院刊,2012,27(6): 647-657.

Li Guojie, Chen Xueqi.Big data research：The future of science and technology，economic and social development of major strategic areas： Research status and scientific thinking of big data[J]. Bulletin of Chinese Academy of Sciences, 2012, 27(6): 647-657.

[3] Speed T. A correlation for the 21st century[J]. Science, 2011, 334:1502-1503.

[4] Fan J, Han F, Liu H. Challenges of big data analysis [J]. National Science Review, 2013, 1:293-314.

[5] 李国杰. 大数据研究的科学价值[J].中国计算机学会通讯, 2012, 8(9):8-15.

Li Guojie. Scientific value of big data research[J]. Communications of the CCF, 2012, 8(9):8-15.

[6] 王元卓, 靳小龙, 程学旗. 网络大数据: 现状与展望[J]. 计算机学报, 2013, 35(6): 1125-1138.

Wang Yuanzhuo, Jin Xiaolong, Cheng Xueqi. Network big data: Present and future[J]. Chinese Journal of Computers, 2013, 35(6): 1125-1138.

[7] 孟小峰, 李勇, 祝建华. 社会计算: 大数据时代的机遇与挑战[J]. 计算机研究与发展, 2013, 50(12):2483-2491.

Meng Xiaofeng, Li Yong, Zhu Jianhua. Social computing in the era of big data: Opportunities and challenges[J]. Journal of Computer Research and Development, 2013, 50(12):2483-2491.

[8] Davis J M, Searles Quick V B, Sikela J M. Replicated linear association between DUF1220 copy number and severity of social impairment in autism[J]. Hum Genet, 2015, 134:569-575.

[9] 周志华, 王珏. 机器学习及其应用[M]. 北京:清华大学出版社, 2007.

Zhou Zhihua, Wang Jue. Machine learning and application[M]. Beijing: Tsinghua University Press, 2007.

[10]Reshef D N, Reshef Y A, Hilary K F, et al. Detecting novel associations in large data sets [J]. Science, 2011, 334:1518-1524.

[11]梁吉业,钱宇华,李德玉,等.大数据挖掘的粒计算理论与方法[J].中国科学:信息科学,2015,45(11)：1355-1369.

LiangJiye,QianYuhua,Li Deyu,et al.Theory and method of granular computing for big data mining[J].Scientia Sinica： Informationis,2015,45(11)：1355-1369.

[12]Duran B S, Odell P L. Cluster analysis: A survey [M]. Berlin Heidelgerg： Springer-Verlag, 2013.

[13]Mi Huaiyu, Anushya M, John T C, et al. Large-scale gene function analysis with the panther classification system[J]. Nature Protocols, 2013, 8(8): 1551-1566.

[14]Puth M T, Neuhauser M, Ruxton G D. Effective use of pearson's producte moment correlation coefficient[J]. Animal Behaviour, 2014, 93:183-189.

[15]Puth M T, Neuhauser M, Ruxton G D. Effective use of Spearman's and Kendall's correlation coefficients for association between two measured traits[J]. Animal Behaviour, 2015, 102: 77-84.

[16]孙禄杰, 柏满迎. 相关系数与连接函数[J].统计与决策, 2006(16):4-6.

Sun Lujie, Bai Manying. The correlation coefficient and copula function[J]. Statistics and Decision, 2006(16):4-6.

[17]Alessandro V, Maja P, Dirk H, et al. Bridging the gap between social animal and unsocial machine: A survey of social signal processing[J]. IEEE Transactions on Affective Computing, 2012, 3(1):69-87.

[18]Székely G J, Rizzo M L, Bakirov N K. Measuring and testing independence by correlation of distances[J]. The Annals of Applied Statistics, 2007, 35: 2769-2794.

[19]Székely G J, Rizzo M L. Brownian distance covariance[J].The Annals of Applied Statistics, 2009, 3(4): 1236-1265.

[20]David L P, Philipp H, Bernhard S. The randomized dependence coefficient[C]∥Neural Information Pracessing Systems Foundation. Montreal, Ganada:[s.n.], 2013:1-9.

[21]Gardoso J F. Dependence, correlation and gaussianity in independent component analysis[J]. Journal of Machine Learning Research, 2003, 4:177-1203.

[22]Goodmam L A, Kruskal W H. Measure of association for cross classification,Ⅱ:further discussion and reference[J]. Journal of the American Statistical Association, 1959, 54(285): 123-163.

[23]Bach F R, Jordan M I. Kernel independent component analysis[J]. JMLR, 2002, 3:1-48.

[24]George G, Hass M, Pentland A S. Big data and management[J]. Academy of Manage-ment Journal, 2014, 57( 2) : 321-326．

[25]Christoph B. Autocorrelation type functions for big and dirty data series [EB/OL]. http：∥arXiv.org/pdf/1411.3904v2.pdf,2014-11-14.

[26]张钹. 用人工智能读懂大数据[N]. 中国信息化周报, 2015-06-15.

Zhang Bo. Understanding big data with artificial intelligence [N]. China Information Weekly, 2015-06-15.

[27]Kinney, J B, Atwal G S. Equitability, mutual information, and the maximal information coefficient [J]. Proceedings of the National Academy of Sciences, 2014, 111: 3354-3359.

[28]Ding A A, Yi Li. Copula correlation: An equitable dependence measure and extension of pearson's correlation [EB/OL]. http：∥arXiv.org/pdf/1312.7214v4.pdf,2013-12-27.

[29]Galton F. Co-relations and their measurement, chiefly from anthropometric data [J]. Proceedings of the Royal Society of London, 1888, 45: 135-145.

[30]耿直.大数据时代统计学面临的机遇与挑战[J]. 统计研究, 2014, 31(1):5-9.

Geng Zhi. Opportunities and challenges in the age of big data for statistics [J]. Statistical Research, 2014, 31(1):5-9.

[31]Hotelling H. Relations between two sets of variates [J]. Biometrika, 1936, 28(3/4): 321-377.

[32]卞金洪, 王吉林, 余威风, 等. 基于核主分量分析和典型相关分析的语音情感识别[J]. 数据采集与处理，2014，29(2)：222-226.

Bian Jinhong, Wang Jilin, Yu Weifeng, et al. Speech emotion recognition based on KPCA and CCA[J]. Journal of Data Acquisition and Processing, 2014, 29(2):222-226.

[33]Josse J, Pagès J, Husson F. Testing the significance of the RV coefficient[J]. Computational Statistics and Data Analysis, 2008, 53: 82-91.

[34]Renyi A. On measures of dependence[J]. Acta Mathematica Academiae Scientiarum Hungaricae, 1959, 10:441-451.

[35]Piotr J, Fabrizio D, Wolfgang H, et al. Copula theory and its applications[M]. New York: Springer,2009.

[36]Schweizer B, Wolff E F. On nonparametric measures of dependence for random variables[J]. The Annals of Statistics, 1981, 9: 879-885.

[37]Nelsen R B. An introduction to copulas (Springer series in statistics)[M]. New York, NJ, USA:Springer-Verlag, 2006.

[38]Shannona C E. A mathematical theory of communication[J]. The Bell System Technical Journal, 1984, 27: 379-423, 623-656.

[39]Lejla B, Benedikt G, Emmanuel P, et al. Mutual information analysis: A comprehensive study[J]. J Cryptol, 2011, 24: 269-291.

[40]Moon Y, Rajagopalan B, Lall U. Estimation of mutual information using kernel density estimators[J]. Physical Review E, 1995, 52(3): 2318-2321.

[41]Kraskov A, Stogbauer H, Grassberger P. Estimating mutual information[J]. Physical Review E, 2004, 69(2):1-16.

[42]Joe H. Relative entropy measures of multivariate dependence [J]. Journal of the American Statistical Association,1989, 84: 157-164.

[43]Linfoot E H. An informational measure of correlation [J]. Information and Control, 1957, 1(1):85-89.

[44]Roberto D, Pascual-Marqui D L, Kieko K, et al. A measure of association between vectors based on ＂similarity covariance＂[EB/OL]. http：∥arXiv.org/ftp/arXiv/papers/1301/1301.4291.pdf, 2013-1-18.

[45]Friston K J. Modalities, modes, and models in functional neuroimaging [J]. Science, 2009, 326(5951):399-403.

[46]Zhang Daoqiang, Shen Dinggang. Multi-modal multi-task learning for joint prediction of multiple regression and classification variables in Alzheimer′s disease [J]. NeuroImage, 2012, 59 (2): 895-907.

[47]Zeng Zhihong, Pantic M, Roisman G I, et al. A survey of affect recognition methods: Audio, visual, and spontaneous expressions [J]. IEEE Transactions on Pattern Recognition and Machine Intelligence, 2009, 31(1):39-58.

[48]Guo Z, Zhang Z F, Xing E. Enhanced max margin learning on multimodal data mining in a multimedia database[C]∥Proceeding of 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.[S.l.]：IEEE, 2007, 340-349.

[49]John W f, Willam T, Darrell T, et al. Learning joint statistical models for audio-visual fusion and segregation[C]∥Advance in Neural Information Processing Systems. Danver: MIT Press, 2000, 772-778.

[50]Bucak S, Jin R, Jain A K. Multiple kernel learning for visual object recognition: A review [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014，36(7)：1354-1369.

[51]Yang Meng, Zhang Lei, Zhang David, et al. Relaxed collaborative representation for pattern classification [C]∥Computer Vision and Pattern Recognition(CVPR),2012 IEEE Conference. [S.l.]:IEEE,2012: 2224-2231.

[52]Wu Pengcheng, Hoi Steven C H. Xia Xiao, et al. Online multi-model deep similarity learning with application to image retrieval[C]∥Proceedings of the 21st ACM International Conference on Multimedia (MM2013). [S.l.]:ACM, 2013: 153-162.

[53]Qian Yuhua, Li Feijiang, Liang Jiye, et al. Space structure and clustering of categorical data[J]. IEEE Transactions on Neural Networks and Learning Systems, 2015,99:113.

Review for Variable Association Measures in Big Data

Qian Yuhua1,2， Cheng Honghong1,2， Liang Xinyan1,2， Wang Jianxin1,2

(1.Key Laboratory for Computation Intelligence and Chinese Information Processing of Ministry of Education, Shanxi University， Taiyuan, 030006, China; 2.School of Computer and Information Technology, Shanxi University, Taiyuan, 030006, China)

Association analysis implemented with fantastic association measures is a basis of big data mining, so finding a reasonable measure is a key step for assocization analysis. Firstly, the challenge and research status of association measures are pointed out in the era of big data. From the perspective of the structure of the correlation measure, the exiting measures are systemized, and the properties and applicable corditions are summarized， respectively. Secondly,based on the development of correlation measures and the challanges of big data era, some conditions for meeting association measure are put forward to respond to meetting association measure challeges. Finally， some correlation measures in multi-modal data analysis are discussed and combed, and some ideas are provided to deal with the space conversion from three different angles, which attract more in-depth thinking and research, therefore promoting the progress on big data mining.

big data; association analysis; association measure; multi-modal data

国家优秀青年科学基金(61322211)资助项目;教育部新世纪人才支持计划(NCET-12-1031)资助项目;教育部博士点专项科研基金(20121401110013)资助项目;山西省青年学术带头人基金(20120301)资助项目。

2015-10-10；

2015-11-05

TP181