基于间接认证链的输入测试证明方法
2015-12-26代凯,邓珍荣
基于间接认证链的输入测试证明方法
通信作者: 邓珍荣(1977-),女,广西全州人,副教授,研究方向为网络协议安全、软件架构。E-mail:zhrdeng@ guet.edu.cn
引文格式: 代凯,邓珍荣.基于间接认证链的输入测试证明方法[J].桂林电子科技大学学报,2015,35(1):49-53.
代凯,邓珍荣
(桂林电子科技大学 计算机科学与工程学院,广西 桂林541004)
摘要:针对无法运用认证测试方法中的输入测试对Yahalom协议进行验证的问题,提出一种基于间接认证链的输入测试证明方法。该方法引入间接一致性的概念,解决了Yahalom协议中存在的不完整的挑战-应答机制和输入测试在原证明方法上只具备直接性这2个问题,成功地将输入测试运用于验证Yahalom协议,并将该证明方法推广到对Yahalom-Paulson协议的验证。新的证明方法扩展了输入测试的应用范围。
关键词:安全协议;认证测试;Yahalom协议;间接认证链
收稿日期:2014-03-28
基金项目:广西可信软件重点实验室开放基金(PF13089X)
中图分类号:TP309文献标志码: A
Anewprovingmethodofincomingtestbasedonindirectauthenticationchain
DaiKai,DengZhenrong
(SchoolofComputerScienceandEngineering,GuilinUniversityofElectronicTechnology,Guilin541004,China)
Abstract:Yahalom protocol can’t be verified by incoming test in authentication test, so a new incoming test proving method based on indirect authentication chain is proposed. The concept of indirect consistency is introduced to solve two issues, one is the incomplete challenge-response mechanism in Yahalom protocol, another is directness characteristic in the original proving method of incoming test. This method verifies Yahalom protocol by incoming test successfully, and it is extended to verify the Yahalom-Paulson protocol. The new proving method effectively extends the application range of incoming test.
Keywords:securityprotocol;authenticationtest;Yahalomprotocol;indirectauthenticationchain
随着互联网的飞速发展,网络安全问题变得越来越突出和严峻,解决网络安全问题对于众多网络应用来说是当务之急。安全协议作为网络安全的基础,其安全性对于整个网络的安全起着至关重要的作用,而安全协议工作时复杂的环境条件和判断协议是否能够正常执行的困难性,使得分析安全协议的安全性是一项困难的工作。认证测试方法是一种较新的安全协议分析方法,相较于其他分析方法具有简洁、高效、直观的优点,其更符合安全协议分析领域未来的发展趋势。
认证测试方法[1]是2000年由Guttman等提出的在串空间[2]理论基础上用于判断认证协议一致性的方法,已成功应用于Otway-Rees[3]、Neuman-Stubblebine[4]和NSPK[5]等协议的分析,但现有的文献都没有给出验证Yahalom协议[6]的证明过程。为此,尝试运用认证测试方法对Yahalom协议进行分析。
1Yahalom协议认证性分析
1988年提出的Yahalom协议是一个经典的认证协议,如图1所示。参加协议的主体是通信双方A、B和认证服务器S,其目的是在通信双方之间分配会话密钥。

图1 Yahalom协议 Fig.1 Yahalom protocol
1)A→B:ANa;
2)B→S:B{ANaNb}Kbs;
3)S→A:{BKabNaNb}Kas{AKab}Kbs;
4)A→B:{AKab}Kbs{Nb}Kab。
1.1Yahalom协议的串空间模型
Yahalom协议串空间由以下3类串族组成:
1)发起者串Si,协议迹为:〈+ANa,-{BKabNaNb}KasH,+H{Nb}Kab〉,Si∈Cinit[A,B,Na,Nb,Kab]。
2)响应者串Sr,协议迹为:〈-ANa,+B{ANaNb}Kbs,-{AKab}Kbs{Nb}Kab〉,Sr∈Cresp[A,B,Na,Nb,Kab]。
3)服务器串S,协议迹为:〈-B{ANaNb}Kbs,+{BKabNaNb}Kas{AKab}Kbs〉,S∈Cserv[A,B,Na,Nb,Kab]。
其中H表示主体无法识别的加密信息。假设A,B∈Tname,Kbs∉Kp,Kas∉Kp,Kab∉Tname,Na,Nb∈TTname,Na和Nb在Σ中是唯一起源。Yahalom协议的丛图如图2所示。
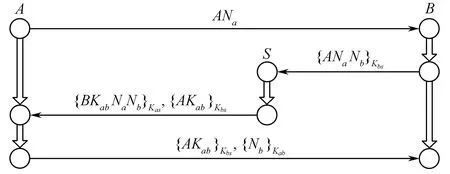
图2 Yahalom协议丛图 Fig.2 The bundle of Yahalom protocol
1.2Yahalom协议的认证性分析
1.2.1服务器S对响应者B的认证
命题1假设C为Yahalom的串空间Σ中的一个丛,A≠B,Kas,Kbs∉Kp,S∈Cserv[A,B,Na,Nb,Kab]的Cheight为1,则C中存在Sr∈Cresp[A,B,Na,Nb,*],其Cheight为2。
证明{ANaNb}Kbs构成主动测试,根据主动测试定理,C中存在正则节点m∈C,t为m的分量,A≠B,{ANaNb}Kbs只能出现在串Sr∈Cresp[A,B,Na,Nb,*]的〈Sr,2〉节点上。命题得证。
1.2.2发起者A对服务器S的认证
命题2 假设Yahalom串空间Σ的丛C中,A≠B,Kas∉Kp,存在串Si∈Cinit[A,B,Na,Nb,Kab],且其Cheight为2,则C中存在S∈Cserv[A,B,Na,Nb,Kab],且其Cheight为2。
证明〈Si,1〉⟹〈Si,2〉构成Na的输入测试,测试分量为{BKabNaNb}Kas,根据输入测试定理,C中应存在Na的正则变换边。根据丛C中的消息类型,该变换边只能在S∈Cserv[A,B,Na,Nb,Kab]上出现。命题得证。
1.2.3 响应者B对发起者A的认证
命题3假设Yahalom串空间Σ的丛C中,A≠B,Kbs∉Kp,存在串Sr∈Cresp[A,B,Na,Nb,Kab],且其Cheight为3,则C中存在Si∈Cinit[A,B,Na,Nb,Kab],且其Cheight为3。
证明〈Sr,2〉⟹〈Sr,3〉构成Nb的输入测试,测试分量为{Nb}Kab,根据输入测试定理,C中应存在Nb的正则变换边。根据丛C中的消息类型,该变换边只能在Si∈Cinit[A,B,Na′,Nb,Kab]上出现,且其Cheight为3。因A与B在参数Na上没有达成直接一致,且没有附加条件能证明Na′=Na。于是,不能证明丛C中存在Si∈Cinit[A,B,Na,Nb,Kab],且其Cheight为3。命题不得证。
2输入测试不能分析Yahalom协议的原因
经过分析发现,输入测试不能验证Yahalom协议的原因有以下2点:Yahalom协议的特殊性和认证测试协议证明方法的局限性。
2.1Yahalom协议的特殊性
Yahalom协议的设计是很微妙的[6],在信息4)中,响应者B收到的不是像Otway-Rees协议一样通信的不同实体只收到一个来自可信第3方(TTP)的证书,而是来自发起者A的2个证书。其中一个证书包含密钥Kab,但未保证新鲜的标识,而另一个证书却用未证实安全的密钥Kab对其加密。后一个证书能否作为证明密钥Kab新鲜性的证据,其依赖于在不完整的挑战-应答过程中被密钥Kab加密的Nb的保密性,之所以称这个挑战-问答过程是不完整的,是因为在信息4)中只有发起者A对响应者B的挑战,而没有响应者B对发起者A的应答。
2.2认证测试协议证明方法的局限性
认证测试方法通过找出信息所在的确切位置证明信息的一致性。Guttman[1]只考虑了直接的认证过程而未考虑通过第3方的认证过程,也就是测试分量多次变换后参数的间接一致性的问题。例如在Yahalom协议中,响应者B对发起者A发起的认证,输入测试〈Sr,2〉⟹〈Sr,3〉就存在这2个对应的变换边〈S,1〉⟹〈S,2〉和〈Si,2〉⟹〈Si,3〉。Guttman直接运用输入测试的证明方法,未考虑通信实体之间间接的认证过程,导致无法采用输入测试对Yahalom进行正面的验证。经分析发现,实体之间的认证关系可通过间接认证实现,即采用一串直接认证的间接认证链证明实体间的认证性。
3间接认证链方法的提出
3.1参数直接一致性和参数间接一致性
协议的认证等级与协议实体在通信中对参数的一致程度有着密切的关系[7],因此,在提出间接认证链方法前,先定义参数直接一致性和参数间接一致性。
定义1参数直接一致性:若在认证测试中直接由测试分量的项就能确定一致的参数,则B对于A在该参数上有直接一致性。
定义2参数间接一致性:若Nb唯一起源于B,且主体B对A在Nb上达成直接一致,而对Na未直接一致,但A对于C在Na和Nb上有直接一致性。若有C=B,则主体B对A在Na达成间接一致;若C≠B,但C对于D在Na和Nb上有直接一致性,若D=B,则主体B对A在Na达成间接一致。
把参数分为主体标识、随机数和协商数据3个种类[8],当主体标识达成直接一致,Na与Nb中只有一个参数直接一致时,若要证明另一个参数一致,则要证明另一个参数满足参数间接一致性。
3.2参数间接一致性的证明方法
假如B对A进行认证,项a唯一起源于B,那么认证的方法就围绕a进行。其步骤为:
1)假设认证方(B)的串执行完毕。
2)求出认证方(B)与被认证方(A)的参数一致的情况,若项a在对话中达成直接一致,而其他项b没有,要证明b在对话中达成间接一致,就要考虑以A为认证方时,被认证方(B或者是可信第3方S)的参数一致的情况,但有个条件,就是B的测试分量对应在A上的变换边或节点的Cheight一定要大于等于以A为认证方时测试分量所在A的Cheight。
3)若步骤2)中认证的S不等于B,则继续步骤2);若S等于B,则比较初始认证方与S的参数一致性情况;若B与S在a上达成一致,则b与b′是相同的。
3.3间接认证链方法
当通信双方无法仅通过彼此的直接证明确定认证等级时,可通过对未认证一致的参数证明其具有参数间接一致性,从而完成对协议认证等级的证明。
4间接认证链方法证明Yahalom协议
4.1发起者A对响应者B的认证
命题4假设Yahalom串空间Σ的丛C中,A≠B,Kas∉Kp,存在串Si∈Cinit[A,B,Na,Nb,Kab],且其Cheight为2,则C中存在Sr∈Cresp[A,B,Na,Nb,*],且其Cheight为2。
证明若Si∈Cinit[A,B,Na,Nb,Kab],且Cheight为2,根据命题2只能证明S∈Cserv[A,B,Na,Nb,Kab],且其Cheight为2。又由命题1,间接证明Sr∈Cresp[A,B,Na,Nb,*],其Cheight为2。命题得证。
4.2响应者B对发起者A的认证
命题5 假设Yahalom串空间Σ的丛C中,A≠B,Kbs∉Kp,存在串Sr∈Cresp[A,B,Na,Nb,Kab],且其Cheight为3,则C中存在Si∈Cinit[A,B,Na,Nb,Kab],且其Cheight为3。
证明〈Sr,2〉⟹〈Sr,3〉构成Nb的输入测试,测试分量为{Nb}Kab,根据输入测试定理,C中应存在Nb的正则变换边。根据丛C的消息类型,该变换边只能在Si∈Cinit[A,B,Na′,Nb,Kab],且其Cheight为3。因A与B在参数Na上未达成直接一致,且Nb在B上是唯一起源,对Si运用命题4,证明丛C中存在Sr′∈Cresp[A,B,Na′,Nb,*],且其Cheight为2。由响应者串的形式,Nb起源于〈Sr′,2〉,因Nb是唯一起源,故〈Sr′,2〉=〈Sr,2〉,因此,Sr′=Sr,Na′=Na。于是,丛C中存在Si∈Cinit[A,B,Na,Nb,Kab],且其Cheight为3。命题得证。
本证明与Guttman[9]使用基于新进性输出测试证明的结论效果相同,且与文献[10]使用理想与诚实证明的结论也相同,从而表明了间接认证链方法的正确性。
5间接认证链方法的应用
5.1Yahalom-Paulson协议
为了证明间接认证链方法具有广泛适用性,将该方法推广到对Yahalom-Paulson协议的分析。Burrows等[11]使用BAN逻辑对Yahalom协议进行分析后指出,在协议运行过程中,若存在恶意的参与者,则存在对协议的重放攻击。Burrows将Yahalom协议改进为BAN-Yahalom协议,并采用BAN逻辑证明了BAN-Yahalom协议的安全性。Syverson[12]给出了对BAN-Yahalom协议的2种攻击,Paulson[6]修改了BAN-Yahalom协议,给出了Yahalom-Paulson协议,如图3所示。
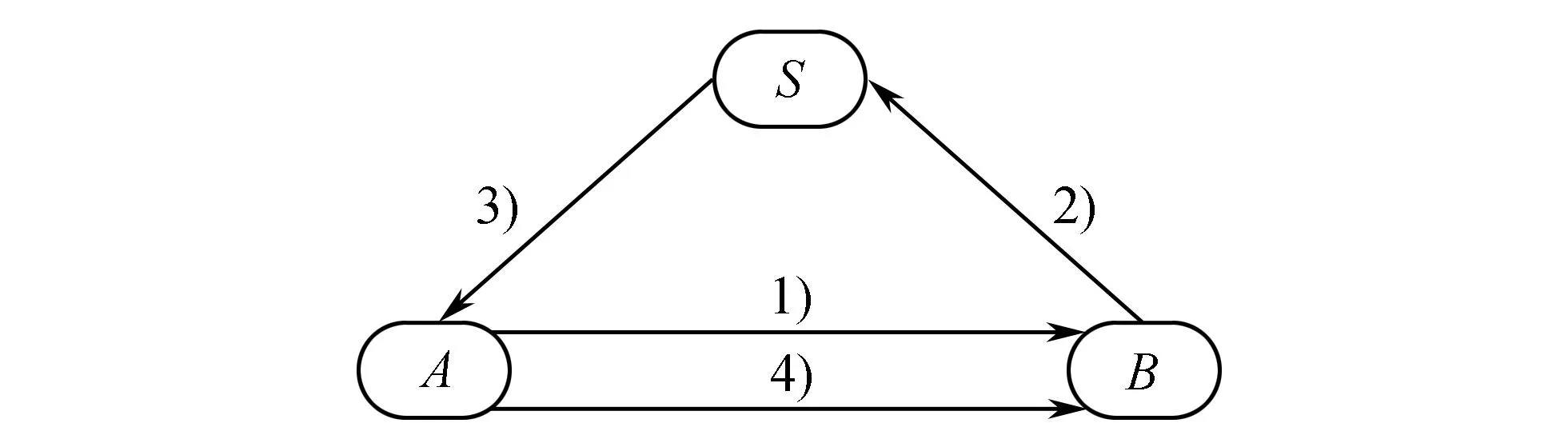
图3 Yahalom-Paulson协议 Fig.3 Yahalom-Paulson protocol
1)A→B:ANa;
2)B→S:BNb{ANa}Kbs;
3)S→A:Nb{BKabNa}Kas{ABKabNb}Kbs;
4)A→B:{ABKabNb}Kbs{Nb}Kab。
Yahalom-Paulson协议串空间由3类串族组成:
1)发起者串Si,协议迹为:〈+ANa,-Nb{BKabNa}KasH,+H{Nb}Kab〉,Si∈Cinit[A,B,Na,Nb,Kab]。
2)响应者串Sr,协议迹为:〈-ANa,+BNb{ANa}Kbs,-{ABKabNb}Kbs{Nb}Kab〉,Sr∈Cresp[A,B,Na,Nb,Kab]。
3)服务器串S,协议迹为:〈-BNb{ANa}Kbs,+Nb{BKabNa}Kas{ABKabNb}Kbs〉,S∈Cserv[A,B,Na,Nb,Kab]。
其中H为主体无法识别的加密信息,假设A,B∈Tname,Kbs∉Kp,Kas∉Kp,Kab∉Tname,Na,Nb∈TTname,Na和Nb在Σ中是唯一起源。Yahalom-Paulson协议的丛图如图4所示。
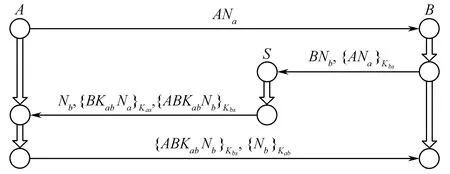
图4 Yahalom-Paulson协议丛图 Fig.4 The bundle of Yahalom-Paulson protocol
5.2Yahalom-Paulson协议的认证性分析
5.2.1服务器S对响应者B的认证
命题6 假设C为Yahalom-Paulson的串空间Σ中的一个丛,A≠B,Kas,Kbs∉Kp,S∈Cserv[A,B,Na,Nb,Kab],且其Cheight为1,则C中存在Sr∈Cresp[A,B,Na,**],其Cheight为2。
证明{ANa}Kbs构成主动测试,根据主动测试定理,C中存在正则节点m∈C,t为m的分量,A≠B,{ANa}Kbs只能出现在串Sr∈Cresp[A,B,Na,**]的〈Sr,2〉节点上。命题得证。
5.2.2发起者A对服务器S的认证
命题7 假设Yahalom-Paulson串空间Σ的丛C中,A≠B,Kas∉Kp,存在串Si∈Cinit[A,B,Na,Nb,Kab],且其Cheight为2,则C中存在S∈Cserv[A,B,Na,*,Kab],且其Cheight为2。
证明〈Si,1〉⟹〈Si,2〉构成Na的输入测试,测试分量为{BKabNa}Kas,根据输入测试定理,C中应存在Na的正则变换边。根据丛C的消息类型,该变换边只能在S∈Cserv[A,B,Na,*,Kab]上出现。命题得证。
5.2.3响应者B对服务器S的认证
命题8 假设Yahalom-Paulson串空间Σ的丛C中,A≠B,Kbs∉Kp,存在串Sr∈Cresp[A,B,Na,Nb,Kab],且其Cheight为3,则C中存在S∈Cserv[A,B,*,Nb,Kab],且其Cheight为2。
证明〈Sr,2〉⟹〈Sr,3〉构成Nb的输入测试,测试分量为{ABKabNb}Kbs,根据输入测试定理,C中应存在Nb的正则变换边。根据丛C的消息类型,该变换边只能在S∈Cserv[A,B,*,Nb,Kab]上出现。命题得证。
5.2.4响应者B对发起者A的认证
命题9 假设Yahalom-Paulson串空间Σ的丛C中,A≠B,Kbs∉Kp,存在串Sr∈Cresp[A,B,Na,Nb,Kab],且其Cheight为3,则C中存在Si∈Cinit[A,B,*,Nb,Kab],且其Cheight为3。
证明〈Sr,2〉⟹〈Sr,3〉构成Nb的输入测试,测试分量为{Nb}Kab,根据输入测试定理,C中应存在Nb的正则变换边。根据丛C的消息类型,该变换边只能在Si∈Cinit[A,B,Na′,Nb,Kab]上出现,且其Cheight为3。因A与B在参数Na上未达成直接一致,且Kab在S上是唯一起源,这里使用参数间接一致性的证明方法,对Si运用命题7,证明丛C中存在S′∈Cserv[A,B,Na′′,Nb′,Kab],且其Cheight为2。由服务器串S的形式,Kab起源于〈S′,2〉,因Kab是唯一起源,故〈S′,2〉=〈S,2〉,因此,S′=S,Na′′=Na′,Nb′=Nb。于是,丛C中存在Si∈Cinit[A,B,Na′,Nb,Kab],且其Cheight为3。命题得证。
6结束语
采用认证测试方法对Yahalom协议进行验证的过程中发现,协议中不完整的挑战-应答机制以及认证测试方法在证明方式上的局限性是导致输入测试不能证明Yahalom协议的原因。采用间接认证链方法,证明了Yahalom协议,并证明了Yahalom-Paulson协议的正确性,新的证明方法扩展了输入测试方法的应用范围。
参考文献:
[1]GuttmanJD,ThayerFJ.Authenticationtestsandthestructureofbundles[J].TheoreticalComputerScence,2002,283(2):333-380.
[2]ThayerFJ,HerzogJC,GuttmanJD.Strandspaces:whyisasecurityprotocolcorrect[C].LosAlamitos:IEEEComputerSocietyPress,1998:160-171.
[3]ThayerFJ,HerzogJC,GuttmanJD.Strandspaces:provingsecurityprotocolscorrect[J].JournalofComputerSecurity,1999,7(23):191-230.
[4]NeumanBC,StubblebineSG.Anoteontheuseoftimestampsasnonces[J].OperatingSystemsReview,1993,27(2):10-14.
[5]卿斯汉.安全协议[M].北京:清华大学出版社,2005:124-127.
[6]PaulsonLC.Relationsbetweensecrets:twoformalanalysesoftheYahalomprotocol[J].JournalofComputerSecurity,2001,9(3):197-216.
[7]杨明,罗军舟.安全协议关联性分析[J].通信学报,2006,27(7):39-45.
[8]杨明,罗军舟.基于认证测试的安全协议分析[J].软件学报,2006,17(1):148-156.
[9]GuttmanJD.Keycompromise,strandspaces,andtheauthenticationtests[C]//Proceedingsofthe7thConferenceontheMathematicalFoundationsofProgrammingSemantics,ElectronicNotesinTheoreticalComputerScience.London:Springer-Verlag,2001:141-161.
[10]丁萌伟,周清雷,赵东明.Yahalom-Paulson协议的串空间模型与分析[J].计算机工程与应用,2008,44(22):97-99.
[11]BurrowsM,AbadiM,NeedhamRM.Alogicofauthentication[J].ProceedingsoftheRoyalSocietyofLondon,1989,426:223-271.
[12]SyversonP.Ataxonomyofreplayattacks[C]//ProceedingsoftheComputerSecurityFoundationsWorkshop,1994:187-191.
编辑:翁史振
