比多比少应用题的解题方法

王洪朋

王洪朋/榆树市新庄中心小学教师（吉林榆树130400）。

比多比少应用题贯穿小学各年级数学课程之中。因此，这类应用题是小学数学教学的重点。解这一类型的应用题，大多数学生总是凭着直觉去做判断，看到多几就用加法，看到少几就用减法。很难抓住关键解决问题。所以，这类应用题又是小学数学教学中的难点。由此看来，分析数量关系明确计算方法，找出解题规律是很有必要的。

一、理解题意，理清数量

例1.同学们自制学具，小红制三角形7个，正方形4个。三角形比正方形多几个？

例2.同学们自制学具，小红制三角形7个，正方形4个。正方形比三角形少几个？

这两个题很简单，用学具亲手摆一摆，比一比，再观察一下就能解答。如下图

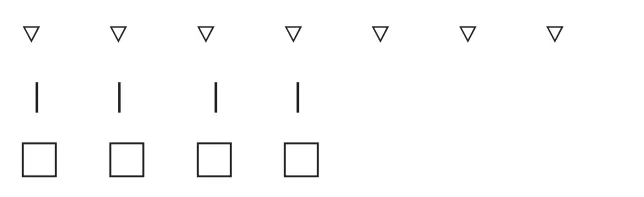
求三角形比正方形多几个，在7个三角形中减去正方形数4，剩下的3个就是三角形比正方形多的个数，也是正方形比三角形少的个数。

做法是：7－4=3（个）

上面两个题，都是已知三角形个数和正方形个数。求正方形和三角形相差的部分“3”个。我们把相差部分的“3”叫做“相差数”。

回过头来，分析题中数量，重点从“比”字句入手，先弄清下面几个问题：

1.题中是谁和谁比？（三角形和正方形比）。

2.谁是较大数？谁是较小数？（三角形是较大数，正方形是较小数）。

3.相差多少?（相差 3）

4.求什么数？ （求相差数）。

通过比较和分析我们可以知道，这类应用题中共有三种数量，分别是：较大数、较小数、相差数。理清了题中数量，再弄清数量之间的关系，找出解题规律。比多比少的应用题就容易解答了。

让学生们在“比字句”中掌握其中的数量关系，准确地分清谁是较大数，谁是较小数，相差数是很不容易的。就学生的知识层面来说，他们只是单一地、局部地学习了这类应用题，没有整体地、理性地分析过这类应用题。由于学生读不懂比字句的含义，他们只能停留在单一的、局部的知识层面，迷迷糊糊地感觉多几就加，少几就减。所以，在教低年级学生学习这类应用题时，要参照新课程的教学理念，做到师生互动，让学生脑、手、口并用，引导学生根据题中已知数用自制的学具摆一摆、比一比。通过这种实践去理解比字句的含义，由比字句掌握其中的数量关系。

二、根据数量关系和解题规律

从例1、例2可以得知求相差数要用较大数减去较小数。即：较大数－较小数=相差数。

例3.同学们自制教学具，小红制三角形7个，比正方形多3个。小红制的正方形有多少个？

例4.同学们自制教学具，小红制三角形7个，正方形比三角形少3个。小红制的正方形有多少个？

解例3时，从“比”字句入手理解题意，通过摆一摆、比一比着重理解谁比正方形多3个，答案是三角形比正方形多3个。是三角形和正方形相比，三角形多，是较大数，正方形少是较小数，相差数是3。例4中的比字句也是说三角形和正方形相比，正方形少，三角形多，三角形是较大数，正方形是较小数，相差数是3。虽然例3、例4的说法不同，但是表达的意思是相同的，要指导学生清楚这一点。这两个题所求的问题是相同的，都是正方形有多少个。也就是求较小数。引导学生动一动，用图形实际摆一摆、比一比可知：

三角形有7个，减去比正方形多的3个，正方形应该

是4个。

做法是：7－3=4（个）

求较小数的解题规律是：较大数－相差数=较小数。

例5.同学们自制教学具，小红制正方形4个，比三角形少3个。小红制的三角形有多少个？

例6.同学们自制教学具，小红制正方形4个，制的三角形比正方形多3个。小红制的三角形有多少个？

用例1到例4的分析方法可以得出，例5、例6是求较大数。

求较大数的解题规律是：

较小数+相差数=较大数

至此，我们已经探索出一套解比多比少应用题的规律。探索规律实际是一个发现事物之间的内在联系、发展思维的过程，可以使学生在自主探索与思考中感受到学习的乐趣，使学生热爱数学。把生活当中的知识应用到生活中去、学以致用。

三、掌握解题规律的适用性

以上通过难度较小的低年级题，总结出解题规律。随着年级的增高，解题的难度也要增加，但上述方法仍然适用。

例7.农民伯伯今天摘了120筐黄瓜，比茄子的2倍还多20筐。农民伯伯今天摘了多少筐茄子？

分析：这个题的比字句是说黄瓜的筐数和茄子筐数的2倍相比较，黄瓜的筐数多，是较大数；茄子筐数的2倍少，是较小数，相差数是20。求的是茄子的筐数，需要先求出茄子筐数的2倍，也就是较小数，然后再除以2就求出了茄子的筐数。

根据：较大数－相差数=较小数，可得：

120－20=100（筐）

100÷2=50（筐）

农民伯伯今天摘了50筐茄子。

需要注意的是：不要把100筐当作是茄子的筐数，100筐是茄子筐数的2倍。

到了高年级，题的难度增加了，互相比较的量不是互比的本体，而是发生了不同的变化。这样确定谁和谁比又要提升到一个新的层面。就例7而言，学生很容易按已有的知识水平进行比较，错误认为是黄瓜和茄子相比，甚至还有的学生分不清谁是较大数、谁是较小数。这时，教师要引导学生采用新的方法：借助画重点词帮助学生准确而深刻地掌握比字句的数量关系。例7的比字句中，“比茄子的2倍还多”是重点词句，把它画出来后，再去理解可知，被比的量是“茄子的2倍”，并不是“茄子”。这样可以清楚地知道题中谁和谁比，是黄瓜的筐数和茄子筐数的2倍相比。还需要

注意的是，题中所求问题不是较小数，但是问题与较小数有着密切的关系，较小数是所求问题的2倍，求出较小数100以后，不要把它当作是所求的问题茄子筐数。而是茄子筐数的2倍，还需要应用倍数关系应用题的解题法求出茄子的筐数50。

例8.某汽车厂今天卖出红色轿车177台，比白色轿车的少三台。今天卖出多少台白色轿车？

这个题的比字句是说红色轿车和白色轿车的相比较，白色轿车的是较大数，红色轿车是较小数，相差数是3。求今天卖出多少台白色轿车，需要先求出白色轿车的，也就是较大数。然后根据分数应用题的意义再除以就可以了。

根据：较小数＋相差数=较大数，可得：

177＋3=180（台）

较大数是180台，也就是白色轿车的。

白色轿车的台数是：180÷=200(台)

今天卖出白色轿车200台。

例9.粮店有大米160袋，面粉是大米的。大米比面粉多多少袋？

分析：从这道题的比字句看，是大米袋数和面粉袋数相比较。大米的袋数是较大数，面粉的袋数是较小数，题中没有直接给出面粉的袋数，需要先求出面粉的袋数。最后求大米比面粉多多少袋，就是求相差数。

先求出面粉袋数:160×=140(袋)

根据：较大数－较小数=相差数，可得：

160－140=20（袋）

大米比面粉多20袋。

在例1到例10的探索中，在学生充分经历、感受、体验、感知的基础上，大脑中生成了丰富的数形表象。借助丰富的感性认识及老师的及时引导点拨，他们很容易就感悟到题的正确解法。探索例10这道抽象概括题是在感性认识积累到一定量后必然的理性飞跃，使学生由动作思维过渡到表象思维，再到抽象思维，从而更好地促进新知识的内化建构，拓展了思维的深度和广度。

综上所述，解比多比少这类应用题，首先理清数量，确定谁是较大数、较小数、相差数。然后正确运用解题规律：

较大数－较小数=相差数

较大数－相差数=较小数

较小数＋相差数=较大数

这样，比多比少的应用题就化难为易，迎刃而解了。