基于Kane方法的火箭抛绳系统飞行动力学模型

顾文彬，陆 鸣，2，刘建青，董勤星，陈江海，王振雄

（1.解放军理工大学 野战工程学院，南京210007；2.武汉军械士官学校，武汉430075）

近年来，受全球极端气候变化和地震活动的影响，世界各国重大自然灾害频发。然而，大量救援工作却因自然灾害导致的道路、桥梁被破坏以及深堑峡谷和江河的阻断，贻误了72h最佳救援时机，造成灾区民众生命和财产的重大损失。因此，研究一种能快速形成空中索道，克服深堑峡谷等障碍，渡送救援物资和人员的技术与装备是国家减灾防灾领域亟待解决的问题。

制导火箭抛绳技术能够在复杂地理与气象条件下和极短时间内，将工作索快速而精确地送达彼岸，形成大跨度救援空中通道，满足应急救援人员和物资的渡送要求。因此，制导火箭抛绳技术与装备研制对提高灾害救援的效率，提升当前国家整体应急救援保障能力具有十分重要的意义。而火箭抛绳系统的飞行动力学理论是该问题研究的难点和关键。

制导火箭抛绳的工作过程是：火箭通过钢丝绳与高强度工作绳一端连接，绳索被整齐地码在储绳箱内；发动机点火后，在火药气体推力作用下，火箭沿滑轨向空中飞出，牵引储绳箱里工作绳飞向瞄准点。参与飞行的绳索为变质量柔性系统，它具有无限自由度，动力学特性非常复杂。目前，国内外对于火箭拖带软绳索飞行的复杂动力学问题的研究较少［1－3］。

本文基于 Kane方法［4］，采用“有限段思想”［5－6］对绳索进行建模，建立了抛绳火箭飞行动力学模型，并对其进行动力学特性分析。通过该项研究，提出较为精确的抛绳火箭飞行的动力学模型，为研究绳子对抛绳火箭飞行的扰动以及抛绳火箭制导控制提供理论模型。

1 火箭抛绳系统动力学飞行建模

1.1 基本假设

假设火箭和绳子在同一平面内运动；火箭简化为一个质量点；参与飞行的绳索均匀离散为n个绳段，从火箭拉起端到刚离开地面端标号依次为1，2，…，n。前n－1段每段长度为li，第n段为变长度变质量绳段；不考虑绳段的轴向伸长和弯曲，每个绳段质量集中在远离火箭的一端，大小等于该段的质量；段与段之间通过铰链连接。在绳索不断被拉出的过程中，当最后一段的长度达到设定条件时，长度不再变化，并拉起一个新的绳段n＋1。

1.2 火箭抛绳系统运动学分析

建立图1所示惯性坐标系，以火箭发射点位置为坐标原点，火箭射向的水平方向为x轴，竖直向上方向为y轴，火箭抛绳系统在Oxy平面内运动。

1.2.1 位置分析

设某时刻火箭的位置为（xR（t）yR（t））T，第i个绳段与y轴的夹角为θi（t），i＝1，2，…，n。选取火箭位置（xR（t），yR（t）），以及每个绳段与y轴的夹角θi（t）为广义坐标，则共有n＋2个广义坐标。每个绳段集中质量点处的位置坐标为

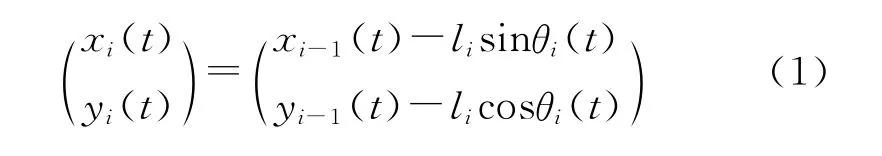
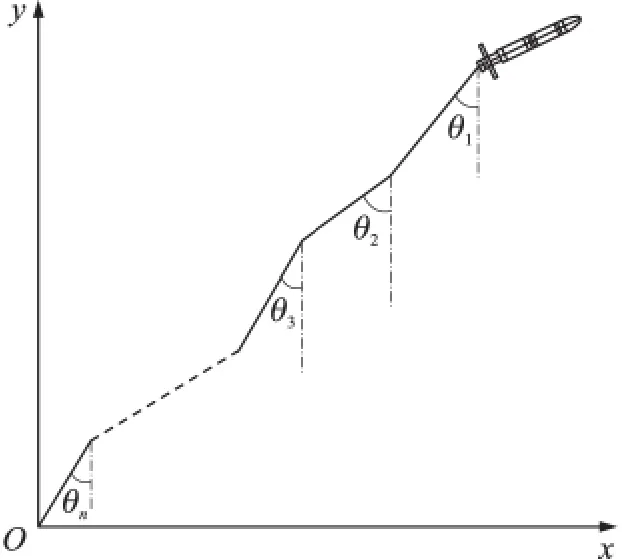
图1 简化模型图

1.2.2 速度分析

对火箭和每段绳段的位置进行求导则得到它们的速度。令（t）＝ωi（t），则火箭速度为（xR（t）yR（t））T，每个绳段集中质量点处的速度为

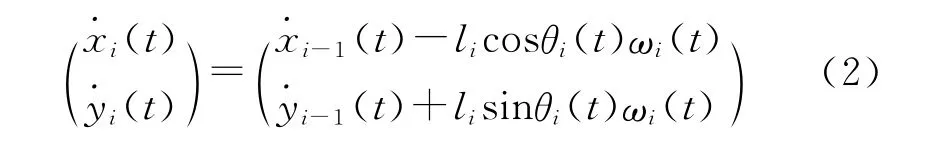
1.2.3 偏速度分析

根据Kane方法推导得各集中质量点相对于各广义速度的偏速度uij表达式：

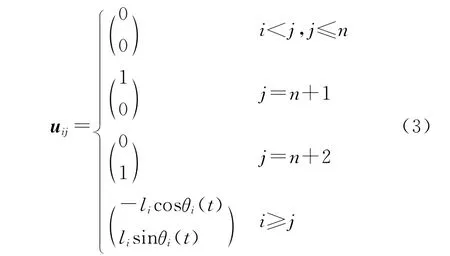
对偏速度求导，得到各偏速度的导数的表达式：

1.2.4 加速度分析

对火箭和每段绳段的速度进行求导可得到它们的加速度，则火箭及每个绳段集中质量点处的加速度为

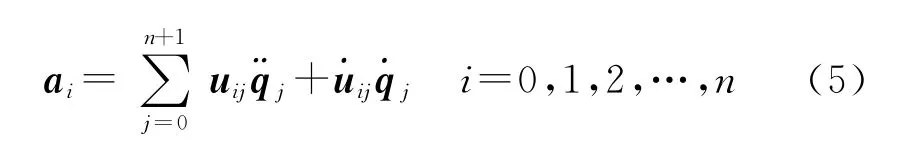
1.3 动力学分析

1.3.1 广义主动力

广义主动力是指作用在火箭拖绳系统上的主动力，由重力Fg、空气动力Fd、推力Fp和末段绳子受力Ft等组成，用FL表示。

1）重力。

火箭的质量为mR，火箭所受重力为

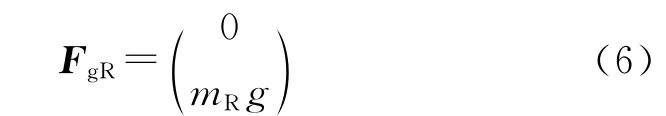
绳子的线密度为ρl，每段绳段的质量为mi＝ρlli，每段绳段所受重力为

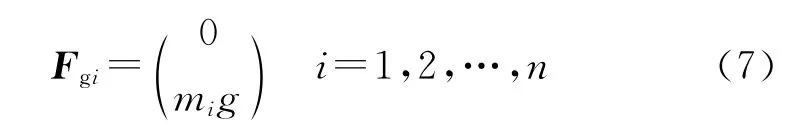
2）空气动力。

火箭在空气中飞行要受到空气动力的作用。实验分析表明：作用在火箭上的空气动力与来流的动压以及火箭的特征面积成正比［7］。假设火箭弹轴与速度矢量重合，则作用于火箭的空气动力沿弹轴向后，空气阻力为

式中：CR为火箭的阻力系数，SR为火箭的特征面积，动压为火箭所处高度的空气密度，vRx、vRy分别为火箭在x轴和y轴方向上的速度。

由于柔软织物具有透气性，所以准确计算绳索所受气动力是非常困难的［8］。考虑到工程需求，采用与火箭所受空气阻力相似的方法，得每段绳段所受空气阻力：

式中：Ci为第i个绳段的阻力系数，Si为第i个绳段的特征面积，qix、qiy为第i个绳段x轴和y轴方向上的动压。

3）推力。

火箭点火后，发动机开始工作，火药气体燃烧，燃烧产物从喷管喷出，从而推动火箭向前飞行。这是推动火箭飞行的动力，该力一直作用在火箭上直到发动机工作结束，称为推力。假设推力沿着火箭弹轴方向，大小为Fp，则：

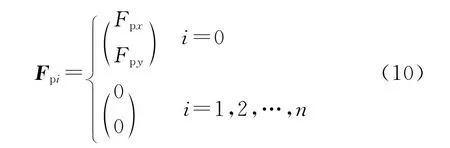
式中：Fpx、Fpy分别为推力沿x轴和y轴的分量。

4）末段绳段所受力。

绳子被不断拉出的过程中，末段绳段的受力相当复杂，根据Wolf的直线拉出模型［9］，假设末段绳段所受力为Ft，则：

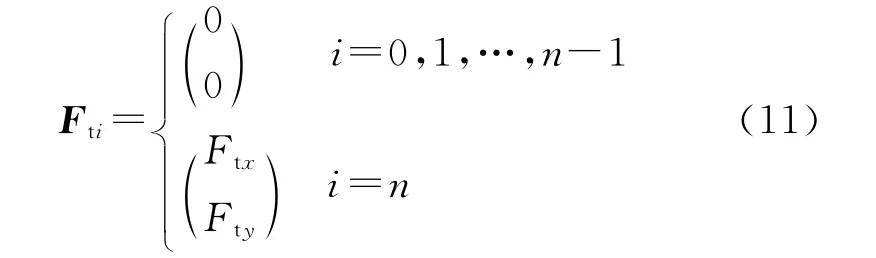
式中：Ftx、Fty分别为末段绳段所受力沿x轴和y轴的分量。

5）主动力合力。

主动力合力用Fz表示，它的表达式为

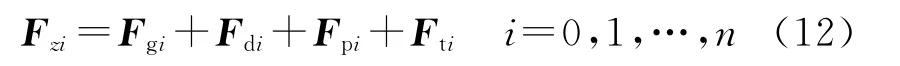
其矩阵形式可表达为

6）广义主动力。

根据Kane法，第j个广义坐标的广义主动力为

整个系统的广义主动力为

1.3.2 广义惯性力

广义惯性力用F＊L表示。根据Kane法，第j个广义坐标的广义惯性力为

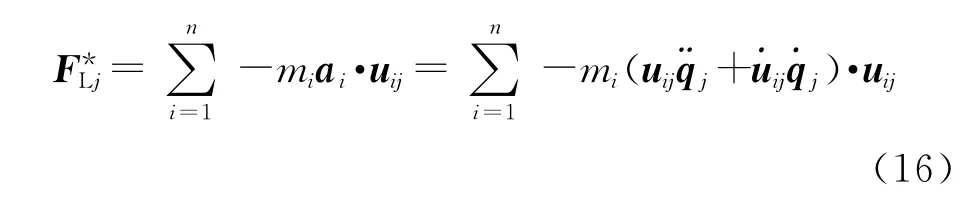
式中：j＝1，2，…，n＋2。

整个系统的广义惯性力为

式中：u、、分 别 为uij、、的 矩 阵 形 式，M＝diag｛m0，m1，…，mn｝。

1.4 动力学方程

根据Kane方程：

将式（17）代入式（18），得：

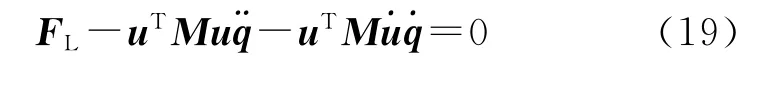
移项得：

式（20）可写为

式中：A＝uTMu，B＝FL－uT

式（21）包含n＋2个方程，共有n＋2个变量，故可解算得火箭及各绳段的运动学参数。

2 仿真计算与讨论

2.1 物理模型

按照所建模型，以某火箭为例进行计算，模型参数：火箭长1m，直径为122mm，质量20kg，火药质量为2.33kg，火箭总冲为4 770N·s，工作时间0.43s，绳索线密度为0.43kg／m，绳索每段取为1m，发射角度分别为25°、35°、45°、55°和65°。

2.2 运动规律

①射角分别为25°、35°、45°、55°和65°时，火箭运动轨迹的变化规律如图2所示。从图2中可以看到：弹道不对称性显著，降弧比升弧陡，顶点距离远大于半射程；随着射角增大，弹道顶点的高度不断增加，而射程先是相应增大，当射角达到某一值后又逐渐减小；在相同条件下，存在一个使抛绳火箭最大射程的射角。

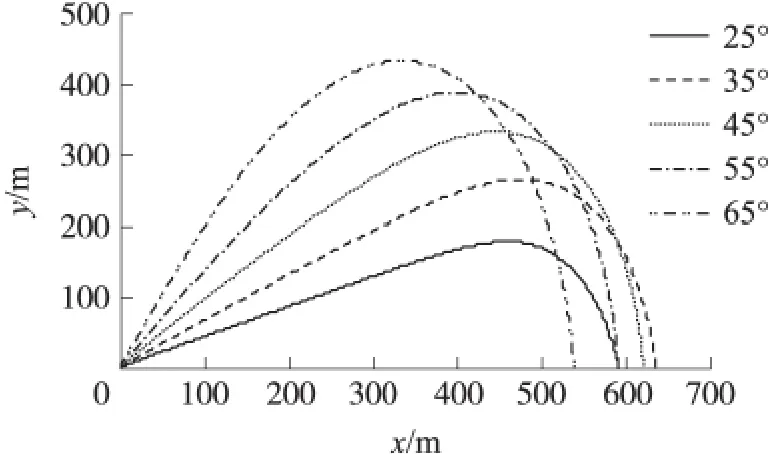
图2 不同射角的弹道轨迹

②火箭速度vR随不同射角的变化规律如图3所示。从图3中可以看到：速度在很短的时间内由0达到最大值，而后开始减小，减小到极小值后又开始增大。主要是在主动段内，火箭发动机工作，火箭发动机推力远比空气阻力、火箭和拉起绳子的重力以及末段绳子所受力大，所以火箭速度快速增加直到达到最大值。主动段结束后，发动机工作结束，此时火箭在惯性作用下仍继续上升，但受到空气阻力、重力以及绳子拉力的作用，速度开始不断减小，直到火箭到达弹道顶点。过顶点后，火箭运动方向改为向下运动，重力加速了这种运动趋势，速度很快降到极小值后又开始增加直到火箭落地；随着射角增大，火箭在空中飞行的时间也增加，火箭的落点速度也相应增加。

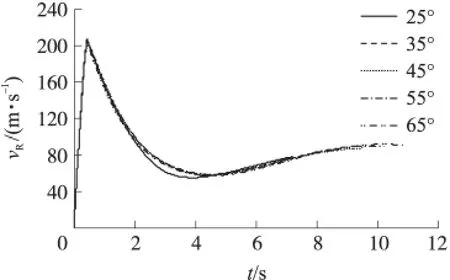
图3 不同射角下火箭速度曲线图

③火箭弹道倾角αR随不同射角的变化规律如图4所示。从图4中可以看到：在初期弹道倾角变化较平缓，随着火箭的飞行，弹道倾角快速减小并由正值变为负值，过零点后继续减小直至落点。主要是在初期，火箭发动机推力起主导作用，弹道倾角变化较缓，发动机工作结束后，重力起主导作用，迫使火箭低头，弹道倾角为0时对应弹道顶点；当射角从25°到65°变化时，火箭落地时的角度都比较大，火箭的降弧比较陡。

图4 不同射角下火箭弹道倾角曲线图

④射角为45°时，抛绳火箭飞行到1.6s、3.7s、5.8s、7.9s时绳子在空中飞行的状态如图5所示。

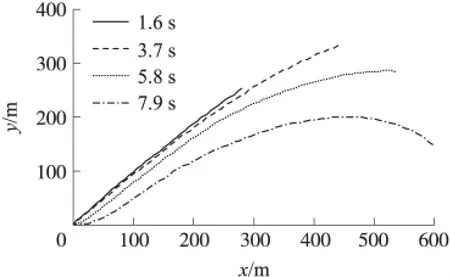
图5 不同时刻绳索的飞行状态图

可以看到：一开始绳子比较平直，到了飞行后期，绳子中间部分出现向上凸的形状。主要是因为飞行初期，火箭发动机推力很大，火箭速度很快，基本在一直线上运动，绳子被快速拉出，因此，绳子较平直；到了飞行后期，火箭速度减小，绳索后端运动滞后于前端，同时由于空气阻力的作用，绳索形成中间部分向上凸的现象，符合实际情况。

⑤射角为45°时，火箭的加速度aR－时间t曲线如图6所示。可以看到：在初始时刻加速度为正值，且值较大，随后开始减小，到0.43s时突变为负值，并继续减小，减小到最小值后开始增大，并越过零点又变为正值，然后曲线变化较平坦。加速度一开始很大是因为此时发动机推力起主要作用。随着速度的增加以及参与飞行的绳子增多，火箭受到空气阻力以及绳子拉力也相应增加，因此，火箭加速度开始减小。加速度发生突变是因为发动机工作结束没有了推力，而空气阻力以及绳子拉力与火箭的运动方向相反。加速度由最小值增大过零点的时刻对应火箭速度最小值的时刻。

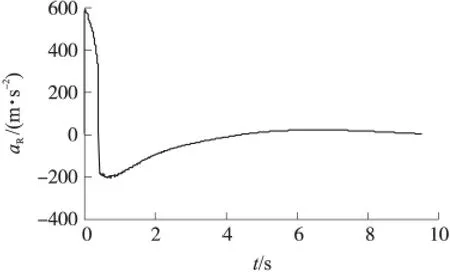
图6 火箭加速度曲线图

3 结束语

对抛绳火箭进行了运动学分析，考虑了作用在火箭和被拉起绳子上的作用力，并将其等效为广义主动力和惯性力，建立了抛绳火箭飞行的动力学模型。

对抛绳火箭进行了数值计算。计算结果表明，该动力学模型能够有效地实现抛绳火箭的数值仿真，揭示运动规律，是一种切实可行的理论模型。

该动力学模型的建立对下一步研究抛绳火箭飞行的扰动以及抛绳火箭的制导、飞行控制具有理论指导意义。

［1］吴小平，郑友祥，丘光申.拖缆火箭弹道计算研究［J］.弹道学报，1995，7（1）：41－49.WU Xiao－ping，ZHENG You－xiang，QIU Guang－shen.Study on ballistics calculation of line throwing rocket［J］.Journal of Ballistics，1995，7（1）：41－49.（in Chinese）

［2］吴宏，李开明.直列装药火箭爆破器爆炸带空气阻力特性研究［J］.工兵装备研究，2003，22（6）：42－44.WU Hong，LI Kai－ming.Study on the air resistance characteristics in explosive hose of rocket－propelled line charge demolition device［J］.Engineer Equipment Research，2003，22（6）：42－44.（in Chinese）

［3］吴宏，王勇.柔性体的有限质点模型弹道计算研究［J］.弹箭与制导学报，2006，26（3）：162－165.WU Hong，WANG Yong.Study of ballistic calculation in finite particles model of flexible body［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2006，26（3）：162－165.（in Chinese）

［4］休斯顿，刘又午.多体系统动力学［M］.天津：天津大学出版社，1987.HUSTON R L，LIU Y W.Dynamics of multibody systems［M］.Tianjin：Tianjin University Publishing House，1987.（in Chinese）

［5］HUSTON R L，KAMMAN J W.Validation of finite segment cable models［J］.Computers and Structures，1982，15（6）：653－660.

［6］WANG Y，HUSTON R L.A lumped parameter method in the nonlinear analysis of flexible multibody systems［J］.Computers and Structures.1994，50（3）：421－432.

［7］韩子鹏.弹箭外弹道学［M］.北京：北京理工大学出版社，2008.HAN Zi－peng.Ballistics of projectile and rocket［M］.Beijing：Beijing Institute of Technology Press，2008.（in Chinese）

［8］MCVEY D F，WOLF D F.Analysis of deployment and inflation of large parachute［J］.Journal of Aircraft，1974，11（2）：96－103.

［9］WOLF D.Dynamics stability of a nonrigid parachute and payload system［J］.Journal of Aircraft，1971，8（8）：603－609.