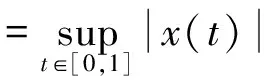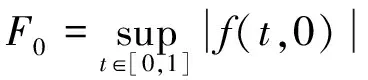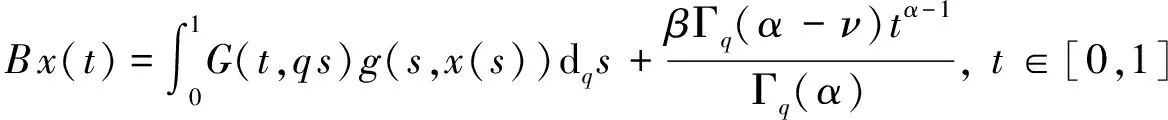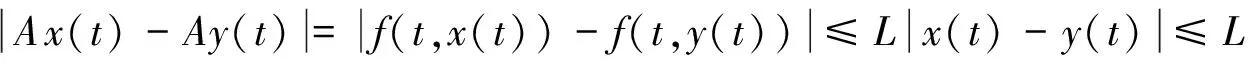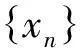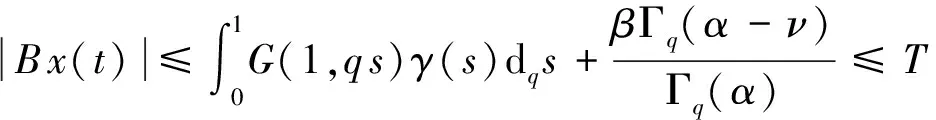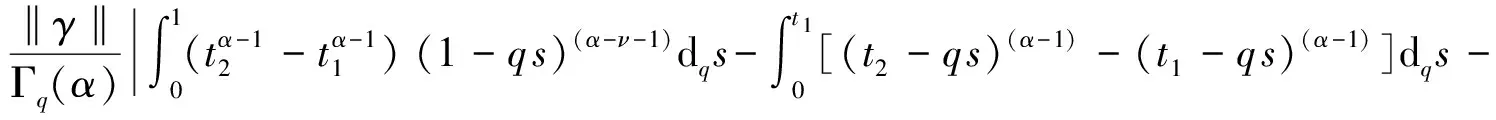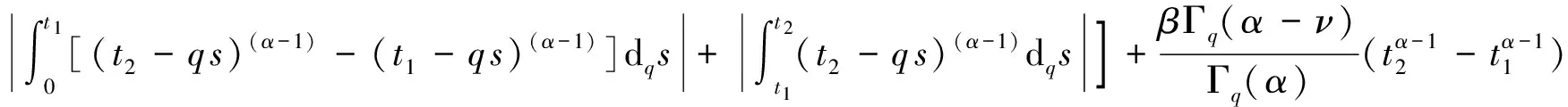一类混合分数阶q-差分边值问题解的存在性
2015-12-26杨潇白俊杰葛琦
杨潇, 白俊杰, 葛琦
( 延边大学理学院 数学系, 吉林 延吉 133002 )
一类混合分数阶q-差分边值问题解的存在性
杨潇, 白俊杰, 葛琦*
( 延边大学理学院 数学系, 吉林 延吉 133002 )
研究了一类带有分数阶q-差分边值条件的混合分数阶q-差分方程解的存在性.首先分析了格林函数的性质,然后借助Lipschitz条件,在Banach代数中利用不动点定理研究了该方程解的存在性,最后通过实例验证了所得结论的合理性.
混合分数阶q-差分; 不动点定理; 解的存在性
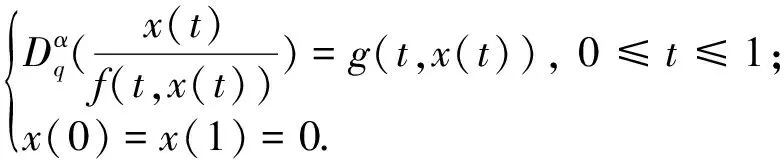
(1)
其中2<α≤3, 0 定义2[6]函数f(x)在区间[0,b]上的q-积分定义为: 定义3[6]Riemann-Liouville型分数阶q-积分定义为: Riemann-Liouville型分数阶q-导数定义为: 引理1[6]设α>0, p是正整数,则 引理2[6]设α,β≥0, f(x)是定义在[0,1]上的函数,则 引理4[6]若α>0, a≤b≤t, 则(t-a)(α)≥(t-b)(α). 引理5[8]设S是Banach代数X上的一个非空的、有界闭凸子集,设A∶X→X和B∶S→X是两个算子,且满足: (i) A满足Lipschitz条件,其中L为Lipschitz常数; (ii) B是完全连续的; (iii) 对于∀y∈S, 有x=A xBy x∈S; (iv) L M<1, 其中M=‖B(S)‖=sup{‖B(x)‖:x∈S}. 则算子方程A xB x=x在S中有一个解. 定理1 设h∶[0,1]→[0,+∞)是连续的,且2<α<3, 1<ν<2, 边值问题 (2) 于是有 引理6[6]Green函数G(t,q s)具有以下性质: (i) G(t,q s)≥0, t,s∈[0,1]; 证明 设X=C([0,1],R), 定义X的子集W={x∈X:‖x‖≤N}, 其中 显然W是X上的一个有界闭凸子集.由定理1知,边值问题(1)与如下方程等价: (3) 定义两个算子A∶X→X和B∶W→X: A x(t)=f(t,x(t)), t∈[0,1], 首先A是X上的Lipschitz算子,其中L是Lipschitz常数.事实上,设∀x,y∈X, 由条件(H1)有 因此,对于∀x,y∈X, 有‖A x-Ay‖≤L‖x-y‖. 即B是W上的连续算子.其次证明B是W上的紧算子,即B(W)是一致有界的,且在X上是等度连续的.事实上,设x∈W, 由引理6和条件(H2)知,对于∀t∈[0,1]有 下面证明引理5中的条件(iii)成立.事实上,设x∈X满足x=A xBy (∀y∈W), 由条件(H1)有 综合以上结果可知,引理5中的条件均被满足,于是算子方程A xBx=x在W中有一个解,即边值问题(1)在W中存在一个解. 注1 当f(t,x)=1时,由文献[6]可知边值问题(1)的解存在. 例1 考虑混合分数阶q-差分边值问题 (4) [1] Ferreira R A C. Nontrivial solutions for fractionalq-difference boundary value problems[J]. Theory of Differential Equations, 2010,70:1-10. [2] Ferreira R A C. Positive solutions for a class of boundary value problems with fractionalq-differences[J]. Computers and Mathematics with Applications, 2011,61(2):367-373. [3] Ricardo Almeida, Natália Martins. Existence results for fractionalq-difference equations of orderα∈]2,3[ with three-point boundary conditions[J]. Communications in Nonlinear Science and Numerical Simulation, 2014,19(6):1675-1685. [4] Zhao Yulin, Chen Haibo, Zhang Qiming. Existence results for fractionalq-difference equations with nonlocalq-integral boundary conditions[J]. Advances in Difference Equations, 2013,2013:1-15. [5] Zhao Yulin, Ye Guobing, Chen Haibo. Multiple positive solutions of a singular semipositione integral boundary value problem for fractionalq-derivatives equation[J]. Abstract and Applied Analysis, 2013,2013:1-12. [6] 孙明哲,韩筱爽.一类分数阶q-差分边值问题的正解[J].延边大学学报:自然科学版,2013,39(4):252-255. [7] Bashir Ahmad, Sotiris K Ntouyas. Fractionalq-difference hybrid equations and inclusions with Dirichlet boundary conditions[J]. Advances in Difference Equations, 2014,2014:1-14. [8] Sun Shurong, Zhao Yige, Han Zhenlai. The existence of solutions for boundary value problems of fractional hybrid differential equations[J]. Communications in Nonlinear Science and Numerical Simulation, 2012,17(12):4961-4967. Existence of solutions for a class of boundary value problems with hybrid fractional q-differences YANG Xiao, BAI Junjie, GE Qi* (DepartmentofMathematics,CollegeofScience,YanbianUniversity,Yanji133002,China) We study the existence of solutions for a class of the fractional q-differences hybrid equation with the fractionalq-differences boundary conditions. Firstly, some characteristics of the Green function were analyzed. The second, we obtained sufficient conditions for the existence of positive solutions to this equation under Lipschitz condition using fixed point theorems in Banach algebra. The end, the main results were illustrated with the aid of examples. hybrid fractionalq-differences; fixed point theorem; existence of solutions 2014-11-16 *通信作者: 葛琦(1975—),女,副教授,研究方向为常微分方程理论及其应用. 国家自然科学基金资助项目(11161049);吉林省教育厅“十二五”科学技术研究项目(2015—2016) 1004-4353(2015)01-0021-04 O175.6 A1 预备知识
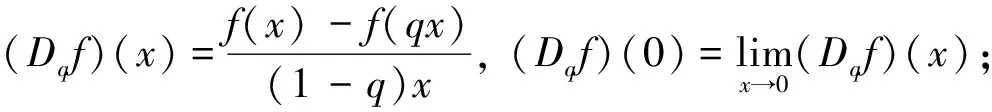

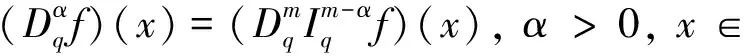


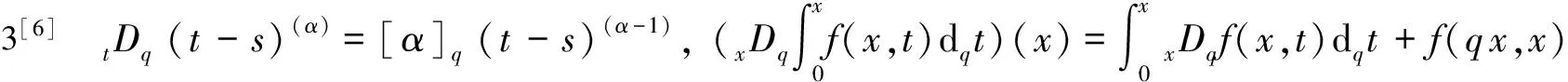
2 Green函数的性质

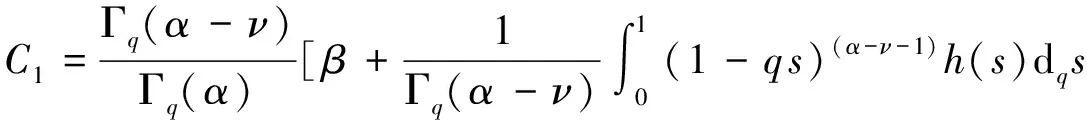
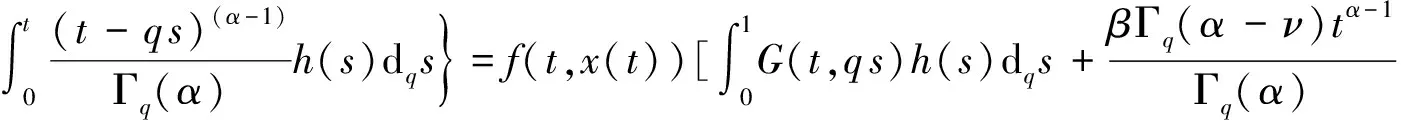
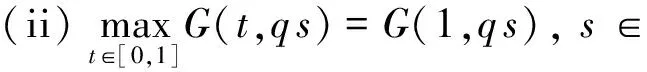
3 解的存在性