A股市场统计套利风险实证分析
2015-12-26赵胜民闫红蕾
赵胜民,闫红蕾
南开大学 金融学院,天津 300071
A股市场统计套利风险实证分析
赵胜民,闫红蕾
南开大学 金融学院,天津 300071
基于转移模型,收集中国A股市场开展融资融券业务的900只股票和15只ETF的数据,采用logt检验和俱乐部收敛检验研究A股市场属于同一行业的融资融券标的股票价格以及融资融券标的ETF价格之间的收敛关系及其动态变化,分析A股市场统计套利的风险,研究发现基于股票所属行业构建套利组合具有较大风险,融资融券的双向交易机制尚未充分发挥,市场有效程度不足,但统计套利在中国市场仍具有可行性。实证结果表明,从整个行业看,融资融券标的股票之间不存在持续、稳定的收敛关系,但同一行业内某些个股之间存在不稳定的俱乐部收敛关系;融资融券标的分阶段扩容增加统计套利的风险,也增加统计套利的机会,扩容之后绝大部分行业个股整体收敛关系消失,但俱乐部数量增加,俱乐部收敛检验可以为选择套利资产组合提供依据;考虑新增标的在内,ETF整体在样本期间内具有稳定的收敛关系,更适合作为套利资产组合。样本外检验证实了前述结果。研究结论为对冲基金进行统计套利风险分析提供经验证据,并为选择套利资产组合提供方法。
统计套利;融资融券;转移模型;logt检验;俱乐部收敛
1 引言
中国融资融券业务发展迅速,转融通业务推进以及标的证券扩容完善了双向交易机制,为投资者提供更多的交易策略和盈利方式,业界不断开发基于融资融券双向交易机制的数量化交易策略。统计套利是目前广泛应用的策略,理论上统计套利是一种自融资、无风险的套利交易,但是从实际经验看,统计套利承担较大风险。
套利既是对有效市场的违背又能促进有效市场的实现,套利的风险和收益一定程度上能够反映市场的有效性[1-3]。统计套利是一种均值回复套利,价差的波动率决定统计套利的风险,同时作为保证金交易,投资者要为潜在的损失提供担保并支付融资利息,价格收敛的速度和幅度决定了套利的成本和收益。套利资产组合价格收敛是套利策略的关键,实践中价差往往呈现一定分布的随机波动,厚尾现象导致套利风险。国外研究从投资者有限理性、套利受限等角度探讨资产价格不收敛的原因以解释统计套利风险,而中国的研究忽略了对价格收敛这个根本前提的分析和检验。已有研究套利策略的构建包括协整分析和Copula方法等[4],然而协整分析在研究金融时间序列的收敛关系上具有较大局限性。本研究系统检验自融资融券业务开展以来全部标的资产价格的收敛性,分析统计套利的风险并提出构建套利组合的方法。
2 相关研究评述
从统计套利的理论定义看,统计套利是一种自融资、无风险、基于波动率收敛的预期收益非负的套利交易[5]。Jarrow等[3]修正了统计套利的定义,认为统计套利并不保证盈利,但是随着时间推移,发生损失的概率越来越小,最终收敛于零,交易策略的方差不能随着时间的延长而无限增长,价差的波动有上限。然而从各国金融市场实际交易数据看,统计套利策略并非无风险,资产组合的价差经常发散并且在极端情况下剧烈波动,使投资者遭受巨大损失。大量研究从不同角度分析价差长期不收敛的原因,以解释统计套利的风险。
套利受限导致交易不足,资产价格无法回归合理价值,价格无法收敛是导致策略风险的重要原因。首先,交易成本妨碍统计套利[6-8],较高的交易成本侵蚀套利利润,阻碍套利者发掘套利机会。其次,制度设计也是影响套利交易的重要因素,包括杠杆限制和保证金合约设计。①作为保证金交易,套利交易是否充分受担保品价值的影响[9]。经济的不利冲击降低担保品的价值,抑制套利交易。同时保证金与资产价格的波动密切相关,不利的冲击之后保证金水平提高,投资者可用资金减少,妨碍套利交易。②对杠杆比例的规定也影响套利的充分性。杠杆约束阻碍套利者纠正错误定价和向市场提供流动性[10],杠杆约束既扩大风险又造成风险传染,随着套利者头寸的变动,一种资产的冲击会传染给另一无关资产,造成定价无效[11]。③保证金比例的要求也影响套利交易,其他条件相同的情况下具有较低保证金比例要求的资产的交易价格更高[12]。④套利资金的可得性也是影响套利交易的重要因素。市场大幅下跌时担保品价值下降导致后续交易不足[13]。以上因素限制了投资者套利交易,从而在套利受限时资产价格无法回归合理价值,价格不收敛。
此外一些学者通过一般均衡模型证明价差本身即是非稳定的,也即统计套利的风险来源于交易本身[14-15],主要归因于投资者资产组合规模限制和套利者能力有限。不利冲击导致价差发散,造成套利者被迫了结部分头寸,进而导致价格继续向不利方向波动和进一步平仓,使价格进一步发散造成套利交易者的巨大损失[16-17]。这些研究的共同特点是假设存在不可预见的外部冲击,而Kondor[18]的一般均衡模型分析套利交易对资产价格的影响,认为即使不存在外部冲击,统计套利交易本身也会造成价格的差异,某些情况下损失巨大。以上研究主要采用理论分析证明套利的局限性和套利损失的可能性,从实证角度分析价格非收敛性特征的研究尚不多见。
统计套利策略的构建主要依据协整理论[19],基于协整分析构建套利组合具有一定的优越性[20]。中国由于交易机制不完善,做空机制引入较晚,对统计套利的研究主要集中于套利策略的构建和检验,研究方法主要是协整检验,研究对象主要是股指期货和ETF,还包括股指期货的跨期套利[21-22]以及股指期货与ETF之间的统计套利[23]。此外,统计套利策略也应用于对基金的研究中,包括对封闭式基金[24]和开放式基金[25]的统计套利以及分级基金A端和B端[26]的统计套利。上述研究中套利资产选择的方法主要是协整检验,但是协整方法在进行价差收敛检验,尤其是波动率较大的股票资产的套利关系检验时存在不足。①协整检验主要是半参数分析,主要应用于较长时间范围的分析,需要较大的样本量,而不适于研究短期波动,时间序列的长度有限时,协整分析并不适用,而统计套利往往基于高频交易数据,对价格波动敏感性较高。②标的资产价格作为微观面板数据收敛速度往往比较缓慢,或者两种金融资产存在渐进协整关系,残差是一个非平稳过程且波动率较大,这种情况下协整检验功效较低。③上述研究主要是基于特定时间范围的研究,而对期间资产价格的动态变化考虑不足,因而一定程度上忽略了模型的风险。④协整检验主要针对有限变量,而统计套利组合资产组合选择较为多样,且资产组合的构造是动态的。综上,协整检验应用于统计套利的研究具有较大局限性。
中国融资融券业务起步较晚但发展较快,做空机制有助于纠正高估的股价[27],减少标的证券暴跌的概率[28],降低标的证券特质性波动[29],提高标的股票的定价效率[30]。许多学者基于融资融券业务设计统计套利策略,包括通过聚类分析和协整分析[31]、行业及相关性分析[32]和基于公司财务指标[33]建立量化的股票筛选模型。上述研究不足之处在于样本量有限,选股指标的具有较强的主观性,缺乏稳健性分析,模型的说服力有限。
综上,中国的研究主要集中于股指期货、ETF和基金等不同金融工具之间统计套利策略的设计,而鲜有研究全面探讨融资融券标的股票统计套利的风险问题。本研究基于Phillips等[34]构建的转移模型动态的研究融资融券标的价格的收敛性,分析统计套利策略的风险,并提出资产组合选择的方法。
3 模型设计
套利定价理论假设投资者是风险规避的,期望效用函数单调递减且具有投资者同质预期,在均衡状态下资产的收益率表示为
ri=E(ri)+βi,1F1+βi,2F2+…+βi,mFm+…+
βi,MFM+εii=1,2,…,N
(1)
E(εi)=E(εiFm)=0
(2)
其中,ri为资产i的随机收益率;Fm为系统风险,m=1,2,…,M,M为系统因子的总数;N为资产总数;βi,m为因子载荷,即资产i的系统风险m的价格;εi为收益率的个体风险,本质上看它是对所有与资产不相关信息的反映,对每一种资产而言都是唯一的,套利定价理论认为影响资产收益率的因子是随机的并在很大程度上是非预期的,只有系统风险才能得到回报,而个体风险可以通过套利交易对冲掉。后续研究放松了原假设关于个体风险εi的独立性的要求,证明资产的个体风险存在相关关系时套利定价理论仍然成立[35],在市场均衡时,个体风险可以通过套利对冲从而不存在套利机会。Roll等[36]采用1962年7月至1972年12月纽约证券交易所(NYSE)和美国证券交易所(AMEX)上市的1 260只股票的收益率数据对套利定价理论进行检验,首先将这1 260只股票按字母顺序进行分组,每组包括30只股票,运行以下步骤。
步骤1 收集一组股票的日回报率数据,并根据每只股票的回报率计算出该组股票的方差和协方差矩阵。
步骤2 运用极大似然因子分析法,确定影响收益率变化的因子个数和因子载荷βi,m。
步骤3 用估计出的βi,m解释不同股票期望收益率在横截面上的差异,估计出每个因子相应的风险溢价及其显著性。
步骤4 每一组股票重复以上3个步骤。
本研究借鉴该方法对A股市场融资融券标的进行处理,按照行业对标的股票进行划分,每个行业提取出1个代表该行业系统风险的因子,并确定因子载荷。
如果将套利定价理论扩展到连续时间序列上,若系统风险唯一,则
ri,t=βi,tFt+εi,tt=1,2,…,T
(3)
其中,ri,t为资产i收益率的时间序列,t为时间,βi,t为时刻t的因子载荷,Ft为时刻t的系统风险,εi,t为资产i随时间变化的风险,T为观测期的总数。在βi,t中加入随机成分,使其成为一个时变的因子载荷δi,t,并吸收εi,t,套利定价模型可以改写为允许个体风险随时间变化、适用于研究不同个体行为的形式,即
ri,t=βi,tFt+εi,t
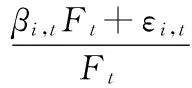
(4)
那么,两种具有相同特征(即相同系统风险)的资产i与资产j之间的价差gi,j可以表示为
gi,j,t=ri,t-rj,t=δi,tFt-δj,tFt=(δi,t-δj,t)Ft
(5)
i≠j
Ft作为系统风险,常常与宏观经济运行和行业发展有关,在短时间内不会出现剧烈变化且不为零,gi,j,t的变动取决于两种资产之间的因子载荷的变动关系。如果δi,t和δj,t这两个序列具有收敛关系,那么ri与rj之间具有收敛关系,gi,j,t趋近于零。所以研究资产i和资产j(i≠j)的价格收敛性等同于研究二者的因子载荷gi,t与gj,t的收敛性。
4 研究方法和数据
4.1 转移模型及收敛检验
研究收敛性问题主要集中在宏观经济变量,如经济增长、地区收入、价格水平、工资水平等问题,使用的方法主要有协整检验、面板单位根检验、最小LM检验等方法,然而这些检验方法不适用于金融面板数据。一方面,当数据的收敛速度较慢、观测值数据量有限时协整检验的功效大大降低;另一方面,如果个体的收敛路径不同,协整检验失效,而实际上统计套利并不要求资产价格具有相同的路径,只要求有限时间内两个资产价格能够收敛。本研究参照Phillips等[34]的转移模型,采用logt回归检验方法进行检验。该检验方法被广泛运用到收敛检验实证分析中,Apergis等[37]用该方法检验股票市场的收敛性,Perlin等[38]用该方法检验欧洲债券市场的套利机会的决定因素。
建立一个半参数模型,即
δi,t=δi+σiξi,tL(t)-1t-α
(6)
其中,δi为因子载荷δi,t的稳定值;σi为δi,t的方差;ξi,t为i.i.d.(0, 1)与时间t变化弱相关的随机波动项;L(t)为关于t的缓变函数,L(t)=logt,随着t→∞,L(t)→∞。σiξi,tL(t)-1t-α模拟了δi,t运动过程的波动过程和对稳定值的偏离程度,α为δi,t偏离其稳定值δi的时间长度,衡量是否收敛及收敛的速度。对于任意α≥0,δi,t最终将收敛于δi,该命题作为具有重要意义的原假设,如果该假设成立,对于∀i≠j,δi=δj,模型可以涵盖δi,t≠δj,t这样的过渡期,因此转移模型涵盖更多可能的转移特征甚至允许发散的情况。
该检验方法具有如下优点。①金融时间序列往往非平稳,而且具有异方差特点,转移模型的假设检验不要求ri,t或Ft满足任何特定的条件,如趋势平稳或随机非平稳等条件。②转移模型作为非线性模型,具有很好的一般性,可以包含δi,t随时间变化的多种路径和波动特性。③转移模型具有良好的实用性,不依赖于数据量。即便是观测值数量有限,也不会影响估计的无偏性。
Ft作为公因子,可以通过如下方法消除其影响,定义相对转移参数为
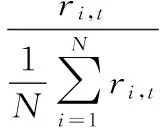
(7)
其中,hi,t为某一时刻资产i的因子载荷占所有资产因子载荷均值的比重。由(7)式可知hi,t具有以下特点,从截面看,某一时点上hi,t的均值为1;如果δi,t收敛于δi,那么hi,t将收敛于1。即在长期,hi,t在时刻t的截面方差将收敛于0,则
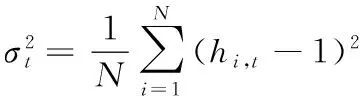
(8)
如果δi和δj在一定时间内都趋于一个稳定值δ,那么资产i和资产j价格收敛,该检验方法称为logt检验,检验的原假设为
H0:δi=δ且α≥0
与此相反,备择假设为
HA:δi≠δ或α<0
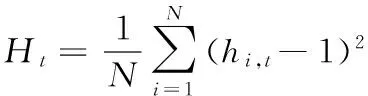
(9)
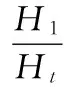
对(10)式进行回归,即
(10)
t=[qT],[qT+1],…,Tq>0
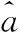
4.2 俱乐部收敛
行业整体收敛的原假设意味着在同一行业内任意若干股票价格之间收敛,但拒绝原假设并不意味行业内所有股票之间全部发散,可能有部分股票在一段时间内存在收敛关系,即总体观测值不收敛,但部分个股之间存在收敛关系。本研究将具有收敛关系的股票集合定义为俱乐部。通过检验俱乐部收敛关系,可以发现这些具有组内收敛关系的俱乐部作为统计套利的机会。
俱乐部检验的基本思想是在个体数量为N、时间长度为T的面板数据中,假设存在一个由k个个体组成的集合Gk,集合内的k个个体之间具有收敛关系,并且该集合的成员已知,该集合称为核心组。增加一个个体到核心组,组成集合Gk+1,为了检验这个新个体是否属于核心组,即与核心组内的k个个体具有收敛关系,只需对Gk+1进行收敛检验,如果检验结果并不显著为负,说明新的个体属于该集合,logt的参数取决于k的数量和个体的离散程度。
通过观察最后一个观测值或者最后一段时间序列的均值可以构建核心组Gk,将这些观测值从高到底排序,选择前k个值组成一组,这里{k=2,3,…,N},Gk={1,2,…,k}。对Gk的所有子集进行logt回归检验,将每个检验统计量记为tk。然后找到使tk最大的k*,并且满足tk*>c,这里c是一个主观设定的标准,c越大表明俱乐部收敛关系更紧密,发散的概率越小。通过上述步骤可以找到Gk。对剩余部分重复上述步骤可以寻找到剩余的俱乐部,俱乐部收敛的具体算法和停止规则如下。
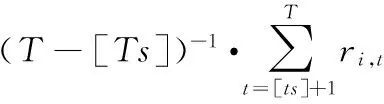
步骤2 建立核心组,选择面板数据最后的观测值里从高到低的顺序前k个观测值建立Gk,这里2≤k
5 实证分析
中国融资融券业务发展迅速,从试点期时的50只股票,到2010年4月业务正式开展时达到90只。第1次扩容是在2011年11月,融资融券标的扩展到285只,不仅包含沪、深两市的股票,还包括华泰柏瑞红利ETF等7只ETF。此后陆续有ETF成为融资融券标的,丰富了交易品种,提供更多的套利空间。随着业务迅速发展,2013年1月和2013年9月又分别进行两次扩容,第5次扩容是2014年9月,融资融券标的股票已经扩展到900只股票、15只ETF,2015年上半年ETF数量增加至19只。转融通业务的开展为统计套利提供了较好的制度安排和交易平台,统计套利在中国市场可行性如何,标的扩容是否增加了套利机会,双向交易机制是否提高了市场效率、降低了统计套利的风险,研究上述问题具有理论意义和实际意义。
5.1 数据处理
统计套利成功的前提假设是价差收敛,如果一组股票的价格具有稳定关系,那么当其中某只股票收益过高或过低时,认为这种异常现象不可持久,卖空高估股,买入低估股,分别建立相反的头寸,待高估和低估的价格被市场机制纠正,价格收敛后分别进行反方向交易结束头寸,组合的收益则取决于价差收敛的幅度和速度。
就单只股票建立多头头寸,相对于基准日的收益为
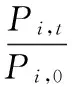
(11)
其中,ri,t为股票i第t个交易日的日内收益率;Pi,t为股票i在第t个交易日的收盘价;Pi,0为基期当日收盘价,本研究以个股或ETF加入融资融券标的生效日之前的最后一个交易日作为基期。参照Roll等[36]的数据处理方法,以2010年4月业务正式开展以来所有融资融券股票为研究对象,对数据采取两个维度划分。由于融资融券标的分阶段扩容,首先根据个股(或ETF)加入融资融券标的的时间分组,同时为了保证统计套利标的股之间收益率的匹配性和系统风险提取的准确性,对个股参照wind公司的行业标准进行分类,所有ETF作为一组。对数据整体进行两个维度的分组,目的是排除加入融资融券标的时间不同和行业风险不同对价格的影响,阶段和行业划分以及每一组样本的具体情况见表1。首先,本研究收集每一组股票和基金的日回报率数据,为避免分红、高送转等情况对收益率的影响,采用向前复权的方式排除除权对股票价格的影响。其次,为避免停牌、恢复上市首日涨跌幅异常值夸大了价格非收敛的可能性和对检验结果的干扰,对以加入融资融券前一个交易日的收盘价为基准计算的定基收益率ri,t采用卡尔曼滤波进行平滑处理。本研究通过极大似然因子分析确定影响收益率变化的因子个数,由于按照行业分组,所以组内所有个股(或基金)提取的系统风险因子唯一,从而确定因子负荷δi,t。
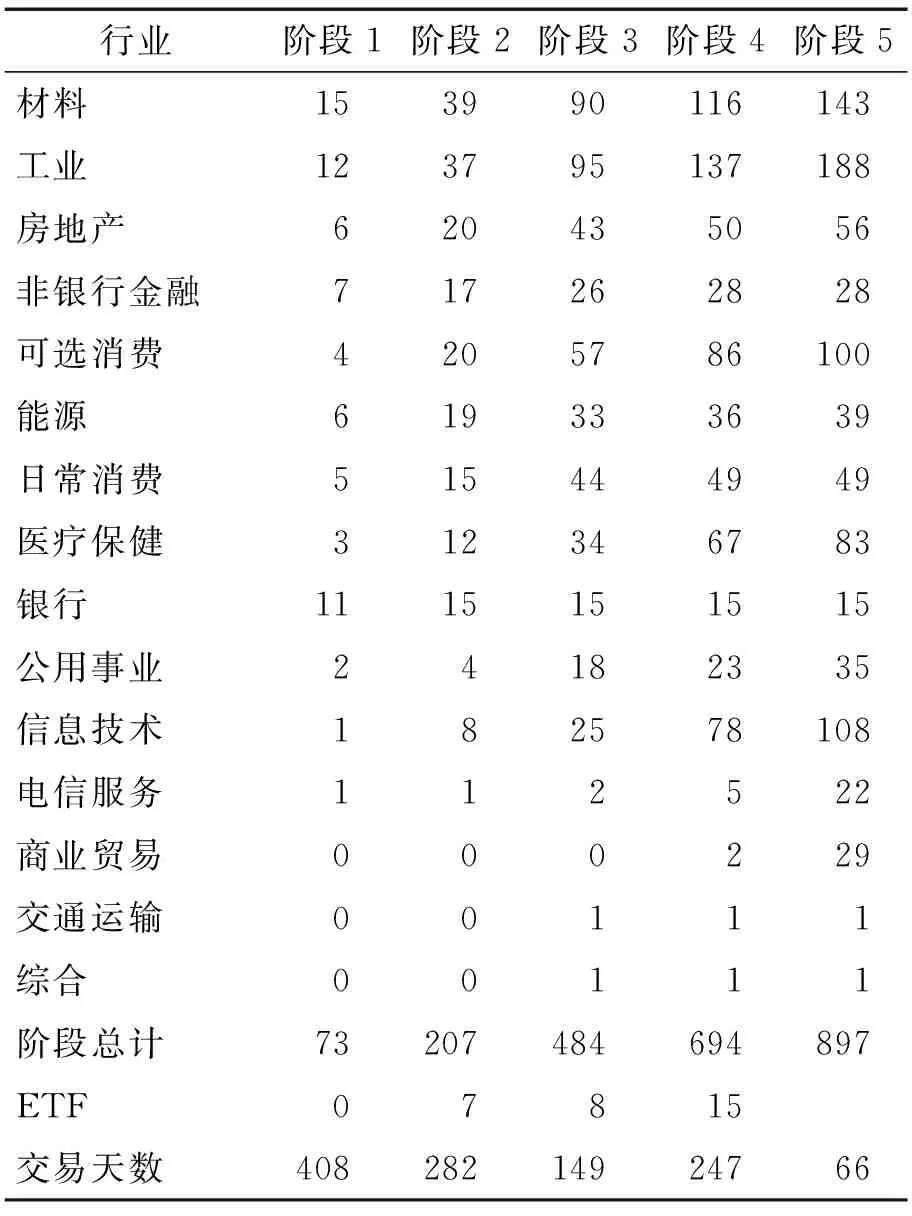
表1 行业、扩容阶段划分及样本内个股数量Table 1 Industry, Phases Division and Numbers of Stocks
对于表1样本说明如下。①因不能持续满足融资融券标的而随后退出标的的证券不在研究范围之内;ETF作为融资融券标的是不定期调整的,在检验时部分ETF检验的时间范围与其加入时间略有差异,而且ETF的时间划分与股票有所不同。②融资融券业务正式开展于2010年4月,第1次融资融券标的扩容生效日为2011年12月5日,从原来的90只标的扩大到285只。本研究将ETF单独进行检验。第1批融资融券标的的样本取自2010年4月1日至2011年12月2日,共408个交易日。第2次融资融券标的扩容生效日在2013年1月31日,因此第2阶段融资融券标的样本取自2011年12月5日至2013年1月30日,共282个交易日。第3次融资融券标的扩容是在2013年9月16日,所以第3阶段融资融券标的样本取自2013年1月31日至2013年9月13日,共149个交易日。第4次融资融券标的扩容生效日是2014年9月22日,所以第4阶段融资融券标的样本取自2013年9月16日至2014年9月19日,共247个交易日。第5阶段自2014年9月22日至2014年12月29日共66个交易日。③南方中证500ETF(510500)于2013年5月27日加入融资融券标的,所以第1阶段的基金检验结果的数据区间取自2011年12月5日至2013年5月24日,共356个交易日;第2阶段从2013年5月27日至2014年5月30日,共246个交易日;第3阶段自2014年6月1日至2014年12月29日,共146个交易日。2013年7月31日,恒生ETF(159920)、嘉实中证500ETF(159922)被剔除,因而本研究不包含这两只ETF。
5.2 logt检验
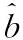
观察收敛检验结果,首先,从行业整体看,个股收敛的原假设被拒绝的概率较大;从各个行业每个阶段的表现看,融资融券标的扩容给统计套利资产组合的选择增加了难度和风险。随着标的扩容,行业整体的收敛关系非常少见,大部分行业股价在整个样本阶段始终发散。只有在融资融券业务开展初期,工业、房地产、非银行金融业和可选消费个股收敛,大部分行业在融资融券标的扩容后股票价格由收敛变为发散。可见除ETF和银行业以外,标的数量的增加无益于降低统计套利的风险。从行业整体来说,价差发散是大概率事件,仅仅根据所属行业选择股票进行统计套利存在很高风险,这也反映了市场有效性不足。
其次,自第2阶段起有ETF加入融资融券标的,与股票不同的是考虑新增ETF在内,ETF整体仍保持收敛关系,说明ETF相比于股票来说是更为理想的套利标的。主要原因在于,①融资融券标的ETF以指数型基金为主,ETF的特点是被动的复制指数成份组合,因而其波动具有同质性,价格收敛关系较为稳定。②ETF的发行规模大,可融券源较广,与股票做空相比,ETF更为便利。③ETF具有更完善的交易机制,存在多种套利模式,T+0的交易机制提供了更多的套利机会,降低了风险。ETF可以与一揽子股票进行折溢价套利,而且ETF可以与沪深300期货和上证50股指期货之间对冲,价格异常值可以迅速被投资者通过交易机制纠正,因而定价效率高。④ETF的交易费用较低,流动性更好,因此投资者将ETF作为统计套利组合比股票交易成本更低,选择ETF进行统计套利更有效。
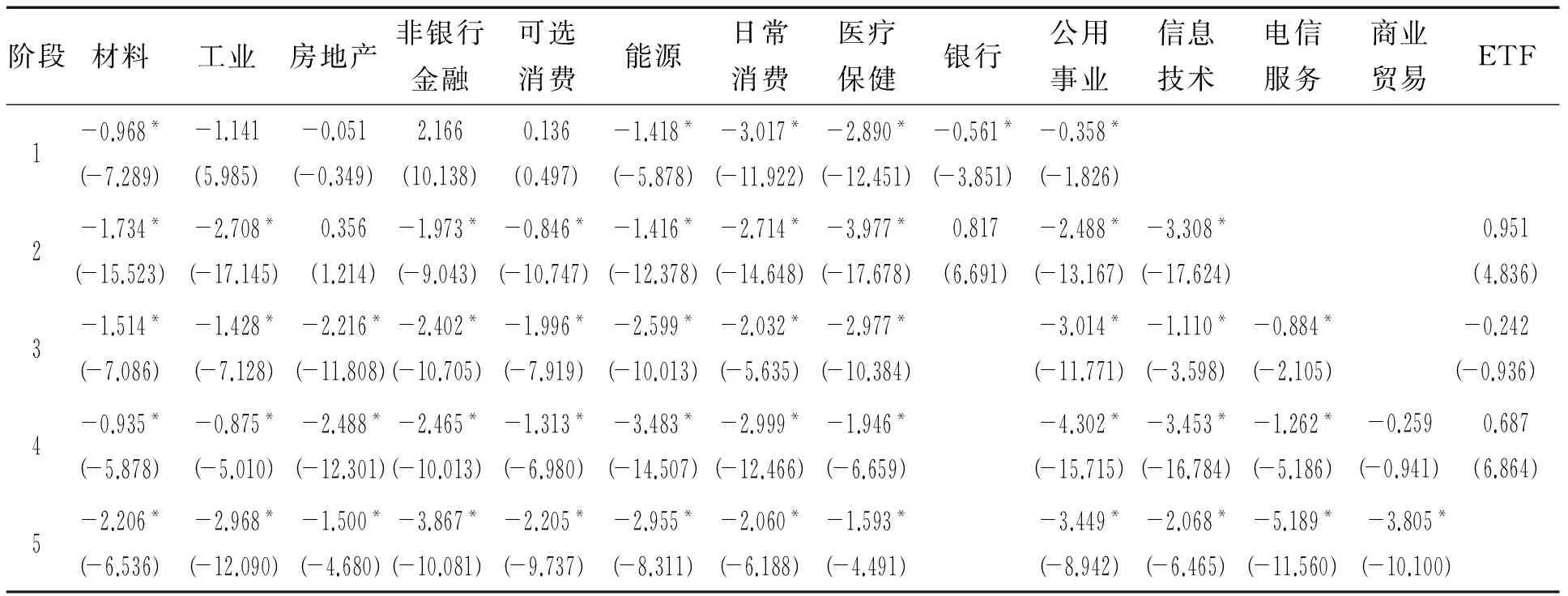
表2 logt 检验结果Table 2 Results of logt Test
注:括号内数据为t值,*为5%显著性水平下拒绝原假设,本研究中k=5。

图1 融资融券交易统计(期间买入额和期间卖出额)Figure 1 Statistics of Margin Trading(Long and Short Amount during the Period)
从各个阶段各行业融资融券标的股收敛情况的对比看,第1批融资融券标的整体收敛水平相对较好,套利风险较小,但是从第2阶段及以后的检验结果看,除银行业外股价收敛的关系不复存在。这反映出目前中国市场的套利交易不足,杠杆交易机制和做空机制没有充分发挥,这与有效的证券借贷市场缺位有关。目前中国融资融券业务开展尚存在诸多需要完善之处。一方面交易成本过高,证监会指导意见规定融资成本不低于央行规定的同期金融机构贷款基准利率,各家券商在此基础上自主决定上浮的幅度,平均成本约为8.350%~8.600%,较高的成本压缩了套利利润,从而阻碍了套利交易。另一方面,可融券较少,业务开展初期,可融券源主要是证券公司自营账户中的标的证券,极大地限制了做空交易,妨碍了融资融券业务的价格发现功能,这与廖士光[39]和许红伟等[28]的研究结论一致。此外,中国股票市场长期以来缺乏做空机制,投资者形成了比较严重的做多思维,融资便利和融券困难使投资者将融资融券业务单一的理解为融资买股,放大杠杆,图1给出自融资融券业务开展以来业务规模的发展情况。
从图1融资融券成交统计情况看,融资融券业务近年来发展非常迅速,但是严重不平衡,融资买入额远高于融券卖出额,做空机制没有充分发挥,影响了其提高市场效率功能的发挥,同时妨碍了套利交易的进行,并增加套利交易风险,一定程度上失去了应有的意义。
5.3 俱乐部收敛检验结果
从行业整体看,标的股价格不收敛意味同一行业内并非任意两只融资融券标的股票存在收敛关系,但这并不否认统计套利的可行性,通过对行业内个股进行进一步的检验可以寻找具有收敛关系的股票。本研究对每一时间段每个行业的股票组合进行俱乐部收敛检验,经检验发现每个行业都存在数量不一、规模不等的俱乐部,结果见表3。
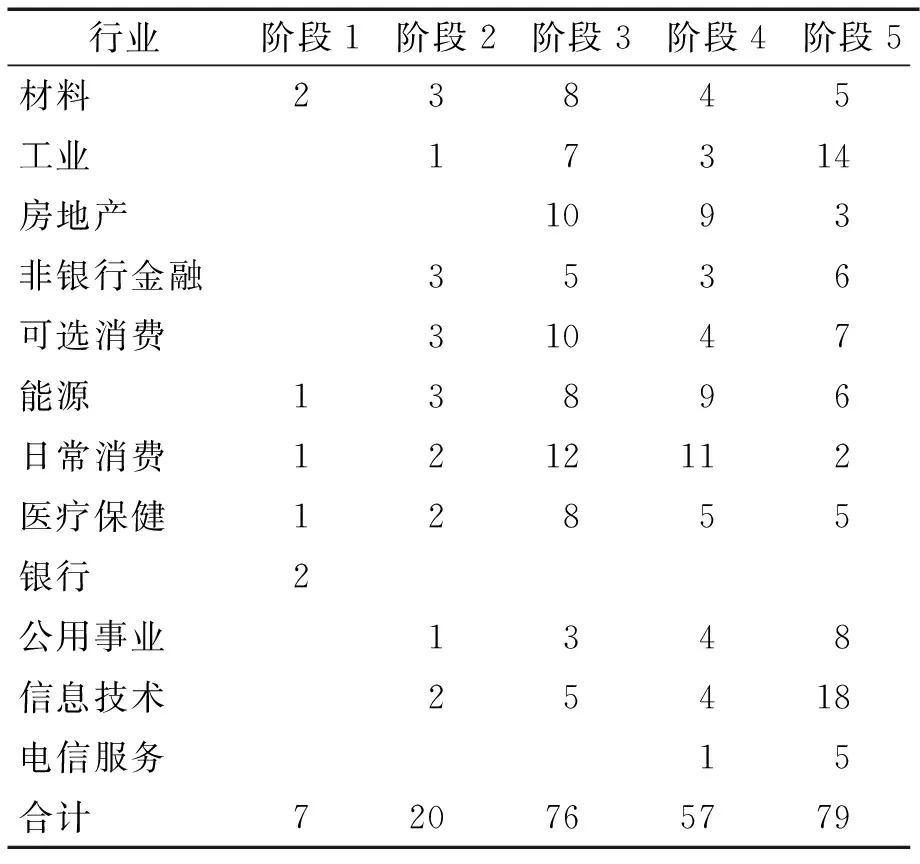
表3 各行业分阶段俱乐部数量Table 3 Club Convergence Result of All Sectors and Phases
注:第1阶段中工业、房地产、非银行金融、可选消费行业整体具有收敛关系;第2阶段中房地产和银行业整体具有收敛关系,因而不对其进行俱乐部收敛检验;ETF在整个样本区间具有收敛关系,因而不对其进行俱乐部检验。
从俱乐部收敛的检验结果看,标的股票扩容既增加了套利的风险也增加了套利的机会。俱乐部收敛的现象非常普遍,在不同行业和不同阶段都存在一定的统计套利的交易机会,俱乐部内的股票具有明显的价差收敛关系,而且融资融券标的第1次扩容以后每一行业内的俱乐部数量均有所增加,说明虽然行业总体来看标的股收敛的原假设被拒绝,但经过俱乐部收敛检验仍可以找到统计套利组合。
首先,统计套利策略在中国市场具有可行性,扩容后样本范围内所有行业内部都存在具有收敛关系的俱乐部。某些行业包含了较多的融资融券标的,如工业、材料、可选消费、医疗保健,而这些行业内部可以按照公司所属二级行业进一步细分。行业属性在一定程度上决定了股票之间的俱乐部关系,同一细分行业内的股票价差收敛的概率更大。此外,所有融资融券标的ETF都可以作为统计套利的资产组合,收敛关系在整个样本范围内保持稳定。
其次,融资融券标的扩容既增加了统计套利的机会,也增加了套利风险,融资融券标的扩容并不能保证行业整体的收敛性提高,一个重要的原因是新增标的与原有标的差异较大,同时投资者对新增标的进行投机,导致价格虚高,增加了套利风险。中国股市“小盘股效应”非常明显,第2次扩容首次加入6只创业板股票,第3次扩容中小板和创业板分别增加57只和28只股票,占深市新增102只标的总量的80%。而这些个股在加入到两融标的之后出现大幅溢价,6只新增创业板标的中华谊兄弟、碧水源、机器人和蒙草抗旱创出了上市以来的新高。自加入融资融券标的至2013年9月6日,华谊兄弟融资买入成交额112.463亿元,占成交总额的17.584%。鹏博士在2013年5月1日至9月11日这段区间上涨超过75%,融资买入额占成交总额高达20.167%,成为此期间两市买入成交额最高的股票。从2013年上半年融资融券交易统计数据看,创业板标的股票融资买入额占成交额比重明显提升,换手率也大幅提高,说明市场对创业板标的股票加入融资融券标的大肆投机造成这类股票超额收益率畸高。此外,中小市值个股因流动性较差存在一定的风险溢价,所以这类个股加入到融资融券标的之后并不能与其他个股构建统计套利组合,从俱乐部内股票成分看,创业板个股最少,中小板次之。限于篇幅,俱乐部收敛的具体结果不一一汇报,仅在表4和表5列出医疗保健行业和非银行金融业俱乐部收敛检验结果,感兴趣的读者可向作者索要。
通过每个行业不同时间段俱乐部内的个股组成之间的对比分析发现(限于篇幅,未列出所有行业的俱乐部收敛结果,感兴趣的读者可向作者索要),俱乐部收敛关系不稳定。一方面,就某一行业来说,随着融资融券标的增加,俱乐部的数量有所增加,但规模并非与新增标的数量呈正比,其数量不稳定。另一方面,不同阶段不同行业都存在俱乐部收敛,但俱乐部收敛关系可能发生变化,俱乐部内的成员并不稳定。例如,在第1阶段的7个俱乐部里仅有600028、601857、000568和000858在第2阶段仍具有收敛关系(受篇幅限制,未列出所有行业的俱乐部收敛结果,感兴趣的读者可向作者索要)。由表4可知,医疗保健行业的000538和600196在第2阶段和第3阶段都保持着收敛关系,但第4阶段收敛关系不存在,而在第5阶段又恢复了收敛关系。因而,以从历史走势关系推断出来的个股之间的价差收敛关系作为构建套利组合的方法,具有一定的借鉴意义,但存在较大不确定性,投资者需要动态调整套利组合,因此套利风险较大。
套利风险较高说明市场的有效性不足,原因之一在于双向交易机制没有充分发挥,做空机制能够提高股票定价效率和市场有效性,但并不会造成市场不稳定[40],因而发展融资融券业务、完善双向交易机制对市场具有重要意义,在增加融资融券标的的同时应完善融资和融券平台的建设。目前中国融资融券的交易成本由证监会指导形成,市场化价格形成机制缺位,限制了融资融券业务发挥稳定市场的功能。在市场化的价格形成体系下,借贷利率由供给方和需求方通过竞争和交易形成,市场大涨时投资者融资需求增加、融券需求减少,融资成本提高而融券成本降低,有助于抑制大盘暴涨。反之,当市场大幅下跌时,融券需求增加、融资需求减少,可融券减少而可贷资金增加,融券成本提高而融资成本降低,有助于抑制大盘暴跌。因此,目前中国应尽快形成资金和证券的交易市场,允许资金和证券的出借人和借入人在统一的市场交易平台上通过交易和竞争形成市场化的融资融券费率和期限,提高成交效率,充分发挥融资融券业务的功能,并为套利交易提供便利。
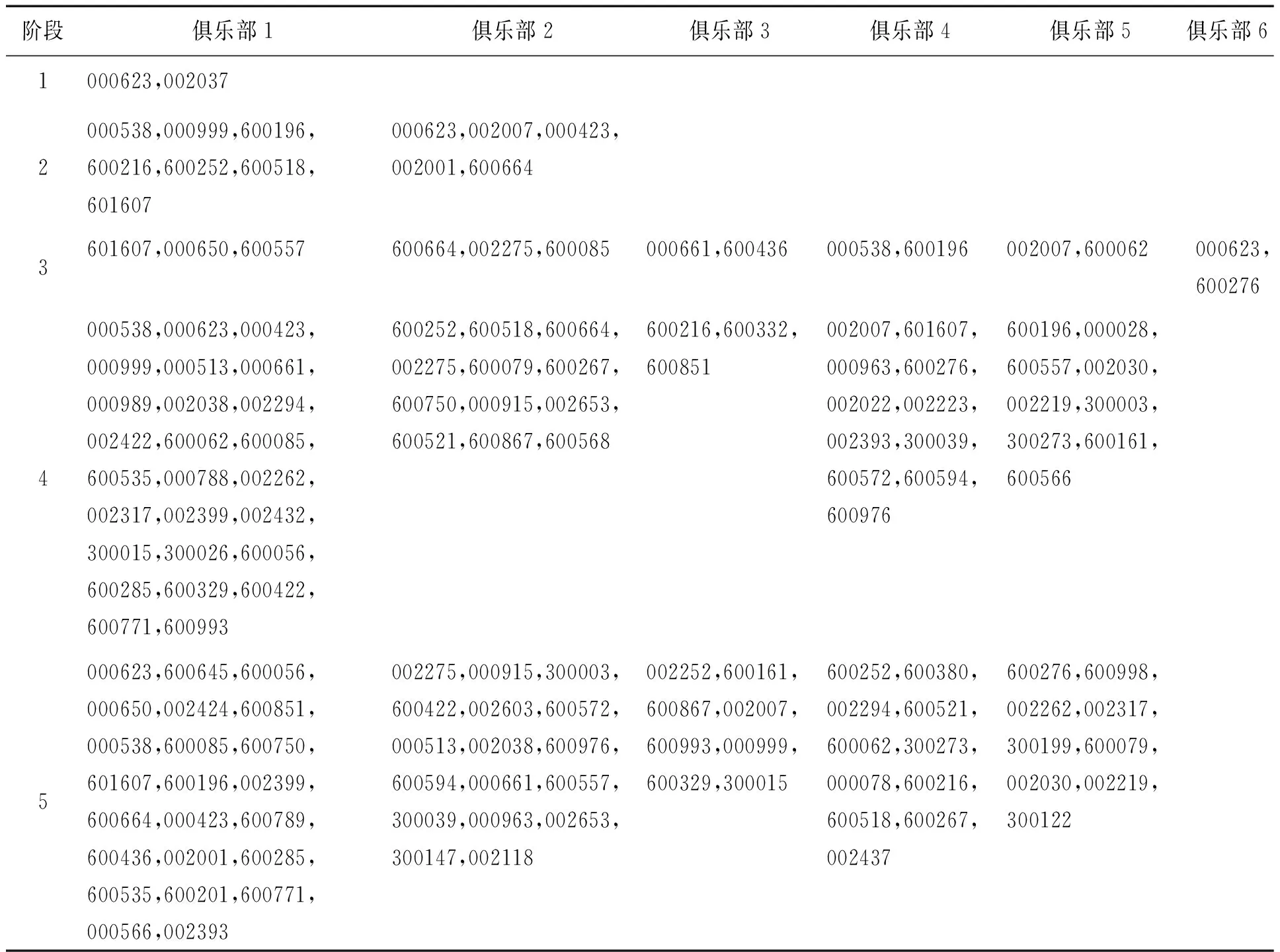
表4 医疗保健行业俱乐部收敛结果Table 4 Club Convergence Result of Healthcare Sector
注:未列出的股票与其他股票之间不存在俱乐部收敛关系,下同。
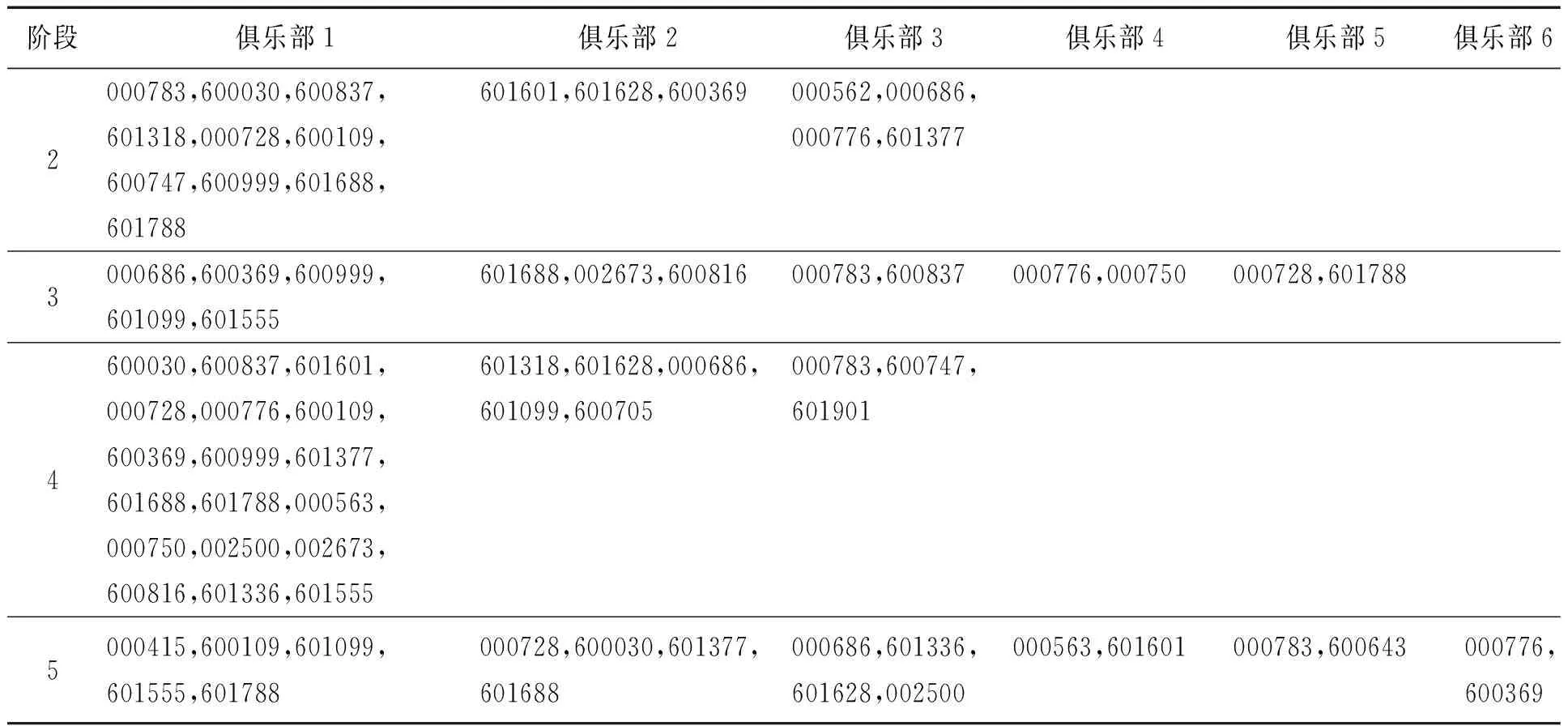
表5 非银行金融业俱乐部收敛结果Table 5 Club Convergence Result of Non-Bank Financial Sector
注:第1阶段非银行金融业没有俱乐部。
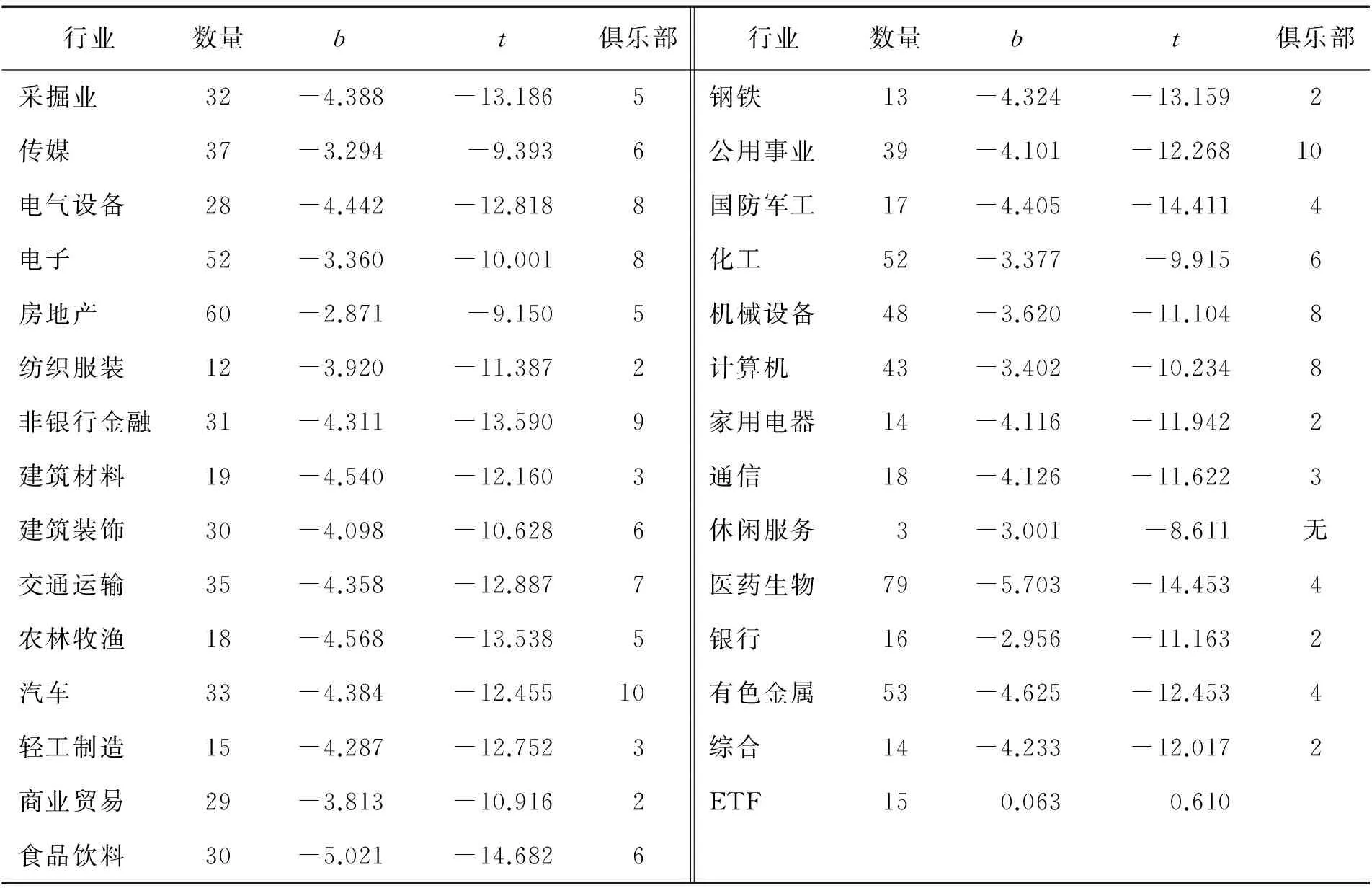
表6 样本外检验和俱乐部分析Table 6 Out of Sample Test and Club Convergence Analysis
注:融资融券标的ETF在2015年2月、4月、5月新增了4只,由于时间较短不在本研究考虑范围内,ETF整体具有收敛关系,因而不对其进行俱乐部收敛检验。
6 样本外检验
为了进一步分析统计套利的风险,验证同一行业不同个股的价格关系,本研究采用2015年1月5日至2015年5月29日剔除停盘时间超过1个月后的870只融资融券标的股票和15只标的ETF进行样本外检验,数据来源于wind数据库。样本的分组方法采用申万一级行业分类,采用与前文同样的处理方法,将向前复权后的股票和ETF收盘价转换为以2015年1月5日为基期的定基收益率,按照(10)式进行logt收敛检验并进行俱乐部收敛分析,表6给出行业分组情况、回归系数、相应的t统计量和每个行业的俱乐部数量。
logt收敛结果证明了前文的判断,统计套利存在较大风险,但仍具有可行性。从行业整体看,个股之间发散,值得注意的是在样本外检验中,在前文第2阶段以来一直保持行业整体收敛的银行业个股的收敛关系不复存在,但ETF之间的收敛关系仍然稳定,更适合进行统计套利。样本外俱乐部收敛检验结果表明,行业内普遍存在由价格收敛的个股组成的俱乐部,不同行业的俱乐部数量差别较大,但并非与行业内股票数量严格成正比。俱乐部的规模变化没有明显规律,一般来说俱乐部规模较大,所在行业的股票数量较多,但反之不成立。进一步的,由于房地产,银行,医药生物、非银行金融、通信等行业按照申万一级行业分类与wind行业分类相近,为了验证不同行业划分方法对俱乐部收敛关系的影响,本研究按照两种分类方法得到的2个阶段的俱乐部进行对比,限于篇幅仅在表7报告中医药生物和非银行金融业的对比结果。
通过与前文第5期的俱乐部进行对比,从各行业的俱乐部整体看,股票之间的收敛关系不稳定,根据历史交易数据构建的套利组合可能导致策略失败。但是某些行业俱乐部内存在具有比较稳定的收敛关系的个股,根据俱乐部选择套利资产仍具有一定的参考意义。对于非银行金融业来说,2014年9月至12月的俱乐部在2015年上半年不复存在。但就医药生物行业而言,如000078、600380和600518在前文第5阶段的俱乐部收敛分析中存在收敛关系,这种关系在样本外检验中仍然存在。同样,002030在前文第5阶段与300199存在收敛关系,而这种关系在样本外检验仍然存在。样本外检验表明,不同行业的俱乐部的稳定性差异较大,房地产行业个股的俱乐部收敛关系较为稳定,非银行金融业个股的俱乐部收敛关系稳定性最差。总体来说,采用新的行业分组方法得到的俱乐部与上一期相比仍然存在较多的交集,也即某些股票之间存在具有比较稳定的收敛关系,可以作为套利资产。
为了进一步检验依据俱乐部收敛检验结果选择统计套利资产组合的可行性,本研究对表7中与上一期相比仍然具有收敛关系的股票、所有ETF以及样本外检验得到的其他俱乐部的股票,在原有样本时间范围上增加2015年6月1日至6月20日的交易数据进行收敛检验和分析,发现这些股票仍保持了收敛关系,也即在历史上具有较稳定的收敛关系的股票组合可以在未来较短的时间内保持收敛关系。样本外分析结果表明,虽然统计套利存在较大风险,投资组合的选择和构建存在较大难度,但仍存在较多套利机会,具有长时间稳定的收敛关系的股票组合仍可以在一定时间范围内具有参考价值。因而统计套利策略在中国市场具有一定可行性,将俱乐部收敛分析作为构造套利组合的依据具有一定的价值和可操作性。
表7医药生物和非银行金融业样本外俱乐部收敛结果
Table7ResultofOutofSampleClubConvergenceofMedicalBiologyandNon-Banking

样本外俱乐部收敛分析对比分析申万行业俱乐部序号俱乐部内股票序号在第5阶段按wind行业分类收敛且在样本外检验中保持收敛关系的股票组合医药生物1000078,000566,002030,300199,300216,600380,6005181-1002030,3001991-2000078,600380,6005182000790,002022,002219,002223,002424,300147,600222,600572,600645,600771,600789,6008672-1300147,6005722-2002424,600645,600771,6007893000028,000513,000650,000915,002007,002118,002317,002603,300003,300015,300039,300122,300273,600085,600161,600252,600276,600285,600329,600436,600521,600587,600594,600750,600993,600998,6016073-1000650,600085,600285,600436,600750,6016073-2000513,000915,002118,002603,300003,300039,6005943-3002007,300015,600161,600329,6009933-4300273,600252,6005213-5002317,300122,6009984000028,000513,000650,000915,002007,002118,002317,002603,300003,300015,300039,300122,300273,600085,600161,600252,600276,600285,600329,600436,600521,600587,600594,600750,600993,600998,6016074-1000423,000623,002001,002393,002399,6001964-2000661,000963,002038,002275,002653,600422,6009764-3000999,0022524-4002294,002437,600062,600216,6002674-5002262,600079非银行金融1600643,600705,6008302600635,6016283600816,6013364600109,6016015000415,0005636000415,0005637002500,6013188000686,000776,002673,6015559000686,000776,002673,601555无
注:按照申万的一级行业分类标准,医药生物行业与wind行业分类的医疗保健行业的个股最为接近。前3列给出按照申万行业分组的俱乐部收敛分析结果,医药生物行业有4个俱乐部,非银行金融业有9个俱乐部。第4列和第5列给出对比结果,序号1-1表示样本外检验得到的第1个俱乐部中与第5阶段按照wind行业分类得到的俱乐部(见表4和表5最后1行)相比仍然存在收敛关系的第1个股票组合。
7 结论
本研究基于沪深两市融资融券标的股和ETF的日内交易数据,按照上市公司所属行业和融资融券标的分阶段扩容的时间进行两个维度分组,采用Phillips等[34]的转移模型进行价差收敛性检验。研究结果表明,①依据行业选择套利股票组合风险较大,同一行业的个股以融资融券标的扩容时间划分的不同时间段内价格发散的情况更为普遍。融资融券的杠杆交易和双向交易机制尚未充分发挥,市场有效性不足,统计套利风险较大。②行业内存在具有价格收敛关系的个股组合,本研究将这种关系称之为俱乐部收敛。融资融券标的扩容既增加了套利的机会也增加了套利的风险,随着融资融券标的扩容,俱乐部数量有所增加,但是俱乐部并不稳定,统计套利资产组合的选择和构建具有较大难度。俱乐部收敛检验对选择套利资产组合具有一定参考价值,依据俱乐部收敛关系构建统计套利资产组合必须对组合进行动态调整。③相对于融资融券标的股票来说,ETF收敛关系稳定,更适合作为统计套利的资产组合。总体来说,虽然统计套利在A股市场具有较大风险,但仍具有可行性,基于样本外检验的结果证实了上述判断。
本研究的创新在于,首先,利用中国融资融券标的日内交易数据全面系统地研究价差是否收敛这一关键问题,通过转移模型分析标的证券价格收敛关系的变化,发现统计套利存在较大风险,并在一定程度上证明了市场有效性不足。其次,实证分析发现某些股票之间存在俱乐部收敛关系,而ETF具有稳定的收敛关系。统计套利在A股市场仍然具有可行性,俱乐部收敛检验能够为选择资产组合提供一定参考。
为加快融资融券业务发展,提高市场的定价效率,本研究建议:①降低融资融券交易的成本,在风险可控的前提下适当提高交易杠杆,促进市场发展和提升交易活跃度。②改革资金和证券的价格形成市场机制,建立融资融券业务资金和证券的交易市场,形成市场化的资金和证券借贷机制,提高交易效率,充分发挥融资融券业务稳定市场的功能。
本研究存在一些不足之处有待完善。首先,本研究仅能为统计套利资产组合的选择提供依据和借鉴,由于俱乐部收敛关系不稳定,尚不能形成具有稳定回报的交易策略。其次,依据俱乐部收敛构建投资组合还需要考虑投资组合的权重、交易成本、风险控制以及因停牌、现金股利等诸多因素对投资组合的影响,投资组合动态调整的频率和具体方法等诸多问题作为交易策略实际应用还有待深入研究。
[1]Bhattacharya R R,O′ Brien S J.Arbitrage risk and market efficiency:Applications to securities class actions[R].Santa Clara,CA:Santa Clara Law Review,2015.
[2]Hogan S,Jarrow R,Teo M,Warachka M.Testing market efficiency using statistical arbitrage with applications to momentum and value strategies[J].Journal of Financial Economics,2004,73(3):525-565.
[3]Jarrow R,Teo M,Tse Y K,Warachka M.An improved test for statistical arbitrage[J].Journal of Financial Markets,2012,15(1):47-80.
[4]Rad H,Low R K Y,Faff R W.The profitability of pairs trading strategies:Distance,cointegration,and copula methods[R].Brisbane QLD:The University of Queensland,2015.
[5]Bondarenko O.Statistical arbitrage and securities prices[J].The Review of Financial Studies,2003,16(3):875-919.
[6]D′Avolio G M.The market for borrowing stock[J].Journal of Financial Economics,2002,66(2/3):271-306.
[7]Lamont O A,Thaler R H.Can the market add and subtract?Mispricing in tech stock carve-outs[J].Journal of Political Economy,2003,111(2):227-268.
[8]Duffie D,Garleanu N,Pedersen L H.Securities lending,shorting,and pricing[J].Journal of Financial Economics,2002,66(2/3):307-339.
[9]Kiyotaki N,Moore J.Credit cycles[J].Journal of Political Economy,1997,105(2):211-248.
[10] Gromb D,Vayanos D.Equilibrium and welfare in markets with financially constrained arbitrageurs[J].Journal of Financial Economics,2002,66(2/3):361-407.
[11] Brunnermeier M K,Pedersen L H.Market liquidity and funding liquidity[J].The Review of Financial Studies,2007,22(6):2201-2238.
[12] Garleanu N,Pedersen L H.Margin-based asset pricing and deviations from the law of one price[J].The Review of Financial Studies,2011,24(6):1980-2022.
[13] Fostel A,Geanakoplos J.Leverage cycles and the anxious economy[J].The American Economic Review,2008,98(4):1211-1244.
[14] Basak S,Croitoru B.Equilibrium mispricing in a capital market with portfolio constraints[J].The Review of Financial Studies,2000,13(3):715-748.
[15] Basak S,Croitoru B.On the role of arbitrageurs in rational markets[J].Journal of Financial Economics,2006,81(1):143-173.
[16] Xiong W.Convergence trading with wealth effects:An amplification mechanism in financial markets[J].Journal of Financial Economics,2001,62(2):247-292.
[17] Kyle A S,Xiong W.Contagion as a wealth effect[J].The Journal of Finance,2001,56(4):1401-1440.
[18] Kondor P.Risk in dynamic arbitrage:The price effects of convergence trading[J].The Journal of Finance,2009,64(2):631-655.
[19] Miao G J.High frequency and dynamic pairs trading based on statistical arbitrage using a two-stage correlation and cointegration approach[J].International Journal of Economics and Finance,2014,6(3):96-110.
[20] Huck N,Afawubo K.Pairs trading and selection methods:Is cointegration superior?[J].Applied Economics,2015,47(6):599-613.
[21] 温予群,刘洪光.基于沪深300的统计套利的实证研究[J].金融经济,2011(12):69-71.
Wen Yuqun,Liu Hongguang.Empirical research on statistical arbitrage based on Shanghai and Shenzhen 300 stock index futures[J].Finance & Economy,2011(12):69-71.(in Chinese)
[22] 李乐,张淳奕,杨之曙.基于沪深300股指期货合约的日内高频跨期统计套利策略[J].清华大学学报:自然科学版,2014,54(8):1080-1086.
Li Le,Zhang Chunyi,Yang Zhishu.Statistical calendar spread arbitrage strategy using intraday high frequency data of the Shanghai and Shenzhen 300 stock index futures[J].Journal of Tsinghua University:Science and Technology,2014,54(8):1080-1086.(in Chinese)
[23] 戴进.基于协整的股指期货和ETF的统计套利[J].中国证券期货,2012(10):1-2.
Dai Jin.Cointegration-based statistical arbitrage on stock index future and ETF[J].Securities & Futures of China,2012(10):1-2.(in Chinese)
[24] 方昊.统计套利的理论模式及应用分析:基于中国封闭式基金市场的检验[J].统计与决策,2005(12):14-16.
Fang Hao.Statistical arbitrage theoretical mode and application analysis based on the test of Chinese close fund market[J].Statistics and Decision,2005(12):14-16.(in Chinese)
[25] 吴振翔,魏先华,陈敏.基于统计套利的开放式基金评级[J].管理评论,2009,21(6):3-9.
Wu Zhenxiang,Wei Xianhua,Chen Min.Open-end fund rating based on statistical arbitrage[J].Management Review,2009,21(6):3-9.(in Chinese)
[26] 陈怡.统计套利策略在我国分级基金市场的尝试[J].科学技术与工程,2012,12(3):724-729.
Chen Yi.The trading strategy of split-funds based on statistical arbitrage[J].Science Technology and Engineering,2012,12(3):724-729.(in Chinese)
[27] 李科,徐龙炳,朱伟骅.卖空限制与股票错误定价:融资融券制度的证据[J].经济研究,2014,49(10):165-178.
Li Ke,Xu Longbing,Zhu Weihua.Short-sale constrains and stock mispricing:The evidences from the margin transactions institution[J].Economic Research Journal,2014,49(10):165-178.(in Chinese)
[28] 许红伟,陈欣.我国推出融资融券交易促进了标的股票的定价效率吗?基于双重差分模型的实证研究[J].管理世界,2012(5):52-61.
Xu Hongwei,Chen Xin.Has the introduction of margin trading in China promoted the pricing efficiency of underlying stocks?[J].Management World,2012(5):52-61.(in Chinese)
[29] 肖浩,孔爱国.融资融券对股价特质性波动的影响机理研究:基于双重差分模型的检验[J].管理世界,2014(8):30-43.
Xiao Hao,Kong Aiguo.A study on the securities margin trading on the fluctuations of the stock price′s special nature:A test based on the difference-in-difference model[J].Management World,2014(8):30-43.(in Chinese)
[30] 李志生,陈晨,林秉旋.卖空机制提高了中国股票市场的定价效率吗?基于自然实验的证据[J].经济研究,2015,50(4):165-177.
Li Zhisheng,Chen Chen,Lin Bingxuan.Does short selling improve price efficiency in the Chinese stock market?Evidence from natural experiments[J].Economic Research Journal,2015,50(4):165-177.(in Chinese)
[31] 张戡,李婷,李凌飞.基于聚类分析与协整检验的A股市场统计套利策略[J].统计与决策,2012(15):166-169.
Zhang Kan,Li Ting,Li Lingfei.Statistical arbitrage strategy in A share market based on cluster analysis and co-integration analysis[J].Statistics and Decision,2012(15):166-169.(in Chinese)
[32] 雷井生,林莎.基于高频数据的统计套利策略及实证研究[J].科研管理,2013,34(6):138-145.
Lei Jingsheng,Lin Sha.Statistical arbitrage strategies based on high frequency data[J].Science Research Management,2013,34(6):138-145.(in Chinese)
[33] 高兴波,郭甲蕾,胡智磊.统计套利策略在对冲基金投资中的应用研究[J].中央财经大学学报,2014(6):31-37.
Gao Xingbo,Guo Jialei,Hu Zhilei.Application analysis of statistical arbitrage strategy in hedge funds[J].Journal of Central University of Finance & Economics,2014(6):31-37.(in Chinese)
[34] Phillips P C B,Sul D.Transition modeling and econometric convergence tests[J].Econometrica,2007,75(6):1771-1855.
[35] Chamberlain G.Funds,factors,and diversification in arbitrage pricing models[J].Econometrica,1983,51(5):1305-1323.
[36] Roll R,Ross S A.An empirical investigation of the arbitrage pricing theory[J].The Journal of Finance,1980,35(5):1073-1103.
[37] Apergis N,Christou C,Miller S M.Country and industry convergence of equity markets:International evidence from club convergence and clustering[J].The North American Journal of Economics and Finance,2013,29:36-58.
[38] Perlin M,Dufour A,Brooks C.The determinants of a cross market arbitrage opportunity:Theory and evidence for the European bond market[J].Annals of Finance,2014,10(3):457-480.
[39] 廖士光.融资融券交易价格发现功能研究:基于标的证券确定与调整的视角[J].上海立信会计学院学报,2011,25(1):67-76.
Liao Shiguang.Study on the price discovery of margin purchase and short sale transaction:From the perspective of underlying securities determination and adjustment[J].Journal of Shanghai Lixin University of Commerce,2011,25(1):67-76.(in Chinese)
[40] Saffi P A C,Sigurdsson K.Price efficiency and short selling[J].The Review of Financial Studies,2011,24(3):821-852.
EmpiricalStudyontheRiskofStatisticalArbitrageinA-shareMarket
Zhao Shengmin,Yan Honglei
School of Finance, Nankai University, Tianjin 300071, China
Statistical arbitrage, theoretically is riskless, however the prices of the assets might diverge, forcing investors who exploit the relative mispricing of assets to unwind some of their positions at spectacular loss. Convergence of the arbitrage assets' prices is a fundamental issue of statistical arbitrage since the unsteady convergence relationship between arbitrage assets causes arbitrage risk, cost as well as expected return of arbitrage. Based on transition model proposed by Phillips and Sul (2007), this paper studies convergence among the securities eligible for margin trading in A share market, and analyzes the risk of statistical arbitrage.
With the empirical study on the trading data of all the securities eligible for margin trading from April 2010 to June 2015, we find constructing portfolio solely by stocks′ sector is risky, and high risk of arbitrage implies the market lacks efficiency as the market is inefficient in correcting the mispricing, which is consistent with intuition. However, statistical arbitrage in A-share market is feasible. Result shows that the stocks of identical sectors as a whole do not converge steadily or robustly. Stocks of manufacture, real estate, non-bank finance, etc. converge as a whole through the first phase, but after the expansion of the eligible list of margin trading, convergence in the whole sector diminishes. However, this does not deny the feasibility of statistical arbitrage, the phase-in expansion of eligible list brings opportunities as well as risks since more eligible stocks increase both diversity and complexity of asset selection as some newly added stocks converge with the existing stocks while others do not. By testing the convergence within the sectors, we find certain stocks converge and form subgroups which are referred as club convergence in this paper. Clubs increase with the expansion of eligible list although they do not increase strictly across different phases. Compared with stocks, the ETFs as a whole group converge robustly and the newly added ETFs converge with the existing ETFs across all the phases, which ensure their applicability for statistical arbitrage. Out of sample test confirms the aforementioned findings, and club convergence maintains for a certain period and provide arbitrage opportunities, therefore club convergence test could serve as an instrument for arbitrage portfolios selection.
Margin trading is prevailing and both academicians and practitioner focus on developing arbitrage strategies, yet the risk of arbitrage is ignored. This paper sheds light on the risk of statistical arbitrage and provides empirical evidence for hedge fund. Moreover, we propose applicable methods of constructing arbitrage portfolios. In order to improve market efficiency through margin trading and arbitrage, we suggest the price and quantity of capital and stocks be determined by market competition rather than regulation or arbitrary decision of brokers.
statistical arbitrage;margin trading;transition model;logttest;club convergence
Date:January 18th, 2015
DateJune 20th, 2015
FundedProject:Supported by the Humanity and Social Sciences Research of Ministry of Education(15YJA790090)
Biography:Zhao Shengmin(1967-, Native of Qiqihar, Heilongjiang), Doctor in Engineering and is a Professor in the School of Finance at Nankai University. His research interests include financial engineering and derivative pricing, etc. E-mail:zhaoshengmin@nankai.edu.cn
F832.5
A
10.3969/j.issn.1672-0334.2015.05.008
1672-0334(2015)05-0093-13
2015-01-18修返日期2015-06-20
教育部人文社会科学研究项目(15YJA790090)
赵胜民(1967-),男,黑龙江齐齐哈尔人,工学博士,南开大学金融学院教授,研究方向:金融工程和衍生品定价等。E-mail:zhaoshengmin@nankai.edu.cn
□
