自适应多自由度变稳控制技术研究
2015-12-25邹泉袁东丁团结
邹泉,袁东,2,丁团结
(1.中国飞行试验研究院中航工业飞行仿真航空科技重点实验室,陕西西安710089;2.中国飞行试验研究院试飞员学院,陕西西安710089)
0 引言
空中飞行模拟器,又被称之为变稳飞机,它能够通过变稳电传系统和可变人感系统达到改变本机动力学特性、稳定性和操纵性的目的。目前我国仅有的三自由度变稳飞机IFSTA能够模拟一般的飞行品质特性,但是对于某些飞行品质特别是对航迹角和带直接力控制飞机的飞行品质模拟方面稍显不足;另一方面,由于经典控制技术与飞机状态敏感度较高,当飞机状态发生变化时,如果控制律增益不进行调整,那么原有的跟踪精度将会变差,甚至引起控制系统不稳定,而如果采用增益调度的方式又会带来试飞架次增多等问题。因此,本文在三自由度变稳模型跟踪控制技术的基础上,通过增加直接升力和自动油门控制,采用现代控制理论中的自适应控制技术,以提高模型跟踪控制的模拟能力和控制律的鲁棒性。
1 多自由度变稳控制技术
按照MIL-F-8785C和GJB2874-1997飞行品质规范,任何一架飞机的动态响应品质主要是由等效传递函数中的各模态参数确定的。对纵向来说,在不考虑长周期运动时,等效传递函数主要包括q/Fe,nz/q和nz/α;对于横航向来说,主要包括p/Fa和β/Fr。如果空中飞行模拟能够模拟这些等效传递函数或达到相似模拟,其结果就是正确的[1]。对于三自由度变稳飞机IFSTA而言,横航向是可以对等效传递函数p/Fa和β/Fr进行模拟的,但是由于纵向无直接升力控制能力,不能改变飞机的升力线斜率,因此只能对q/Fe进行模拟。要想模拟等效传递函数nz/q和 nz/α,必须增加对和速度 V的模拟,而要实现升力线斜率的模拟,可以借助于对迎角或航迹角的模拟,这样就要求除升降舵外还应有直接升力面和发动机油门的控制。
因此,本文中多自由度变稳选取的主跟踪变量纵向为俯仰角速率、迎角和速度,主控制舵面为升降舵、直接升力襟翼和发动机油门;而横航向与三自由度变稳相比,并没有太大变化,仍然为滚转角速度和侧滑角,主控制舵面为副翼和方向舵。
2 基于自适应的多自由度变稳控制律
2.1 自适应控制策略
根据空中飞行模拟的特点,同时为了保证自适应模型跟踪的性能,本文采用参数自校正自适应控制方法,其结构框图如图1所示[2]。从图1中可以看出,用于多自由度变稳的参数自校正自适应控制主要包括内环和外环两个部分,内环包括了基本的模型跟踪回路和自适应控制律,外环主要是参数估计和控制器设计两个部分。
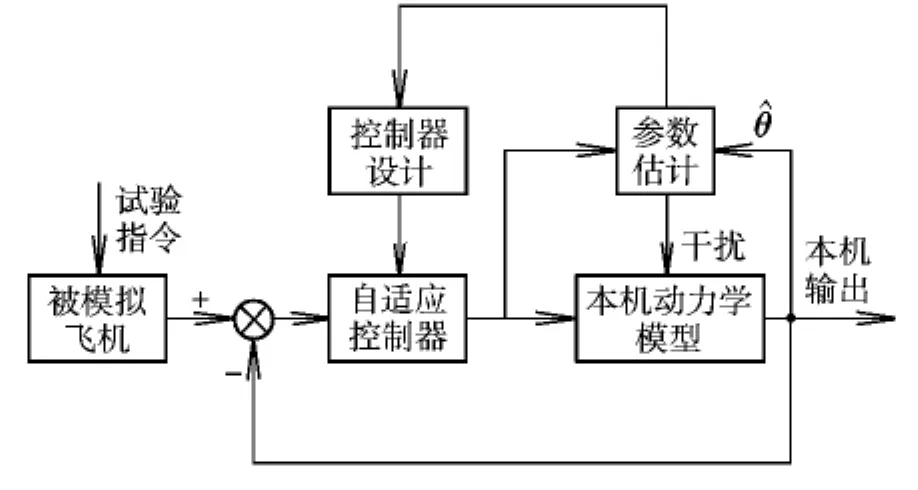
图1 参数自校正自适应控制Fig.1 Parameter self-tuning and self-adaptive control
2.2 基于自适应的多自由度变稳控制律
本机运动由如下状态方程表示:
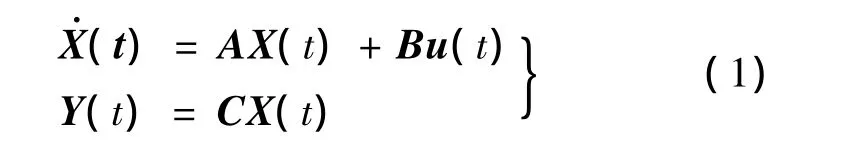
假定本机为“正常”的,即矩阵C和B的乘积CB为满秩矩阵,这时控制律为离散形式的PI输出反馈控制律[3]:

式中:k为整数;T为采样周期;Kp,KI为控制律增益矩阵;e(kT)为kT时刻模型飞机和本机输出响应误差;z(kT)为误差向量的数值积分。显然,该控制律的关键在于如何确定控制增益矩阵Kp和KI。
引入系统的采样阶跃响应矩阵:
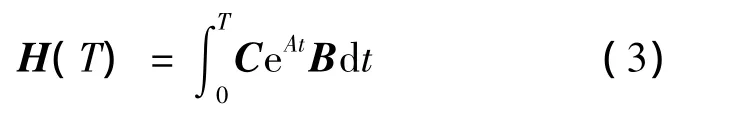
将式(1)描述的本机连续状态空间模型离散化,在相同的输入及初始条件下,忽略零均值的方程误差,经过推导可得:
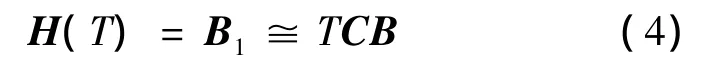
式中:B1为本机状态方程离散化后的系数。
这样,式(2)表示的离散形式的PI控制律增益可以表示为:
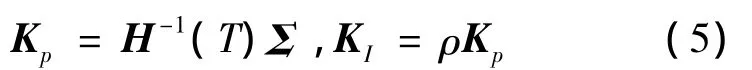
式中:Σ =Diag(σ1,σ2)为对角矩阵;ρ为大于零的实数。
这样,根据本机输入-输出数据就可以实时地估计出B1阵的各元素,从而确定出更新的阶跃响应矩阵,进而根据式(2)和式(5)产生新的自适应控制律,从而获得反映飞机当前运动的特性。
由于对油门的控制牵涉到对发动机的控制,因此本文中对速度的跟踪即自动油门回路仍然采用经典的PID控制律。这样,纵向和横航向自适应控制律在结构及设计过程并没有多少差别,无论是纵向还是横航向所需估计的矩阵B1均为2×2的矩阵。
2.3 改进的递推最小二乘参数估计算法
由图1可知,参数估计是参数自校正自适应控制很重要的一个方面,由于现代飞机参数变化范围很大,同时考虑实时在线参数估计的需要,本文采用递推最小二乘估计方法,结合空中飞行模拟的特点对该算法进行了如下改进:即引入“参数失调检测”算法和“噪声方差估计器”用以提高参数估计算法的收敛性和算法的鲁棒性[4]。
上述改进的递推最小二乘估计算法在MATLAB中的运行流程如图2所示。
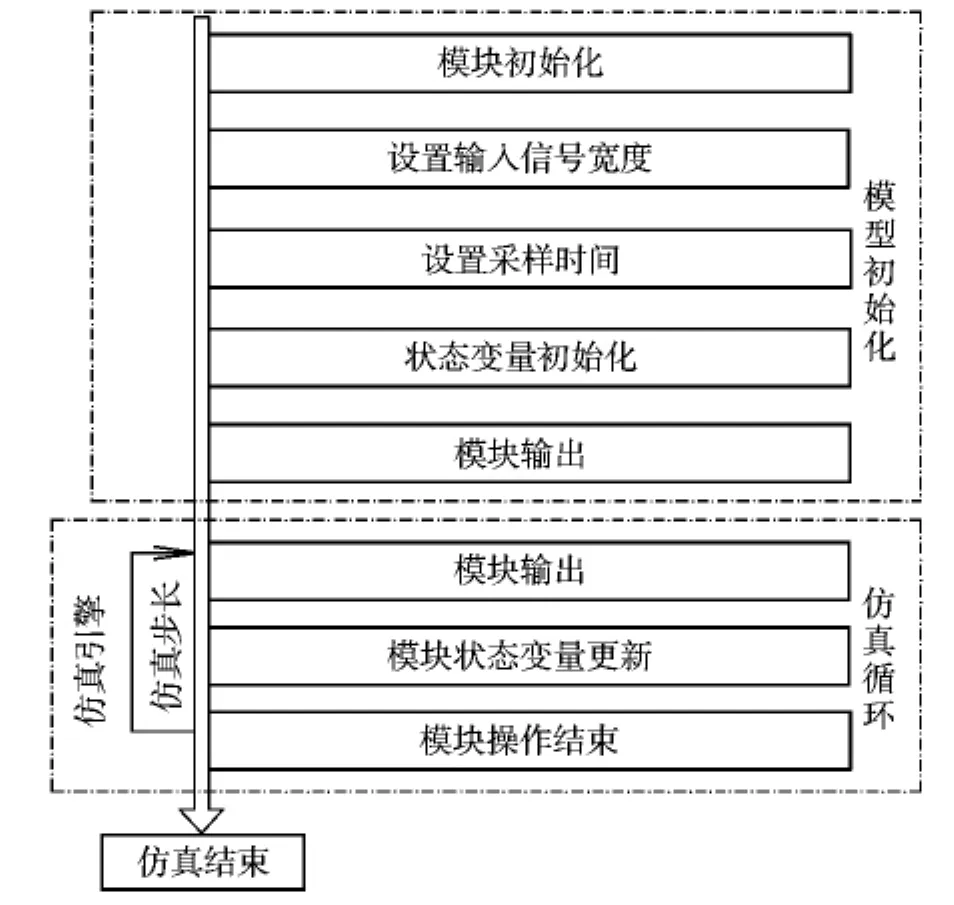
图2 改进的递推最小二乘估计算法流程Fig.2 Flow diagram of improved RLSalgorithm
3 数值仿真结果与分析
为了验证上述自适应控制策略的有效性和算法的正确性,在MATLAB环境下建立了多自由度变稳自适应控制模型。建模过程中,模型飞机采用小扰动状态方程模型,选取如下状态点:H=500 m,Ma=0.27,着陆构型;本机采用六自由度全量运动方程模型,在以下状态点进行配平:H=1 000 m,Ma=0.23,着陆构型。
由于纵向和横航向控制律结构和建模过程比较相似,因此本文重点以纵向为例进行仿真建模与分析,建模内容主要包括模型飞机模型、参数估计模型、自适应控制律模型和本机模型等。参数估计的目的是根据输入输出数据得到控制律参数调整所需的阶跃响应矩阵H(T),然后根据自适应控制律表达式(2)和式(5)得到本机所需的控制舵面输入。
从自适应控制律表达式可以看出,该控制律参数主要包括对角矩阵Σ的两个元素σ1,σ2和大于零的调节系数ρ。为了分析控制律参数对跟踪性能的影响,采用固定3个参数σ1,σ2和ρ中的两个来考核纵向阶跃输入信号作用下航迹角和俯仰角速率的跟踪响应情况,仿真结果如图3~图5所示,最终确定的纵向控制律参数为Σ =Diag(0.6,0.7),ρ=0.8。
从仿真结果及参数调整过程可以看出,控制律参数的选取应首先保证飞机的稳定性,对角矩阵Σ用以调整飞机的瞬态响应。对纵向而言,Σ中的元素主要影响航迹角和俯仰角速率的模拟,而常数ρ主要用于调节瞬态响应的误差。
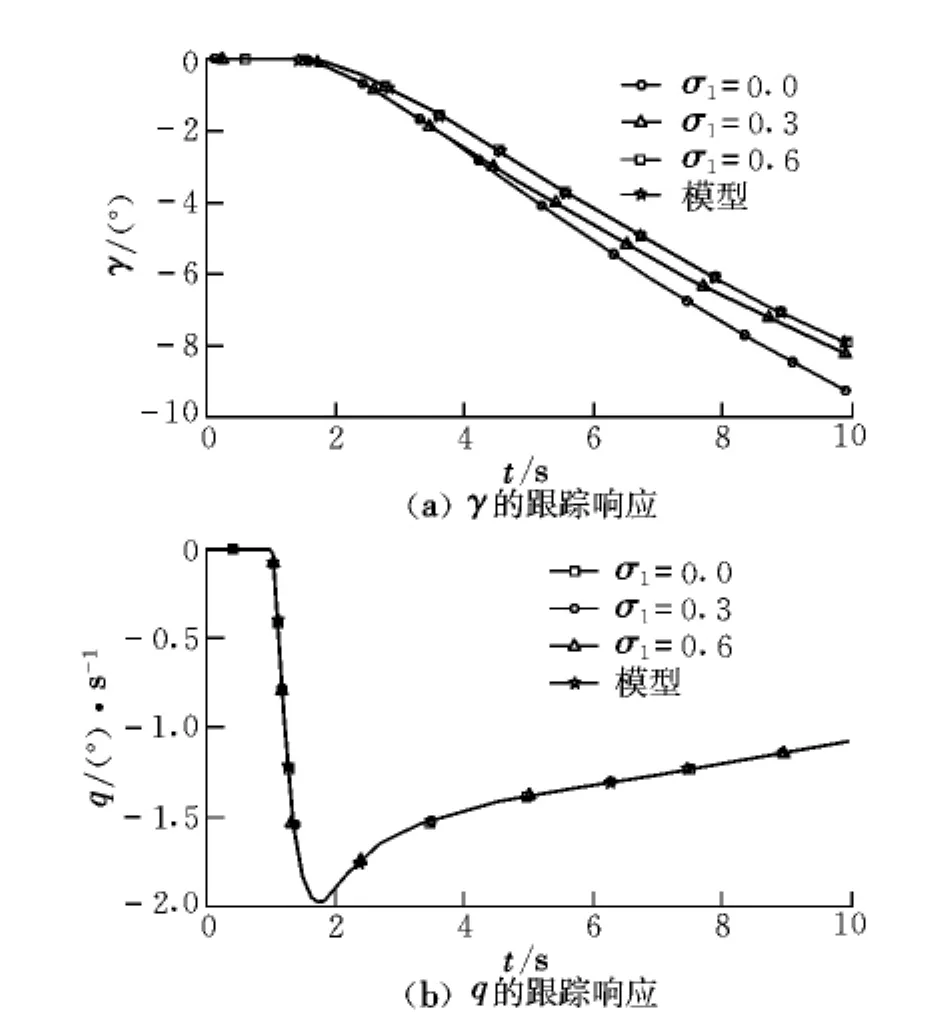
图3 σ1变化时γ和q的跟踪响应(σ2=0.7,ρ=0.8)Fig.3 Flowing response ofγand q withσ1 changed(σ2=0.7,ρ=0.8)
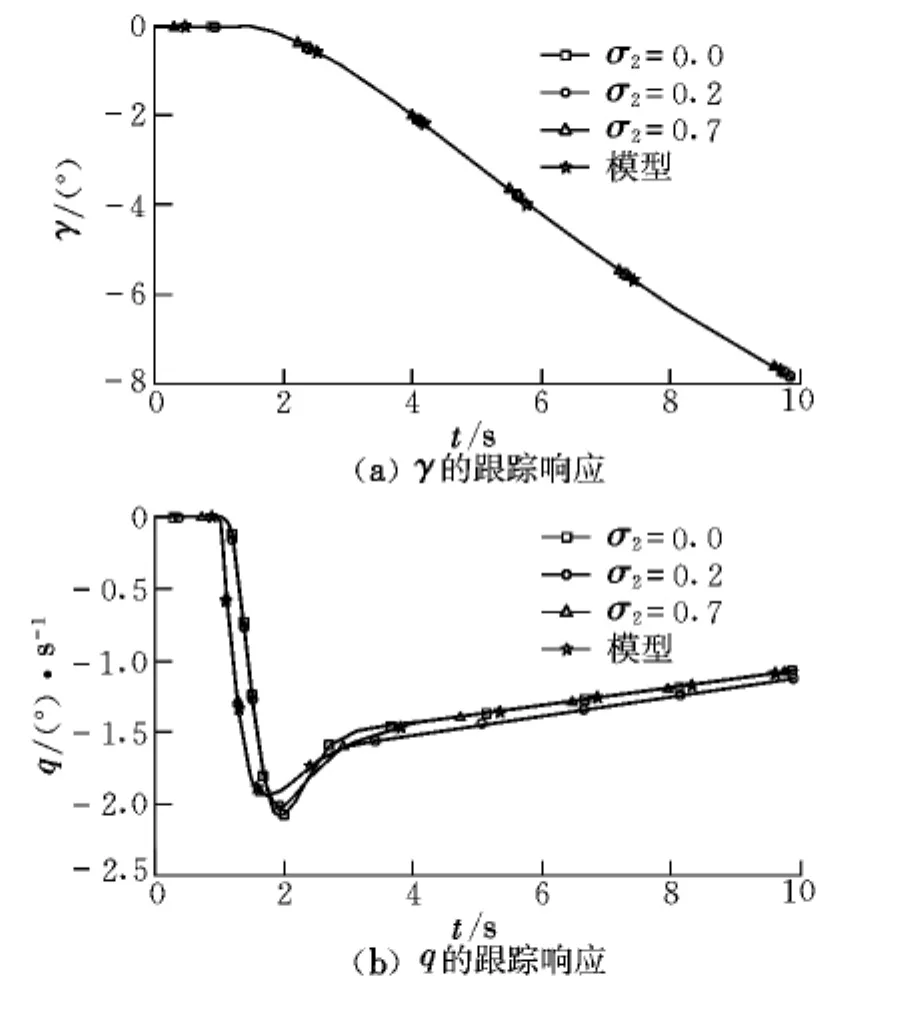
图4 σ2变化时γ和q的跟踪响应(σ1=0.6,ρ=0.8)Fig.4 Following response ofγand q withσ2 changed(σ1=0.6,ρ=0.8)
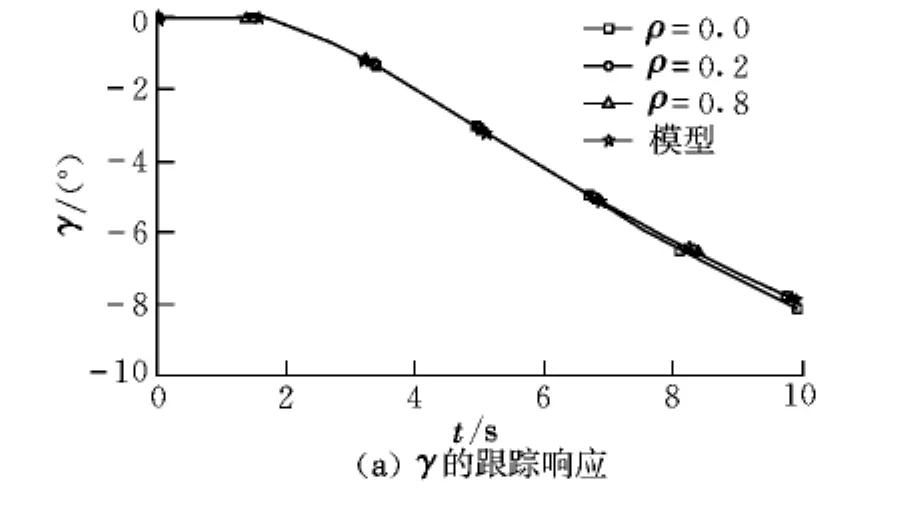
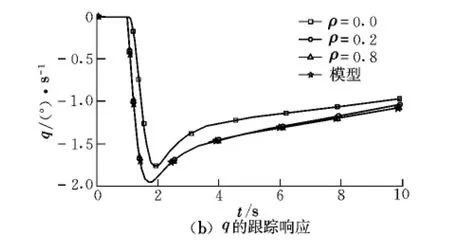
图5 ρ变化时γ和q的跟踪响应(σ1=0.6,σ2=0.7)Fig.5 Following response ofγand q withρchanged(σ1=0.6,σ2=0.7)
与三自由度变稳相比,多自由度变稳主要区别在于纵向增加了直接升力控制舵面。根据前面的分析,增加直接升力控制后可以对迎角和航迹角进行精确跟踪模拟。在相同的初始状态和阶跃输入信号作用下,两者纵向跟踪响应结果如图6所示。从仿真结果可以看出,多自由度变稳对于迎角和航迹角的模拟要明显优于三自由度变稳的模拟。
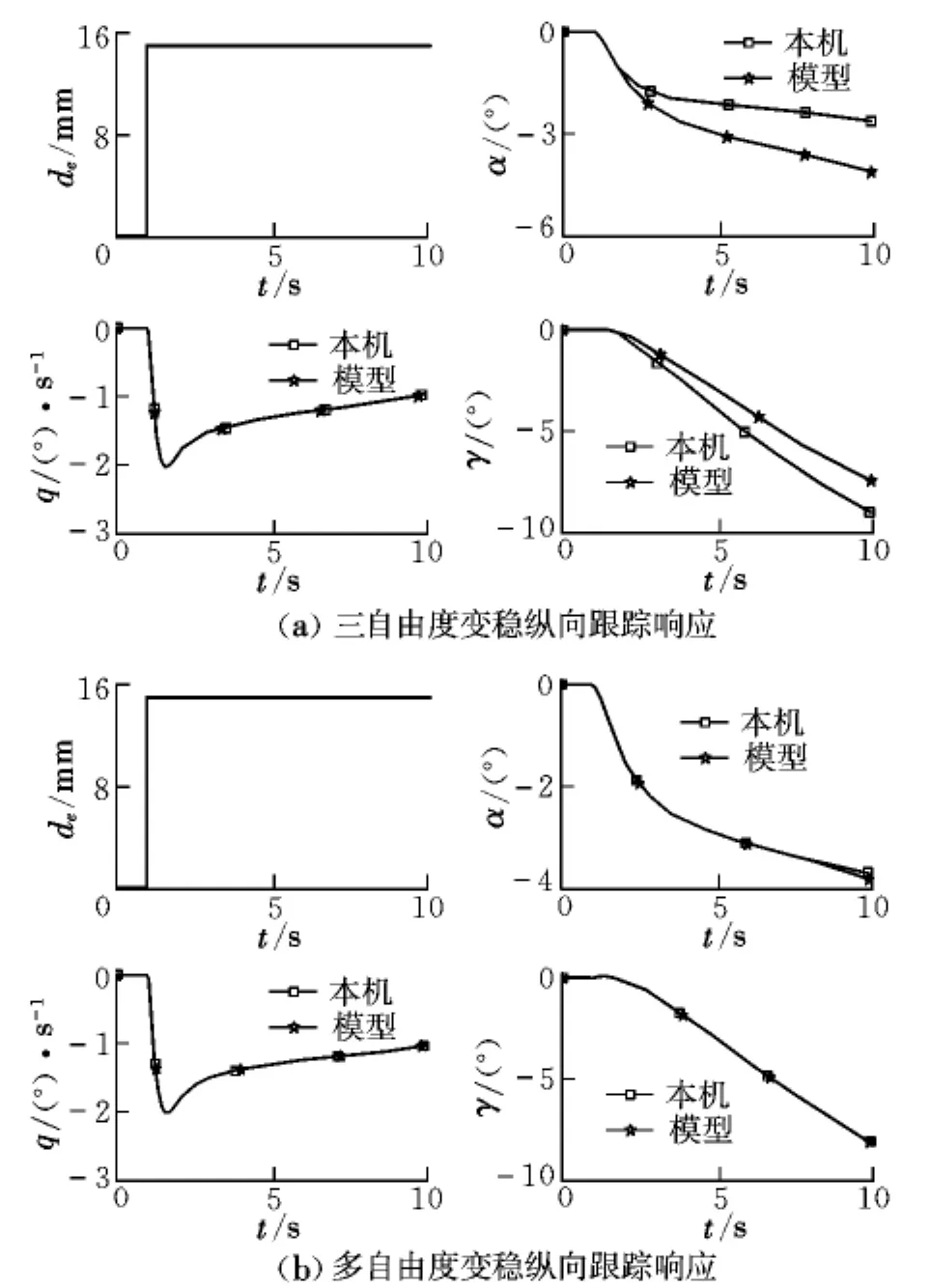
图6 纵向跟踪响应的对比Fig.6 Comparison of longitudinal following response
4 半物理仿真
为了进一步验证所采用的自适应控制方法的有效性和控制律的鲁棒性,本文在半物理仿真试验台上进行了仿真试验。半物理试验台环境包含有真实的物理舵机和数字式可变人感系统,同时采用电动加载系统模拟作用在舵机上的气动力和力矩。
试验内容包括稳定裕度测试和控制律的鲁棒性测试。稳定裕度测试即在舵机输入前端给飞控系统加入正弦扫频激励信号,利用快速傅立叶变换(FFT)得到飞控系统的稳定裕度[5];鲁棒性测试方法即在相同的初始状态下,偏离配平点高度±500 m范围内施加正反方向阶跃信号,得到经典和自适应两种控制律下的飞机响应的时间历程曲线。
半物理试验台环境下的稳定裕度试验结果如表1所示,鲁棒性测试结果如图7所示。从表1和图7可以看出,采用自适应控制律设计的多自由度变稳控制律能够满足幅值裕度大于6 dB、相位裕度大于45°[6]的稳定性要求,并且对选取的主变量有较满意的跟踪性能,同时与经典控制律相比该控制方法也具有一定的鲁棒性。

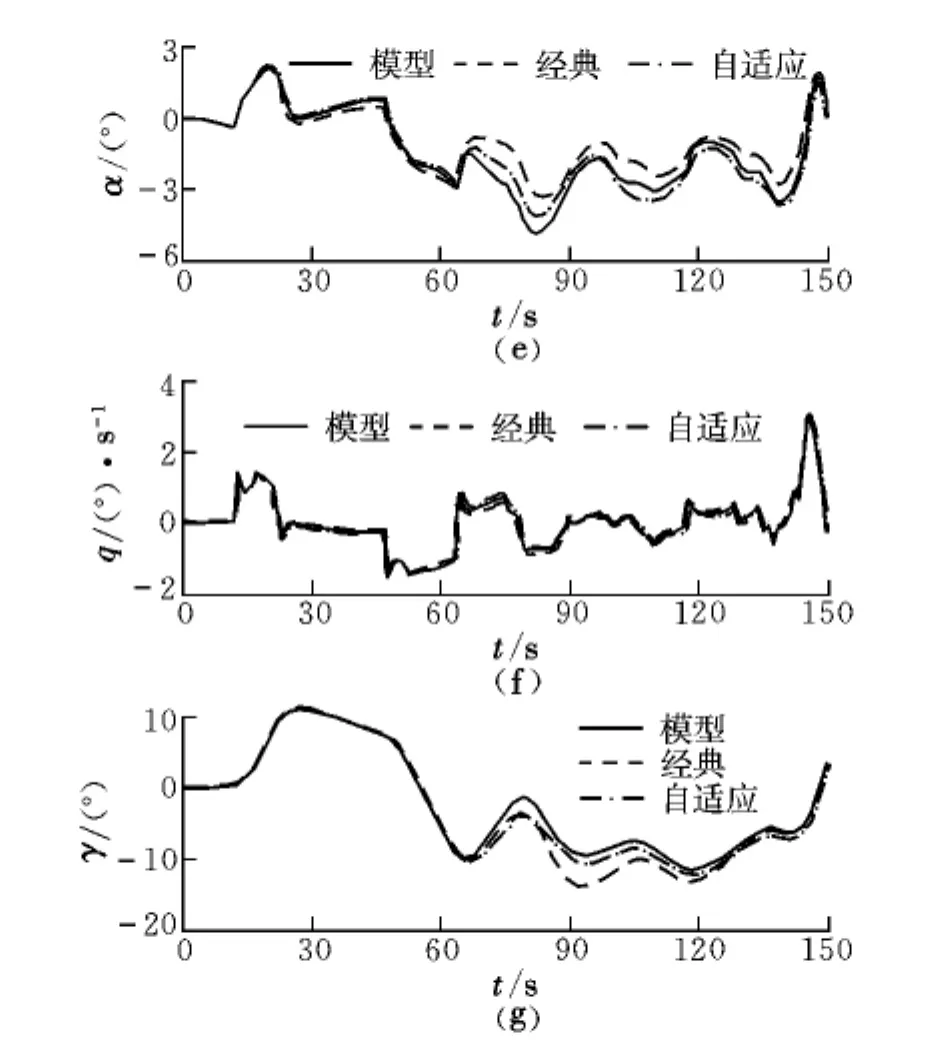
图7 鲁棒性试验结果Fig.7 Test results of robustness
5 结束语
本文根据空中飞行模拟器的特点和使用要求,采用参数自校正自适应控制策略,在固定增益控制律的基础上,基于输出反馈理论形成了自适应控制律,并对自适应所需的辨识算法进行了改进,最终形成了自适应控制所需的辨识算法流程。MATLAB数值仿真和半物理仿真试验结果表明,加入直接升力控制后能显著提高对迎角和航迹角的跟踪模拟,该控制方法满足稳定性和控制律鲁棒性的要求。同时采用自适应控制技术能够减少调参工作量,降低对本机稳定性导数的依赖。此外,需要指出的是,直接升力面对迎角和航迹角的跟踪影响较大,在以后的研究中需要着重考虑直接升力面的变稳能力。
[1] 刘兴堂,吕杰,周自全.空中飞行模拟器[M].北京:国防工业出版社,2003:29-55.
[2] 刘兴堂.现代辨识工程[M].北京:国防工业出版社,2006:243.
[3] 刘兴堂.应用自适应控制[M].西安:西北工业大学出版社,2003:458-469.
[4] Luis A Pineiro.Parameter-adaptive model-following for inflight simulation[D].AD-A190567,1987.
[5] 李建平.飞控系统稳定裕度试飞技术[C]//控制与应用第九届学术年会.成都:中国航空学会,2000:194.
[6] Katsuhiko Ogata.现代控制工程[M].卢伯英,佟明安,译.北京:电子工业出版社,2011:354.
