一般斜入射情形下平面透射光栅衍射现象分析

张明霞，赵玉祥

（天水师范学院 电子信息与电气工程学院，甘肃 天水 741001）

目前国内常见《光学》教材[1-9]的相关章节中仅仅介绍了平面光波在垂直入射或其中一种特殊斜入射于平面透射光栅（以后简称光栅）时的光栅方程，利用此光栅方程分析衍射图样分布特征.但在分光计上做光栅衍射实验时发现，由于光源为缝光源，平行光管出射的平面光波包含了多种入射方式（包括特殊入射及一般斜入射），实验中产生的衍射图样随着平面光波入射方式的不同而产生复杂的变化，利用垂直入射或特殊斜入射时的光栅方程不能完全解释光栅衍射实验现象，使得长期以来的光栅衍射实验教学存在着用特殊指导一般、个别演示普通的状况，从而在光栅衍射理论和实验教学中形成了令学习者困惑生疑的模糊地带.下面，笔者拟从几何成像的角度，结合光栅衍射理论，分析光源和衍射图样之间的关系，得到平面光波在一般斜入射于光栅时的衍射图样分布特征，完全解释光栅衍射实验现象.

1 光栅衍射实验装置示意图

图1所示为常规在分光计上做光栅衍射实验时的简单装置示意图.[10-11]高压汞灯发出的光波（复色光）先经过平行光管，平行光管的左端有一狭缝S，可看作一缝光源，缝光源S位于平行光管的物方焦面上，平行光管后依次是光栅及望远镜，通过望远镜观察光栅衍射图样.为了方便讨论，建立如图所示的坐标系.国内常见《光学》教材中S为点光源（位于焦点），当S为点光源时，平面光波垂直入射于光栅平面，而常规的光栅衍射实验中，S为缝光源时，平面光波包含了多种入射方式（取决于狭缝的方向），两种实验装置中光源不同，平面光波的入射方式不同，因而产生的衍射图样不同.

图1 光栅衍射实验装置示意图

2 光栅衍射实验现象

图2、图3、图4分别为缝光源在不同方向时的光谱线（即衍射图样），设缝光源与y轴之间的夹角为φ'.图2为缝光源伸展方向与光栅狭缝伸展方向平行时的光谱线，光谱线和Y轴平行，并且和Y轴呈对称分布，中央谱线最亮；图3为缝光源伸展方向与光栅狭缝伸展方向垂直时的衍射图样，此时光谱线在x方向压成一条强度连续变化的亮线，中央有一个很大的区域，很亮，呈白色，两端光的强度逐渐减弱，最外端呈现紫色，并且相对原点O对称分布；图4为缝光源伸展方向与光栅狭缝伸展方向成任意角度φ'时的光谱线，光谱线与y轴之间夹角仍为φ'，同一级谱线从中央亮纹依次向外分别为紫线、绿线、黄线，最后一级谱线中只能观察到紫色的谱线.

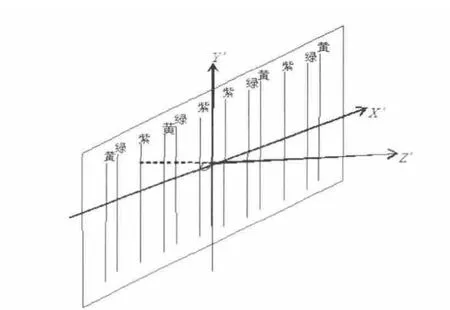
图2 缝光源伸展方向与Y轴平行时的衍射图样

当S为点光源时，衍射图样为亮暗相间的衍射斑，[1-9]用点光源的衍射图样不能解释缝光源的衍射图样.下面，笔者先从几何成像的角度，结合衍射理论，分析点光源和衍射图样的关系，再定性分析光源为缝光源时的衍射图样，最后解释常规的光栅衍射实验现象.

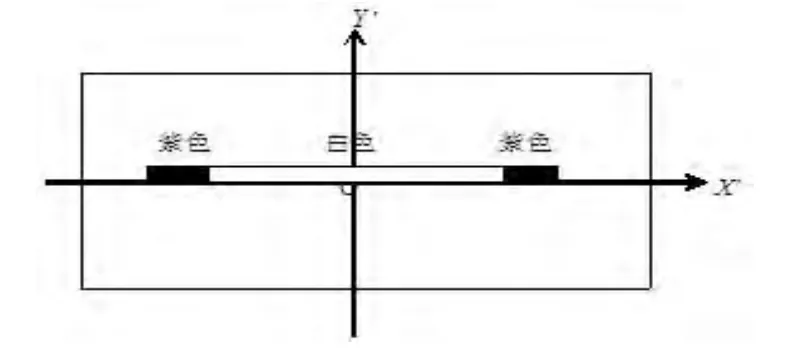
图3 缝光源伸展方向与Y轴垂直时的衍射图样

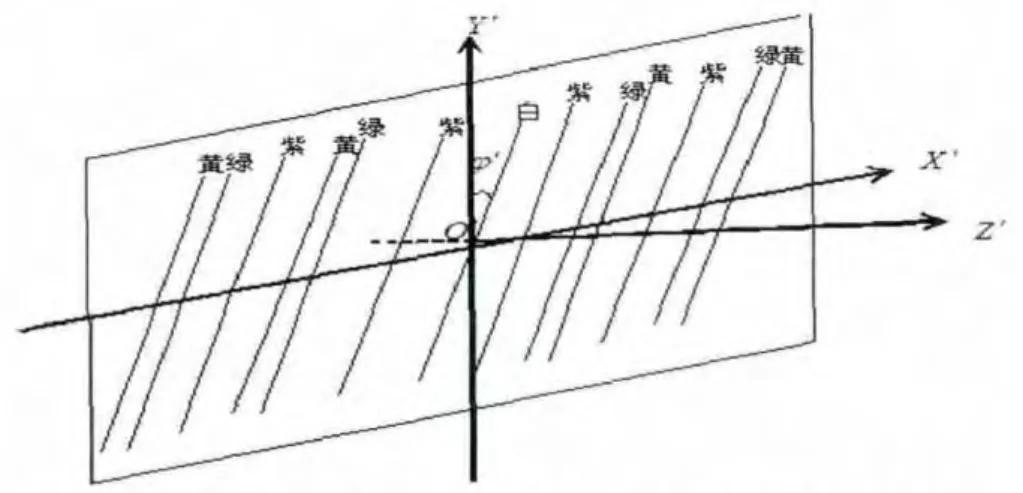
图4 缝光源伸展方向与Y轴成夹角φ′时的衍射图样

3 光源为点光源时的衍射图样分析

为了研究点光源和衍射图样之间的关系，实验采用激光（以方便改变平面光波的入射方位）直接照射光栅，将平面光波的入射方式改变为一般斜入射，相当于点光源在平行光管焦平面上任意方向移动.

图5为激光束垂直入射于光栅平面时的衍射图样，此时衍射图样为中央有一强度很大的衍射斑，其他衍射斑相对于中央衍射斑对称分布，且各级衍射斑分布在与x轴平行的直线上.

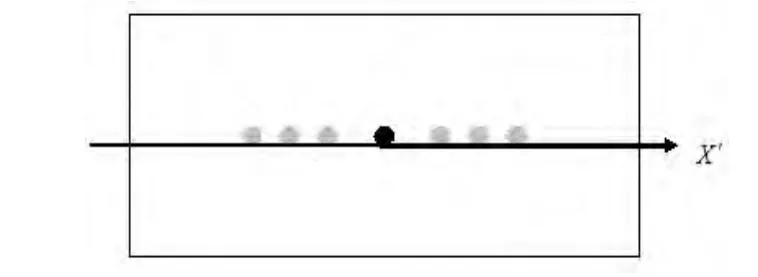
图5 激光与光栅平面垂直时的衍射图样

图6是激光束方向与XOZ平面平行时的衍射图样，这种入射方式是特殊斜入射，此时衍射图样为中央仍有一强度很大的衍射斑，其他衍射斑相对于中央衍射斑呈不对称分布，但各级衍射斑仍分布在与x轴平行的直线上.

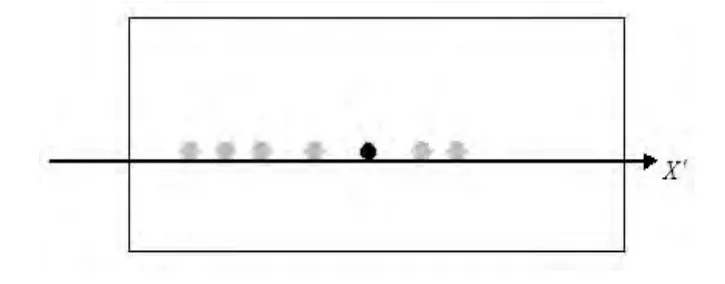
图6 入射光线平行于XOZ平面时的衍射图样

图7是激光束方向与YOZ平面平行时的衍射图样，这种入射方式是仍然是特殊斜入射，入射光线与X轴间夹角为γ，γ=90°，各衍射斑呈对称分布，中央衍射斑在Y轴上，其他各级衍射斑分布在x轴上方或下方的一条直线上，并与X轴平行.

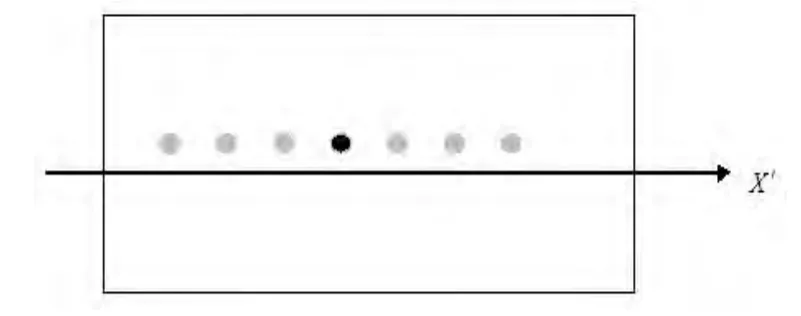
图7 入射光线平行于YOZ平面时的衍射图样

图8是激光束在任意方向斜入射于光栅平面时的衍射图样，任意斜入射就是指这种情行，衍射图样呈现不对称分布，中央衍射斑离开Y轴，其他各级衍射斑分布在x轴上方或下方的一条直线上，但与X轴不平行.

图8 入射光线任意斜入射于XOY平面时的衍射图样

利用常见《光学》教材中介绍的垂直入射及特殊斜入射时的光栅方程可以分析图5和图7中衍射斑的分布特征，但由于图6中平面光波的入射方式为另一种特殊斜入射，图8中平面光波的入射方式为任意斜入射，因此，常见《光学》教材中介绍的垂直入射及一种特殊斜入射时的光栅方程无法分析图7和图8中衍射斑的分布特征.

综上可知，不管激光是垂直入射、特殊斜入射，还是一般斜入射，当光源为点光源时，衍射图样的零级衍射斑（最亮）总是出现在不考虑衍射时点光源几何像点的位置，其他各级衍射斑在零级衍射斑两侧展开且分布在某一平面（和入射方式有关）内，由几何光学成像的角度看，当点光源在平行光管焦平面内任意移动时，几何像点的位置随着点光源位置的变化而变化，相应的衍射图样所在的平面也发生了改变.当光源为缝光源时，衍射图样可看作是每一个点光源所产生的衍射图样非相干叠加的结果，所以，点光源和衍射图样间的关系对缝光源同样适用.

4 光栅衍射实验现象分析

缝光源S可以看作是无穷多个点光源的集合，因此，每一个点光源经过平行光管后，以不同的方位入射于光栅平面，在分光计上做光栅衍射实验时，衍射图样可看作是每一个点光源所产生的衍射图样非相干叠加的结果，由于汞灯是复色光，衍射图样中出现了彩色的光谱线.下面具体分析常规衍射实验中光源为缝光源时的衍射图样.

4.1 缝光源和y轴平行时的衍射图样

如图1所示，当缝光源和Y轴平行时，所有平面光波垂直入射于光栅平面或平面光波的方向平行于YOZ平面（另一种特殊斜入射）.由图5可知，狭缝光源上的每一个点光源产生的衍射图样均沿X方向伸展，即当光源为缝光源时，衍射图样的零级主极大和Y轴重合，由几何光学成像理论可知，当狭缝光源和Y轴平行时缝光源所成的像就和Y轴重合.因此，在光栅衍射实验中，缝光源经过光学系统所成的像在什么位置，衍射图样的零级主极大就出现在什么位置，其他各极主极大对称的分布在两侧，每一个点光源所产生的衍射图样非相干叠加的结果得到如图2所示的彩色衍射图样.

4.2 缝光源与y轴垂直时的衍射图样

当缝光源和Y轴垂直时，所有平面光波方向平行于XOZ平面.在这种特殊斜入射情形下，由图6知，缝光源上的每一个点光源产生的衍射图样均沿X方向伸展，零级主极大分布在X轴上；又由前面分析可知，零级主极大出现在像的位置.因此，由几何成像的观点可知，各点光源对应的像点错开排列在X轴上，由于点光源是连续分布的，每个点光源产生的衍射图样非相干叠加的结果，出现了如图6所示的衍射图样，零级主极大（即像点）宽度加宽且仅在x方向，缝光源越长，谱线越宽，并且多级光谱线重叠在一起，在中央零级亮纹强度最大，两侧强度逐渐减弱，并且两端出现很明显的紫光，这是因为在各级光谱中，随着级数的增大，谱线强度逐渐减弱，多级光谱重叠的结果是两侧出现紫色.

4.3 缝光源与y轴的夹角为任意角度时的衍射图样

当缝光源与y轴的夹角为任意角度时，每一个点光源对应的平面平面光波任意斜入射于光栅平面，但是，根据几何成像理论及衍射理论，不难得到零级主极大仍在缝光源的像的位置.缝光源以z为轴旋转一周，则狭缝像在XOY平面内旋转一周，则各谱线也在XOY平面内旋转一周.如图4所示，反过来若保持缝光源的位置不变，将光栅以z为轴旋转一周，谱线方向不变，因为狭缝光源的方向没有变化，但是各级谱线的位置在x方向发生变化，当变到90°时，所有谱线都重叠在一起，此时平面光波的方向平行于XOZ平面，满足特殊斜入射条件，每个点光源产生的衍射图样非相干叠加的结果，出现了如图3所示的衍射图样.

从以上分析可知，由几何光学的成像理论，在不考虑衍射的情况下，光源是什么形状，在观察屏上得到的像应该就是什么形状；又依据衍射理论，衍射图样中央主极大就是在不考虑衍射的情况下几何像的位置，其他各级主极大分布在中央零级主极大两侧，因此，从几何成像的角度，结合衍射理论，就可以定性分析衍射图样分布特征，解释光栅衍射实验现象.

5 结 语

因为常见《光学》教材[1-9]中的相关平面光波垂直入射及特殊斜入射光栅方程不能解释光源为缝光源时的衍射图样，笔者从几何光学成像的角度，结合衍射理论分析了光源为点光源或缝光源的衍射图样.不管平面光波是垂直入射、特殊斜入射，还是一般斜入射，衍射图样的零级衍射条纹（最亮）总是出现在不考虑衍射时光源几何像点的位置，其他各级衍射斑在零级衍射斑两侧展开且分布在某一特殊平面（和入射方式有关）内，每一个点光源所产生的衍射图样非相干叠加的结果，得到了如图2、图3、图4所示的衍射图样，完全解释了光栅衍射实验现象.这种解释是对常见《光学》理论和实验教材中光栅衍射理论的更进一步拓展和完善.

[1] 蔡履中.光学[M].北京：科学出版社，2007：242-246.

[2] 赵凯华，钟锡华.光学：上[M].北京：北京大学出版社，1999.

[3] 赵凯华，钟锡华.光学：下[M].北京：北京大学出版社，1999.

[4]E.HECHT，AZAJAC.光学：下册[M].詹达山，等，译.北京：人民教育出版社，1980.

[5] 牟绪成，邓新元，董文达.波动与光学：下册[M].北京：清华大学出版社，1994.

[6]张三慧.波动与光学[M].北京：清华大学出版社，2000.

[7]姚启钧.光学教程[M].北京：高等教育出版社，2003.

[8]钟锡华.现代光学基础[M].北京：北京大学出版社，2003.

[9]MAX BORN，EMIL WOLF.Principle of Optics M.Six(corrected)edition[M].London：CambridgeUniversityPress，1997：385.

[10]杨述武，王定义.普通物理实验：三·光学部分[M].北京：高等教育出版社，2002.

[11]张兆奎.大学物理实验[M].北京：高等教育出版社，2001.