中国工业部门产能过剩的测度与影响因素分析

杨振兵 张 诚

一、引 言

改革开放以来，在经历了持续高速的经济增长之后，产能过剩问题日益突显。工信部原部长李毅中指出：“按照世界公认的标准，利用率小于75%,就是严重过剩，中国39 个行业中有21 个都属于产能严重过剩。”产能过剩引发市场恶性竞争、经济效益难以提高、企业倒闭或开工不足、人员下岗失业、银行不良资产等一系列问题，会严重影响经济发展的质量。2014 年中央经济工作会议也提出：坚定不移化解产能过剩，不折不扣执行好中央化解产能过剩的决策部署。

学术界对于产能利用率的关注远远高于产能过剩(钟春平和潘黎，2014)，而且对于产能过剩的定义仍然存有争议。Chamberlin(1947)率先提出产能过剩的定义，并认为是由不完全竞争的组织无效率引起的。Kamien 和 Schwartz(1972)指出产能过剩是垄断竞争企业平均成本最小时最优产出大于实际产出的情形。但在实际运用时，往往将产能过剩理解为市场需求小于实际产出水平即“供过于求”的状态。因此产能过剩问题不仅体现在生产能力的过剩，还体现在购买力不足、需求不景气时出现的产能过剩。因此，产能过剩事实上受到经济周期、可支配收入(包括个人与企业)甚至是偏好、风俗习惯等因素影响。

关于“产能利用率”，Berndt 和Morrison(1981)认为，就是实际产出与潜在产出的比值，其中潜在产出是基于之前的产出-资本比的峰值和累计净投资计算的；王维国和袁捷敏(2012)也用这种方法对产能利用率进行了测算，但是只考虑资本投入，忽视了其他生产要素的决定性作用。类似地，其他一些具有代表性的研究分别采用不同方法对资本设备利用率进行估算(龚刚和杨琳，2002；何彬，2008；杨光，2012)，同样只考虑资本的利用率，忽视了劳动投入这一重要的生产要素，更没有考虑生产过程中不同要素的替代弹性。基于多要素投入对产能利用率的估算，大致可以分为生产法与成本法。其中成本函数法能够综合考虑生产过程中的各种要素投入，同时利用要素投入价格可以计算出生产成本的价值量，因而被广泛运用(Morrison，1985；Berndt 和 Fuss，1989；Nelson，1989；Segerson 和 Squires，1990；孙巍等，2009；韩国高等，2011)。但由于成本核算难度大、数据信息的获得性低(尤其是生产要素的价格等)，依据产能过剩的概念从成本的角度来测度是非常困难的，甚至有学者认为用成本判定产能过剩本身就存在缺陷(Demsetz，1959；Klein，1960)。

为了较好的规避价格与成本等因素导致的测算误差，数据包络分析(DEA)与基于超越对数生产函数的随机前沿分析(SFA)提供了较为便捷的计算方法。其中数据包络分析(DEA)利用了动态规划的思想，不必设定具体的生产函数，也不涉及价格因素，只需考虑生产要素投入数量，衡量现实产出相对于潜在产出的效率而被应用(Kirkley 和Squires，1999；Dupont 等，2002；Sahoo 和Tone，2009)，但可惜的是这种方法也没有考虑不同生产要素间的替代弹性，而且衡量潜在产出的生产前沿是固定的，对于不同时期不同行业的跨期面板数据而言脱离现实。随机前沿分析(SFA)恰好避免了这个缺陷，它不仅充分考虑了不同生产要素的替代弹性，而且测度潜在产出的生产前沿是随机的，这就更加符合现实，不仅如此，还可以通过设定具体的生产函数而检验各个参数与模型本身设定的合理性。Kirkley 等(2002)分别用DEA 与SFA 两种方法对产能利用率进行了测算与比较。

本文在借鉴Kirkley 等(2002)方法基础上，测算了生产环节的产能利用率，并根据供需不平衡的现实特征，利用市场需求-供给比率对其进行修正，以准确识别与分析产能过剩的成因，为解决产能过剩问题提供必要的经验支持。本文后续部分将做如下安排：第二部分采用基于规避价格因素的超越对数生产函数的随机前沿模型计算生产环节的产能利用率，并用市场需求-供给比率进行修正计算得到实际的产能过剩指数；第三部分建立动态面板模型，采用能够有效控制内生性的系统广义矩估计考察了投资比重、劳动投入、外资比重、行业竞争强度、创新投入等因素对产能过剩的影响；第四部分为结论与政策含义。

二、中国工业行业产能过剩指数测算

（一）产能过剩的重新定义

学术界与现实意义上的产能过剩并不完全相同，现实意义层面上是指实际生产产量超过市场总需求，然而总需求由消费能力决定，更深层次上由经济周期、可支配收入、偏好以及风俗习惯等因素决定。学术意义上的产能过剩是指工业企业实际生产产量低于潜在生产能力的现象(Kamien 和 Schwartz，1972；Kirkley 等，2002)，由于生产过程中往往存在技术效率的损失(后文简称“技术无效”)，实际产量通常要低于所能够达到的潜在生产能力(即产能利用率小于1)，因此产能过剩现象普遍存在。为了更为清楚理解产能过剩，我们需要厘清以下几个概念。

潜在生产能力(YP)，在当前的技术、管理能力条件下充分利用可得生产要素所能达到的最优产出，是理想化的目标产出。

实际生产产量(Y)，即利用现有的生产要素在现实条件下生产的实际产出。

市场需求水平(YD)，是指市场所能消化的工业生产产量，也就是现实情况下的行业销售产值。

潜在市场需求水平(YT)，是指在市场有效之时，也就是充分竞争的情况下，市场所需要商品的数量，也可以理解为长期内利润为零之时厂商的供给数量。

通常情况下 YD＜ YT，这是由于市场分割、商品价格扭曲、产品质量差异化等原因所致。由于生产过程中技术无效的存在，通常而言使得 Y ＜ YP，技术无效主要体现在管理经验不足、技术使用不充分而不可避免地导致生产要素的投入结构非最优配置等。

所以明显地，采用成本法测算的产能利用率(如韩国高等，2011)是实际生产产量(Y)与潜在市场需求水平(YT)的比值，而由于成本核算受数据(尤其是价格)准确性影响较大，所以测得的产能利用率通常具有较大误差(Demsetz，1959)，而且忽视了技术无效导致的潜在生产能力损失问题，这就意味着那些产能过剩的行业生产要素结构优化时产出增加供大于求的现象比测算结果更为严重；而生产法测得的产能利用率是实际生产产量(Y)在相比潜在生产能力(YP)条件下的生产效率，虽然将潜在生产能力(YP)纳入参考范畴，但是忽略了现实意义上市场需求因素对产能过剩的影响。因此，考虑到现有研究的不足，以及可观的可得数据的限制，本文参考Kirkley 等(2002)采用可以完全规避价格量纲的生产法来测算产能利用率，并用需求供给比率进行修正。具体计算方法为：工业企业生产的产品需经历生产与销售两个环节。第一步为生产环节，我们首先按照Kirkley 等(2002)的方法计算生产环节产能利用率，即以潜在生产能力(YP)为参考标准的工业企业现有实际产出的生产能力利用率。第二步为销售环节，我们用“需求-供给比率”指标来对生产环节产能利用率进行修正，以此反映消费层面消费能力的变动对产能利用率的影响。由于现有资料无法提供各工业行业准确及完整的产品供给与需求数据，因而我们将当期的工业总产值视为市场供给的指代变量，销售产值视为市场需求的指代变量，而“需求-供给比率”为市场需求与现实产量的比值 SR = YD/Y，而且在本文的研究样本区间内，所有行业的 SR ＜ 1，即生产产量大于销售值①由于企业会持有部分产成品库存用来应对预料外的需求增加，也有可能是市场上出现供大于求的现象导致产成品库存增加，因此样本区间内“需求-供给比率”总是小于1，我们用此来指标反映消费层面消费能力的变动对产能过剩的影响。作者在此对审稿专家的意见表示感谢。。

（二）生产环节产能利用率的测算方法

基于Kirkley 等(2002)，我们将分别通过DEA与SFA两种不同方法测算产能利用率。

DEA 方法：Färe 等(1984)率先将DEA 引入产能利用率的测算，该方法通过假定一个固定的生产前沿(潜在产出能力)，然后利用线性规划的办法计算每个产出相对于该生产前沿的生产效率，也即产能利用率。其计算方法如下：

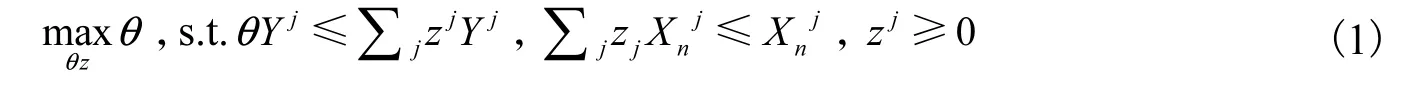
上式中，X 为生产投入向量，包括资本投入K 与劳动投入L，Y 为产出。

SFA 方法：根据Aigner 等(1977)及Meeusen 和van den Broeck(1977)分别独立提出了随机前沿分析方法，考虑到超越对数生产函数的要素产出弹性反映了投入要素之间的替代效应和交互作用，可以加入时间变化的影响而反映了不同投入技术进步的差异，同时也放宽了技术中性的强假设，能够揭示经济系统内的更多特征。此外，其形式较为灵活，可以有效避免由于函数误设而带来的偏差(涂正革和肖耿，2005；杨莉莉等，2014)。因此我们设定的生产函数的具体形式为：

其中，Y 为行业产出，i 为行业，t 为时间，K 为资本投入，L 为劳动力投入；v 为随机误差项，表示不可控的影响因素，作为具有随机性的系统非效率计算，且有；u 为技术损失误差项，用以计算技术非效率，且有；参数η 表示技术效率指数 uit的变化率。由于上述随机前沿模型的设定违反了最小二乘法(OLS)的经典假设，因此不能采用OLS 进行模型的参数估计。但根据Battese 和Coelli(1995)的研究，可以令γ 表示随机扰动项中技术无效所占的比重(如公式4)，利用极大似然法得到所有的估计量，同时还可以根据γ 的值判断方差中生产无效率方差所占的比重。γ 接近于1 时，则说明误差主要来源于u，即生产单位的实际产出与前沿产出之间的差距主要由技术无效所引起。因此，γ 的估计值还可以作为检验模型设定是否合理的一项依据。根据公式(5)，通过软件frontier 4.1 可以直接测出各年份不同行业在生产层面的产能利用率。

（三）数据来源

本文选取2001—2011 年中国工业36 个行业的面板数据作为研究样本，公式(1)中的投入产出数据来自《中国工业经济统计年鉴》、《中国劳动统计年鉴》等。含有价格因素的变量全部平减为2000 年不变价格序列。具体投入产出数据指标说明如下：

工业增加值(Y)：参考现有文献(涂正革和肖耿，2005；干春晖和郑若谷，2009)，我们采用不考虑中间产品投入价值的工业增加值作为产出指标，根据分行业工业品出厂价格指数对其进行平减至2000 年。其中由于《中国工业经济统计年鉴》中2008 年后不再提供工业增加值的行业数据，参考高越和李荣林(2011)、王兵等(2013)等现有研究的做法，根据中国统计局公布的历年年末工业分大类行业增加值增长速度与前一年的增加值数据计算得出。

工业资本投入(K)：不失一般性，采用资本存量进行度量。我们参考陈诗一(2011)的做法，按照永续盘存法，计算公式为：资本存量t=可比价全部口径投资额t+(1-折旧率t)×资本存量t-1，上式中的折旧率的计算公式为：折旧率t=(累计折旧t-累计折旧t-1)/固定资产原价t-1。显然，与大多数现有研究采用固定不变的折旧率相比，本文由统计数据推算得到的逐年变化的折旧率更加贴近现实情况，在此基础上估算得到的资本存量也应该更加准确。

工业劳动力投入(L)：采用各工业行业年均从业人数予以度量。

本文已将工业统计年鉴中36 个行业进行重新整理，由于统计口径不统一的原因，“其他采矿业”、“工艺品及其他制造业”、“废弃资源和废旧材料回收加工业”三个行业的数据没有包含在研究范围之内。为方便描述，所剩的36 个行业按照统计年鉴顺序依次标记为S1、S2、S3、……S36。

（四）生产环节产能利用率测算结果与比较

式(2)的参数估计结果如表1 所示。从模型参数来看，几乎所有的参数都是在1%,的水平上显著，说明模型中生产函数的变量设置较为合理。从模型整体的诊断性指标和生产无效率的检验来看，模型的极大似然估计值和单侧LR 检验值表明模型具有很强的解释能力。无效率项的均值 μ 为0.094,0，表明工业行业普遍存在生产无效率现象。总体方差，反映了生产波动情况，受到随机因素和无效率因素的影响，其值为0.242,3，表明误差项和无效率项虽然具有一定的波动幅度，但是并不大。值为0.993,5 且在1%,的水平上显著，说明组合误差项的变异来自于技术非效率，随机误差项带来的影响(0.65%,)微乎其微。因此，选用随机前沿模型比一般的模型能够更好地描绘各工业行业生产中的技术效率及其变化。

表1 超越对数生产函数参数估计结果

我们分别将DEA 与SFA 框架下对生产环节的年均产能利用率的测算结果报告于图1①限于篇幅，本文不再报告DEA 与SFA 框架下生产环节产能利用率的各年具体数据，有兴趣的读者可扫描本文二维码，查看本文附录。，可以清楚看出，除少数几个行业之外(S9、S11、S12)，几乎所有行业在SFA 的计算框架下产能利用率要明显地低于DEA 的计算结果，说明DEA 方法会高估生产环节的产能利用率，这是由于SFA 的计算方法充分考虑生产要素投入之间的替代弹性，而且潜在的生产能力是随着时间的推移而改变的(Kirkley 等，2002)。因此，为了更加准确的估计产能利用率，充分的考虑不同时期的潜在生产能力对产能过剩的影响，本文选择随机前沿分析方法来对中国工业行业的产能过剩指数进行测算。

图1 DEA与SFA框架下生产环节产能利用率比较

（五）考虑生产与需求的产能过剩指数

参考Kirkley 等(2002)的定义，我们可以求得生产环节的生产能力利用率(CUK)，实质为实际产出相对于潜在产出(YP)的生产效率，记为 CUK= Y /YP，因此有1/ CUK= 1/(Y / YP)，从而可以求得Kirkley 产能过剩指数(EXCK，Kirkley Excess Capacity)，E X CK = 1/ CUK- 1 = 1/( Y / YP) - 1，而本文构造的产能利用率(CUA，Actual Capacity Utilization)结合销售市场供大于求的现实特征，将产能利用率分解为生产和销售两个环节，即为：C UA= CUK× SR。

这样，实际的产能过剩指数(EXCA，Actual Excess Capacity)就可以表示为式(6)：

由于 SR ＜1 ，可以判断出：EXCA ＞ EXCK，因此我们计算的产能过剩指数很明显的高于Kirkley 产能过剩指数。

根据式(6)，我们计算得出了2001—2011 年中国工业行业的产能过剩指数，并将结果报告于表2。由表2 我们可以发现，由于生产过程中的技术无效与供大于求(需求不足)双重原因导致的产能过剩现象普遍存在。特别地，由于产能过剩指数大于1(意味着潜在生产能力超过市场实际需求的一倍以上)的行业有15 个，分别为煤炭采选业(S1)、石油和天然气开采业(S2)、黑色金属矿采选业(S3)、有色金属矿采选业(S4)、非金属矿采选业(S5)、纺织业(S10)、服装及其他纤维制品制造(S11)、皮革毛皮羽绒及其制品业(S12)、家具制造业(S14)、文教体育用品制造业(S17)、非金属矿物制品业(S24)、电子及通信设备制造业(S32)、仪器仪表文化办公用机械(S33)、煤气的生产和供应业(S35)、自来水的生产和供应业(S36)。

这一结果明显不同于国内其它研究结果(如韩国高等，2011)，原因在于测算方法的差异。韩国高等(2011)等发现制造业中黑色金属、有色金属、石化炼焦、化学原料、非金属矿物制品、化学纤维和造纸制品七大行业属于产能过剩行业，而我们发现虽然制造业普遍存在产能过剩，但是纺织业(S10)、服装及其他纤维制品制造(S11)、皮革毛皮羽绒及其制品业(S12)、家具制造业(S14)、文教体育用品制造业(S17)、非金属矿物制品业(S24)、电子及通信设备制造业(S32)、仪器仪表文化办公用机械(S33)等行业产能过剩程度较为严重，主要原因为上述行业生产过程中的效率损失严重，若适当调整生产方式，优化生产要素投入结构，随着生产过程中的技术损失的下降与生产效率的提升，上述行业消费市场上的供大于求现象将更为严重。

我们将行业大类的产能过剩指数报告于图2，可以发现高度产能过剩的行业分布在三个行业大类中，电力、燃气和水的生产及供应业产能过剩指数最高，可能的原因在于这个行业的工业企业行政垄断特征明显，可以较为便捷地吸引大量的投资，而且生产环节产能利用率较低(如图1)。采矿业高度产能过剩现象也较为严重，可能的原因在于国家对资源开发产业政策的倾斜，也吸引大量投资，而且生产环节产能利用率也较低(如图1)；制造业仅部分行业高度产能过剩，总体产能过剩现象最低，说明制造业的生产过程的技术效率相对较高，技术损失相对较小。

表2 中国工业36个行业的产能过剩指数(SFA)

图2 中国工业行业大类产能过剩指数走势

特别的，我们将工业整体的产能过剩指数展示于图3，可以发现中国工业行业的产能过剩指数整体趋于下降趋势，这与现实情况有所差异。我们认为，这主要是由于工业生产技术水平的提升(如图4 所示)，生产过程中的效率损失下降，使得生产层面的产能利用率在逐渐提升，这同时意味着生产层面的隐含着的产能过剩在下降，这是导致我们测得产能过剩指数下降的主要原因(因为相比之下消费层面的需求-供给比率变化较小)①按照本文对产能过剩指数的测算方法，需要从生产层面与消费层面来解释中国工业部门整体的产能过剩程度变化情况。由于样本区间内需求供给比率变化相对较小，但生产层面技术水平的提升(如图4 所示)以及生产过程中技术效率损失的下降导致产能利用率提升，是决定产能过剩指数下降的主要原因。作者在此对审稿专家的意见表示感谢。；另一方面，由于市场经济进程持续推进，且随着收入分配不断调整，需求不断上升，消耗掉了大量的过剩产能。我们发现，2004 年是明显的下降拐点，这是由于2003 年后中国再次进入重工业化时代，在消费层面对于原材料等中间投入品产生较高的需求，而且生产技术水平也有所提升。而2008 年产能过剩指数的出现短暂回升，同样也可以从生产与消费两个层面去解释，一方面是由于金融危机造成外部需求降低，而另一方面是由于生产技术效率短暂下降(如图4 所示)。2009 年再次恢复下行趋势，说明金融危机对产能过剩的影响并不持久。但是上述趋势分析仅为经验判断，针对现有产能过剩现象是否仅源于高投资，还将依赖于我们后文的具体分析。

图3 中国工业整体产能过剩指数走势

图4 中国工业整体的生产技术效率水平

三、产能过剩仅仅源于高投资吗？

（一）模型、数据与方法

基于前文对中国工业行业产能过剩指数的测算，本节进一步考察产能过剩现象的影响因素及其影响效果。参考现有研究(韩国高等，2011)，本文考察了投资比重对产能过剩的影响。另外，为了保障分析结果的稳健性，本文添加劳动投入、外资比重、行业竞争强度、研发投入比重等影响因素作为控制变量，各变量及其选取理由与计算方法说明如下。

投资比重(Investment)。考虑到投资是工业企业获得资本投入的主要方式，而且现有研究也支持中国过高的投资导致了产能过剩(韩国高等，2011)，因此本文首先考察投资比重对产能过剩的影响，并采用当年价投资额与工业总产值的比值来衡量。参考陈诗一(2011)的研究，当年价投资额的计算公式为：当年价投资额t=固定资产原值t-固定资产原值t-1。

劳动就业(Labor)。由于劳动是除资本外工业企业的重要生产要素，因此劳动投入水平对工业企业生产能力具有重要影响，这有必要考察劳动投入对产能过剩的影响效果，我们采用工业行业从业人员的对数值来予以刻画。

创新投入(Innovation)。行业创新投入可以决定技术进步的水平，进一步会影响生产能力，从而对产能过剩产生重要影响。本文采用行业科技活动内部支出与工业总产值的比值来予以反映。

外资比重(FDI)。外商直接投资对中国经济做出巨大贡献，这不仅表现在对内资企业的技术溢出从而提升了行业整体的生产能力(张诚等，2001；陈涛涛和陈娇，2006)，更引起内资企业管理制度的变革等。不仅如此，外商直接投资企业还加剧了东道国市场行业内部的竞争程度(Hymer，1976；张杰等，2011)，对东道国市场上的产品需求和供给也具有重要影响。我们采用外资企业总产值与行业总产值的比重予以反映。

行业竞争强度(CI)。测度行业市场竞争程度的指标有很多，比如市场集中度包括贝恩指数、勒纳指数等。勒纳指数测度市场势力，即市场垄断程度，它度量的是价格对边际成本的偏离程度。其计算公式为：

由于工业不同行业价格与边际成本数据难以获取，考虑到数据的可得性与计算的简便性，所以本文参考Cheung 和Pascual(2001)及陈羽等(2007)的研究方法，采用勒纳指数所测度的市场垄断程度对市场势力予以刻画。

其中，LC 为劳动力成本(用工资总额来度量)，Y 为工业总产值；VAI 为工业增加值，其中由于《中国工业经济统计年鉴》中2008 年后不再提供工业增加值的行业数据，按照之前的做法，根据中国统计局公布的历年年末工业分大类行业增加值增长速度与前一年的增加值数据计算得出。

因为勒纳指数值越高，代表行业垄断程度越强，其值越低则意味着行业竞争程度越高，所以我们构造竞争强度指数，计算公式如下：

这样，最后形成的方程如下所示：

式(10)中各解释变量的统计性描述与相关系数分别如表3 和表4 所示。可以看出，各解释变量之间的相关系数均小于0.4，可以忽略多重共线性的问题①本文曾尝试加入出口比重(EXP)变量，发现与控制变量外资比重(FDI)高度相关(相关系数为0.6539)，所以上述变量未作为控制变量进入方程。。上述变量指标数据来自于《中国工业经济统计年鉴》、《中国科技统计年鉴》、《中国劳动统计年鉴》等。考虑到数据可得性与研究的准确性，本文选取2001—2011 年中国36 个工业行业的面板数据作为研究样本②由于自2013 年的《中国工业经济统计年鉴》所提供的2012 的数据较往年变化较大，其中包括工业总产值、行业从业人数等数据不再公布，而且塑料制品业与橡胶制品业也开始合并为一个行业公布数据，为了确保研究结果的准确性，所以本文的研究样本止于2011 年。，由于统计口径不统一的原因，《中国工业经济统计年鉴》中“其他采矿业”、“工艺品及其他制造业”、“废弃资源和废旧材料回收加工业”三个行业的数据没有包含在研究范围之内。

表3 各解释变量的统计描述

表4 各解释变量的相关系数

由于工业行业劳动雇佣量的增加会提升行业产值，在现有情况下这会恶化产能过剩现象，而产能过剩亦将造成行业生产萎靡工人失业等问题(林毅夫等，2010)，二者通常存在双向因果关系。另外，行业竞争强度的增加会诱使工业企业增加产出抢占市场份额，恶化产能过剩现象，而产能过剩又会进一步促使企业加剧恶性竞争(林毅夫等，2010)，二者也存在双向因果关系。因此，式(10)不可避免地存在明显的内生性问题。另外，式(10)隐含地假定了产能过剩指数会随着各个影响因素的变化而发生瞬时变化，即不存在滞后效应。现实情况往往并非如此，由于当期的生产决策往往受到前期的经验影响，而且决策者通常无法准确把握市场供求信息及时调整产量，所以前期的生产过剩情况会对当期产生不可避免的重要影响，即存在所谓的“惯性”。因此，考虑到这种动态延续性与影响结果的滞后性，本文将式(10)扩展为如下动态面板模型形式：

本文采用能够有效控制动态面板数据模型内生性问题的两步系统广义矩估计方法(Blundell 和Bond，1998；Windmeijer，2005)对式(11)其进行参数估计。

（二）结果及讨论

在对模型进行回归之前，我们先采用Arellano-Bond 检验，对方程的干扰项进行序列相关检验，发现所有模型均在1%,的显著水平上存在一阶序列相关(相伴概率小于0.05)，但不存在二阶序列相关(相伴概率也小于0.05)，无法拒绝扰动项无二阶自相关的原假设，而且Sargan 统计量的相伴概率也均超过0.1。上述结果表明，我们选择的滞后期数与所使用的工具变量都是合理有效的。我们将具体结果报告于表5，其中模型1只考虑投资比重与劳动投入两个变量，模型2～4 是依次加入外资比重、行业竞争强度与研发强度的模型。

从回归结果可以明显看出，L.EXCA 的系数显著为正，说明上期的产能过剩比率会明显影响下期，产能过剩存在显著的路径依赖特征，表现出产能过剩的“惯性”。这是由于工业企业决策者在生产活动开始前通常根据上一年度的销售情况对企业本年产量做出预估，包括准备原材料等中间投入品，但是市场供求的变化往往快于决策人进一步决策的时间，因此过剩的情况会出现“惯性”特征。

表5 中Invest 的系数均显著为正，说明投资比重的提升导致了产能过剩的现象，这一结论与现有研究一致(韩国高等，2011；江飞涛等，2012)。改革开放以来，对产业良好前景的社会共识引起投资大量涌入，导致产能过剩的“潮涌现象”十分突出(林毅夫，2007)。尤其是随着新世纪开始，随着工业化、城镇化进程的加快，加之现有的以GDP 增长为核心的政府官员政治晋升体制，使得地方政府具有强烈的动机干预企业投资和利用各种优惠政策招商引资(江飞涛等，2012)，而市场供给与需求的信息不对称，导致较多的行业出现盲目扩张的现象，大量的产品充斥着市场，因此过量的盲目投资是导致产能过剩现象的重要原因之一。

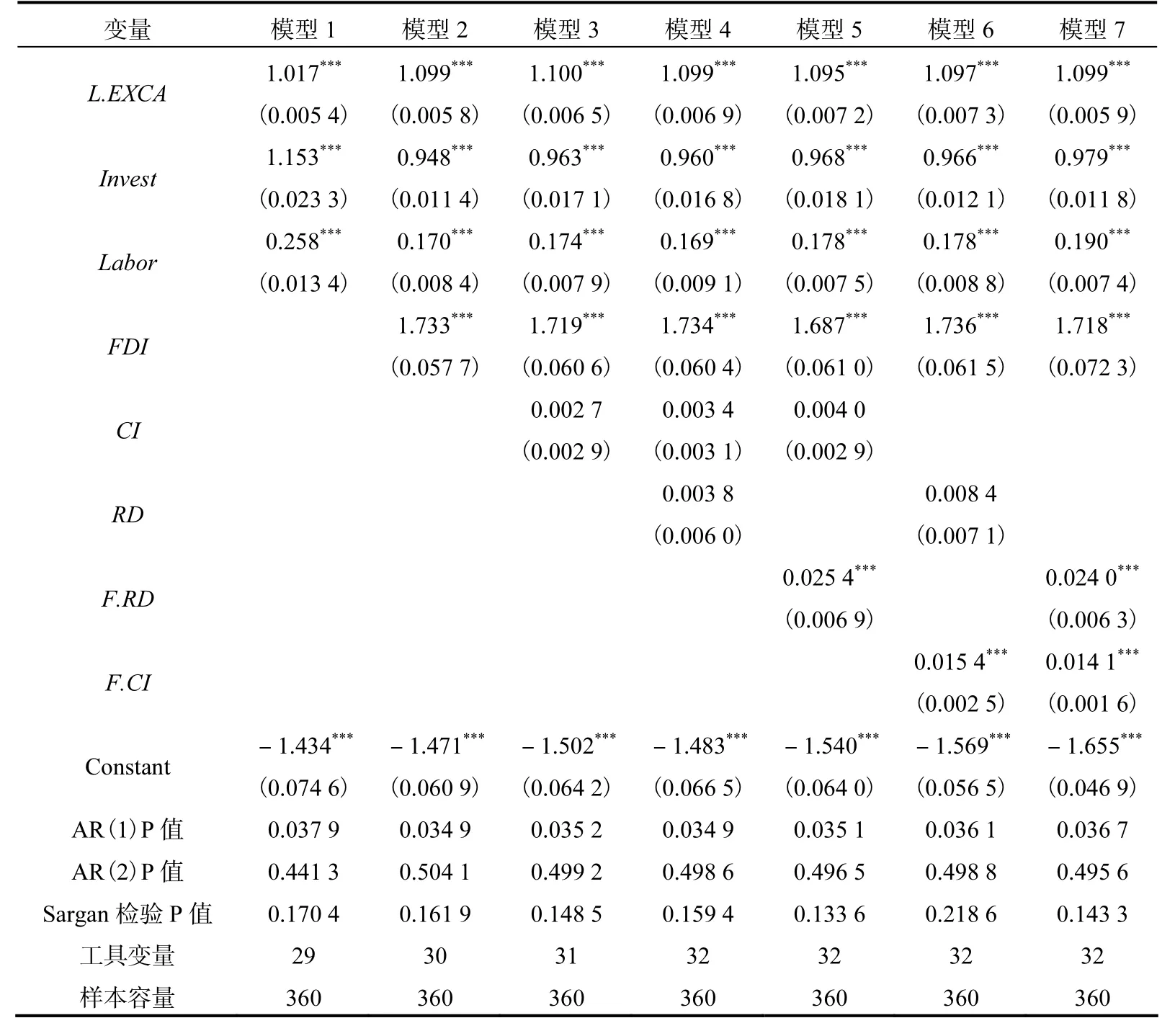
表5 动态面板模型估计结果

表5 中Labor 的系数均显著为正，说明劳动投入的增加也是导致产能过剩的主要原因，这一结论被许多学者所忽略。就业问题一直是各级政府部门关注的重要问题，保持充分就业也是宏观经济发展基本目标之一，劳动就业的下降将会严重威胁国家稳定与宏观经济安全。目前，我国正处于工业化进程加速、第三产业尚未完全崛起的特定发展阶段，工业部门仍然是吸纳就业的关键部门。在当下就业压力较大的背景下，工业行业为解决就业就不可避免的吸收劳动力，这就无法使得生产要素投入结构达到最优的状态，一方面不仅造成生产层面产能利用率较低，另一方面，在现有的生产技术下还会增加消费层面的产品供给。因此，为了维护社会稳定而增加的劳动投入是造成产能过剩的重要原因之一。表5 中模型4 的FDI 的系数也显著为正，说明外资比重的升高也恶化了产能过剩的现象。由于近些年各地政府机关为招商引资开展竞赛，甚至将“吸引外资”纳入考核指标，导致大量外资进入中国。外资企业本身具有较强的生产能力，但是东道国市场上的需求在一定时期内受到消费能力的制约，不仅如此，巨型跨国公司仍然保留着在海外市场上的垄断欲望(江小涓，2002；张杰等，2011)。因此外资进入东道国市场后为获取垄断优势抢占市场份额而增加产品供给，不但对民族企业具有一定的市场挤出效应，也恶化了东道国市场上的产能过剩情况。表5 中模型4 的CI 与RD 的系数虽然为正但并不显著，意味着当期的行业竞争强度与创新投入比重并不是导致产能恶化的主要原因。考虑到创新活动开展到技术水平提升需要经历一定的转化过程(许士春，2007)，可能具有一定的延迟特征，我们将RD 变为其提前1 期F.RD，考察创新投入对产能过剩的滞后影响，并将结果报告于表5 的模型5。此外，行业内部的激烈竞争会促使工业企业改变生产策略，而这也需要一定的时间才可以表现出来，因此我们也考察CI 的提前一期F.CI 对产能过剩的影响效果，将结果报告于模型6。模型7 是同时考察RD 与CI 的提前1 期的影响效果。

通过模型7 可以看出，提前1 期的RD 的系数显著为正，说明创新投入通过滞后效应也恶化了产能过剩情况。创新活动既可以节约生产要素投入降低成本，也可以提升产品质量增加需求。前者提升了生产技术水平与生产层面的产能利用率，但同时也增加了产品供给恶化消费层面的产能过剩，而后者无疑可以缓解产能过剩。因此，创新投入比重的增加对产能过剩的影响效果受两个不同方向的力量制约。从实证分析结果来看，尽管当期影响效果并不显著，但创新投入比重增大的滞后效果恶化了产能过剩程度，说明创新活动提升了技术水平与生产效率对于缓解生产层面的产能过剩作用较为有限。这是由于生产过程中大量的生产要素投入(包括过量投资与劳动力)，在要素节约型技术进步的条件下进一步增加了生产产量与消费市场上的产品供给，不但抵消了效率损失下降引起的生产层面产能利用率上升，而且在供大于求的现有情形下会恶化产能过剩情况①创新活动对产能过剩的影响需要从生产层面与消费层面两个角度去分析，由创新活动引起的生产效率的提升缓解由生产环节造成的产能过剩，但也会增加产出而恶化消费层面的产能过剩，这也解释了为何当期的创新投入比重对产能过剩的影响并不显著，而下期却增加产品供给而恶化产能过剩。作者在此对审稿专家的意见与提示表示感谢。。提前一期的CI 的系数也显著为正，说明行业过度竞争也恶化了产能过剩现象。这是由于行业内部的激烈竞争会促使企业为获取竞争优势增加产量抢占市场份额，这也会导致产能过剩。

四、结论与政策含义

现有研究对于产能过剩测算与影响因素的分析存在不足，本文总结成本法与生产法的优点与缺陷，采用超越对数生产函数的随机前沿模型计算了生产能力利用率与产能过剩指数，之后采用可以有效解决内生性的系统广义矩估计方法考察了投资比重、劳动投入等因素对产能过剩的影响，得出以下结论与政策含义。

第一，中国工业行业由于生产过程中存在效率损失，且销售过程中供大于求，所以导致不同行业均出现不同程度的产能过剩情况。具体而言，采矿业的产能过剩情况最为严重，电力、燃气和水的生产及供应业次之，制造业相对较好。与社会上公认的产能过剩行业不同，本文发现煤炭采选业等15 个行业的产能过剩现象较为严重，意味着如果单纯的提高生产效率降低效率损失，那么供大于求的现象将更为严重。

第二，产能过剩情况存在明显的“惯性”特征，这是由于每个生产年度开始前厂商根据以往经验预估生产投入而又无法及时调整所致。由于新兴市场具有强烈吸引力，加之地方政府为了比拼政绩而干预投资，过量的生产性投资盲目进入而没有考虑市场需求潜力加剧了产能过剩现象。

第三，作为吸纳就业的关键部门，中国工业部门在生产过程中投入了大量的劳动要素，使得生产效率低下而导致实际产出远小于潜在生产能力，这是产能过剩的重要原因之一且往往被忽视。由于各地比拼政绩吸引外资，加之外资企业通常具有先进的生产技术，外资比重的提升会也会加剧产能过剩现象。

第四，由于创新投入效果的延迟性，因此创新投入的提升恶化产能过剩现象的滞后效应较为明显，这是由于现有创新活动以提升生产效率为导向，进一步恶化消费市场上供大于求的现状。而行业内部的激烈竞争产生滞后效应，更使得工业企业为抢占市场份额而增加生产产量，这也会加剧产能过剩现象。

现有研究将产能过剩完全归咎于过量的盲目投资是片面的，为解决就业压力而大量的投入劳动要素会引起生产效率低下，当然也引起了产能过剩。因此应该增加劳动力技能培训，促进产业结构升级优化劳动力要素配置，尤其是通过服务业规模扩张优化劳动力在不同产业部门的配置结构。政府在抑制产能过剩方面应该发挥主导作用，这不仅仅在于出台产业指导目录，合理的引导投资(包括外商直接投资)，更要规范行业竞争秩序，避免恶性竞争。此外，还需指导创新方向，创新方向不仅仅是要素投入的节约，还应该注重产品质量的提升。中央经济工作会议指出积极推进产品质量创新，提升中国产品的海外竞争力，发挥中国经济在全球经济中相对优势，是解决产能过剩重要法宝。新闻、报刊等媒介中的产能过剩并不是真正意义上的产能过剩，产能过剩不仅仅是市场需求小于市场供给这种现象的直观描述，在经济学意义上，产能利用率是现有产出与潜在生产能力的比率，由于技术无效导致的潜在生产能力高于实际产出的现象。在中国工业产品供给大于需求的背景下，考虑生产与需求两个过程的产能过剩要比只考虑生产层面(Kirkley 等，2002)的产能过剩严重更多。因此解决产能过剩需要从生产和需求两个方向共同努力，中央经济工作会议指出“化解产能过剩的根本出路是创新，包括技术创新、产品创新、组织创新、商业模式创新、市场创新”，为化解产能过剩提供了良好的解决思路，若仅仅依赖于生产过程中的技术创新，引起生产效率提高，供过于求的现象将更为严重。因此，着眼于未来，通过产品创新、组织创新、商业模式创新、市场创新以及合理调整收入分配方法等方式提升市场需求潜力将是解决产能过剩问题的根本途径。

［1］ 陈诗一. 中国工业分行业统计数据估算[J]. 经济学(季刊)，2011(4)：735-776.

［2］ 陈涛涛，陈 娇. 行业增长因素与我国FDI 行业内溢出效应[J]. 经济研究，2006(6)：39-47.

［3］ 陈 羽，邝国良. 市场结构与FDI 技术溢出——基于中国制造业动态面板数据的实证研究[J]. 世界经济研究，2011(9)：63-68.

［4］ 干春晖，郑若谷. 中国工业生产绩效：1998—2007——基于细分行业的推广随机前沿生产函数的分析[J]. 财经研究，2009(6)：97-108.

［5］ 高 越，李荣林. 国际生产分割、技术进步与产业结构升级[J]. 世界经济研究，2011(12)：78-85.

［6］ 龚 刚，杨 琳. 我国生产能力利用率的估算[R]. 清华大学中国经济研究中心学术论文，2002.

［7］ 韩国高，高铁梅，王立国，齐鹰飞，王晓妹. 中国制造业产能过剩的测度、波动及成因研究[J]. 经济研究，2011(12)：18-30.

［8］ 何 彬. 基于窖藏行为的产能过剩形成机理及其波动性特征研究[D]. 吉林大学博士研究生论文，2008.

［9］ 江飞涛，耿 强，吕大国，李晓萍. 地区竞争、体制扭曲与产能过剩的形成机理[J]. 中国工业经济，2012(6)：44-56.

［10］ 江小涓. 跨国投资、市场结构与外商投资企业的竞争行为[J]. 经济研究，2002(9)：31-38.

［11］ 林毅夫. 潮涌现象与发展中国家宏观经济理论的重新构建[J]. 经济研究，2007(1)：126-131.

［12］ 林毅夫，巫和懋，邢亦青. “潮涌现象”与产能过剩的形成机制理[J]. 经济研究，2010(10)：4-19.

［13］ 孙 巍，李 何，王文成. 产能利用与固定资产投资关系的面板数据协整研究[J]. 经济管理，2009(3)：38-43.

［14］ 涂正革，肖 耿. 中国的工业生产力革命[J]. 经济研究，2005(3)：4-15.

［15］ 王 兵，於露瑾，杨雨石. 碳排放约束下中国工业行业能源效率的测度与分解[J]. 金融研究，2013(10)：128-141.

［16］ 王维国，袁捷敏. 我国产能利用率的估算模型及其应用[J]. 统计与决策，2012(20)：82-84.

［17］ 许士春. 环境管制与企业竞争力——基于“波特假说”的质疑[J]. 国际贸易问题，2007(5)：78-83.

［18］ 杨 光.中国设备利用率与资本存量的估算[J]. 金融研究，2012(12)：54-66.

［19］ 杨莉莉，邵 帅，曹建华. 长三角城市群工业全要素能源效率变动分解及影响因素：基于随机前沿生产函数的经验研究[J]. 上海财经大学学报，2014(3)：95-102.

［20］ 张 诚，张艳蕾，张健敏. 跨国公司的技术溢出效益及其制约因素[J]. 南开经济研究，2001(3)：3-5.

［21］ 张 杰，周晓艳，郑文平，芦 哲. 要素市场扭曲是否激发了中国企业出口[J]. 世界经济，2011(8)：78-91.

［22］ 钟春平，潘 黎.“产能过剩"的误区——产能利用率及产能过剩的进展、争议及现实判断[J]. 经济学动态，2014(3)：35-46.

［23］ Aigner D.，Lovell C. A. K.，Schmidt P. Formulation and Estimation of Stochastic Frontier Production Function Models[J]. Journal of Econometrics，1977，6(1)：53-66.

［24］ Battes G. E.，Coelli T. J. A Model for Technical in Efficiency Effects in a Stochastic Production Frontier for Panel Data[J]. Empirical Economics，1995，20(2)：325-32.

［25］ Berndt E. R.，Morrison C. J. Capacity Utilizationmeasures：Underlying Economic Theory and an Alternativeapproach[J]. American Economic Review，1981，71(2)：48-52.

［26］ Berndt E. R.，Fuss M. Productivity Measurement with Adjustments for Variations in Capacity Utilization and Other Forms of Temporary Equilibria[J]. Journal of Econometrics，1986，33：7-29.

［27］ Blundell R.，Bond S. Initial Conditions and Moment Restrictions in Dynamic Panel Data Models[J]. Journal of Econometrics，1998，87(1)：115-43.

［28］ Chamberlin E. The Theory of Monopolistic Competition [M]. Cambridge：Harvard University Press，1947.

［29］ Cheung Y. W.，Pascual A. G. Market Structure，Technology Spillovers，and Persistence in Productivity Differentials [R]. CESifo Working Paper，2001，No. 57.

［30］ Dcmsetz H. The Nature of Equilibrium in Monopolistic Competition[J]. Journal of Political Economy，1959，67(1)：21-30.

［31］ Dupont D. P.，Grafton R. Q.，Kirkley J.，SquiresD. Capacity Utilization Measures and Excess Capacity Inmulti-product Privatized Fisheries[J]. Resource and Energy Economics，2002，24：193-210.

［32］ Färe R. The Existence of Plant Capacity [J]. International Economic Review，1984，25：209-13.

［33］ Kamien M. I.，Schwartz N. I. Uncertain Entryand Excess Capacity[J]. American Economic Review，1972，62(5)：918-27.

［34］ Kirkley J.，Paul C. M.，Squires D. Capacity and Capacity Utilization in Common-pool Resource Industries [J]. Environmental and Resource Economics，2002，22：71-97.

［35］ Kirkley J.，Squires D. Measuring Capacity and Capacity Utilization in Fisheries[C]. FAO Fisheries Technical Report No. 386，Food and Agriculture Organization of the United Nations，Rome，1999.

［36］ Klein L. R. Some Theoretical Issues in the Measurement of Capacity[J]. Econometrica，1960，28(2)：272-86.

［37］ Meeusen W.，Broeck J. Efficiency Estimation from Cobb-Douglas Production Functions with Composed Error [J]. International Economic Review，1977，18(2)：435-44.

［38］ Morrison C. J. Primal and Dual Capacity Utilization：An Application to Productivity Measurement in the U. S. Automobile Industry [J]. Journal of Business& Economic Statistics，1985，3(4)：312-24.

［39］ Nelson R. On the Measurement of Capacity Utilization [J]. Journal of Industrial Economics，1989，37(3)：273-86.

［40］ Segerson K.，Squires D. Capacity Utilization under Regulatory Constraints [J]. Review of Economics and Statistics，1992，95(1)：76-85.

［41］ Sahoo B. K.，Tone K. Decomposing Capacity Utilization in Data Envelopment Analysis：An Application to Banks in India [J]. European Journal of Operational Research，2009，195(2)：575-94.

［42］ Windmeijer F. A Finite Sample Correction for the Variance of Linear Efficient Two-step GMM Estimators [J]. Journal of Econometrics，2005，126(1)：25-51.