广东省台风数值模拟与危险性分析
2015-12-25谢汝强,李利孝,王艳华等
广东省台风数值模拟与危险性分析
谢汝强1,李利孝2,王艳华1,方达宪1
(1.安徽新华学院土木与环境工程学院, 安徽 合肥, 230088;2.哈尔滨工业大学深圳研究生院,广东 深圳, 518055)
摘要:广东省是中国沿海最为发达的省份之一,人口密度大,经济总量多,受台风影响严重,每年台风都给这里带来重大经济损失。本文通过对广东省以25公里的距离来划分正方形网格,再以每个网格点为中心,提取台风,并分析各点台风关键参数概率模型。最后利用Monte-Carlo数值模拟方法和Yan Meng风场进行模拟计算,得到各点重现期100年的台风极值风速,并绘出广东省风速分布图,为抗风设计提供参考。
关键词:台风风场;数值模拟;重现期;极值风速度
收稿日期:2014-03-06
基金项目:国家自然科学
作者简介:谢汝强(1976-),男,讲师,硕士,主要从事防灾减灾研究。
DOI:10.11921/j.issn.2095-8382.20150411
中图分类号:X43;P444;TP392
Typhoon Wind Numerical Simulation
and Hazard Analysis For Guangdong Province
XIE Ruqiang1,LI Lixiao2,WANG Yanhua1,FANG Daxian1
(1. College of civil and environmental engineering, Anhui Xinhua University, Hefei Anhui, 230088;
2. Harbin Institute of Technology Shenzhen Graduate School, Shenzhen Guangdong, 518055)
Abstract:Guangdong province is one of the most developed provinces in coastal areas of China. The population density and economic aggregate here are very great. So every year when the typhoon comes, the province is influenced seriously. In this paper, Guangdong province is covered with a nest grid with spacing 25 Km. Using typhoon data of each grid, the probability distributions of key parameters are extracted. Then the extreme wind speeds of 100 years return period are calculated by Monte-Carlo simulation method and Yan Meng wind field model. At last, a new map of wind speeds which can provide a reference for wind-resistant design is proposed.
Key words:Typhoon wind-field models; numerical simulation; return period; extreme wind speed
0引言
台风作为一种自然灾害,每年给中国带来损失都在1000亿人民币之多[1],广东省作为中国经济发展的重要沿海地区,人员伤亡与经济损失首当其冲。根据资料[2],热带风暴登陆中国平均每年7.2个,从进入中国各海区来看,进入南海最多,平均每年14个。广东、海南、福建是台风影响较大的省份,其中广东平均每年有3个台风进入,最多时每年达到7个,是受台风影响最为严重的地区。随着中国经济的飞速发展,沿海一带尤其广东地区,高层与超高层建筑层出不穷,这些建筑对风荷载较为敏感,在结构设计中,风荷载成为主要控制荷载。国内从上世纪90年代对台风开始研究,本世纪初应用于建筑工程。广东作为中国经济最发达且受台风影响最为严重地区,进行台风危险性分析非常有应用价值。当前对台风的研究与应用仅限于个别沿海重点城市地区。2002年欧进萍[3]等应用Batts风场并给合MonteCarlo模拟方法对沿海一些重点城市进行了台风数值模拟。2005年李茜[4]应用Shapiro风场对广州、厦门等地进行数值模拟,并得出重点城市极值风速。2013年王宁娟[5]应用CE风场对深圳、香港等地进行了台风数值模拟。这些模拟结果对沿海重点城市建筑抗风设计提供了有益的参考。台风从海上登陆,登陆点以中小城市及农村居多,并且此处房屋受破坏程度比重点城市更为严重;再者,以城市中心坐标点的极值风速代表本地区的极值风速并不科学。现在的重点城市发展迅速,面积庞大,以点盖面,会错过极值风速,有时结果可能相差较大。因此,本文以广东省为目标,以相距25Km的网格点为研究对象来绘制全省风速图,将会为城市及乡村的房屋抗风设计带来全新的参考。
1台风风场模型
台风风场模型是进行台风数值求解的关键。1980年Batts[6]建立了简单的Batts风场模型。1983年Shapiro[7]在Navier-Stokes公式基础上建立了第二代风场。1995年Vichery[8]对Shapiro风场进行改进,并进行模拟计算,发现结果优于Batts风场。1995年Yan Meng等人[9]建立了考虑边界层摩擦力的压力梯度方程。1996年Thompson[10]对CE风场进行改进,并对台风进行了数值后报,结果较好。国内,1995年佘军[11]等人对CE风场进行改进,建立了适用于海浪后报的风场模型。
2014年,谢汝强[12]利用实测台风Wayne风速与Yan Meng风场、CE风场及Shaprio风场模拟计算风速序列进行对比,发现Yan Meng风场模拟结果与实测数值吻合度较高。
图1台风实测风速与模拟风速
Yan Meng风场数值模型方程如下:
(1)
式中V=Vg+V′;Vg为梯度风速;V′为地表摩擦阻力风速;t为时间;P为气压;f为科氏力系数;F为边界层内摩擦阻力。其中台风气压采用Holland气压模型,其形式如下:
(2)
式中P0为台风中心气压(hPa);ΔP为台风中心气压差(hPa),台风中心气压差由台风外围气压(一般取1010hPa)与台风中心气压之差,大小在0~135之间;Rm为最大风速半径;r为任意点至台风中心距离;B为参数,取值在0.8~1.5之间。
2台风危险性分析与数值模拟
台风危险性分析方法[13]是以某点为模拟点,以250km为半径,提取模拟圆内经过的台风记录资料,对其进行统计分析,得到台风6个关键物理参数(包括年发生率、中心气压差、最大风速半径、移动速度、移动方向和模拟点最小距离等),并分析物理参数的概率模型。根据概率分布用Monte-Carlo模拟方法随机抽样产生台风系列,结合Yan Meng风场进行数值求解,得到台风最大风速序列,据此推算重现期50年及100年的极值风速。
本次分析采用网格法定点,相邻两点之间相距25Km,共有875个网格点覆盖整个广东省。本文采用的台风记录来源于温州台风网(从1949至2013年登陆我国的台风记录有504个,其中206个由广东沿海登陆)。
图2模拟点网格
2.1台风关键参数及其概率模型
台风关键参数概率模型是台风数值模拟的关键所在。应用模拟圆法提取经过各模拟点的台风记录,进行分析数值后,找出关键参数概率模型。台风关键参数备选概率模型见表1。
台风出现频率是由通过250km模拟圆的各年台风发生次数统计得到,泊松分布能较好的表现台风发生次数的概率分布密度。台风移动方向由提取的台风过程中两个前后台风中心点坐标计算而成,顺时针为正,逆时针为负,正北为零。台风数据每6小时采集一次,因此台风移动速度是由前后两个台风中心坐标的计算距离除以时间间隔得到。台风中心气压差是台风中心气压与外围气压之差,一般取外围气压为1010hPa。最大风速半径是台风数据中的一项,直接从数据中提取。模拟点最小距离是指模拟点与台风移动路径间的最小距离,可取模拟点至两相邻台风中心位置连线的垂直距离,以台风移动方向为前方,移动路径在模拟点左侧为正,右侧为负。根据统计数据,其中东经111.274度,北纬20.697度模拟点台风关键参数如图3所示。

表1 台风关键参数概率模型
2.2台风衰减模型
台风登陆后,其强度将会由于地表阻力而逐步衰减,中心气压由于强度减弱而变大,中心气压差而随之变小,直至气旋消失。台风强度衰减变化与地埋位置有关,Vichery[5]在由实测台风数据拟合了台风中心气压差随时间的变化关系:
(3)

(4)
一个台风过程有若干个记录组成,每个记录间隔6个小时。由模拟圆法提取经过模拟点的所有台风记录,从中提取中心气压差,通过拟合便可求解各个系数。部分模拟点衰减系数见表2。表中广州经纬度为东经113.14度,北纬23.08度。
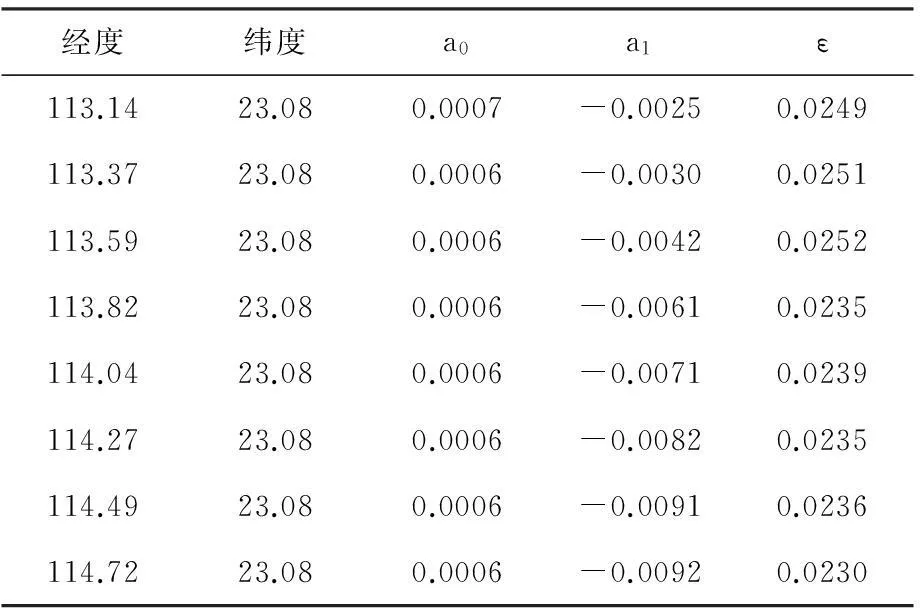
表2 台风衰减系数
2.3台风随机抽样与风速数值模拟
对各个模拟点,由其台风各关键参数概率分布的特征值随机抽样,产生台风起点的各关键参数,再结合台风登陆后的衰减模型,抽取其它系列台风关键参数,直至抽取的台风离开模拟圆为止,即抽取一个台风过程。每个模拟点抽取2500个台风过程,组成一个台风系列。图4中1点为台风起点,由于第7点离开了模拟圆,所以1~6组成一个台风过程。
图4台风模拟过程
利用Yan Meng 风场对每个台风过程进行数值求解,提取在模拟点产生的最大风速,进而把2500个台风过程的最大风速值组成最大风速序列。最后利用台风危险性理论,推算不同重现期的极值风速。
我国极值风速估算常用的方法[14]有极值I型分布及Weibull三参数分布。
极值I型(Gumbel)分布:
(5)
Weibull分布:
(6)
式中,α为尺度参数,β为形状参数,γ为位置参数。
由于我国风速规范采用的是极值I型分布,为了使计算数值统一,重现期100年极值风速采用极值I型分布推算。
最大风速X超越风速XT(重现期为T) 的超越概率为P(X>XT)=1-F(XT),则重现期T=1/[1-F(XT)]。公式(5)经过变形,重现期T下极值风速公式则为
(7)
各网格点重现期100年的极值风速图如图5所示。由等压风速线可以看出,广东省台风风速由沿海向内陆逐渐衰减,其中珠江三角洲一带风速较大,这一带也是高层建筑较为集中的地方,需要重点设防并加强高层建筑抗风研究。另外在广东、湖南与江西交界处,东经113度,北纬25度附近有极大风速区,这一地区处于万时山山峰一侧,地势变化较大,地理位置影响显著。
图5台风等风速线
3结论
Yan Meng风场与其它风场相比,对台风记录的风速求解结果与实测风速吻合度较高。危险性分析方法得到的台风数值模拟结果与重点城市规范风速相比,数值略小,对此结果将进一步分析研究。珠江三角洲地区是广东台风风速较大区域,这与实测台风风速基本相吻合。由于台风衰减模型是与地理位置有关,又由于台风气压模型中有敏感性参数,该参数是动态的,还须对此作进一步探研。
参考文献
1樊运晓, 陈庆寿, 罗云. 区域减灾与可持续发展[J]. 灾害学, 1999, 14(3).
2马艳,张庆华. 关于台风风场研究进展的若干问题探讨[J]. 黄渤海海洋. 1997.17(1):61:64.
3欧进萍, 段忠东, 常亮. 中国东南沿海重点城市台风危险性分析[J]. 自然灾害学报. 2002,11(4).
4李茜, 段忠东. Shapiro台风风场模型及数值模拟[J]. 自然灾害学报. 2005, 14(1):45-52.
5王宁娟.基于 CE 风场数值模拟的台风危险性分析方法研究[D]. 哈尔滨:哈尔滨工业大学,2013.
6Batts M E, Russell L R, Simiu E. Hurricane Wind Speeds in the United States[J]. Journal of Structural. Division.1980, 106(ST10):2003-2005.
7Shapiro L J. The Asymmetric Boundary Layer Flow under Translating Hurricane[J]. Journal of Atmospheric Sciences. 1983, 40(8):1984-1998.
8Vickery P J, Twisdale L A. Wind-field and Filling Models for Hurricane Wind-speed Predictions[J]. Journal of Structural Engineering. 1995, 121(11):1700-1709.
9Yan Meng, Masahiro Matsui, Kazuki Hibi. An Analytical Model for Simulation of the Wind Field in a Typhoon Boundary Layer[J]. Journal of Wind Engineering and Industrial Aerodynamics. 1995, 56:291-310.
10Thompson E F, Cardone V J. Practical Modeling of Hurricane Surface Wind Fields[J]. Journal of Waterways, Port, Costal & Ocean Engineering. 1996, 122(4):195-206.
11佘军, 袁业立, 潘增弟. 一个台风海面风场的数值模式及其后报检验[J]. 海洋学报. 1995, 17(3):24-31.
12谢汝强, 吴韬, 王艳华. 台风风场模型适应性研究[J]. 合肥学院学报(自然科学版). 2014, 24(2): 84-88.
13Russell.L.R. Probability distribution for hurricane effects[J]. Journal of the Waterays, Harbors and Coastal Engineering Division, 1971, 97(WWI):139~154.
14刘聪,秦伟良,江志红.基于广义极值分布的设计基本风速及其置信限计算[J]. 东南大学学报(自然科学版).2006,36(2):331-334.
